隨機部署的無線傳感器網絡的負載平衡

辛強偉，房鼎益

西北大學 信息科學與技術學院，西安 710127

隨機部署的無線傳感器網絡的負載平衡

辛強偉，房鼎益

西北大學 信息科學與技術學院，西安 710127

1 引言

無線傳感器網絡（Wireless Sensor Networks，WSN）的節(jié)點處理能力有限，當數據量較大時，單個節(jié)點或者單一路徑無法承擔負載，因而需要WSN具有良好的負載平衡。在一些實際應用中出現了對少數節(jié)點的過度使用和依賴，而大多數節(jié)點是空閑狀態(tài)，這種狀況容易導致擁塞。此外，節(jié)點自身既感知數據，又要作為路由中繼，由于距離Sink近的節(jié)點轉發(fā)的數據量多于距離Sink遠的節(jié)點，故擁塞較易出現在Sink附近。實現負載平衡有利于WSN減輕網絡擁塞、降低丟包率以及增加網絡生存時間。

關于負載平衡，文獻[1]提出了兩種有效的安排算法以達到負載平衡，設計了相應的協議。文獻[2]提出基于子節(jié)點數目的傳輸調度方法，以確保每個節(jié)點發(fā)送到Sink的數據量相同。文獻[3]中當每個簇不多于兩個簇頭時，提出的方法可以顯著減少最大發(fā)送節(jié)點數目以及平均發(fā)送節(jié)點數目。文獻[4]指出很少的一部分節(jié)點承擔整個WSN的大部分通信量，部分節(jié)點由于鄰居節(jié)點較多而承擔了過大負載。將數據流均衡地劃分給多條鏈路以實現多路徑傳輸是一種實現負載平衡的有效方法。文獻[5]運用多路徑的路由方式，選擇鏈路質量較好的路徑以減少使用鏈路質量不好的路徑。文獻[6]運用多路徑以達到負載均衡，具體方法是根據節(jié)點的能量以不同的概率選擇路徑，從而使能耗均衡。文獻[7]提出了負載平衡樹算法，將數據流均衡地分配給路由樹的不同分支。對于Sink位置的優(yōu)化選擇，需要其附近節(jié)點具備多路徑的分流條件。文獻[8]提出部署多個Sink以分散數據量，從而避免在Sink周圍出現過熱的節(jié)點。本文研究節(jié)點隨機部署這種情況，Sink位置在節(jié)點部署區(qū)域之內或周邊的任意位置。

另外還有一些別的方法：文獻[9]引入幾何法定人數系統來體現內網數據存儲的思想，系統可以較好改善負載平衡并可保持有競爭力的能量效率。文獻[10]把節(jié)點嵌入3維凸多面體，用離散流開發(fā)了一個分布式算法完成嵌入，采用貪婪路由達到負載平衡。文獻[11]指出節(jié)點的部署必須擁有能夠處理最高網絡負載的活動時間。文獻[12]將負載平衡和功率控制結合起來，以使節(jié)點能耗均衡，從而最大化網絡生存時間。文獻[13]建立虛擬骨干網，將連通支配集的大小和負載平衡同時考慮。文獻[14]提出了優(yōu)化分簇來避免簇規(guī)模過大而導致負載不平衡，從而平衡能耗并提升網絡生存時間。文獻[15]在減少總的部署節(jié)點的前提下提出了新的算法以實現負載平衡。上述工作沒有從結構的角度研究在隨機部署節(jié)點時的負載平衡，由于WSN隨機部署的環(huán)境復雜多樣，如山地叢林等野外環(huán)境，繁復的路由算法和復雜的功率控制算法的作用在這樣的環(huán)境下往往得不到有效的發(fā)揮。采用增大節(jié)點密度和統一變化節(jié)點通信半徑這樣的基礎方法反而更易適應WSN隨機部署的復雜多樣的環(huán)境。然而增大節(jié)點密度和統一變化節(jié)點通信半徑對于隨機部署情況下負載平衡的具體影響以及兩者的區(qū)別，尚未得到明確研究。且以往關于負載平衡的研究的前提是已經確定了Sink的位置，而本文的前提是Sink位置不確定，即Sink可位于任意位置。

本文不考慮具體的路由和調度算法，對節(jié)點隨機部署在一區(qū)域內所形成的結構進行統計分析，從結構方面研究負載平衡。這一研究可以為將節(jié)點隨機部署在一區(qū)域內且Sink位置可任意選取的WSN的負載平衡的更為科學的路由和調度算法的設計提供參考。

2 節(jié)點隨機部署的特點分析

2.1 相關符號及定義

N：節(jié)點數目。

R：節(jié)點通信半徑。

k：度，表示鄰居節(jié)點的數目。

S：部署區(qū)域的面積。

d：部署節(jié)點的密度。

L：負載。

定義1（負載）負載L為在時間間隔T內節(jié)點轉發(fā)數據包以及發(fā)送自身數據包的總和。

定義2（同級節(jié)點）到Sink跳數相同的節(jié)點。

定義3（負載平衡）假設WSN的節(jié)點數量為N，每個節(jié)點自身產生的數據量相同，通過多跳的方式傳輸數據，若距Sink某相同跳數的同級節(jié)點有h個，L1，L2，…，Lh表示這h個節(jié)點的負載，負載平衡即L1≈L2≈…≈Lh。

2.2 隨機大規(guī)模部署帶來的均勻化趨勢

假設把部署區(qū)域劃分為m個子區(qū)域，即S=S1+ S2+…+Sm，且每個子區(qū)域的面積都為S/m，因為是隨機部署，每個子區(qū)域在每隨機部署1個節(jié)點時的概率都是相同的，假定概率為P(Xi)，d=N/S，每部署1個節(jié)點都是獨立的，可用一組相互獨立隨機變量 X1，X2，…，XN表示，則當 N→∞，ds1≈ds2≈…≈dsm，這說明隨機大規(guī)模部署會帶來節(jié)點分布的均勻化趨勢。

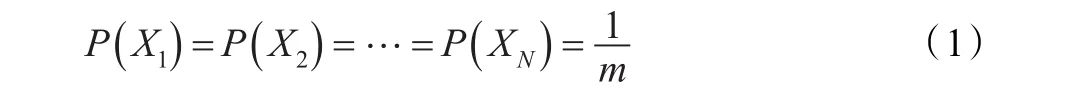
2.3 邊緣效應

由于邊界的存在，靠近邊界和遠離邊界的傳感節(jié)點的覆蓋面積是不同的。以典型的矩形區(qū)域為例，一個節(jié)點覆蓋區(qū)域為πR2。如果是隨機部署在邊緣上的節(jié)點，則其覆蓋區(qū)域為。如果是隨機部署在四個頂點上的節(jié)點，則其覆蓋區(qū)域為。

假定節(jié)點部署的位置距離邊緣的距離為e，若0≤ e＜R，則其覆蓋面積為；若 e≥R ，則其覆蓋面積為πR2。因此節(jié)點的位置距離邊緣的距離在R以內，其鄰居節(jié)點數目以較大概率為節(jié)點的位置距離邊緣的距離在R以外的倍。

因此，隨機部署使得節(jié)點的分布呈現均勻化趨勢，但邊緣效應導致了鄰居節(jié)點數目分布的不均勻。

3 節(jié)點隨機部署情況下的負載平衡

3.1 節(jié)點隨機部署時所具有的規(guī)律

本文采用Matlab模擬在一個500×500的區(qū)域隨機部署節(jié)點。仿真發(fā)現隨機部署傳感節(jié)點在一定區(qū)域里的WSN的鄰居節(jié)點數目的分布近似服從正態(tài)分布。

根據正態(tài)分布曲線的性質，在[μ-σ，μ+σ]區(qū)間的鄰居節(jié)點數有68.25%；在 [μ-2σ，μ+2σ]區(qū)間的鄰居節(jié)點數有85.45%；在 [μ-3σ，μ+3σ]區(qū)間的鄰居節(jié)點數有99.73%；而鄰居節(jié)點數在(μ±3σ)范圍以外的不到0.3%。

假設H0為鄰居節(jié)點數目服從正態(tài)分布；H1為鄰居節(jié)點數目不服從正態(tài)分布。Xj表示實驗中得到的鄰居節(jié)點數目，實驗中得到μ和σ。

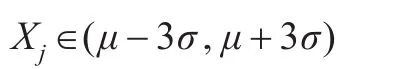
接受假設H0，即大規(guī)模隨機部署傳感節(jié)點在一定區(qū)域里的WSN的鄰居節(jié)點數目的分布近似服從正態(tài)分布。

令 X表示鄰居節(jié)點的數目，正態(tài)分布的密度函數是：

期望為：

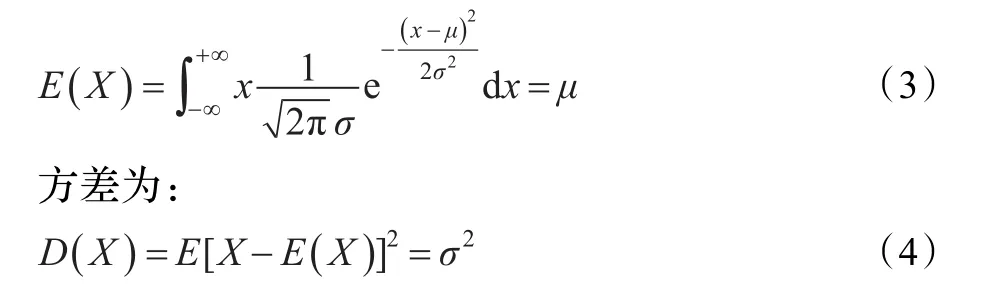
3.2 方差與負載平衡

方差用來度量隨機變量和其數學期望之間的偏離程度。D(X)小，表示集中；D(X)大，表示分散。

性質方差D(X)越小，X的分布就越集中。

證明當D(X)=0，若ε表示任意小，則

根據切比雪夫不等式有：

因此可見方差D(X)越小，X的分布就越集中。

隨著節(jié)點數目的增加和通信距離的增大正態(tài)曲線呈現扁平化趨勢。σ越小表明節(jié)點的鄰居節(jié)點數目集中，σ越大表明節(jié)點的鄰居節(jié)點數目分散。從圖1可見D(X)對正態(tài)曲線的影響：σ越小，正態(tài)曲線越陡峭；σ越大，正態(tài)曲線越扁平。扁平化意味著負載分化越嚴重，正態(tài)曲線越陡峭表示WSN負載較平衡。

通過以上的分析可知減小D(X)可以提高WSN負載平衡。本文用MATLAB仿真來驗證WSN負載平衡問題相關結論。

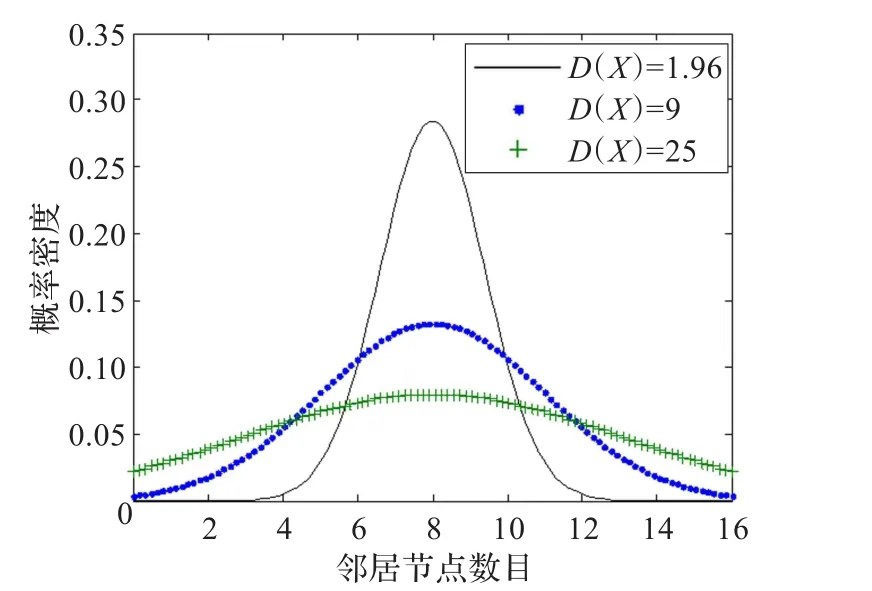
圖1 正態(tài)分布密度曲線比較示意圖

3.3 四種情況的分析

3.3.1 四種情況

本文對4種情況進行了討論，分別是節(jié)點稀疏時小的通信半徑，節(jié)點稀疏時大的通信半徑，節(jié)點稠密時小的通信半徑，節(jié)點稠密時大的通信半徑。節(jié)點稀疏時部署的節(jié)點數為100，節(jié)點通信半徑為25和75。節(jié)點稠密時部署的節(jié)點數為300，節(jié)點通信半徑為25和75。

（1）節(jié)點稀疏，小的通信半徑，如圖2。

（2）節(jié)點稀疏，大的通信半徑，如圖3。

（3）節(jié)點密集，小的通信半徑，如圖4。

（4）節(jié)點密集，大的通信半徑，如圖5。

圖2和圖4顯示網絡中含有鄰居節(jié)點數為0的節(jié)點，表明這時網絡是不連通的。連通是首要問題，連通之后的負載平衡問題才具有意義。鄰居節(jié)點數為0的節(jié)點數目隨著部署節(jié)點的增多或者節(jié)點通信半徑的增大而減少，從而網絡連通狀況得到改善。

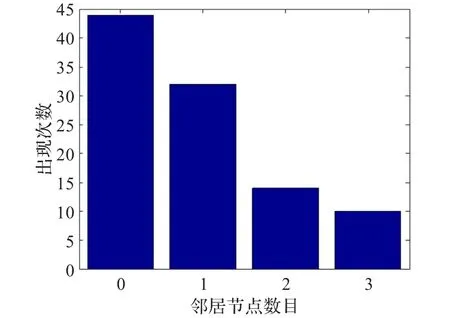
圖2 N=100，R=25

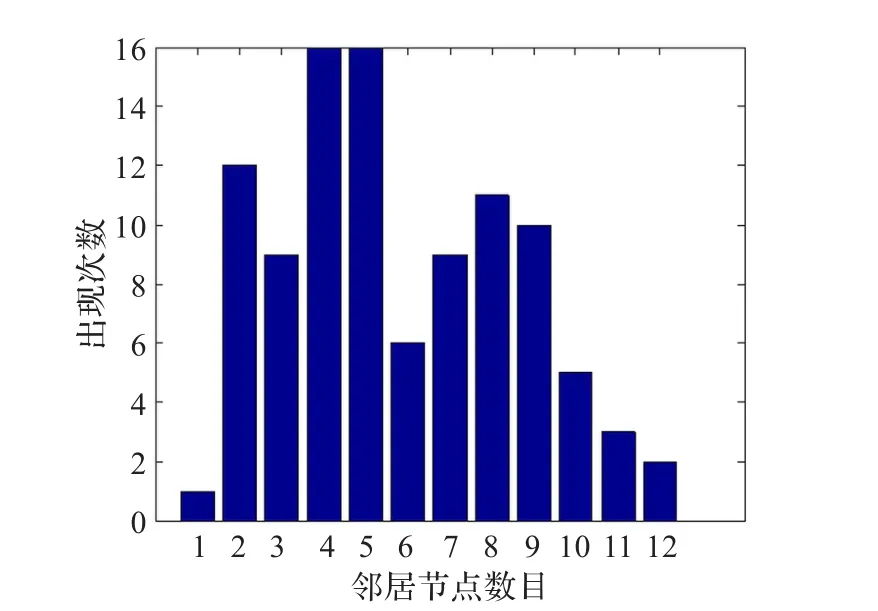
圖3 N=100，R=75

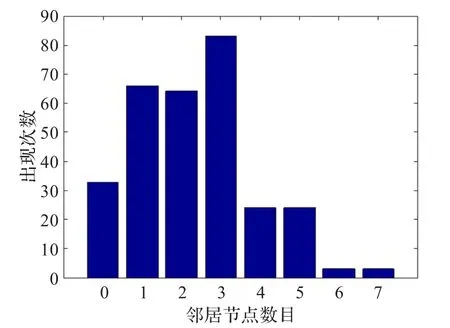
圖4 N=300，R=25

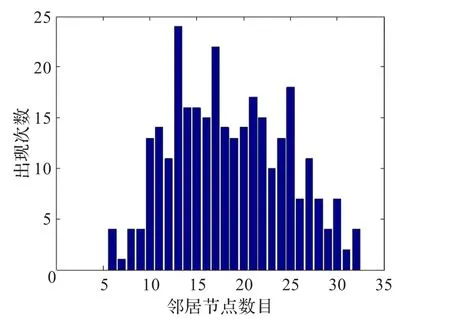
圖5 N=300，R=75

3.3.2 四種情況的比較

圖6～圖9是將圖2～圖5的正態(tài)數據寫入正態(tài)分布密度曲線以進行比較。圖6和圖7是節(jié)點的通信半徑增大至3倍。圖8和圖9是隨機部署節(jié)點的密度增大至3倍。

通過50次實驗，數據是50次實驗的平均值，取至小數點后兩位。

（1）節(jié)點稀疏時通信半徑3倍時的關系：

N=100時，R=75是R=25的E(X)的6.44倍，D(X)的7.67倍。

（2）節(jié)點稠密時通信半徑3倍時的關系：

N=300時，R=75是 R=25的 E(X)的7.96倍，D(X)的16.16倍。

（3）小的通信半徑節(jié)點密度3倍時的關系：

R=25時，N=300是 N=100的 E(X)的2.59倍，D(X)的2.33倍。

（4）大的通信半徑節(jié)點密度3倍時的關系：

R=75時，N=300是 N=100的 E(X)的3.19倍，D(X)的4.92倍。

E(X)的變化：

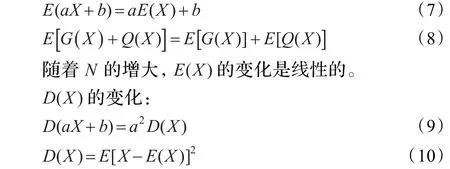
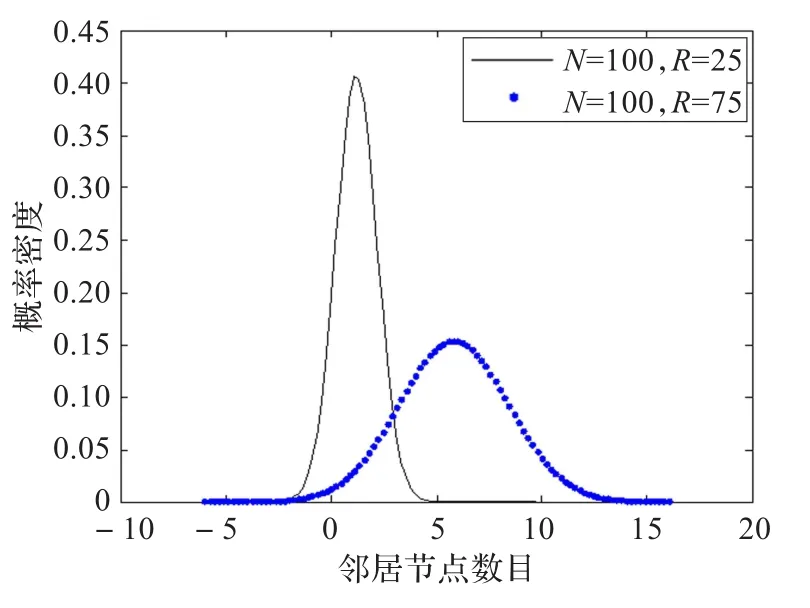
圖6 N=100，R=25和R=75比較

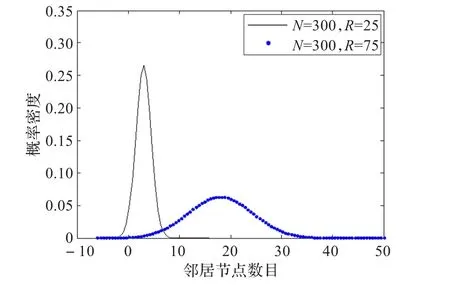
圖7 N=300，R=25和R=75比較

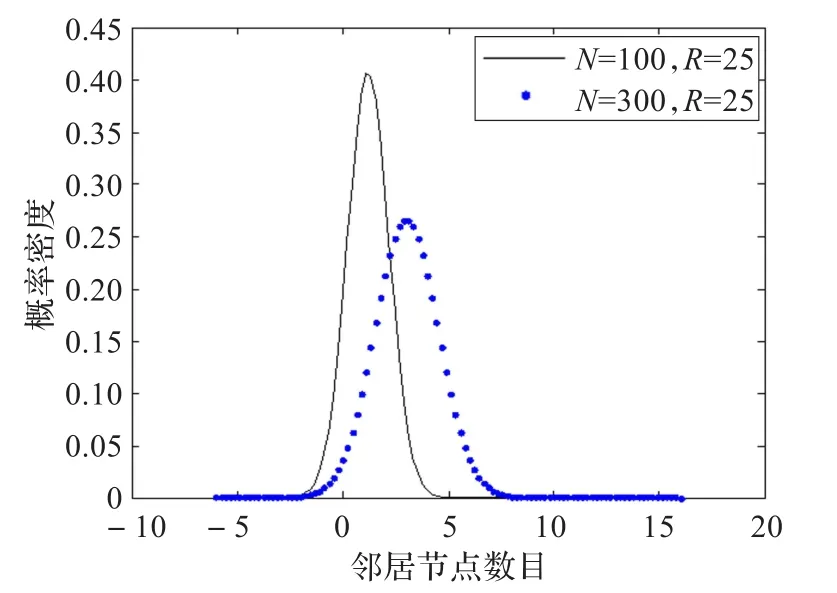
圖8 R=25，N=100和N=300比較

隨著N的增大，D(X)的變化是非線性的。

用Δk來表示WSN中節(jié)點最大度和最小度的差值，即

其中 kmin≥1。

D(X)增大，會使分散程度加重，即會使Δk增大，因而D(X)增大不利于WSN隨機部署情況下的負載平衡。

隨著N增大或者R增大，邊緣效應越明顯，從而使D(X)增大，即鄰居節(jié)點數目的分布隨著節(jié)點數目的增大或者通信半徑的增大而分散程度加重。E(X)的變化是線性的，D(X)的變化是非線性的，當N增大或者R增大時WSN的負載不平衡非線性增大。通過仿真實驗發(fā)現：同樣的倍數關系的增長，節(jié)點通信半徑的增大比節(jié)點數目的增大造成的鄰居節(jié)點數目的分化作用要明顯得多，通信半徑的增大更易造成WSN隨機部署情況下的負載不平衡。

3.4 進一步的討論

從二維平面到三維立體空間的推廣有利于更貼近實際情況。在三維空間V中，節(jié)點的通信范圍是以坐標(x，y，z)為球心、以 R為半徑的圓球。若點 q∈V，設覆蓋度為W，覆蓋度指覆蓋了點q的節(jié)點數目，則在三維空間V中的覆蓋為：

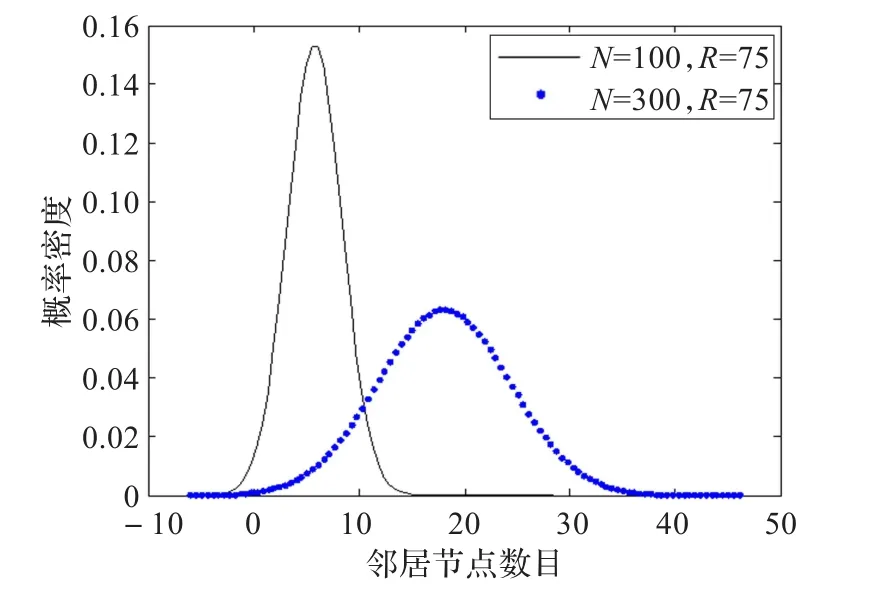
圖9 R=75，N=100和N=300比較

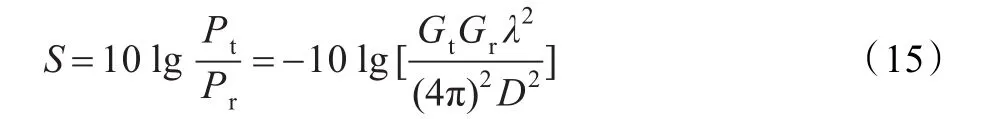
Gt為接收機天線增益，Gr為發(fā)射機天線增益。無線信號在空間傳播中的損耗為：

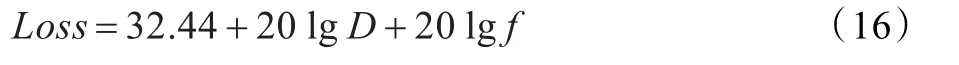
Loss為傳輸損耗，D為距離，f為工作頻率。距離的增大，會使無線信號在空間傳播中的損耗最大，并且RSSI會減小。此外在實際情況中三維立體空間往往存在障礙物的遮擋，比如樹木的遮擋，無線信號在空間傳播中的損耗進一步增大，如果諸如物體遮擋等因素的影響表示為 PL，則

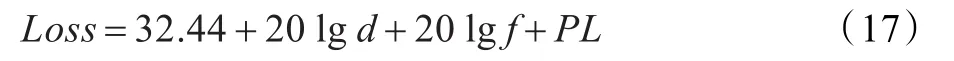
三維空間可以投影到二維平面，假設三維空間中的一點坐標為(ax，ay，az)，若采用正交投影的方法將該點投影到二維平面，假設其在二維平面上的坐標為(bx，by)，則

在WSN的隨機部署中，如山地起伏不平的地形、樹木的遮擋都會引起節(jié)點間通信距離以及無線信號空間傳播損耗的增大。在二維平面上兩節(jié)點的位置分別為(xi，yi)、(xj，yj)，則兩節(jié)點間的距離為：

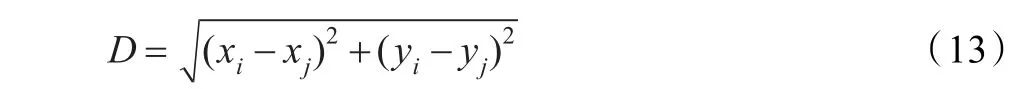
在三維立體空間兩節(jié)點的位置分別為(xi，yi，zi)、(xj，yj，zj)，則兩節(jié)點間的距離為：

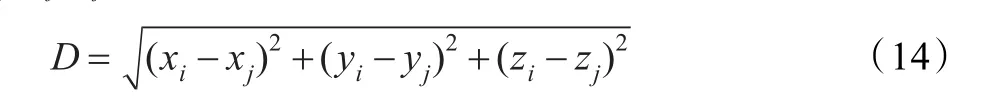
距離的變化影響到了無線信號的傳播，無線信號空間RSSI理論值為：

其中向量t為偏移量，向量u為縮放因子。用矩陣表示為：

因此采用正交投影的方法影響二維平面完全反映三維空間的因素是偏移量和縮放因子，但二維平面還是可以在一定程度上反映三維立體的特點。故對于在二維平面得出的結果，在三維空間可以得到與二維平面類似的結論。

4 結論

本文在不考慮具體的調度和路由算法的情況下，從結構的角度來研究節(jié)點隨機部署且Sink位置任意選取時WSN的負載平衡，以便明晰在隨機部署時所形成的結構對WSN負載平衡的影響。通過分析發(fā)現邊緣效應對隨機部署有著重要影響。仿真發(fā)現隨機部署時鄰居節(jié)點數目近似于正態(tài)分布，且部署密度的增大比節(jié)點通信半徑的增大更有利于隨機部署情況下WSN的負載平衡。

[1]Xiong Shuguang，Li Jianzhong，Li Mo，et al.Multiple task scheduling for low-duty-cycled wireless sensor networks[C]//Proc of IEEE INFOCOM，2011：1323-1331.

[2]Cheng T E，Ruzena B.Congestion control and fairness for many-to-one routing in sensor networks[C]//Proc of ACM SENSYS，2004：148-161.

[3]Zhao Miao，Yang Yuanyuan.A framework for mobile data gathering with load balanced clustering and MIMO uploading[C]//Proc of IEEE INFOCOM，2011：2759-2767.

[4]Liu Yunhao，He Yuan，Li Mo，et al.Does wireless sensor network scale?a measurement study on green orbs[C]// Proc of IEEE INFOCOM，2011：873-881.

[5]Zhou Yangfan，Michael R L.PORT：a price-oriented reliable transport protocol for wireless sensor networks[C]// Proc of IEEE ISSRE，2005：117-126.

[6]Rahul C S，Jan M R.Energy aware routing for low energy ad hoc sensor networks[C]//Proc of IEEE WCNC，2002：350-355.

[7]Chen T S，Tsai H W，Chu C P.Gathering load balaneed treeprotocol for wireless sensor networks[C]//Procof IEEE SENSORNETS，2006：8-13.

[8]Hull B，Jamiwson K，Balakrishnan H.Bandwidth management in wireless sensor networks[C]//Proc of ACM SENSYS，2003：306-307.

[9]Luo Jun，He Ying.GeoQuorum：load balancing and energy efficientdata accessin wirelesssensornetworks[C]// Proc of IEEE INFOCOM，2011：616-620.

[10]Yu Xiaokang，Ban Xiaomeng，Zeng Wei，et al.Spherical representation and polyhedron routing for load balancing in wireless sensor networks[C]//Proc of IEEE INFOCOM，2011：621-625.

[11]Tijs V D，Koen L.An adaptive energy-efficient MAC protocol forwirelesssensornetworks[C]//Proc ofACM SENSYS，2003：171-180.

[12]Rahim K，Riadh D，André-Luc B.Load balancing techniques for lifetime maximizing in wireless sensor networks[J].Ad Hoc Networks，2013，11（8）：2172-2186.

[13]He Jing，Ji Shouling，Pan Yi，et al.Approximation algorithms for load-balanced virtual backbone construction in wireless sensor networks[J].Theoretical Computer Science，2013，507：2-16.

[14]Anju S，Kingsly S R.A secured load balanced clustering algorithm for wireless sensor network[J].International Journal of Research in Computer and Communication Technology，2014，3（4）：517-520.

[15]Chatterjee P，Das N.Coverage constrained non-uniform node deployment in wireless sensor networks for load balancing[C]//Proc of IEEE AIMoC，2014.

XIN Qiangwei,FANG Dingyi

School of Information Science and Technology,Northwest University,Xi’an 710127,China

This paper uses topology to study load balance of wireless sensor networks when sensors are deployed in large scale area randomly.Through the statistical analysis of the number of neighbor nodes of wireless sensor network to study the influence of data flow load balance,the number of neighbor node follows approximately normal distribution when sensors are deployed in large scale area randomly.Its origin lies in the edge effect.Simulation results show that the increase of node communication radius is more difficult to load balance than the increase of deployment density.

wireless sensor networks;load balance;deploy randomly;neighbor node

從結構的角度來研究在大規(guī)模隨機部署時所形成的無線傳感器網絡的數據流負載平衡。通過統計分析鄰居節(jié)點數目來分析其對無線傳感器網絡的數據流負載平衡的影響，發(fā)現在大規(guī)模隨機部署時節(jié)點的鄰居節(jié)點數目近似服從正態(tài)分布，其成因在于邊緣效應。仿真實驗發(fā)現節(jié)點通信半徑的增大比部署密度的增大更不利于負載平衡。

無線傳感器網絡；負載平衡；隨機部署；鄰居節(jié)點

A

TP393

10.3778/j.issn.1002-8331.1404-0272

XIN Qiangwei,FANG Dingyi.Load balance of wireless sensor network with deploying randomly.Computer Engineering and Applications,2014,50（23）：16-20.

國家科技支撐項目（No.2013BAK01B02，No.2013BAK01B05）；國家自然科學基金（No.61070176，No.61202393）；陜西省科技廳國際合作項目（No.2013KW01-02）。

辛強偉（1980—），男，博士研究生，主要研究方向為無線傳感器網絡的容錯和拓撲控制；房鼎益（1959—），男，通訊作者，教授，博士生導師，主要研究領域為無線傳感器網絡、軟件安全和信息安全。E-mail：qiangweifendou@163.com

2014-04-17

2014-06-17

1002-8331（2014）23-0016-05

CNKI網絡優(yōu)先出版：2014-07-01,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1404-0272.html