基于搜索能力均衡的人工蜂群算法

向萬里 ，安美清 ，何瑞春 ，張靜芳 ，馬昌喜

1.蘭州交通大學 交通運輸學院，蘭州 730070

2.天津大學 系統工程研究所，天津 300072

基于搜索能力均衡的人工蜂群算法

向萬里1，2，安美清1，何瑞春1，張靜芳1，馬昌喜1

1.蘭州交通大學 交通運輸學院，蘭州 730070

2.天津大學 系統工程研究所，天津 300072

1 引言

人工蜂群算法（Artificial Bee Colony，ABC）是由土耳其開塞利大學教授Karaboga D于2005年首先提出的一種模仿自然界蜂群集體覓食行為的群體智能優化算法[1]。隨后，Karaboga D與Basturk B將ABC用于約束優化問題的求解[2]，緊接著，Karaboga D與Akay B將ABC與遺傳算法（GA）、粒子群算法（PSO）、差分進化（DE）等元啟發式算法在由近50個函數組成的測試平臺上進行了全面的性能比較，發現ABC總體上優于GA、PSO和DE。加之ABC算法結構簡單、控制參數少、無需梯度信息、易于實現等優點，近來受到越來越多的學者所關注，并已在函數優化[1，3-8]、多目標優化[9]、離散優化[10-12]等領域得到廣泛的應用。

然而，ABC算法各主要階段（雇傭蜂階段、跟隨蜂階段和偵察蜂階段）涉及的解搜索方程更適合于全局探索（Exploration），局部開發能力（Exploitation）欠佳[8]，從而導致ABC的收斂精度和收斂速度還有待進一步提高。為此，眾多學者從各方面進行改進以提高ABC的收斂性能。例如：Akay B和Karaboga D[4]在ABC解搜索方程中引入一個擾動概率參數MR（Modify Rate）用以確定每次進化過程中每個個體會有多少個分量發生擾動，并在此基礎上提出一個自適應尺度因子ASF（Adaptive Scaling Factor）來控制擾動的大小，從而形成一種改進的人工蜂群算法MABC，并取得了不錯的收斂效果；Atalas B[5]則通過引入混沌映射實現種群初始化及在偵察蜂搜索階段利用混沌映射實現混沌搜索，進而提出混沌人工蜂群算法CABC，并且在不同混沌映射作用下作了性能比較分析，指出CABC比ABC取得了更好的收斂精度及更易于跳出局部最優；暴勵、曾建潮等人[6]則使用差分進化（DE）和人工蜂群算法相結合提出了一種新的雙種群差分蜂群算法BDABC，并設計了種群間的學習機制，在仿真實驗過程中BDABC展示了較好的全局搜索性能；Gao W F及Liu S Y[7]采用混沌映射和反向學習理論初始化ABC種群，并在ABC中引入差分變異搜索機制和一個均衡全局搜索和局部利用能力的概率以提高算法的全局收斂性能；此外，Zhu G等[8]基于適應度最好的個體構建解搜索方程，即在ABC解搜索方程的基礎上添加了有最好個體best的引導項，提出了Gbest-guided ABC（GABC），GABC的解搜索方程能有效利用最好個體best的方向引導信息，從而加快ABC的收斂速度和提高收斂精度。在眾多研究的基礎上，本文為進一步提高ABC的收斂性能，提出一種改進的人工蜂群算法（IABC）。首先，為提高ABC的局部開發能力，在ABC的雇傭蜂階段引入了一個新的具有最好個體引導的解搜索方程，從而使得IABC能有效共享利用最好個體信息并指導種群進化；爾后，為均衡ABC的搜索能力，在ABC跟隨蜂階段的搜索策略中引入了新的隨機因素以增強ABC的全局探索能力，使得IABC能有效利用這兩個新的搜索策略來均衡IABC的搜索能力，從而達到提高收斂性能的同時提高收斂精度。最后，在由12個復雜基準測試函數組成的仿真測試平臺上，比較了IABC和ABC及GABC的收斂性能，結果表明IABC的收斂精度和收斂速度都有顯著提高，為進一步驗證IABC的有效性，將IABC與差分進化（DE）及由黃玲玲，劉三陽及高衛峰[13]最近提出的具有人工蜂群搜索策略的差分進化算法（SSDE2）相比較，比較結果亦顯示IABC優勢明顯。

2 改進的人工蜂群算法

2.1 種群初始化

人工蜂群算法通過模擬自然界中蜜蜂的覓食行為實現蜂群個體相互協作，最終實現蜂群采蜜行為涌現的一種群體智能優化算法。因此，在實現人工蜂群算法之初，需要對人工蜂群信息初始化。一般而言，通過式（1）隨機產生SN個雇傭蜂的食物源位置 Xi(Xi=(xi1，xi2，…，xiD))借以表示雇傭蜂個體信息。

其中，i=1，2，…，SN;j=1，2，…，D;xmjin表示第 j個分量所能賦予的最小取值，xmjax表示第 j個分量所能賦予的最大取值，rand(0，1)表示隨機產生[0，1]之間的均勻分布隨機數。

2.2 具有最好個體引導的雇傭蜂策略

對于標準人工蜂群算法，雇傭蜂i在雇傭蜂階段主要是借助式（2）對正在開采的食物源位置進行一次局部開發，并更新食物源位置，以期獲得更好的食物源。

其中 xi，j表示雇傭蜂 i的第 j個分量信息，vi，j表示雇傭蜂i在xi，j基礎上探索或開采出的新食物源位置的第 j個分量位置；k∈[1，2，…，SN]{i}，j∈{1 ，2，…，D} 分別是隨機選擇的雇傭蜂個體及對應的食物源位置的第 j個分量；?ij∈[-1，1]是一個隨機數，用于控制雇傭蜂i進一步搜索的鄰域半徑。

從方程（2）可以看出：原ABC雇傭蜂階段搜索策略中包含3個隨機項：j，k，?ij，使得ABC在搜索過程中具有更多不確定性，ABC從而表現出較好的全局探索（global exploration）能力，而局部開發（local exploitation）能力稍顯不足[8]。為進一步提高ABC的收斂性能，受DE/best/1[14]以及改進的人工蜂群算法GABC[8]的啟示，將ABC搜索方程式（2）修改為具有最好個體引導的式（3）以提高ABC的局部開發能力。

其中，best表示適應度最好的雇傭蜂的索引ID，其余變量含義與式（2）一致。

從式（3）可以看出：新的雇傭蜂搜索策略包含的隨機因素相對式（2）減少了一個隨機索引k的產生，且式（3）有最好的雇傭蜂xbest的引導，使得新的解搜索方程減少不確定因素影響的同時提供了有方向引導的搜索信息，從而強化了ABC的局部開發能力。

2.3 基于適應度尺度變換的選擇概率

為了模仿自然界中的物競天擇，適者生存的自然選擇規律，包括ABC在內的進化算法一般采用如式（4）所示的輪盤賭選擇機制選擇個體，即ABC采用如下方法為跟隨蜂選擇食物源位置提供選擇概率信息pi：

其中，fiti表示適應度，且 fiti由式（5）確定。

其中，f(Xi)表示雇傭蜂i對應的解 Xi的目標函數值，a，b∈R為適應度尺度線性變換參數，當a=1，b=1時，表示適應度計算沒有進行尺度縮放。

經典ABC算法中，跟隨蜂采用式（2）對選擇的雇傭蜂食物源位置進行進一步的開采。考慮到在改進的人工蜂群算法IABC中，雇傭蜂階段食物源的開采采用的搜索方程式（3）具有較強的局部開發能力，為了平衡IABC的搜索能力，以免IABC陷入局部最優而早熟收斂，在式（2）中加入更多隨機因素以使IABC跳出局部最優，提高全局搜索能力，修改后的搜索方程如式（6）所示。

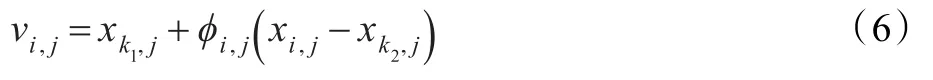
其中，k1≠k2∈[1，2，…，SN]{} i是一隨機整數，j∈[1，2，…，D]是隨機選擇的分量指標。易見式（6）比式（2）多了一項隨機項 xk1，j，從而在式（6）的引導下使得IABC更易于跳出局部最優，能更好地平衡IABC的局部開發和全局探索能力。

2.5 改進的偵察蜂階段

為了進一步均衡改進的人工蜂群算法IABC的局部開發能力和全局探索能力，在此階段，與傳統ABC不一樣，對于每一個雇傭蜂i，均檢測其連續未進化的次數trialsi與控制參數limit的關系，以確定該食物源是否被丟棄，若該雇傭蜂i對應的食物源被丟棄，相應地，雇傭蜂i變成偵察蜂，采用式（1）隨機探索一個食物源位置作為偵察蜂新的食物源，同時偵察蜂變為雇傭蜂，trialsi被置為0。

2.6 IABC算法的基本思想和步驟

Zhu G和Kwong S[8]在GABC中指出傳統人工蜂群算法（ABC）擅長全局探索而局部開發能力不足，即表示ABC在優化過程中存在收斂速度慢的缺點。對此，本文提出一種搜索能力均衡的人工蜂群算法，其基本思想是：首先在ABC的迭代過程中引入最好個體來指導ABC的進化，同時為均衡這種增強的局部開發能力，進而引入一種具有更好全局探索能力的新的跟隨蜂搜索策略，使ABC能有效防止陷入早熟收斂。這兩種新的搜索策略在ABC迭代中循環交替執行，從而使得IABC全局搜索與局部開發能力得以均衡，并使IABC性能大幅提升。具體步驟如下：

步驟1種群隨機初始化。設置循環迭代變量FEs=0；設置最大適應度評估次數maxFEs，控制參數limit以及雇傭蜂個數SN和函數維數D的值；并對所有的trialsi(i=1，2，…，SN)置0。

步驟2SetFEs=FEs+SN。

又三年過去，當她的腳跟上再一次多出一道傷疤，她終于相信這絕不是偶然。她還相信這些傷疤肯定因為秦川。秦川向她隱瞞了太多。

步驟3雇傭蜂階段。

步驟3-1i=0；

步驟3-2i=i+1and FEs=FEs+1，對每一個雇傭蜂對應的食物源位置Xi，根據式（3）產生一個臨時新位置Vi；

步驟3-4 ifi＜SN then轉步驟3-2，否則轉步驟4。

步驟4依據式（4）和式（5）計算選擇概率。

步驟5跟隨蜂階段。

步驟5-1t=0；i=1；

步驟5-2對每一個跟隨蜂，依據概率 pi選擇一個雇傭蜂對應的食物源位置Xi，即

ifrand(0，1)＜pithen 按式（6）產生一個臨時新位置 V andt=t+1and FEs=FEs+1；otherwise，轉步驟5-4；

步驟5-4i=i+1，ifi==(SN+1)theni=1；

步驟 5-5 ift≤SN then 轉步驟 5-2，otherwise，轉步驟6。

步驟6偵察蜂階段。

步驟6-1 fori=1toSN

步驟6-2 iftrialsi＞limitthen

利用式（1）隨機產生一個食物源位置，同時令trialsi=0。

步驟6-3 end for

步驟7記錄到目前為止最好的個體適應度值及其相應信息。

步驟8if FEs≤maxFEsthen轉步驟3，否則，算法終止。

3 仿真實驗

3.1 基準函數及實驗設置

為了驗證IABC算法的有效性，將本文提出的IABC算法與標準ABC及GABC[8]進行了比較。仿真實驗中選擇了廣泛使用的12個具有各種特征的復雜基準測試函數[3，9，7，13]，主要有單模態和多模態及其復雜的移位函數，表1列出了這些函數的名稱、搜索空間及最優值。為了科學比較算法獲得的結果，每個算法均獨立運行20次。仿真實驗過程中，對于GABC涉及的特殊參數C設置為文獻中推薦的值1.5，對于其他共有的參數，為了公平起見，均設置為：群體規模SN=30，函數維數D=30，控制參數limit=100，最大適應度評估次數maxFEs=5E4。此外，對于IABC中的線性適應度尺度變換參數a=100，b=100。

表1 標準測試函數

3.2 仿真實驗性能對比

為了有效對比IABC，ABC及GABC的收斂性能，在Matlab 2009a平臺上對3種算法性能進行仿真測試，各算法分別獨立運行20次，采集20次運行的統計結果：最好值（best），均值（Mean），方差（Std.）。各算法采集的數據如表2所示。

從表2中的數據結果可以看出：對于所有的標準測試函數，IABC獲得的收斂精度和穩定性均勝于ABC和GABC。其中，對于單模態函數 f1、f2及移位單模態函數 f10而言，GABC由于有best個體引導，發現GABC的收斂精度明顯好于ABC，而IABC中best的引導機制是直接在最好個體的選定分量附近探索，不同于GABC中搜索方程的作用是驅動當前個體向best個體靠近，從而使IABC有更強的局部開發能力，表2中的對比結果也顯示IABC對于函數 f1、f2及移位單模態函數 f10的收斂精度明顯好于GABC和ABC；對于復雜多模態函數f3～f9及移位多模態函數 f11，f12而言，GABC大都好于ABC，說明最好個體的指導信息對于算法的收斂性能起了關鍵作用，而IABC好于GABC表明引入IABC的兩個新搜索策略能很好地均衡全局探索和局部開發能力，從而表現出加快收斂速度的同時獲得更好質量的解，尤其是在多模態函數 f3上，IABC獲得了最優值0。

總而言之，從以上性能對比分析可以看出：IABC中對搜索方程的改進起到了加速算法收斂的同時很好地均衡了局部開發和全局探索能力，從而獲得了更好的收斂性能。

為了進一步驗證IABC的收斂性能，將IABC與差分進化算法（DE）以及黃玲玲和劉三陽等[13]最近提出的SSDE2算法的結果進行比較。為公平起見，算法最大的評估次數設置與文獻[13]相同，即100 000。此外，考慮到結果的可靠性，表3中的比較結果除了IABC算法獲得結果值以外，有關DE，SSDE2的結果均直接采用文獻[13]的結果。

表2 3種算法對12個函數的計算結果比較

從表3可以看出：SSDE2和IABC都明顯好于DE。而IABC在除函數 f6以外的9個函數上明顯優于SSDE2，尤其是對于函數 f3，f4及移位多模態函數 f11，f12，IABC均獲得理論極值0，精度遠高于SSDE2，表明IABC具有極好的尋優能力。此外，對于多模態函數 f6而言，SSDE2雖然獲得了比IABC更好的均值和方差，但從表3的注解中可以發現IABC對此函數的20次求解中，有19次獲得了理論極值0，表明IABC有極強的獲取最優值的能力，且這些最好值優于文獻[13]中報道的best值2.22E－016。可以說，表3的對比分析結果再次表明具有搜索能力均衡的人工蜂群算法IABC的收斂性能有較大的改善。

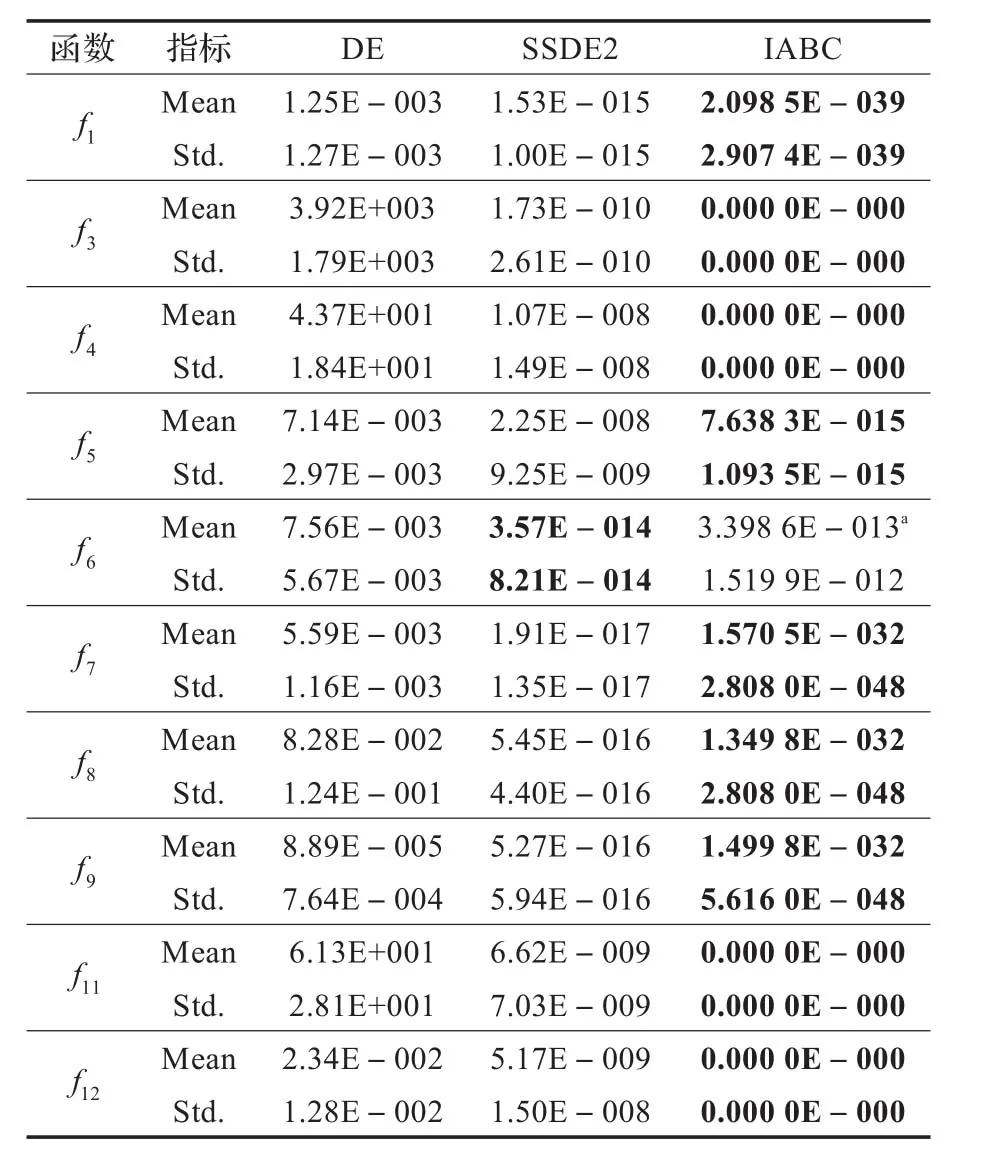
表3 IABC與DE，SSDE2的性能比較

4 結束語

由于標準ABC算法的搜索方程有利于全局搜索，而局部開發能力不足[8]，為進一步提高ABC收斂性能，提出一種改進搜索策略的人工蜂群算法IABC，在改進的IABC中加入了最好雇傭蜂個體best的引導機制，起到向最好個體周圍快速聚集的作用，從而加速算法收斂，提高局部開發能力，同時為了平衡算法的全局探索和局部開發能力，在跟隨蜂階段的解搜索方程中增加了一個隨機項，進而提高IABC的全局探索能力，有利于跳出局部最優，避免IABC早熟收斂。接著，在偵察蜂階段，對于每一個雇傭蜂個體，都檢測其是否變為偵察蜂，再一次使用隨機生成新個體的方式增強IABC后期搜索跳出局部最優的能力，而且在IABC迭代過程中，具有全局探索能力的搜索方程與具有較好局部開發能力的搜索方程交替執行，起到了均衡IABC搜索性能的作用。總之，改進后的IABC在提供局部開發能力的同時，通過在跟隨蜂和偵察蜂階段增加一些隨機策略來均衡IABC的局部開發和全局探索。最后，在由12個常用的復雜基準測試函數組成的測試平臺上進行了仿真測試，發現：本文提出的IABC算法在求解精度、收斂速度及魯棒性方面都比標準的ABC，GABC以及SSDE2均有較大幅度的提高，取得了令人滿意的效果。

[1]Karaboga D.An idea based on honey bee swarm for numerical optimization[R].Kayseri，Turkey：Erciyes University，2005.

[2]Karaboga D，Basturk B.Artificial Bee Colony（ABC） optimization algorithm for solving constrained optimization problems[C]//Proceedings 12th International Fuzzy Systems Association World Congress，2007：789-798.

[3]Karaboga D，Akay B.A comparative study of artificial bee colony algorithm[J].Applied Mathematics and Computation，2009，241（1）：108-132.

[4]Akay B，Karaboga D.A modified artificial bee colony algorithm for real-parameter optimization[J].Information Sciences，2012，192：120-142.

[5]Alatas B.Chaotic bee colony algorithms for global numerical optimization[J].Expert System with Applications，2010，37（8）：5682-5687.

[6]暴勵，曾建潮.一種雙種群差分蜂群算法[J].控制理論與應用，2011，28（2）：266-272.

[7]Gao W F，Liu S Y.A modified artificial bee colony algorithm[J].Computers&Operations Research，2012，39（3）：687-697.

[8]Zhu G，Kwong S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation，2010，217（7）：3166-3173.

[9]Akbari R，Hedayatzadeh R，Ziarati K，et al.A multi-objective artificial bee colony algorithm[J].Swarm and Evolutionary Computation，2012，2：39-52.

[10]Kashan M H，Nahavandi N，Kashan A H.DisABC：a new artificial bee colony algorithm for binary optimization[J]. Applied Soft Computing，2012，12（1）：342-352.

[11]Pan Q K，Fatih Tasgetiren M，Suganthan P N，et al.A discrete artificial bee colony algorithm for the lot-streaming flow shop scheduling problem[J].Information Sciences，2011，181（12）：2455-2468.

[12]Szeto W Y，Wu Y，Ho S C.An artificial bee colony algorithm for the capacitated vehicle routing problem[J].European Journal of Operational Research，2011，215（1）：126-135.

[13]黃玲玲，劉三陽，高衛峰.具有人工蜂群搜索策略的差分進化算法[J].控制與決策，2012，27（11）：1644-1648.

[14]Storn R，Price K.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization，1997，11（4）：341-359.

XIANG Wanli1，2,AN Meiqing1,HE Ruichun1,ZHANG Jingfang1,MA Changxi1

1.School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,China
2.Institute of Systems Engineering,Tianjin University,Tianjin 300072,China

In view of the defect that Artificial Bee Colony（ABC）algorithm is poor at exploitation,an Improved Artificial Bee Colony（IABC）algorithm is proposed based on two new solution search strategies.A new solution search equation, in which the other individual can be driven under the guidance of the best individual with best fitness value,is introduced so as to improve the capability of exploitation.To achieve a good tradeoff between the exploitation and exploration,a new random item is integrated into the original solution search equation to enhance the ability of exploration on the onlooker bee phase of ABC.To further balance the ability of exploration and exploitation,some modifications are done on the scout bee phase of ABC.In order to validate the convergence performance of IABC,experiments tested on twelve benchmark functions are conducted.And the experimental results show that the convergence performance of IABC is enhanced conspicuously.

artificial bee colony algorithm;solution search equation;global exploration;local exploitation;tradeoff

鑒于標準人工蜂群算法（ABC）局部開發能力不足，提出一種改進搜索策略的人工蜂群算法（IABC）。為提高ABC的局部開發能力，在其雇傭蜂階段引入了一個新的具有最好個體引導的解搜索方程，為均衡ABC的搜索能力，在ABC跟隨蜂階段的搜索策略中引入了新的隨機因素以增強ABC的全局探索能力，為了進一步平衡全局探索和局部開發能力，改進了ABC的偵察蜂搜索機制。為驗證IABC的收斂效果，通過在12個復雜基準測試函數上的仿真實驗并與其他算法相比較，發現IABC的收斂性能有顯著提高。

人工蜂群算法；搜索方程；全局探索；局部開發；均衡

A

TP301.6

10.3778/j.issn.1002-8331.1305-0076

XIANG Wanli,AN Meiqing,HE Ruichun,et al.Improved artificial bee colony algorithm based on balance of searching ability.Computer Engineering and Applications,2014,50（23）：51-55.

國家自然科學基金（No.61064012，No.61164003）；蘭州交通大學青年科學基金（No.2012029）；蘭州交通大學科技支撐基金（No.ZC2014010）。

向萬里（1978—），男，博士，副教授，研究領域為進化算法及應用；安美清（1981—），女，講師，研究領域為智能計算及應用；何瑞春（1970—），女，博士，教授，博導，研究領域為人工智能、交通運輸系統優化。E-mail：xiangwl@tju.edu.cn

2013-05-10

2013-06-26

1002-8331（2014）23-0051-05

CNKI網絡優先出版：2013-08-05,http://www.cnki.net/kcms/detail/11.2127.TP.20130805.0943.010.html