單向鏈表快速排序算法＊

白 宇，郭顯娥

（山西大同大學數學與計算機科學學院，山西 大同037009）

1 引言

單向鏈表是一種典型的鏈式存儲結構［1］，目前多使用 Two－way MergeSort算法［2］對單向鏈表進行排序，雖然Two－way MergeSort算法時間復雜度為 O （n log2n）［1～4］，但 其 空 間 復 雜 度 高 達O（n）［1～4］，在一些嵌入式系統研發中，由于對存儲空間的使用數量有較嚴格的限制，故并不普遍適用。

排序算法中適應性最強且應用最廣的是基于關鍵字比較的排序算法［1～4］，因為排序的本質就是按照一定規則相互比較關鍵字以確定其順序，即關鍵字可比較是排序算法的充要條件［3］。而其它諸如基于哈希表的排序算法或基于對關鍵字運算的排序算法，由于對關鍵字有一些特殊要求，其應用相對較窄［4～6］。

在基于關鍵字比較的排序算法中，已證明時間復雜度最小可達O（nlog2n）［4～6］，其中應用最廣泛的有QuickSort和HeapSort，HeapSort算法的常量因子較高［5，6］，QuickSort算法的實測平均性能最優［5，6］。但是，QuickSort算法最大不足之處在于，由于其基于可索引存儲結構設計（一般為數組或索引表），因而無法用于鏈式存儲結構［4］，而鏈式存儲結構的實際應用非常廣泛，例如動態存儲管理、動態優先級調度等等。本文針對上述問題，以QuickSort的分治策略［1～6］為基礎，提出一種可用于單向鏈表的QuickSort算法，其平均時間復雜度（包含最優及最差情況）為O（nlog2n），輔助空間復雜度為O（0），平均遞歸棧空間復雜度為O（log2n），從而實現了對鏈式存儲結構高效排序的同時不增大空間復雜度。

2 算法分析

2.1 分治策略

QuickSort算法需要從線性表兩端逐一選取元素與樞軸元素進行比較［1～6］，而單向鏈表只能從一個方向順序訪問，故無法做到；即使是雙向鏈表，QuickSort算法也要求可以任意交換兩個元素，單向或雙向鏈表也因不能隨機訪問而無法做到。因此，若要對單向鏈表實施分治策略，只能將單向鏈表的首節點作為樞軸節點，然后從單向鏈表首部的第二個節點開始，逐一遍歷所有后續節點，并將這些已遍歷節點的key與樞軸節點的key進行比較，根據比較結果，重新將這些節點鏈接為兩個單向鏈表，其中之一所包含節點的key均小于樞軸節點的key；另一個所包含節點的key均大于或等于樞軸節點的key。這樣，便得到兩個規模更小的單向鏈表，然后對其遞歸執行同樣的操作，并將其分別鏈接到樞軸節點的前部和后部。當在某一層遞歸中，單向鏈表的節點數量小于或等于1時，則為遞歸出口。

為了能在每次劃分后將規模更小的兩個單向鏈表鏈接到樞軸節點上，必須記錄各自的尾節點位置，即需要設置兩個指向尾節點的指針。本文所述算法中將由key小于樞軸節點key構成的單向鏈表定義為less；由key大于或等于樞軸節點key構成的單向鏈表定義為more。這樣，less單向鏈表的首節點指針設定為lessHead，尾節點指針設定為lessTail；more單向鏈表的首節點指針設定為moreHead，尾節點指針設定為moreTail；當前正在遍歷的節點指針設定為current；由于樞軸節點就是未排序的單向鏈表的首節點，故樞軸節點指針設定為listHead。

設節點包含兩個域：key表示用于比較的關鍵字（圖中的k1，k2，…，kn等），next表示指向下一節點的指針（圖中節點的空白區域）。初始化狀態如圖1所示，此時current為listHead的next域。

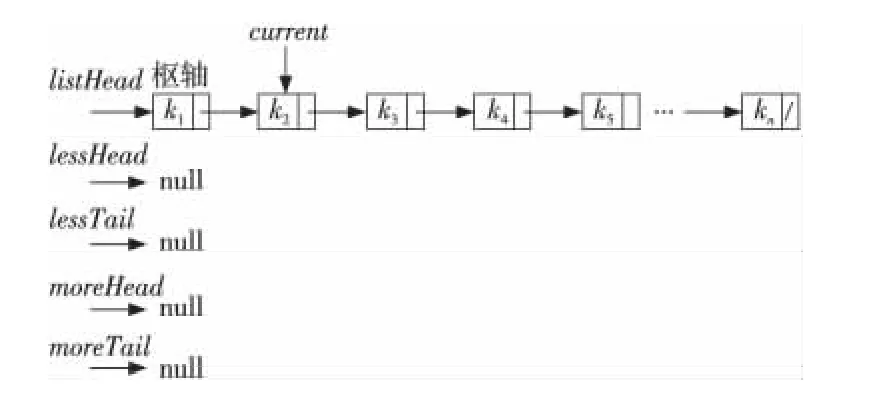
Figure 1 Initializaton state圖1 初始化狀態

當遍歷單向鏈表的兩個節點后，狀態如圖2所示，設k2＜k1，k3≥k1。

Figure 2 State of traversing two nodes圖2 遍歷兩個節點后的狀態

當繼續遍歷單向鏈表的k4和k5節點后，狀態如圖3所示，設k4＜k1，k5≥k1。

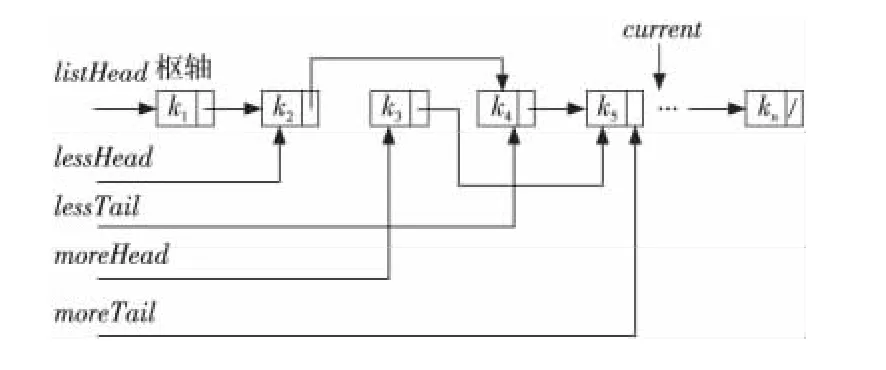
Figure 3 State of traversing four nodes圖3 遍歷四個節點后的狀態

當單向鏈表遍歷結束后，與可索引表的QuickSort算法相類似［1～6］，亦即完成了一趟劃分，如此遞歸進行，便可完成整個單向鏈表的排序。之所以需要設定兩個指向單向鏈表尾節點的指針lessTail和moreTail，一是如前文所述，簡化將less和more單向鏈表鏈接到樞軸節點前、后部的過程；二是簡化向less和more單向鏈表中添加節點的過程，否則需逐一遍歷節點，以尋找該單向鏈表的尾節點，將耗費時間復雜度為O（n）的操作。

2.2 算法正確性分析

算法正確性需要從兩個方面進行分析，其一，當以樞軸節點為中心進行一趟劃分后，樞軸節點前后兩個單向鏈表中節點的key是否相對于樞軸節點有序；其二，遞歸過程是否一定有出口，即遞歸過程是否一定可以在有限步驟后結束。

針對第一個問題，通過遍歷并重新鏈接原單向鏈表為兩個新的子單向鏈表進行解決。在一趟劃分過程中，從樞軸節點listHead的下一個節點開始依次遍歷單向鏈表中的每個節點，如果該節點的key小于樞軸節點listHead的key，則將該節點鏈接到新的子單向鏈表lessHead中；否則將該節點鏈接到新的子單向鏈表moreHead中。當遍歷結束時，所得的子單向鏈表lessHead中的所有節點的key一定小于樞軸節點listHead的key。不失一般性，如圖3，設節點k2＜k1，k4＜k1，則由k2，k4…構成的子單向鏈表lessHead中的所有節點的key均小于樞軸節點listHead的key；同理，由k3，k5…構成的子單向鏈表moreHead中的所有節點的key均大于或等于樞軸節點listHead的key。根據2.1節的描述，此時將樞軸節點listHead鏈接到lessTail后，再將moreHead鏈接到listHead后，不失一般性，如圖3，樞軸節點k1成為兩個子單向鏈表的分割點。因此，以樞軸節點為中心進行一趟劃分后，樞軸節點前后兩個單向鏈表中節點的key相對于樞軸節點是有序的。

針對第二個問題，通過劃分后所形成的兩個子單向鏈表的規模不斷減小，并且當子單向鏈表節點數量小于或等于1時通過終止遞歸調用來解決。一趟劃分后無論劃分結果如何，樞軸節點的位置已經固定，即到達了樞軸節點在排序后所應處于的最終位置上，因此，樞軸節點將不再參與下一輪遞歸調用的劃分過程。因此，在一趟劃分后對兩個子單向鏈表遞歸調用劃分算法時，其規模（節點數量）總是在不斷減小的。當在某一層遞歸調用劃分算法時，如果lessHead等于null，或lessHead等于lessTail，則說明該子單向鏈表中的節點數量小于或等于1，顯然，可以認為該子單向鏈表已經有序，故而可以終止遞歸調用；同理，如果moreHead等于null，或moreHead等于moreTail，同樣可以終止遞歸調用，即此時便是遞歸出口。

通過上述兩個方法，可以保證本文所述算法的正確性。

2.3 算法復雜度

2.3.1 時間復雜度

通過2.1節的分析容易得出，一趟劃分后，樞軸節點對less和more單向鏈表的最優情況是均分（即節點數量之差不大于1）；最差情況是其中之一為空；平均而言，樞軸節點可能出現在1到n的某個位置，顯然包括最優及最差情況。現就三種情況分別分析如下：

第一種情況，每次劃分都將less和more單向鏈表均分，則遞歸棧深度為 log2n＋1，即需遞歸log2n次［7，8］，設需要時間T（n）。第一次劃分需對key做n次比較；第二次劃分，兩個單向鏈表各自需要時間T（n/2）；然后不斷劃分，可得不等式推斷如式（1）：

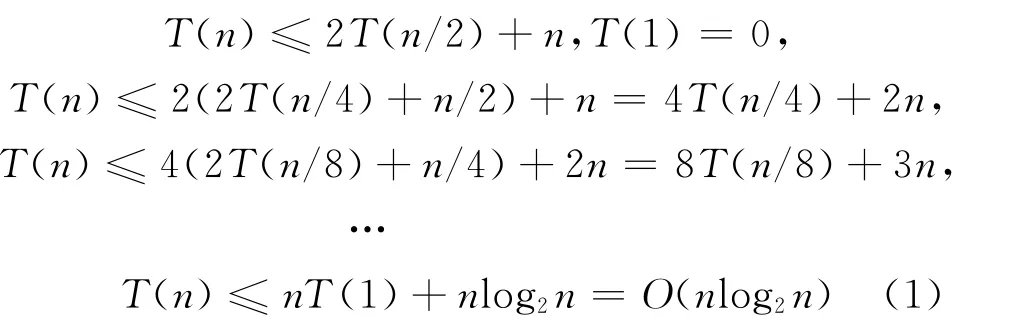
由式（1）可知，本文所述算法在最優情況下的時間復雜度為O（nlog2n）。

第二種情況，每次劃分后，less或more單向鏈表中有且僅有一個為空，則共需進行n－1次劃分，可得：

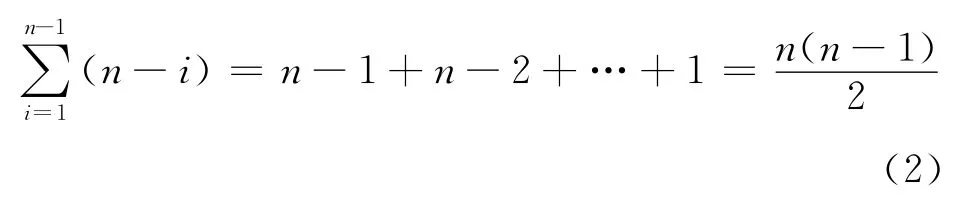
由式（2）可知，本文所述算法在最差情況下的時間復雜度為O（n2）。

第三種情況，平均而言，設樞軸節點在劃分后處于第k個位置（1≤k≤n），可得：

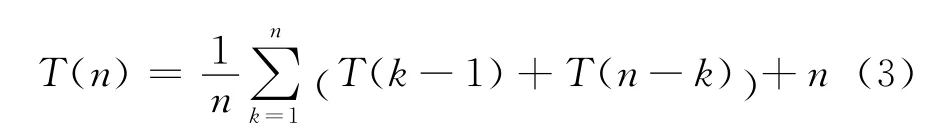
式（3）等價：

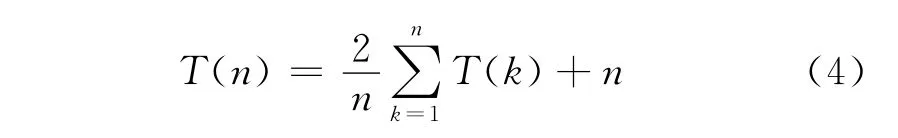
式（4）兩邊同乘n，得：

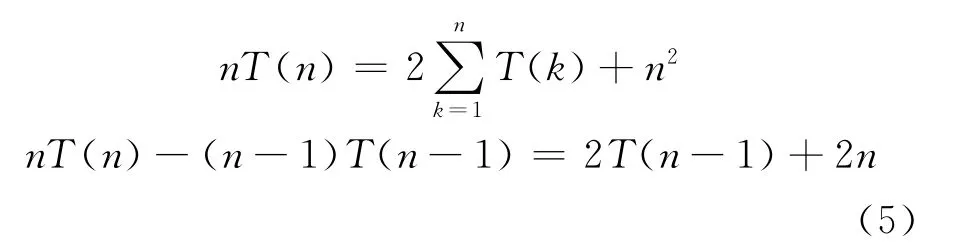
式（5）整理得：

式（6）兩邊同時除以n（n＋1），得：

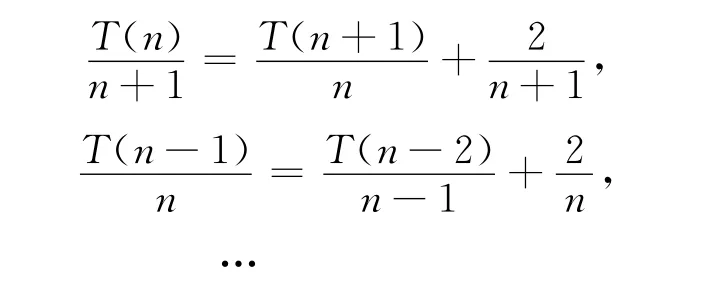
將式（7）中的等式相加，并使用公式：

式（8）中γ≈0.5772，即歐拉常數，可得：

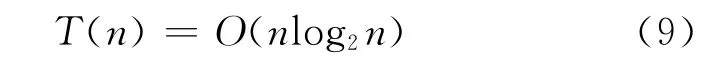
由式（9）可知，本文所述算法在平均情況下（包含最優及最差情況），時間復雜度為O（nlog2n），且遞歸棧平均深度為Θlog2n（Θ為常數）。

2.3.2 空間復雜度

由于本文所述算法采用遞歸結構，因此空間復雜度需從兩個方面進行分析：

（1）用于排序的輔助空間。從2.1節的分析可知，由于算法在排序過程中僅僅重新鏈接原單向鏈表的節點，并不需要任何輔助空間存儲節點。完全不同于針對可索引存儲結構的排序算法，需要輔助空間進行元素交換［1～5］。因此，輔助空間復雜度為O（0）。

（2）遞歸棧空間。從2.3.1節的分析可知，算法的遞歸棧平均深度為Θlog2n（Θ為常數），因此平均遞歸棧空間復雜度為O（log2n）。

3 算法描述

單向鏈表快速排序算法描述如下，具體實現代碼不再贅述：

步驟1 算法接收兩個指針，其中listHead指向單向鏈表首節點，listTail為空指針，劃分過程中，listTail將指向單向鏈表的尾節點，劃分后用于鏈接less單向鏈表到樞軸節點前。

步驟2 如果單向鏈表listHead僅有一個節點，則說明已有序，本層遞歸結束，返回listHead。

步驟3 令lessHead、lessTail、moreHead和moreTail為空，令current為listHead的next域，即單向鏈表的第二個節點。

步驟4 如果current節點為空，則轉入步驟13。

步驟5 如果current節點的key小于樞軸節點（即listHead）的key，則current節點應鏈接到less單向鏈表，轉入步驟6；否則，current節點應鏈接到more單向鏈表，轉入步驟9。

步驟6 修改lessTail指針使其指向current節點。如果lessHead為空，則轉入步驟7；否則轉入步驟8。

步驟7 將current節點鏈接為less單向鏈表的首節點。

步驟8 將current節點鏈接為less單向鏈表的尾節點。

步驟9 修改moreTail指針使其指向current節點。如果moreHead為空，則轉入步驟10；否則轉入步驟11。

步驟10 將currnet節點鏈接為more單向鏈表的首節點。

步驟11 將currnet節點鏈接為more單向鏈表的尾節點。

步驟12 將current節點移動到單向鏈表的下一個節點。

步驟13 如果more單向鏈表不為空，則轉入步驟14；否則轉入步驟18。

步驟14 標記more單向鏈表的結束位置，即置moreTail的next域為空。

步驟15 遞歸調用本算法，繼續劃分more單向鏈表，傳入moreHead和moreTail。

步驟16 將經過遞歸排序的more單向鏈表鏈接到樞軸節點后。

步驟17 修改listTail指針使其指向more－Tail，以便本層遞歸結束后供上層遞歸過程使用。

步驟18 由于more單向鏈表為空，則樞軸節點便是尾節點，即置listHead的next域為空。

步驟19 修改listTail指針使其指向listHead。

步驟20 如果less單向鏈表不為空，則轉入步驟21；否則轉入步驟24。

步驟21 標記less單向鏈表的結束位置，即置lessTail的next域為空。

步驟22 遞歸調用本算法，繼續劃分less單向鏈表，傳入lessHead和lessTail。

步驟23 將經過遞歸排序的less單向鏈表鏈接到樞軸節點前。

步驟24 由于less單向鏈表為空，則樞軸節點便是首節點，即置lessHead為listHead。

步驟25 本層遞歸結束，返回lessHead。

4 實驗測試

4.1 與單向鏈表排序算法實測比較

當前廣泛用于單向鏈表且時間復雜度為O（nlog2n）的排序算法僅有 Two－way MergeSort一種［5］，因此在實驗測試中，選擇該算法作橫向比較，無序數據量分別取25 k、50 k、75 k、100 k和500 k，數據呈均勻隨機分布，范圍為［0，數據量＊2）的正整數［9～12］。使用 C＃2010編譯，在Intel i5 750（2.66 GHz）上運行。取5個不同的隨機數據集，每個數據集測試10次，計算算術平均值，結果如表1所示。

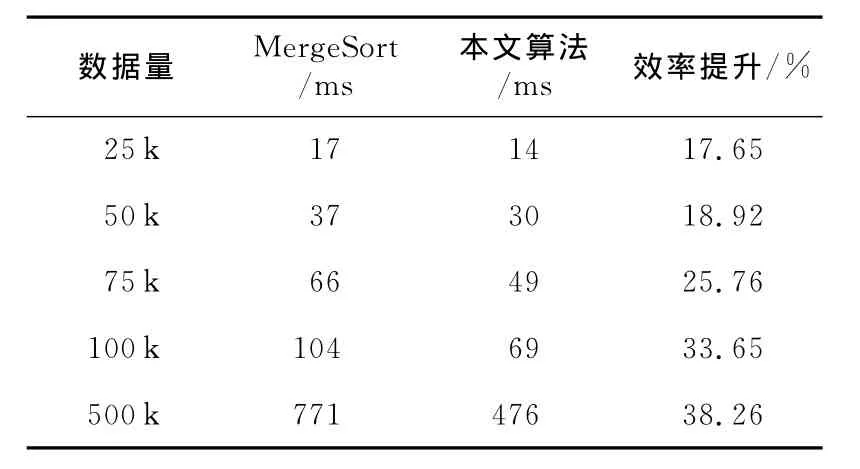
Table 1 Test data 1表1 實測數據一

由表1可知，針對單向鏈表排序，本文所述算法比Two－way MergeSort算法效率平均提升約26.85%。

4.2 與線性表QuickSort算法實測比較

由于線性表QuickSort算法樞軸節點的選取有多種方式［4～6］，為了避免由于樞軸節點選取的不同而導致排序效率的差異［4～6］，需要一致的比較基礎，故本文選擇了使用首節點作為樞軸節點的線性表QuickSort算法作為對比算法，測試數據量、分布、范圍以及測試方法均與4.1節相同，結果如表2所示。

Table 2 Test data 2表2 實測數據二

由表2可知，針對相同數據，本文所述算法比基于線性表的QuickSort算法效率平均提升約11.38%。

5 結束語

綜上所述，本文所述算法的平均時間復雜度（包含最優及最差情況）為O（nlog2n），已達到基于比較的排序算法的時間復雜度的理論極限；其輔助空間復雜度為O（0），即無任何輔助空間開銷；平均遞歸棧空間復雜度為O（log2n），達到了除尾遞歸［7～8，13，14］以外的最小遞歸棧空間復雜 度。因此，本文所述算法的優勢是高效率、低開銷，各項指標較為均衡，是當前時間復雜度等于或接近O（nlog2n）排序算法中為數不多的可應用于單向鏈表的排序算法之一。不足之處是由于單向鏈表不可索引，故劃分算法中不能像基于線性表的QuickSort算法那樣選取中值節點［4～6］作為樞軸節點。根據文獻［5］的實驗結果，基于線性表的QuickSort算法使用中值節點作為樞軸節點后，在均勻和高斯隨機數據分布狀態下，實測有2%～4%的效率提升。

［1］ Joseph B.Data structure programming［M］.New York：Springer Verlag，2005.

［2］ Main M，Savitch W.Data structure and other objects using C＋＋［M］.Boston：Addison－Wesley，2004.

［3］ Kleinberg J，Tardos E.Algorithm design［M］.Boston：Addison－Wesley，2005.

［4］ Thomas H C，Charles E L，Roonald L R，et al.Introduction to algorithms［M］.Massachusetts：Mit Pr，2005.

［5］ Sedgewick R，Wayne K.Algorithms［M］.4th edition.New Jersey：Pearson Education，2012.

［6］ Hagerup T.Algorithm theory—Swat 2004［M］.New York：Springer Verlag，2004.

［7］ Cai Jing－qiu.Note of on recursive program transformation［J］.Microelectronics ＆ Computer，1995，12（6）：45－46.（in Chinese）

［8］ Davies J，Schneider S.Recursion induction for real－time processe［J］.Formal Aspects of Computing.2010，19（2）：119－127.

［9］ Wang Xin－cheng，Sun Hong.Research＆design on high－performance pseudo－random number generator［J］.Computer Engineering and Applications，2004，40（11）：20－23.（in Chinese）

［10］ Qian Hong－bing.The automatic generation of test data［J］.Computer Engineering，1996，22（2）：13－14.（in Chinese）

［11］ Ye Shao－kang，Li Zheng.True random number generator based on mixed－signal circuit［J］.Computer Engineering and Design，2012，33（4）：1602－1606.（in Chinese）

［12］ Ma Xin－sheng，Hu Bin.Research on derivative estimation of periodic random data with hidden periodical model［J］.Journal of Nanchang University（Engineering ＆ Technology），2011，33（2）：200－204.（in Chinese）

［13］ Pitts A M.Structural recursion with locally scoped names［J］.Journal of Functional Programming，2011，21（3）：235－286.

［14］ Jaime A，Bohórquez V.An elementary and unified approach to program correctness［J］.Formal Aspects of Computing，2010，7（9）：38－43.

附中文參考文獻：

［7］ 蔡經球.關于遞歸程序變換的注記［J］.微電子學與計算機，1995，12（6）：45－46.

［9］ 王新成，孫宏.高速偽隨機數發生器的設計與實現［J］.計算機工程與應用，2004，40（11）：20－23.

［10］ 錢紅兵.測試數據的自動生成［J］.計算機工程，1996，22（2）：13－14.

［11］ 葉少康，李崢.基于數模混合的真隨機數發生器［J］.計算機工程與設計，2012，33（4）：1602－1606.

［12］ 馬新生，胡斌.潛周期模型在周期性隨機數據的數值微分中的應用研究［J］.南昌大學學報（工科版），2011，33（2）：200－204.