使用LSA降維的改進ART2神經網絡文本聚類

徐晨凱，高茂庭

上海海事大學 信息工程學院，上海 201306

使用LSA降維的改進ART2神經網絡文本聚類

徐晨凱，高茂庭

上海海事大學 信息工程學院，上海 201306

1 引言

隨著網絡信息的快速增長，每天發布的文本數量呈指數級增長，提供一種有效的文本組織方式顯得日趨重要，而文本聚類可以對文本數據進行較為科學合理的聚類分析和處理，能夠有效地幫助人們去獲取想要的各種信息。

一方面，文本通常采用G.Salton等人提出的向量空間模型[1]（Vector Space Model，VSM）來表示，并通過如TD-IDF算法[2]來提取特征詞的權重，從而形成文本集的矩陣表示。由于文本中出現的單詞眾多，文本特征矩陣往往表現出巨大的維數，從而導致維數災難，文本聚類計算復雜，一些經典統計算法無法適用等。解決這些問題的一種有效辦法就是先對數據進行降維處理。目前，人們已經提出了許多降維方法，如：主成分分析PCA、獨立成分分析ICA、隱含語義分析LSA[3]，其中隱含語義分析LSA根據矩陣奇異值分解理論達到快速降維，是一種較為有效的降維方法。

另一方面，為了對文本數據進行有效的聚類處理，人們已經使用了許多有效的聚類方法，如經典的k-means聚類算法[4]、基于SOM神經網絡[5]的文本聚類算法等。但這些方法往往需要大量的先驗知識來確定聚類簇數目，無法動態學習，對于新向量的學習會影響到已經學習的向量等問題。而根據自適應共振理論提出的ART2神經網絡[6-8]（簡稱ART2網絡）可以有效地動態學習，并且實現記憶和學習的平衡，還能自適應地確定聚類的數目。但ART2網絡依然存在值得改進的地方，如對數據的輸入敏感將會極大影響ART2網絡的聚類結果[9-14]。

針對以上問題，本文提出一種基于最近鄰關系重組數據的改進ART2網絡，在不失動態性的同時，有效地降低了ART2網絡對數據輸入的敏感性，并將LSA理論[3]與這種改進的ART2網絡[7-8]相結合實現文本聚類。先運用LSA理論對文本特征矩陣進行降維處理，再運用改進后的ART2網絡進行文本聚類。實驗表明，該方法不僅能夠快速對文本進行聚類，準確度較高，自動地確定文本聚類簇數目，同時還有效地降低了ART2網絡對樣本輸入順序的敏感性。由于常用的聚類距離有歐氏距離和余弦距離等，而在文本聚類中余弦距離往往比歐氏距離有更好的聚類效果[15]，所以本文所使用的距離是余弦距離，并用距離簡稱。

2 ART2型神經網絡基本原理

2.1 ART2神經網絡模型

本文使用的ART2網絡結構是文獻[8]中使用的網絡結構，如圖1所示。

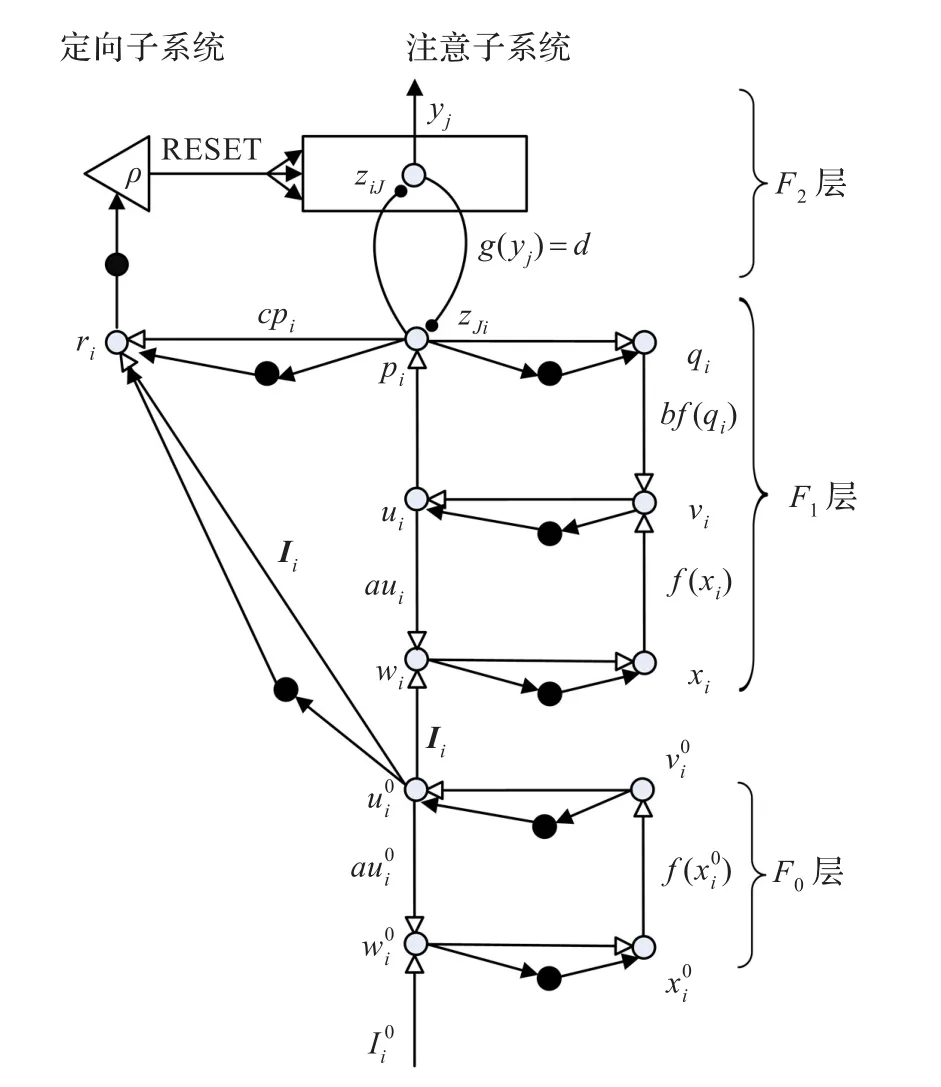
圖1 ART2神經網絡結構

ART2神經網絡一般都由注意子系統[7]（Attentional Subsystem）和定向子系統[7]（Orienting Subsystem）兩大部分組成，而注意子系統又包括F0、F1和F2三層。對于一個未被歸類的輸入信號向量I0，通過F0層的放大增益信號，抑制噪聲，得到處理后的信號I作為F1層和定向子系統的輸入向量。F1層得到F0層的輸入向量之后，將F0層的輸入向量存儲在F1層的STM中，通過非線性變化函數抑制噪聲，放大有用信號，經過多次迭代達到穩定后，將所得向量通過F1→F2的LTM，激活F2層的神經元并得到勝利神經元，勝利神經元通過F2→F1的LTM將反饋信息返回給F1層。F1層得到反饋向量后，再次通過非線性變化函數得到穩定的F1層輸出向量輸出到定向子系統。定向子系統得到F0和F1層的輸出向量后，通過距離計算公式和警戒閾值 ρ，決定是抑制勝利神經元，發出reset信號，重新進行搜索還是讓勝利神經元進入學習階段。

2.2 ART2學習方法討論

對于ART2網絡，傳統的學習方法主要有快速學習方法，慢速學習方法以及折中學習方法。由于在一般常見學習方法中，F2→F1的LTM權值學習方法和對F1→F2的LTM權值學習方法一樣，所以這里只寫出F2→F1的LTM權值的學習方法。

快速學習方法公式[7]如下：

其中，J代表勝利神經元的編號，i代表該神經元LTM的第i個分量，k為學習次數，下同。由式（1）可以得出，勝利神經元學習后的權值完全只與新輸入的輸入信號向量相關，而與之前所學習的輸入信號向量無關。雖然這種方法可以快速使勝利神經元的LTM權值達到收斂，但是也導致該勝利神經元的LTM在一定程度上受到噪聲的影響[8]。

慢速學習方法公式[7]如下：

由式（10）可以得出，慢速學習方法是一個有權重的學習方法，而由于0＜d＜1[7]，所以神經元的LTM更偏向于最近學習的信號向量。又由式（10）可得：

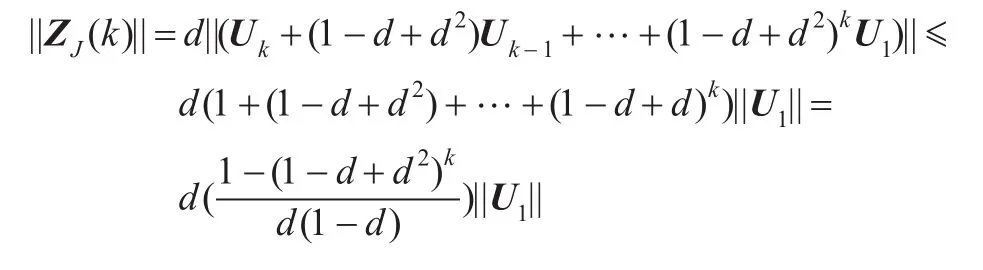
因為U1向量在 F0層已經進行了歸一化操作，所以||U1||的值為1，又因為0＜d＜1[7]，則0＜1-d+d2＜1，隨著k→ +∞，(1-d+d2)k→0，即||ZJ(k)||≤1/(1-d)，由于在F1層凡是小于θ的分量都被去除，而θ≥0，所以往往都有輸入向量距離在0到1之間，則此時有||ZJ(k)||→1/(1-d)。

折中學習方法公式[8]如下：

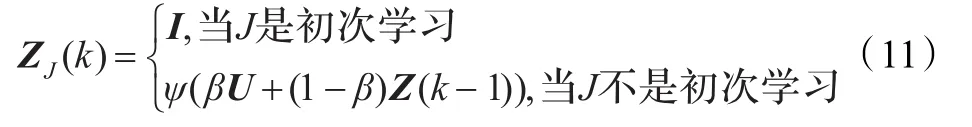
其中ψ為歸一化運算，β為0到1之間的一個參數。

由式（1）（10）（11），可以總結出傳統ART2網絡的學習算法都是非等權重的學習方法。

在許多研究中都使用了一種較為常用的等權重學習方法來減緩向量偏移的問題[10-11]：

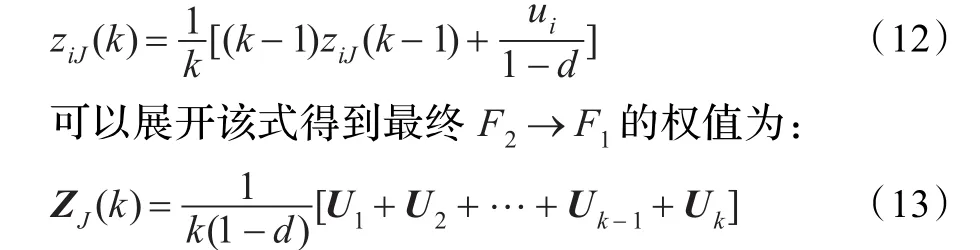
其中k為學習次數。由上述可知||ZJ(k)||＜1/(1-d)，但是顯然||ZJ(k)||的值并非是個定值而是隨著U1，U2，…，Uk之間的夾角變化。該學習方法可以算是一種慢速學習方法，而文獻[8]中的方法要求每次學習完||ZJ(k)||為一個定值，所以無法利用文獻[8]的原理進行步驟上的優化。

本文使用的是一種折中學習方法：

其中，e→0主要防止除0錯誤所以往往取非常小的數值，在計算中可以忽略，WJ(k)為額外的一個向量，由于存放所有歸類在該神經元下的向量和。由式（15）可得，由于e→0，則||WJ(k)||可近似看成是1，為一個恒定值，這就滿足了文獻[8]提出的快速收斂，隨著學習又可以調整的要求。則根據文獻[8]的方法，由于原距離計算函數的主要變量為F2→F1的LTM權值以及兩個向量之間的余弦距離，而由式（15）可得，F2→F1的LTM權值為一個定值，所以可以將原距離計算函數更改為計算余弦距離，又因為在計算勝利神經元時，此時輸入向量U以及F1→F2的LTM權值都是經過歸一化處理之后的向量，所以兩個向量的內積即為其余弦距離，故當第一個勝利神經元未滿足閾值ρ，其余神經元也定無法滿足閾值 ρ，故可直接建立新神經元，從而避免了重新搜索階段，加快了向量的歸類過程并去除了參數c和d[8]，而ART2網絡具體運算步驟與文獻[8]的一致。

3 基于LSA降維方法

隱含語義分析是一種用于知識獲取和展示的計算理論和方法[3]。它主要通過奇異值分解來實現降維，并因此能夠凸顯出文本特征矩陣向量間隱含的語義特征。

設W為m×n的詞條-文本矩陣，其中，m為詞條個數，n為文本個數，則對于矩陣W，可以進行奇異值分解，得到：

其中，U和V矩陣被稱為W的左、右奇異矩陣，Σ為一個對角矩陣，對角線上的每個元素為W的奇異值，并且按遞減順序排列。通過取前r個大的奇異值，并將U與V所對應的r個奇異向量，構建W的r-秩近似矩陣Wr：

其中，Ur矩陣中的行向量對應原矩陣W的r個主要的詞向量，Vr矩陣中的行向量對應原矩陣W的文本向量。

這樣，當使用W 文本矩陣進行聚類時，通過計算WT在Ur矩陣中r個行向量上的投影從而達到降維目的，具體變換方法如下：

其中，W*表示的是降維后的文本-詞條矩陣，W表示原詞條-文本矩陣。

4 基于LSA的ART2神經網絡文本聚類

4.1 ART2神經網絡的不足

由于ART2網絡的神經元LTM的初始權值實際上是由樣本輸入順序決定的，而初始LTM的權值又影響神經元之間的競爭，從而導致ART2網絡的穩定性降低，產生對輸入樣本順序敏感的現象。

設有一組平面上的數據點，類1的數據結點集為{（cos16°，sin16°），（cos20°，sin20°），（cos24°，sin24°），（cos28°，sin28°），（cos32°，sin32°）}，類2的數據結點集為{（cos45°，sin45°），（cos55，sin55°），（cos65°，sin65°），（cos70°，sin70°）}，如圖2所示，采用k-means算法[4]對該數據進行聚類分析可以得到較為理想的聚類結果。

采用ART2網絡進行聚類，由于數據（cos45°，sin45°）和（cos70°，sin70°）的距離為cos25°，若期望ART2網絡分出同樣聚類效果，則需取到合適的ρ使得數據（cos45°，sin45°）和（cos70°，sin70°）能被放入到同一個類簇，通過計算可以得到 ρ至少為cos16°，而數據（cos45°，sin45°）和（cos32°，sin32°）的余弦距離為cos13°，所以無論如何選取 ρ，只要數據（cos45°，sin45°）和（cos70°，sin70°）能歸為同一類簇，那么數據（cos45°，sin45°）和（cos32°，sin32°）也顯然可以通過改變順序歸為同一類簇。若此時數據輸入順序為{（cos45°，sin45°），（cos32°，sin32°），（cos65°，sin65°），（cos55°，sin55°），（cos70°，sin70°），（cos16°，sin16°），（cos20°，sin20°），（cos24°，sin24°），（cos28°，sin28°）}，則會出現當（cos45°，sin45°）輸入時，由于學習的向量為（cos32°，sin32°），則兩者之間的距離滿足閾值ρ，則此時出現如圖3情況。

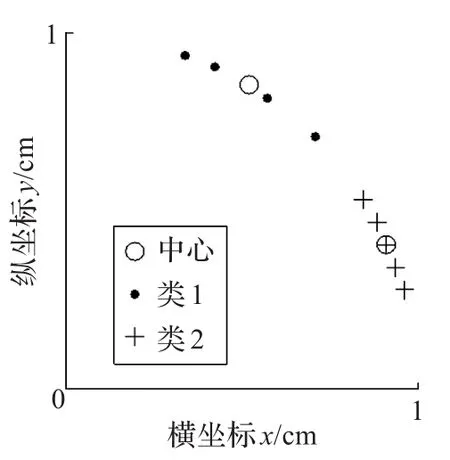
圖2 k-means聚類結果

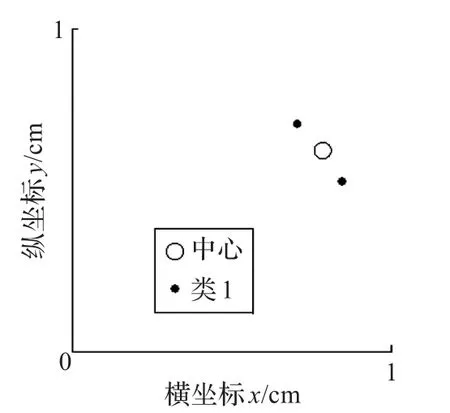
圖3 學習向量（cos32°，sin32°）后

隨后，對向量（cos65°，sin65°）進行聚類，由于其與由（cos45°，sin45°），（cos32°，sin32°）所組成的類的中心向量的余弦距離均不滿足閾值 ρ，所以將在F2層生成一個新的神經元如圖4情況。

之后，（cos55°，sin55°），（cos70°，sin70°）分布在向量（cos65°，sin65°）兩側，且距離類2的神經元更近且其距離值滿足閾值 ρ，則都分別歸類到類2中。最終當所有結果學習完成之后，所得結果最終聚類結果如圖5。根據圖5所示，可以發現，雖然ART2網絡最終獲得的聚類簇個數比預期的要多，但是聚類準確率卻并未提高。而事實上，若原始數據按{（cos45°，sin45°），（cos55°，sin55°），（cos65°，sin65°），（cos70°，sin70°），（cos16°，sin16°），（cos20°，sin20°），（cos24°，sin24°），（cos28°，sin28°），（cos32°，sin32°）}的順序輸入之后，也能得到與k-means聚類結果一致的聚類結果。

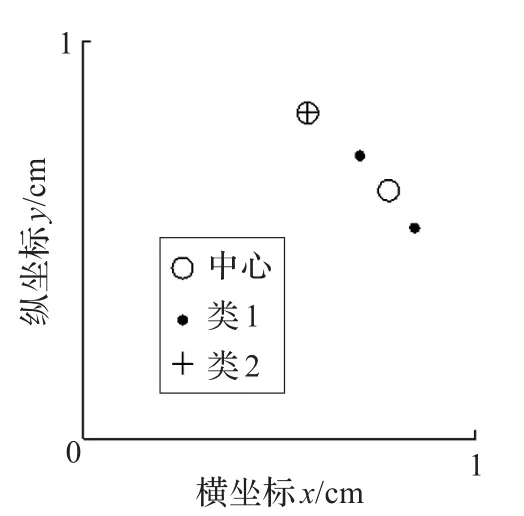
圖4 學習向量（cos65°，sin65°）后

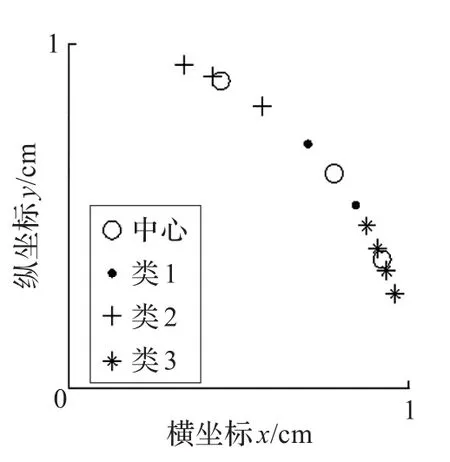
圖5 最終聚類結果

4.2 原因分析

之所以k-means聚類算法具有比ART2網絡有更好的聚類結果，一方面，k-means聚類算法初始中心向量往往是通過一些方法獲取的，而不是簡單的由順序來決定初始中心向量，從而減弱了對數據輸入順序的依賴；而ART2網絡的神經元初始LTM權值從本質上直接依賴于數據的輸入順序，改變數據的輸入順序就可能完全改變了ART2網絡的神經元初始LTM權值，若初始的LTM權值介于類與類之間，從而導致一些不同類的邊緣元素在競爭中以該錯誤的神經元為勝利神經元，又由于是不同類的元素，所以該神經元的LTM權值未必能向某個類的特征方向收斂，從而導致聚類結果不佳。另一方面，k-means聚類算法都是初始中心向量個數固定，由于真實的實際數據當具有一定數量之后，不同類的數據確實有不同特征趨勢的統計特征，從而使得k-means聚類算法的中心向量向某個類的特征方向收斂，通過不斷地迭代，從而使中心向量逐漸收斂從而獲得較好的聚類結果；相反，在ART2網絡中，若恰好原本具有漂移趨勢的中心向量由于新的中心向量產生而被取代，從而使得新的中心向量向某個類的特征中心收斂，而原本的中心向量保持不變，而ART2不會刪除神經元，這樣就導致ART2網絡無論如何迭代，都無法優化聚類結果，同時又增加了聚類類別的個數。

4.3 改進思路

本文根據實體對象往往與其最近鄰實體對象更可能是同一類別這一假設，通過最近鄰關系來動態地調整輸入到ART2網絡中信號向量的所屬神經元，使最終聚類結果更加穩定準確。

4.4 最近鄰重組步驟

本文為ART2網絡額外添加一個最近鄰關系表，其表內每個結點對應一個輸入信號量，其中存放當前所有輸入信號向量之間的最近鄰關系，并且隨著后續信號向量輸入動態維護該表。其主要包含當前結點的最近鄰結點在表中的位置，與該最近鄰的距離值以及一張鏈表，該鏈表主要存放以當前結點為最近鄰的結點所在表中位置信息。而維護過程中需要使用一個棧和一張表來記錄所要處理的結點，該表稱為待處理表，棧稱為遍歷棧。具體步驟如下：

步驟1對新輸入的信號向量，依次計算其與之前的信號向量的距離，若某個舊信號向量的最近鄰距離大于新信號量與該信號量的距離，則將該信號量的最近鄰位置更改為新信號量的位置，其最近鄰值改為與新信號量的距離值，并將該信號量位置信息插入到新信號量的鏈表中。

步驟2通過依次計算之前所有信號向量的距離，將所得到新信號量的最近鄰位置信息及其距離值寫入到新信號向量的結點最近鄰關系表中。

步驟3將新信號向量的結點添加到待處理表中，并將該結點壓入遍歷棧中。

步驟4若棧不空，取出棧頂結點元素，執行步驟6，否則執行步驟5。

步驟5依次遍歷所得結點元素內鏈表中的所有結點，查看鏈表內結點所對應的最近鄰關系表中的結點的最近鄰是否為當前所得結點，若是，則將當前訪問的鏈表元素放入到待處理表中并將其放入棧中，將其所在的ART2網絡對應神經元的LTM權重減去其所對應的信號向量權重，若不是則將其從該鏈表中刪除，直至訪問完鏈表元素后執行步驟4。

步驟6將所得待處理表內結點所對應信號向量權值相加，歸一化后作為新的輸入，輸入到ART2網絡中，將待處理表內結點所對應信號向量歸到最終滿足閾值ρ的獲勝神經元中。

步驟7將新信號向量所對應結點插入到其最近鄰所對應結點的鏈表中，將待處理表清空。

如上例中，當向量（cos65°，sin65°）進入ART2學習之后，雖然此時的情況如之前未修改的ART2網絡結果相同，但是當之后的向量（cos55°，sin55°）進入學習之后，由于向量（cos45°，sin45°）距離（cos55°，sin55°）更近，從而改變了（cos45°，sin45°）的最近鄰，而（cos32°，sin32°）的最近鄰依然是（cos45°，sin45°），所以將（cos32°，sin32°）和（cos45°，sin45°）同時從原神經元中移除，此時該神經元的LTM權值降為0相當于被刪除。而（cos32°，sin32°）和（cos45°，sin45°）與向量（cos55°，sin55°）合并計算出中心向量作為ART2神經網絡的新輸入進行學習，顯然此時網絡只剩下向量（cos65°，sin65°）所在的神經元，并且其距離滿足閾值 ρ。雖然此時，向量（cos32°，sin32°）被誤分，但是隨著后續向量的進一步學習，當向量（cos28°，sin28°）進入時，由于此時（cos32°，sin32°）的最近鄰變成（cos28°，sin28°），從而在原神經元中被移除，而（cos45°，sin45°）的最近鄰依然保持不變，故只有（cos32°，sin32°）和（cos28°，sin28°）合并成為新的輸入，輸入到ART2網絡中，并最終歸到正確的神經元中，經過改進后的ART2網絡所得聚類結果與k-means結果一致，比起未改進的ART2網絡所得聚類結果更加正確及穩定。

4.5 基于LSA的改進ART2神經網絡文本聚類步驟

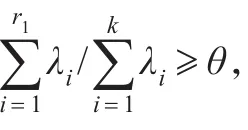
步驟1將所要聚類的文本向量通過投影矩陣，投影到降維后的向量空間中。

步驟2將所得投影后的降維向量輸入到改進后的ART2神經網絡中，進行歸類與學習。

步驟3將在同一個輸出神經元上獲勝的所有輸入文本向量歸為一類，并將此結果作為最終聚類結果輸出。

4.6 算法復雜度分析

在預處理過程中，將會使用LSA來獲取用來投影的投影矩陣，其中SVD分解需要花費一定時間，但SVD算法已經較為成熟，一般需要O(n3)的時間復雜度，但由于該操作只在預處理過程中進行，所以只需要一次獲取投影矩陣即可，故時間開銷可忽略。

在ART2神經網絡聚類過程中，由于先要維護最近鄰表，所以需要O(n)的計算時間，之后需要抽取出相應的最近鄰關系，這里使用鄰接表數據結構進行優化，將最近鄰表變成了最近鄰樹從而只需要沿指針遍歷即可，所以問題即為遍歷一棵樹，其時間復雜度為O(n)，而對于一個新輸入的信號向量，由于本文無需重新搜索，大大加快了聚類速度，故只需要常數步定可將一個信號向量歸類到一個神經元中，而計算勝利神經元的時間復雜度至多為n次，所以最終復雜度為O(n)，而上述每個步驟都是順序執行，所以對于一組n個文本向量的聚類時間復雜度為O(n2)。

在空間復雜度上，由于使用了鄰接表來優化時間并且保存最近鄰關系，所以其空間復雜度為O(n2)，而由于最近鄰重組時需要使用之前輸入的信號向量，所以需要保存之前的信號向量，其復雜度為O(nm)。

5 實驗分析

為了驗證本文提出的改進算法對于文本聚類的有效性以及對順序敏感性的減弱，設計了3組對照實驗，實驗文本采用海量公司中文智能分詞產品[17]進行預處理，共5類486篇。實驗1中數據按類順序輸入，實驗2改變了樣本的輸入順序，按隨機順序。實驗3將文本數據分兩次輸入，第一次輸入先抽取出286篇文本，并通過LSA計算得到投影矩陣，降維并進行聚類，之后將剩余200篇通過之前得到的投影矩陣降維后，作為第二次輸入進行聚類。實驗1主要驗證本文算法能夠準確有效地進行聚類分析，通過LSA降維之后，能夠凸顯出語義關系，減少噪聲，突出最近鄰關系的準確性，從而能夠提高聚類結果的準確性；實驗2驗證本文算法能夠有效地減弱聚類結果對樣本輸入順序的敏感；實驗3驗證各聚類算法的動態性。

為了衡量算法最終所得聚類結果的準確性，本文采用準確度衡量方法，該方法較為直觀，比較容易理解，計算方法如下：

p=聚類簇正確數據點數/實際該類數據點總數

本文采用基于余弦距離的k-means算法[4]、ART2網絡[8]與本文改進算法進行對比，所得實驗結果如表1所示。本文所使用的ART2網絡的參數設置[12]為a=100，b=100，θ=0.001。

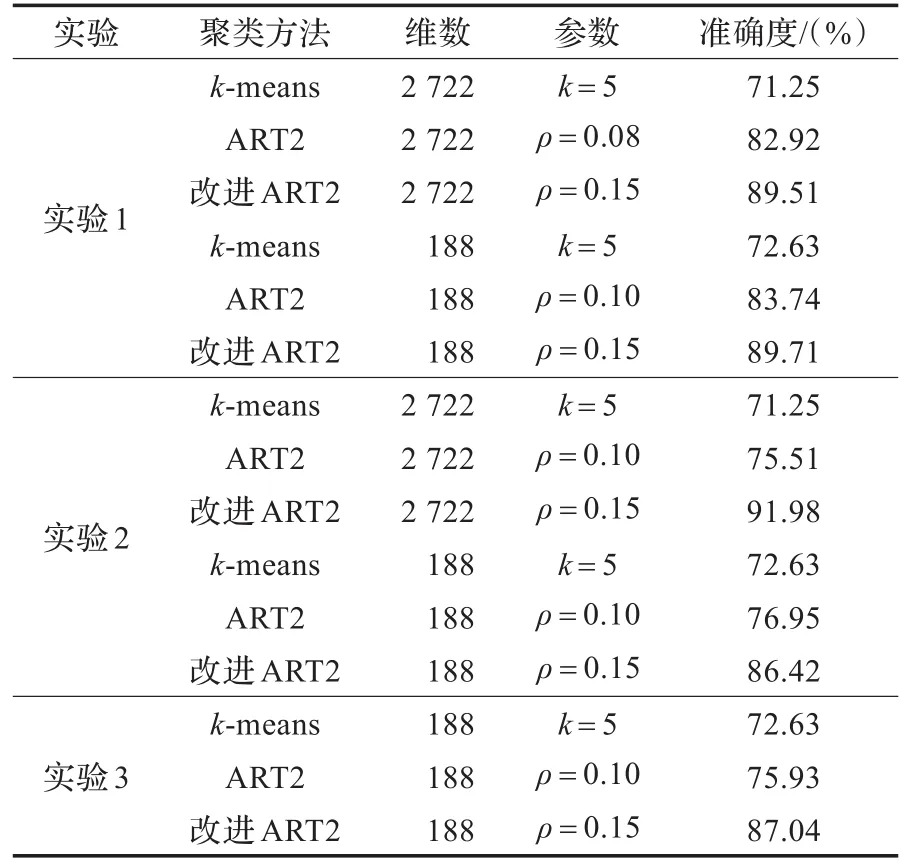
表1 實驗結果

（1）通過比較聚類算法在未降維和經過LSA降維之后的聚類結果可得，LSA降維之后可以突出潛在文本隱含語義，加強相同聚類簇實體的相似性及不同聚類簇實體間的差異，使得聚類分析結果更加準確，并且數據降維能有效地降低計算復雜度，從而加快聚類算法的處理速度。

（2）通過實驗1和實驗2可得，改進后的ART2網絡能大大提高傳統ART2網絡的穩定性及準確性，并且其準確性比k-means算法高而穩定性與k-means算法相近。由于k-means算法通過全局迭代并以最小二乘方作為評價函數，聚類結果對順序的依賴非常小，而由上分析可得數據輸入順序直接決定了ART2網絡的LTM初始值，故其對數據輸入順序的依賴較大，而在引入最近鄰重組后，改進的ART2網絡有效地減弱了對于輸入順序的依賴。

（3）由實驗3可得，只要在同一個向量空間的數據ART2網絡以及改進后的ART2網絡都可以在原有基礎上進行聚類，而k-means算法無法實現。由于ART2網絡及改進后的ART2網絡的聚類分析實際上是由數據與神經元之間關系確定，從而可在原有聚類基礎上進行再次聚類，而k-means算法對新的數據需要采用全局迭代過程才能最終確定聚類結果。

從實驗結果可以得出，改進后的ART2網絡在聚類結果的準確性和穩定性均優于傳統ART2網絡的聚類結果。

6 結束語

本文研究表明，使用ART2網絡進行文本聚類，能夠有效和動態地對文本數據進行聚類分析。但一方面由于文本數據的高維性，所以結合LSA合理地進行降維能夠更好地得出聚類結果，另一方面ART2網絡為了實現動態性，在一定程度上犧牲了穩定性，所以在低閾值的情況下，表現出對輸入順序的敏感。本文通過最近鄰關系重組，在一定程度上改善了這個問題并且保留了ART2網絡的高動態性，但仍然有較多的問題遺留等待研究：

（1）由于ART2網絡能夠自動生成聚類個數，所以實現無需估計聚類個數。而ART2網絡的聚類個數主要是由警戒閾值 ρ決定，而如何確定警戒閾值目前還只能通過統計，或者多次測試等手段獲取，如何更方便地獲取有效的警戒閾值ρ是一個值得研究的方向。

（2）由于最近鄰關系是一種全局關系，所以能夠在一定程度上確定實體之間的關系，而不依賴輸入順序的改變，但是最近鄰關系并不是一種嚴格的全局關系，當存在“平局”現象時，則此時即使是最近鄰關系依然依賴輸入順序，所以如何更好地解決這種“平局”現象使實體之間的關系更加確定也是一個需要研究的問題。

（3）LSA理論是一種有效的降維方法，不僅能夠有效減弱原文本-詞條矩陣中包含的“噪聲”因素，使文本和詞條之間的語義關系更加凸現出來；而且降維后使文本-詞條向量空間大大縮減，減少了數據計算量，從而提高文本聚類的處理效率。但是由于文本間的相互關聯性較為復雜，文本特征的高維性，如何合理地選取文本特征、確定降維規模、有效地處理文本的多個主題仍然是一個值得研究的問題。

[1]Salton G，Wong A，Yang C S.A vector space model for automatic indexing[J].Communications of the ACM，1975，18（11）：613-620.

[2]Salton G，Buckley C.Term-weighting approaches in automatic text retrieval[J].Information Processing and Management，1988，24（5）：513-523.

[3]Landauer T K，Foltz P W，Laham D.An introduction to latent semantic analysis[J].Discourse Processes，1998，25（2/3）：259-284.

[4]Han Jiawei，Kamber M.Data mining：concepts and techniques[M].USA：Morgan Kaufmann，2001.

[5]Kohonen T，Somervuo P.Self-organizing maps of symbol strings[J].Neuro Computing，1998，26（5）：19-30.

[6]Carpenter G A，Grossberg S.A massively parallel architecture for a self-organizing neural pattern recognition machine[J].Computer Vision，Graphics and Image Processing，1987，37（1）：54-115.

[7]Carpenter G A，Grossberg S.ART-2：self-organization of stable category recognition codes for analog input pattern[J].Applied Optics，1987，26（23）：4919-4930.

[8]Carpenter G A，Grossberg S，Rosen D B.ART2-A：an adaptive resonance algorithm for rapid category learning and recognition system[J].Neural Network，1991，4：493-504.

[9]葉曉明，林小竹.慢速權值更新的ART2神經網絡研究[J].計算機工程與應用，2010，46（24）：146-150.

[10]韓小云，劉瑞巖.ART-2網絡學習算法的改進[J].數據采集與處理，1996，11（4）：241-245.

[11]劉力，胡博，史立峰.ART2神經網絡綜述[J].中南大學學報：自然科學版，2007，38（1）：21-26.

[12]諶海霞.ART2網絡的學習速率調整及其影響[J].微電子學與計算機，2008，25（9）：147-150.

[13]呂秀江，王鵬翔，王德元.基于ART2神經網絡算法改進的研究[J].計算機技術與發展，2009，19（5）：137-139.

[14]顧民，葛良全.一種ART2神經網絡的改進算法[J].計算機應用，2007，27（4）：945-947.

[15]高茂庭，王正歐.基于LSA降維的RPCL文本聚類算法[J].計算機工程與應用，2006，42（23）：138-140.

[16]林鴻飛.基于實例的文本標題分類機制[J].計算機研究與發展，2001，38（9）：1132-1136.

[17]海量公司.中文智能分詞[EB/OL].[2012-12-20].http：//www. hylanda.com/dowmload/segment/.

XU Chenkai,GAO Maoting

College of Information Engineering,Shanghai Maritime University,Shanghai 201306,China

In order to realize dynamic clustering for high-dimensional text data,an improved ART2 neural network text clustering algorithm based on Latent Semantic Analysis（LSA）is proposed,which emerges the semantic relations between texts and terms and reduces the noises,the dimensionality and the computation complexity by LSA.The new algorithm uses an improved intermediate learning method to simplify calculating procedures and accelerate the computation of the ART2 network,and uses the nearest neighbor reformation to improve the stability and weaken the dependence of samples order for the ART2 network clustering.Experiments demonstrate that this improved algorithm can realize dynamic text clustering effectively.

ART2 neural network;nearest neighbor;Latent Semantic Analysis（LSA）;dimensionality reduction;text clustering;clustering analysis

針對文本數據高維度的特點和聚類的動態性要求，結合隱含語義分析（LSA）降維，提出一種改進的ART2神經網絡文本聚類算法，通過LSA凸顯文本和詞條之間的語義關系，減少無用噪聲，降低數據維度和計算復雜性；采用改進的折中學習方法，減少計算步驟，加快ART2神經網絡計算速度，并利用最近鄰動態重組方法提高ART2網絡聚類的穩定性，減弱算法對樣本輸入順序的依賴。實驗表明，改進的文本聚類算法能有效地實現動態文本聚類。

ART2神經網絡；最近鄰；隱含語義分析（LSA）；降維；文本聚類；聚類分析

A

TP183

10.3778/j.issn.1002-8331.1302-0109

XU Chenkai,GAO Maoting.Improved ART2 neural network for text clustering based on LSA.Computer Engineering and Applications,2014,50（24）：133-138.

上海市科委科技創新項目（No.12595810200）；上海海事大學科研項目（No.201100051）。

徐晨凱（1989—），男，碩士研究生，CCF學生會員，主要研究領域：數據挖掘；高茂庭（1963—），男，博士，教授，系統分析員，CCF高級會員，主要研究領域：數據挖掘，數據庫與信息系統。E-mail：kk9265w@gmail.com

2013-02-20

2013-04-11

1002-8331（2014）24-0133-06

CNKI網絡優先出版：2013-05-13，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130513.1601.002.html