基于雙種群交流粒子群算法的離散投資組合模型

王秀利，劉 洋

中央財經大學 信息學院，北京 100081

基于雙種群交流粒子群算法的離散投資組合模型

王秀利，劉 洋

中央財經大學 信息學院，北京 100081

1 引言

均值-方差模型[1]尋求在一定收益水平下風險最小，或在一定風險水平下收益最大。但該模型基于一系列嚴格假設，與實際證券市場投資環境存在很大差異，因此，考慮買空賣空限制、整數手數交易、交易費用等實際因素，提出一種符合當前我國證券投資市場的更完善的投資組合模型。其求解方法有人工神經網絡方法[2]、進化算法[3]、模糊系統[4]等，這些算法需要交叉、變異等特殊處理操作或對目標函數的特征有著嚴格要求。

粒子群算法（Particle Swarm Optimization，PSO）無需交叉、變異，對目標函數無特殊要求，被廣泛應用于模糊系統控制、神經網絡訓練、函數優化、工程應用[5-6]中，但其后期收斂速度慢，面對多極值問題時容易陷入局部最優。其改進算法有以下幾種：將不同的算法與PSO嵌入，優勢互補[7-8]；采用新的學習策略更新位置和速度[9]；改變搜索環境或搜索狀態[10]等。

用改進PSO算法求解投資組合問題取得了很多成果，但也存在不足之處，如文獻[11]將捕食策略引入PSO，提高了搜索精度，但增大了時間復雜度，同時算法最終可能出現不可能解，投資組合模型中忽略了投資者偏好；文獻[12]引入遺傳算法提高了PSO算法的搜索性能，并能夠找到風險更小的投資組合，但新算法因復雜的“交叉”操作而使PSO失去了簡單易行的最大優勢，并且沒有考慮完整的交易費用等實際因素；與本文相似，文獻[13]同樣在標準PSO中引入了兩個種群，但是學習過程中粒子的行動受到速度范圍的制約，跳出局部極值的可能性很小，很可能學習失敗，且速度的變異方式無根據可循。

本文以被學習種群作為標尺，由學習種群根據一定標準進行速度變異從而向新區域探索，不改變空間復雜度，收斂速度更快，精度更高。本文把基于雙種群交流的離散PSO算法應用于符合我國實際情況的證券投資組合模型中，實現了最優化求解。

2 基于雙種群交流的粒子群算法

標準PSO算法在適應度函數存在多極值時很容易陷入局部最優，雙種群交流的PSO算法針對這一缺陷進行改進。

雙種群交流PSO將粒子初始化為兩個種群，即swarm1與swarm2，二者更新時互不干擾，到目前為止找到的最優適應度值分別為 fpg1和 fpg2，令 fpg=max(fpg1，fpg2)，直到連續K次 fpg都不變，兩個種群開始交流。

2.1 雙種群交流步驟

2.1.1 確定（被）學習種群

以目前 fpg為標準，按照模擬退火算法公式，對swarm1有：

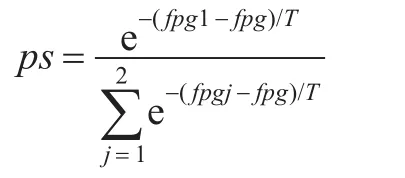
若 ps＜rand()，則被學習種群為swarm1；反之被學習種群為swarm2。其中T為退火溫度。采用上述方法后，使得目前最大適應度相對較壞的種群也有可能成為被學習對象。

2.1.2 確定學習種群的學習概率

根據學習種群中每個粒子自身到目前為止搜索到的歷史最優適應度值大小對粒子進行連續編號。由于歷史最優適應度值越大，該粒子對其他粒子的吸引力越強，為防止局部最優，就越需要向外界學習從而對其位置進行變異，該粒子編號應該越大。第i個粒子的學習概率為 pdi=0.5×(numberi/N)5+0.1，其中numberi是學習種群中第i個粒子的編號，N為學習種群規模。

2.1.3 更新粒子的速度與位置

被學習種群按照標準PSO更新速度與位置。學習種群中每個粒子都要根據學習得來的信息以新方式更新速度和位置。

當 pdi＞rand()時，該粒子向被學習種群靠攏，所涉及的區域相對當前位置而言在被學習種群一側。速度更新公式如下（以swarm1向swarm2學習為例，下同）：

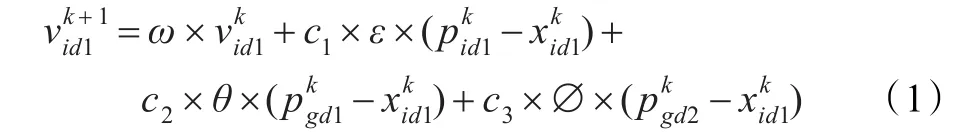
其中?為[0，1]之間的隨機變量。位置更新公式如下：

為了在學習中讓粒子盡可能大步邁出當前的局部機制，突破速度范圍的限制，引入速度約束因子γ，在更新位置時，起到調節速度的作用。γ的大小設置與速度的范圍限制有關，設置原則是使該速度變異的粒子能夠跳出當前的局部最優區域，盡可能向更大范圍探索。如本文中速度的范圍被設置為搜索空間范圍的0.2倍，則γ設置為2.5，使得該粒子一次速度變異能夠飛行的距離約為整個搜索空間的一半。經本文多次測試可知，當γ過小時，粒子很可能無法跳出當前局部極值區域，本次粒子學習失敗；當γ過大時，往往會使粒子學習后的新位置溢出搜索空間邊界，最終被重置于某一特定位置，這樣很多粒子速度變異后都集中在被特設的區域，無法盡可能分散到整個搜索空間，會削弱整個種群的搜索能力。

當 pdi＜rand()時，該粒子向被學習種群背離，所涉及的區域相對當前位置而言在被學習種群一側的相反方向。目的是覆蓋整個搜索區域。速度更新公式如下：

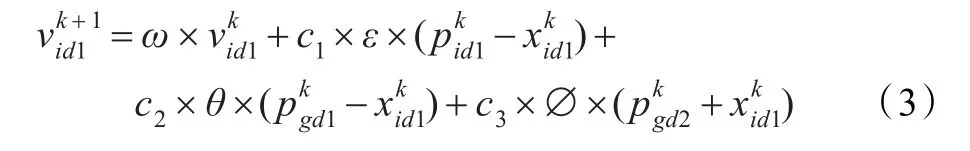
位置更新同公式（2）。

對于粒子位置的離散約束和范圍約束采用懲罰函數的方法進行處理。

2.2 雙種群交流流程圖

雙種群交流PSO算法流程圖如圖1所示。

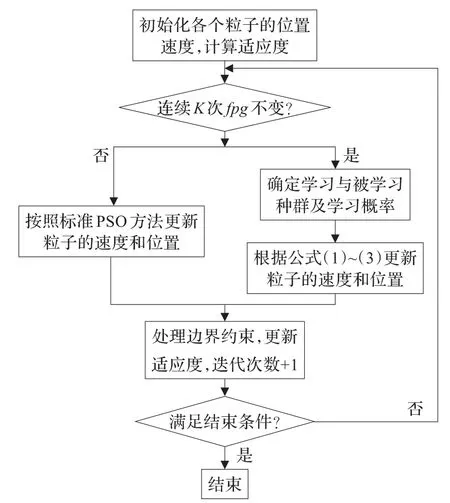
圖1 雙種群交流PSO流程圖

3 符合我國實際情況的投資組合模型

3.1 投資組合約束函數

假設投資總額為total，投資比例向量為 x={x1，x2，…，xn}′，xi表示投資于每種風險資產的權重，σ表示每種風險資產收益率變化之間的協方差矩陣，即風險程度的衡量；Ri(i=1,2,…，n)表示第i種風險資產的預期收益率。

我國證券市場上存在以下幾種限制因素：

（1）買空賣空限制：不允許買空與賣空，則0≤xi≤1。

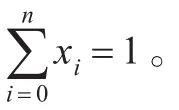
（4）交易費用：上證交易所買入股票的成本有：

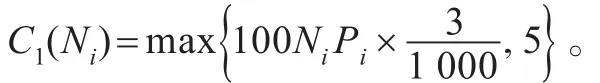
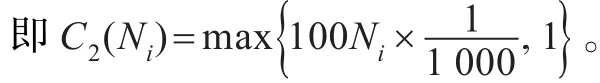
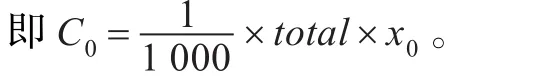
3.2 投資組合目標函數

在風險一定時，投資者會選擇收益較大的組合；而在收益一定時投資者會選擇風險較小的組合。其目標函數為：

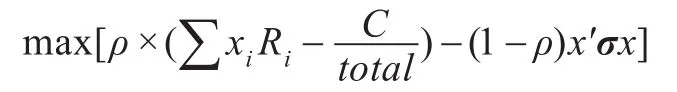
投資者可根據對風險的厭惡程度選擇不同的系數ρ。

綜上可得符合我國實際情況的投資組合模型為：

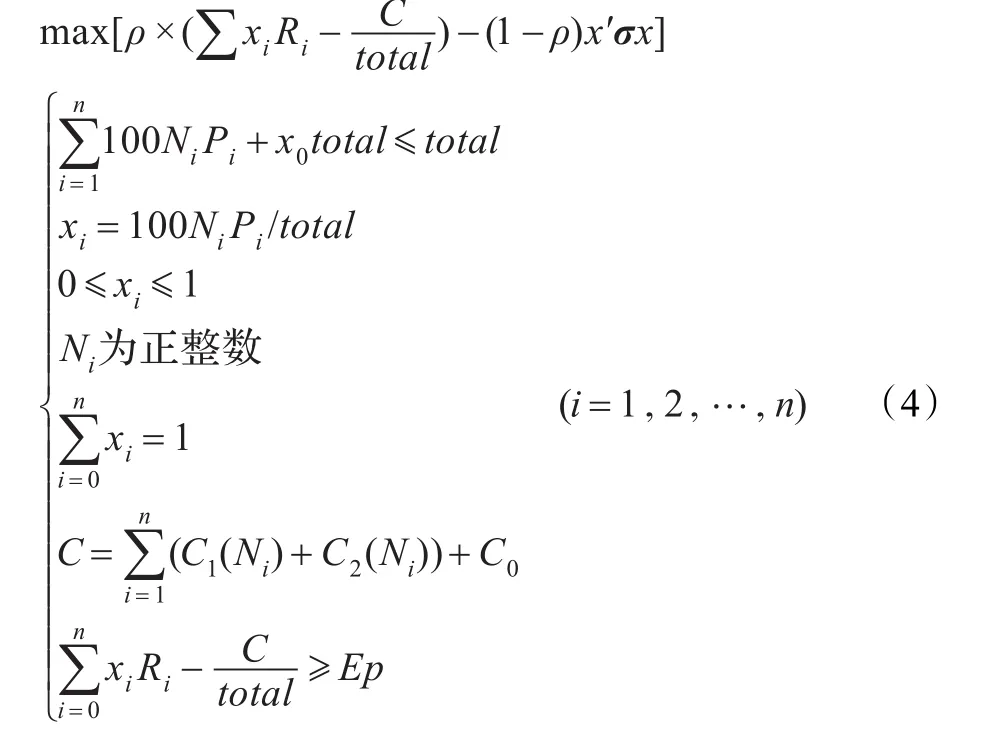
4 投資組合模型求解

4.1 樣本與數據來源

由于2013年我國尚未發行一年期國債，所以使用三年期國債的年利率作為無風險收益率，為4.76%。本文所選股票全部來自上證A股，在農林牧漁、采礦業、建筑業、信息技術業、金融業、住宿和餐飲、水電煤、房地產、文化和社會工作、文化體育娛樂10個行業中選取了50支股票，利用2010、2011、2012全年收益率和2013第一季度收益率作為處理股票預期收益率的依據，并據其計算每只股票之間的協方差以衡量風險，實證所需要的股票價格和收益率等數據全部來自于“東北證券網上交易V6”平臺。50只股票的基本情況如表1所示。

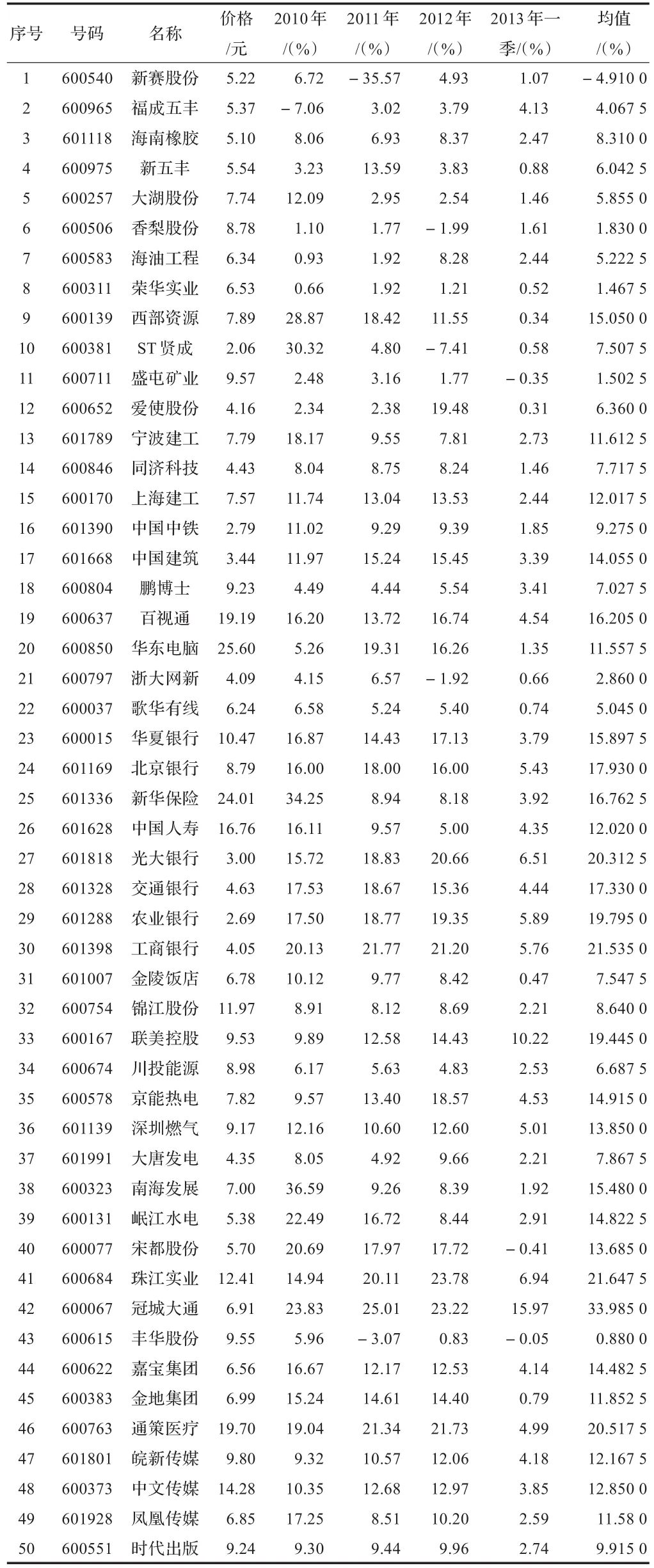
表1 上證交易所50支股票部分近年收益數據

表2 最優投資組合（期望收益率為8%時）1）

表3 最優投資組合（期望收益率為9%時）1）

表4 最優投資組合（期望收益率為10%時）1）

表5 最優投資組合（期望收益率為11%時）1）

表6 最優投資組合（期望收益率為12%時）1）

4.2 結果與分析

將50只樣本全部引入模型，由投資者預期收益率、手數為整數、投資組合公式等作為約束條件，自由選擇股票，并給出所投資的手數、組合的期望與標準差。初始投資額total為100萬元。使用MATLAB編程所得最優投資組合如表2～表6所示。

由上述結果可以看出：

（1）隨著投資者的期望收益率不斷增加，標準差也不斷增加，這符合風險收益正相關原理。

（2）在該模型中投資者可以根據自己對市場的預期改變其期望收益率，獲得不同的投資組合。

（3）投資組合中，影響不同行業不同股票的非系統性風險不同，可能相互抵消，只需選擇若干只收益率相關系數較小的股票進行投資即可，盡可能多地選擇股票進行投資是沒有意義的，因此該模型能對股票數目和種類進行自主選擇。

（4）該模型能夠按照我國股票市場上整數手數投資、買空賣空限制、交易費用限制、投資總金額有限等多種實際情況，有效指導投資者進行投資。

5 結束語

將改進的雙種群交流離散PSO算法應用到我國股票市場上，不僅能夠指導投資者選擇股票種類進行組合，更能給出投資的比例，是一種切實可行的指導投資者構造資產組合的方法。

[1]Markowitz H W.Portfolio selection[J].Journal of Finance，1952，7（1）：77-91.

[2]辛沂.Hopfiel神經網絡的穩定性及其在投資組合理論中的應用[D].濟南：山東大學，2008.

[3]牛雪麗.差分進化算法及其在金融產品組合優化中的應用[D].濟南：山東師范大學，2009.

[4]陳國華，廖小蓮，余星.基于直覺模糊規劃的多目標投資組合選擇模型[J].模糊系統與數學，2012，26（2）：129-135.

[5]張長勝，孫吉貴，歐陽丹彤.一種自適應離散粒子群算法及其應用研究[J].電子學報，2011，37（2）：299-304.

[6]于穎，李永生，於孝春.粒子群算法在工程優化設計中的應用[J].機械工程學報，2008，44（12）：226-231.

[7]趙學奇.模擬退火改進的粒子群算法的研究及應用[D].武漢：華中科技大學，2012.

[8]黃太安，生佳根，徐紅洋，等.一種改進的簡化粒子群算法[J].計算機仿真，2013，30（2）：327-335.

[9]Wang X L.A model for portfolio selection based on particle swarm optimization with escape velocity[C]//International Conference on E-Business and E-Government，2010：3513-3516.

[10]陳炳瑞，馮夏庭.壓縮搜索空間與速度范圍粒子群優化算法[J].東北大學學報，2005，26（5）：488-491.

[11]劉冬華，甘若迅，樊鎖海，等.基于捕食策略的粒子群算法求解投資組合問題[J].計算機工程與應用，2013，49（6）：253-256.

[12]何光，吳萌.基于改進粒子群算法的投資組合模型[J].計算機仿真，2013，30（2）：209-212.

[13]秦全德.粒子群算法研究及應用[D].廣州：華南理工大學，2011.

WANG Xiuli,LIU Yang

School of Information,Central University of Finance and Economics,Beijing 100081,China

Considering that standard Particle Swarm Optimization（PSO）has the severe problem of being stuck in local optimums,this paper puts forward an improved particle swarm optimization with two particle swarms communicating with each other on the basis of velocity mutation,leading to the problem above to be resolved.In addition,taking into account the existence of transaction cost and the restraints of long sale,short sale,integral number of transactions and so on in China, this paper builds a portfolio selection model which totally reflects current status in our country.It applies the improved PSO above to deal with the model.The result comes out that the model is integrated and effective in our country,and also the PSO with two particle swarms communicating with each other is proper and efficient.

two particle swarms communicating with each other;Particle Swarm Optimization（PSO）;portfolio selection model

針對標準粒子群算法易陷入局部最優的缺陷，提出一種雙種群交流的新型粒子群算法，利用速度變異成功地解決了上述問題；綜合考慮了我國股票市場上的交易費用、整數手數投資、不允許買空賣空等問題，建立了符合我國股票市場的投資組合模型，并將雙種群交流的離散粒子群算法應用于其求解過程中，給出最優投資組合。

雙種群交流；粒子群優化；投資組合模型

A

TP399；F830.59

10.3778/j.issn.1002-8331.1308-0207

WANG Xiuli,LIU Yang.Discrete portfolio selection model based on particle swarm optimization algorithm with two particle swarms communicating with each other.Computer Engineering and Applications,2014,50（24）：227-230.

國家自然科學基金（No.61272398）；國家社會科學基金重點項目（No.13AXW010）；中央財經大學學科建設基金項目。

王秀利（1977—），男，博士，副教授，CCF高級會員，研究領域為信息經濟、優化理論及應用。E-mail：xlwang.cufe@gmail.com

2013-08-15

2013-09-30

1002-8331（2014）24-0227-04

CNKI網絡優先出版：2014-07-11，http∶//www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1308-0207.html