基于模糊積分的供應鏈網絡優化方法

張國防，何莉輝

河北大學 數學與計算機學院，河北 保定 071002

基于模糊積分的供應鏈網絡優化方法

張國防，何莉輝

河北大學 數學與計算機學院，河北 保定 071002

1 引言

從供應鏈角度而言，成功選擇合作伙伴至關重要，供應鏈網絡設計中最主要的任務就是優勢企業依據技術、質量、成本、時間、產能等特性，從每一層次候選企業中選擇良好的合作伙伴，從而確定產品從原材料起點到顧客端點的整個流程網絡。文獻[1]提出了基于自我分類理論的供應鏈合作伙伴選擇的兩階段模型。該模型提出了供應鏈合作伙伴選擇應在企業去人格化后，在自我分類的基礎上選擇與核心企業核心能力互補且具有競爭力的合作伙伴的觀點，為供應鏈合作伙伴選擇提供了新思路。文獻[2]從供應鏈合作伙伴選擇角度出發，討論了基于GBOM的供應鏈網絡的結構，在此基礎上建立了供應鏈合作伙伴選擇的數學模型，給出了模型的求解方法。文獻[3]選擇最小二乘支持向量機（LS-SVM）算法對合作伙伴進行選擇。傳統供應鏈網絡設計問題的研究中，文獻[4]利用模糊事件的可信性測度推導零售商的模糊期望利潤，運用logit模型刻畫消費者的隨機選擇行為，借助有限維變分不等式理論構建具有模糊需求的多商品流供應鏈網絡均衡狀態滿足的變分不等式。而在文獻[5]中，研究了供應商向制造商供應原材料，生產同質產品的制造商通過零售商銷售渠道將其產品銷售給消費者，以滿足消費市場隨機需求的供應鏈網絡最優化問題。然而在供應鏈網絡設計時所依據的數據大多是模糊與隨機雙重不確定性的。諸多的模糊和隨機雙重不確定性給供應鏈網絡構建帶來了困難。因此本文引入模糊理論和隨機理論研究供應鏈合作伙伴選擇與網絡構建方法。

在實際的決策過程中，由于客觀事物的復雜性、隨機性及人類思維的模糊性，決策者在對事物進行判斷評估時，提供的偏好信息有可能無法采用精確的數值來進行估計，一般喜歡直接用模糊和隨機雙重語言形式給出，決策者對不同類別屬性的綜合過程帶有很強的主觀思考或經驗推理，所以這也是一個對離散信息、帶有隨機性和模糊偏好的模糊綜合過程。文獻[6]利用博弈理論構建了分散式控制生產商與零售商的Stackelberg博弈模型和集中式控制閉環供應鏈的決策模型，通過求解模型得到了各成員企業和閉環供應鏈的最優決策及利潤。文獻[7]利用模糊理論的期望值模型，分別在集中式和分散式兩種決策方式下給出了新產品的最優批發價格、最優零售價格及廢舊產品的最優回收率的解析表達式。但是上述方法中所使用的決策工具只考慮了單個屬性的重要程度，沒有考慮屬性之間的交互性對整個決策的影響。因此本文引入模糊測度和模糊積分理論研究供應鏈合作伙伴評價與選擇的多重多屬性模糊綜合決策，以及模糊隨機環境下的任務粗分配方法。下面對本文使用的gλ模糊測度和choquet模糊積分做簡單的介紹[8]。

2 gλ模糊測度與choquet模糊積分

2.1 gλ模糊測度

本文中，供應鏈合作伙伴選擇與網絡構建中涉及的是有限個屬性，討論的內容主要是基于有限集合，所以假定有限集合 X={x1，x2，…，xn}，有限集上的模糊測度在數學中的定義如下：

定義1假設 X為非空集合，P(X)為由 X的子集構成的冪集，集函 μ∶P(X)→[0，1]滿足下面的三個性質時，稱為定義在P(X)上的模糊測度：

（1）μ(?)=0，μ(X)=1（歸零性，正則性）

（2）A∈P(X),B∈P(X),B?A?μ(B)≤μ(A)（單調性）

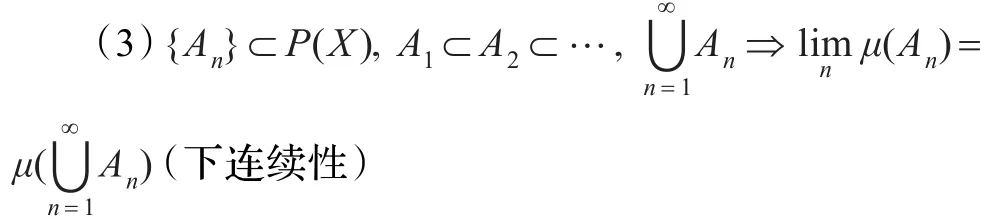
定義2如果模糊測度g還滿足下面性質時，那么稱之為gλ-模糊測度（Sugeno模糊測度）。

存在常數λ，λ＞-1，使得：

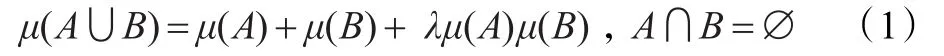
通常將 gλ-模糊測度記為 g，令 g({xi})=gi，i=1，2，…，n，xi∈X，稱gi為模糊密度。模糊密度gi可以解釋為供應鏈合作伙伴選擇與網絡構建中第i個屬性的重要程度。關于gλ-模糊測度有下面兩個重要的結論：

定理1設 g為定義在 P(X)上的 gλ-模糊測度，A1，A2，…，Al為P(X)中互不相交的l個集合(0＜l≤2n= |P(X)|)，則

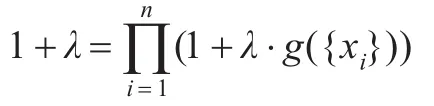
由定理1和定理2可知，模糊測度 g在集合 X= {x1，x2，…，xn}中每一單點集的模糊測度值能確定 g在P(X)中其他集合的模糊測度值，因此在供應鏈合作伙伴選擇與網絡構建中，要確定gλ-模糊測度，只需知道模糊密度，即只要確定各個屬性的重要度就可以了。

2.2 choquet模糊積分

定義3假設 f為定義在 X上的非負函數，μ為定義在F上的模糊測度，F為由X的子集構成的σ-代數（當X為有限集合時，F=P(X)），則 當X={x1，x2，…，xn}為有限集合時，令·(i)滿足條件：

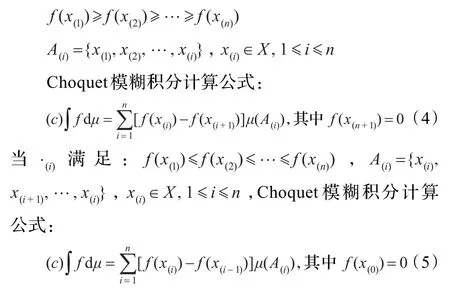
3 基于模糊積分的合作伙伴選擇模糊多屬性綜合決策

3.1 供應鏈合作伙伴評價屬性模糊隨機變量和隨機模糊變量

本文以文獻[9]中提供的供應鏈合作伙伴評價多屬性層次分析結構模式為依據研究模糊和隨機雙重不確定性環境下的合作伙伴選擇。在模糊與隨機雙重不確定性環境下得到的各屬性分量的參數值均為模糊隨機數值，或為隨機模糊數值，或為定量絕對模糊隨機數，或為定性隨機模糊語意。屬性變量取值為模糊隨機型時，首先將模糊語意與相應的定義于[0，1]的模糊三角數或模糊區間數匹配，進行數量化轉換，然后根據模糊隨機型取值的概率分布計算出期望值作為最終參與決策的數值。屬性變量取值為隨機模糊型時，首先依據隨機性計算出期望值，然后將模糊語意與相應的定義于[0，1]的模糊三角數或模糊區間數匹配，進行數量化轉換。

3.2 離散信息各屬性及屬性子集模糊測度的確定

根據前面的敘述，只要確定出各個單個屬性的重要度，即測度值，那么由公式（2）可以完全確定gλ模糊測度，這樣屬性子集的測度值給出了屬性之間交互性的一種度量。接下來的問題是如何將這些模糊語意量子在不確定性最小情況下轉換為相應的單個屬性的重要度。由于模糊語意量子具有單調性，故模糊語意決策的屬性重要度向量由下式確定[10]：

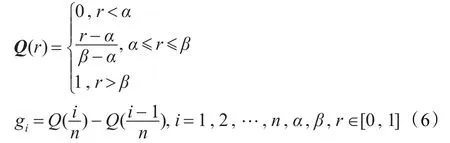
為了評價決策者在模糊語意下的決策狀態，給出相應屬性重要度向量的orness（或的程度）和entropy（熵）兩種測度，即

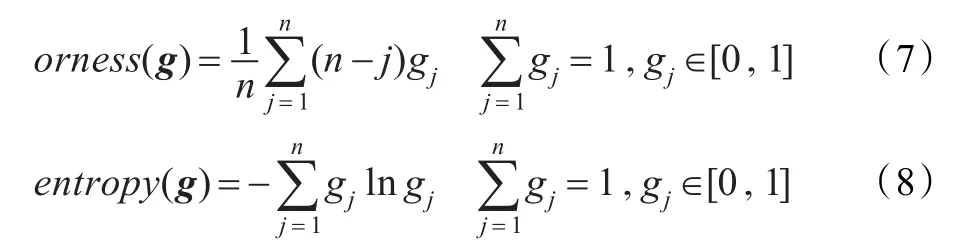
在多屬性決策中如何確定各屬性的重要度向量，為了盡量減小各屬性重要度系數的不確定，根據Jaynes最大熵原理[11]，所確定的屬性重要度向量應使entropy取極大。結合文獻[12]中的方法，假設在供應鏈合作伙伴選擇與網絡構建中有n個屬性用gi，(i=1，2，…，n)表示模糊密度，即 gi=μ({x(i)})，為單個屬性重要程度的度量，X={x1，x2，…，xn}表示n個屬性集合。gλ模糊測度測度確定步驟如下：

步驟1由式（6）得到屬性重要度初始向量 g= (g1，g2，…，gn)。

步驟2由式（7）計算屬性重要度向量g的orness(g)值。

確定模糊測度值。

3.3 基于模糊積分的模糊多屬性綜合決策

本文采用文獻[9]中的供應鏈關系關聯度定義，結合模糊測度的確定方法，由屬性重要性程度與決策過程信息取舍多少模糊語意進行匹配可以確定不同屬性的重要度，以choquet模糊積分作為決策工具對各個屬性子集進行信息融合，得到各個屬性的數值信息。所以，合作伙伴選擇的決策過程如下：

步驟1優勢企業（盟主）所委托或指定的決策專家小組根據產品類型、生產任務、供應鏈策略等提出伙伴企業選擇評價的屬性，對大的屬性可繼續分解為具體的實施細則即相應的子屬性，依AHP模式建立比較全面、詳細的評價屬性體系。

步驟2采用交互方式，依據評價指標體系充分征詢候選企業，分別采集候選企業對其上游企業或下游企業選擇的子屬性評價信息。通過對所采集的信息可進一步對AHP評價多屬性體系進行修正和完善。

步驟3對采集得到的定量子屬性信息和定性子屬性信息進行模糊語意轉化為相應的模糊數，對信息進行規范化處理。

步驟4根據多屬性體系中屬性或子屬性的向量個數，分別對綜合決策中的三種模糊語意：至少一半、絕大多數、盡可能多，利用gλ模糊測度測度確定步驟計算得到各個屬性的重要度以及屬性子集的重要度。

步驟5根據產品類型、生產階段和供應鏈策略，對AHP結構中的屬性按重要性程度進行分類，即哪些屬性為關鍵屬性，哪些屬性為重要屬性，哪些屬性為一般屬性。按關鍵屬性與至少一半匹配、重要屬性與絕大多數匹配、一般屬性與盡可能多匹配，以choquet模糊積分作為信息決策工具對各個屬性下的子屬性信息進行融合，得到各屬性數值信息。再按“絕大多數專家意見一致”這一語意進行屬性信息融合，得到伙伴關系選擇優屬度。

步驟6對相鄰層次上兩候選企業對各自對方的伙伴關系優屬度按乘積整合，得到兩兩候選企業間的伙伴關系關聯度。相鄰層次上伙伴關系關聯度應進行歸一化處理，最后數值大小表示合作伙伴關系選擇的優先順序。

4 面向任務預分配的供應鏈網絡

設一定時期內產品的市場需求總量為Q，供應鏈各層間的物料轉換關系為1。考慮各個企業的生產處理能力的約束。如果這些約束參量是模糊隨機的，且市場需求總量也是模糊隨機的，這時可以用模糊隨機規劃的期望值模型，并以伙伴關系關聯度作為任務分配的權重。

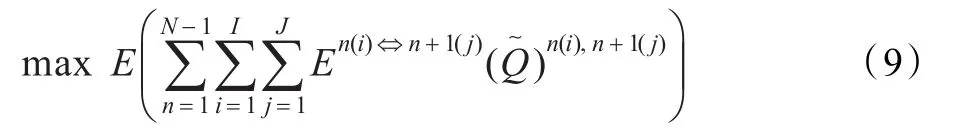
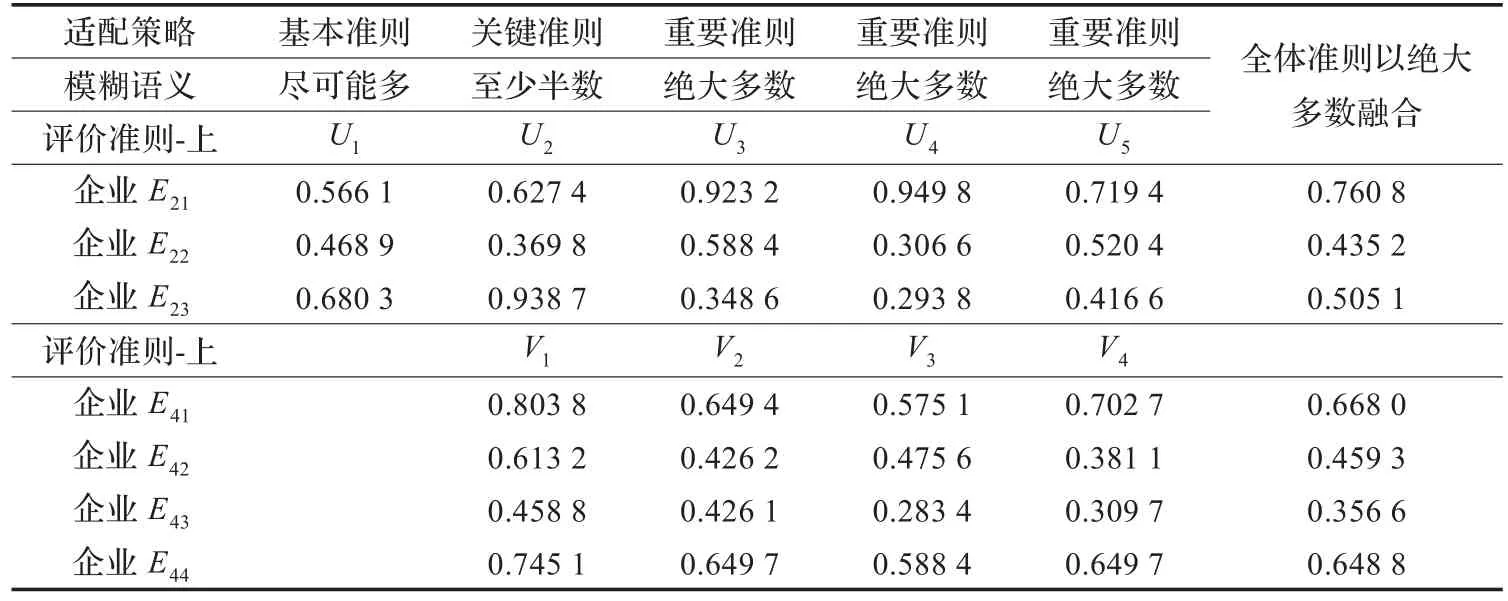
表1 評價時各準則適配策略和相應數據的模糊積分決策結果

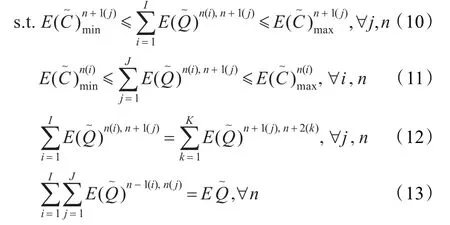
其中：式（10）（11）為企業的能力約束，式（12）為節點企業的物流約束，式（13）為需求約束。

為了求解上述模糊隨機規劃，參照文獻[13]中的方法，結合文獻[14-15]中的思路，采用由模糊隨機模擬，神經網絡及遺傳算法相結合而成的混合智能方法，其步驟如下：

步驟1通過模糊隨機模擬為不確定函數U產生輸入輸出數據。

步驟2利用產生的數據訓練一個神經網絡逼近不確定函數。

步驟3初始產生群體，并利用訓練好的神經網絡檢驗群體中個體的可行性。

步驟4通過交叉和變異操作跟新群體，并利用訓練好的神經網絡檢驗子代中個體的可行性。

步驟5利用訓練好的神經網絡計算所有個體的目標值。

步驟6根據目標值計算每個個體的適應度。

步驟7通過輪盤賭方法選擇個體。

步驟8重復步驟4到7直到完成給定的循環次數。

步驟9給出最好的個體作為最優解。

5 事例模擬

應用事例以某市輕紡區域網絡化制造為背景，考察某三個集團公司，該三個集團以生產加工運動服為主，利用本文提出的方法進行供應鏈構建與優化模擬，與文獻[3]、文獻[9]和文獻[13]中提出的方法進行對比，取五層{1-3-3-4-3}供應鏈網絡拓撲，以{N1-N2-N3-N4-N5}表示第一層企業 E11一家，第二層企業{E21，E22，E23}三家，第三層企業{E31，E32，E33}三家，第四層企業{E41，E42，E43，E44}四家，第五層企業{E51，E52，E53}三家。在供應鏈網絡構建過程中，首先進行的是合作伙伴評價與選擇，按決策流程評價準則，依照這些評價準則，各企業分別對各自上下游可合作伙伴進行評價。根據供應鏈策略確定各評價準則的重要性程度見表1。設一定時期內產品的市場需求總量為確定值，分別利用文獻[3]、文獻[9]、文獻[13]和本文提出的方法構建供應鏈網絡，以最終網絡的分配總量在市場需求總量中的比重為標準，實驗結果見表2。通過對實驗結果的分析，可以看出使用本文提出的方法較其他方法具有很好的結果，其主要原因是考慮屬性之間的交互作用，同時利用choquet模糊積分為決策工具可以將各個屬性之間的交互性進行有效的處理，這樣就盡可能地利用了數據提供的信息，保證較好的結果。

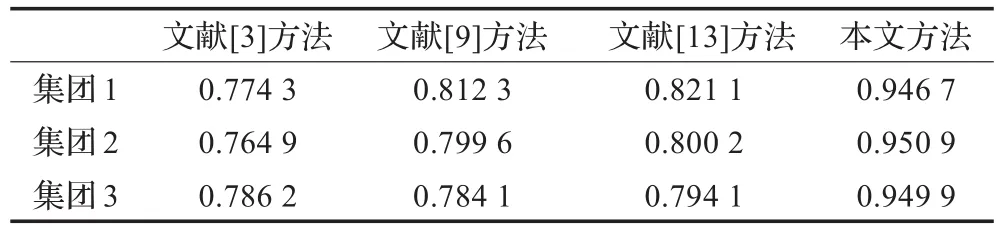
表2 各種方法得到的分配總量在需求總量中的比重結果

6 結論

本文分析了模糊與隨機雙重不確定環境下合作伙伴選擇與供應鏈網絡構建，給出了相應的基于模糊測度和模糊積分理論的決策模型。針對供應鏈合作伙伴多屬性評價與決策，采用模糊隨機變量和隨機模糊變量刻畫多屬性中定性參量與定量參量的模糊與隨機雙重不確定性，研究了基于供應鏈策略導向的模糊隨機多屬性數值融合與模糊綜合決策，還研究了以合作伙伴關系關聯度為依據，采用模糊隨機規劃期望值模型探討了面向任務預分配的供應鏈初始網絡確定方法，最后通過事例模擬進行了驗證。

[1]劉家國，趙金樓.基于自我分類的供應鏈合作伙伴選擇模型[J].哈爾濱工程大學學報，2011（6）.

[2]單汨源，蘭海豐，毛超.基于GBOM的供應鏈合作伙伴選擇[J].統計與決策，2011（12）.

[3]肖宇，朱敏，黃俊.基于LS-SVM的供應鏈合作伙伴選擇[J].計算機與數字工程，2010（9）.

[4]胡勁松，徐元吉，劉芳霞，等.具有模糊需求的多商品流供應鏈網絡均衡研究[J].控制與決策，2012（5）.

[5]張桂濤，孫浩，胡勁松，等.考慮風險的隨機需求供應鏈網絡均衡研究[J].復雜系統與復雜性科學，2012（4）.

[6]徐兵，吳明.雙營銷渠道閉環供應鏈決策模型與協調[J].西南交通大學學報，2012（6）.

[7]魏杰，馬茜，張新軍，等.模糊環境下閉環供應鏈定價決策研究[C]//中國自動化學會控制理論專業委員會C卷，第三十屆中國控制會議，2011.

[8]王熙照.模糊測度與模糊積分及在分類技術中的應用[M].北京：科學出版社，2008.

[9]傅玉穎.不確定情況下基于模糊集理論的庫存管理研究[J].系統工程理論與實踐，2005（9）.

[10]Herrera，Francisco，Martinez L.A 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on Systems，Man，and Cybernetics，2000，6：746-752.

[11]朱雪龍.應用信息論基礎[M].北京：清華大學出版社，2001.

[12]Filev D，Yager R R.Analytic properties of maximum entropy OWA operators[J].Information Sciences，1995，85：11-27.

[13]劉寶啶，趙瑞清，王綱.不確定規劃及應用[M].北京：清華大學出版社，2003.

[14]陳倩.區間模糊語言多屬性群決策方法及應用研究[J].計算機工程與應用，2012，48（33）：18-23.

[15]田衛東，張建良.證據理論與模糊距離不確定性信息融合方法[J].計算機工程與應用，2011，47（30）：148-151.

ZHANG Guofang,HE Lihui

College of Mathematics and Computer Science,Hebei University,Baoding,Hebei 071002,China

In this paper,some problems are represented under the fuzzy-random uncertain circumstances,which usually happen when cooperation partner is selected in supply chain management.Furthermore,three methods are proposed∶the first one is selection of cooperation partner of supply chain,the second one is construction way of supply chain networks, the last one is the rough allocation of task under fuzzy-random uncertain circumstances.In these methods,the important technology is the policy of supply chain management and the tool of decision is fuzzy integral.A simulation example is represented,which shows that the proposed methods are feasible.

supply chain;fuzzy-random;fuzzy measure;fuzzy integral

分析了模糊隨機雙重不確定性環境下供應鏈合作伙伴選擇時存在的問題，提出了由供應鏈策略為主導，以模糊積分為決策工具的模糊隨機多重多屬性供應鏈合作伙伴選擇與網絡構建方法，以及模糊隨機環境下的任務粗分配方法。通過事例模擬進行了驗證，結果表明所提方法有效可行。

供應鏈；模糊隨機；模糊測度；模糊積分

A

TP181

10.3778/j.issn.1002-8331.1305-0149

ZHANG Guofang,HE Lihui.Method based on fuzzy integral about construction and optimization of supply chain networks.Computer Engineering and Applications,2014,50（24）：231-235.

河北大學青年基金（No.2011Q12）。

張國防（1979—），男，講師，研究領域為機器學習、人工智能；何莉輝（1979—），通訊作者，女，講師。E-mail：helihui@hbu.cn

2013-05-14

2013-06-30

1002-8331（2014）24-0231-05

CNKI網絡優先出版：2013-09-12，http∶//www.cnki.net/kcms/detail/11.2127.TP.20130912.1436.011.html

book=235,ebook=240