空間分數(shù)階Klein-Gordon方程的一種有效數(shù)值算法

周 曉 軍

(廈門大學(xué)數(shù)學(xué)科學(xué)學(xué)院,福建 廈門 361005)

分數(shù)階微分方程已經(jīng)被廣泛應(yīng)用于自然科學(xué)的各個領(lǐng)域,并逐漸成為一個活躍的研究領(lǐng)域．分數(shù)階微分算子與整數(shù)階微分算子不同,它具有非局部性,從而非常適合用來刻畫現(xiàn)實生活中具有記憶和遺傳特性的材料．譬如:分形和多孔介質(zhì)中的彌散[1-2],電容理論[3],電解化學(xué)[4],生物系統(tǒng)中的電導(dǎo)[5],黏彈性系統(tǒng)量子力學(xué)[6-7],混沌同步[8]等等．然而,在這一領(lǐng)域還有許多未解決的問題,分數(shù)階微分方程解的物理意義還沒有確切的解釋．盡管如此,這一新的領(lǐng)域仍然是科學(xué)工作者廣泛關(guān)注的焦點．我們知道,大多數(shù)分數(shù)階微分方程是沒有準確解的,即使有解,多半也是級數(shù)表示,非常不便于實際應(yīng)用,因此,設(shè)計有效穩(wěn)定的數(shù)值算法求解分數(shù)階微分方程是迫切需要的．目前,分數(shù)階微分方程的數(shù)值解法主要有變分迭代法[9]、同倫攝動法[10-11]、Adomian分解法[12]、同倫分析法[13]、譜方法[14-15]等等．

Klein-Gordon方程是相對論量子力學(xué)和量子場論中的最基本方程,它是薛定諤方程的相對論形式,用于描述自旋為0的粒子，它是物理學(xué)中提出的一類非常重要的非線性發(fā)展方程,在數(shù)學(xué)物理、固態(tài)物理、非線性光學(xué)、量子場論[16]等領(lǐng)域有著極其重要的地位．關(guān)于它的理論和數(shù)值研究不斷呈現(xiàn),Li等[17]針對非線性Klein-Gordon方程,提出了一種保結(jié)構(gòu)的有限差分格式,即原問題離散后,離散格式仍然保有連續(xù)問題的能量守恒性質(zhì)．Bao等[18]對非相對論極限狀態(tài)下Klein-Gordon方程的數(shù)值算法做了詳盡分析和比較．

眾所周知,逼近論中常用正交多項式作為一組基底來表示微分方程的解．Legendre多項式在數(shù)值計算中被廣泛采用,陳一鳴等[19]運用Legendre 多項式求解變系數(shù)的分數(shù)階Fredholm積分微分方程．本文將用移位Legendre正交多項式來構(gòu)造分數(shù)階Klein-Gordon方程的有效數(shù)值算法,我們在時間方向用有限差分格式,空間用移位Legendre正交多項式來逼近,并給出了算法的矩陣表示,便于計算機編程實現(xiàn),將該算法用于線性和非線性的空間分數(shù)階Klein-Gordon方程求解中．?dāng)?shù)值結(jié)果證實了所提出的算法是有效可行的．

1 問題描述及一些記號

空間分數(shù)階Klein-Gordon方程為:

(x,t)∈(0,1)×(0,T)，

(1)

初始條件為:

u(x,0)=φ0(x),ut(x,0)=φ1(x),

(2)

邊界條件為:

u(0,t)=φ0(t),u(1,t)=φ1(t)，

(3)

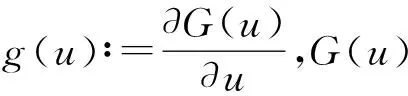
其中m是不小于α的最小整數(shù),記為m=α．Dm是m階經(jīng)典導(dǎo)數(shù),Iμ是Riemann-Liouville積分算子,定義如下：

由Caputo分數(shù)階導(dǎo)數(shù)的定義立即得到：

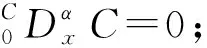
當(dāng)α>0,λ≥0時,有[20]

(4)

從純粹數(shù)學(xué)角度來看,Riemann-Liouville導(dǎo)數(shù)比Caputo導(dǎo)數(shù)更受歡迎,但在工程和數(shù)值計算上,在處理具體的物理問題時,Caputo導(dǎo)數(shù)只需給出在初始條件下的經(jīng)典導(dǎo)數(shù)的值,這樣導(dǎo)數(shù)就有明確的物理意義,然而,Riemann-Liouville導(dǎo)數(shù)需給出未知解在初始條件下的一些分數(shù)階導(dǎo)數(shù)的具體值,分數(shù)階導(dǎo)數(shù)可能沒有合適的物理意義,因此,人們更愿意采用Caputo導(dǎo)數(shù)．且由兩者的關(guān)系知道,在齊次條件下,Caputo導(dǎo)數(shù)和Riemann-Liouville導(dǎo)數(shù)是等價的．

2 移位Legendre多項式及其分數(shù)階導(dǎo)數(shù)

眾所周知,Legendre多項式,記為{Ln(z)},z∈[-1,1],是由勒讓德方程的通解推導(dǎo)出來的,Ln(z)滿足以下的奇異Sturm-Liouville方程

1)Ln(z)=0,z∈[-1,1].

關(guān)于Legendre多項式的遞歸關(guān)系是

L0(z)=1,

L1(z)=z,

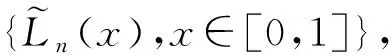
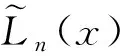
(5)

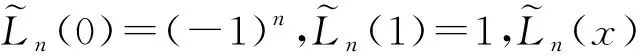
(6)

(7)

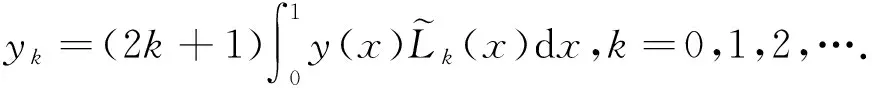
(8)

下面的定理給出了yN(x)的α階Caputo分數(shù)階導(dǎo)數(shù)的計算公式．

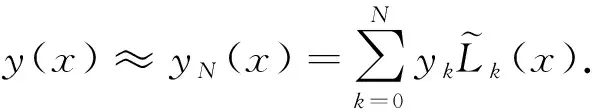
(9)

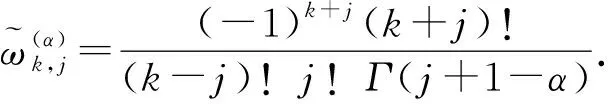
證明由Caputo分數(shù)階導(dǎo)數(shù)的定義可知,它是一個線性算子,因此有

(10)

由式(4),易知,

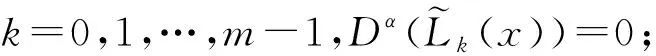
當(dāng)k=m,…,N,

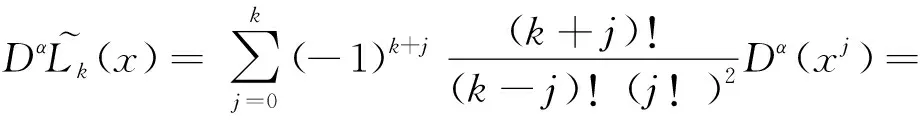
代入式(10)即得要證明的結(jié)果．

3 數(shù)值格式

問題(1)中,由于1<α<2,故m=α=2.為了構(gòu)造方程的數(shù)值格式,首先逼近u(x,t)為

(11)

將式(11)代入式(1),并應(yīng)用定理1,得到

g(uN(x,t))=f(x,t),

(12)

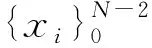
g(uN(xi,t))=f(xi,t),

i=0,1,…,N-2.

(13)

將式(11)代入式(3)得到

(14)

式(13)和(14)構(gòu)成了N+1維常微分方程組,未知量為u0(t),u1(t),…,uN(t)．

pmk=

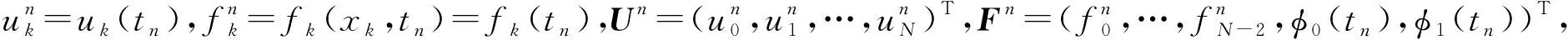
f(xi,t),i=0,1,…,N-2,n=1,2,…,M.

將上式與式(14)聯(lián)立,寫為矩陣形式是

P(Un+1-2Un+Un-1)-QUn+1+

g(PUn+1)=Fn+1.

(15)

注意:這里的g(PUn+1)是將函數(shù)g作用到向量PUn+1的每個元素上．

下面計算初始值U0,U1．由式(11)知

那么由正交性質(zhì)(6)有

k=0,1,…,N.

(16)

又因為

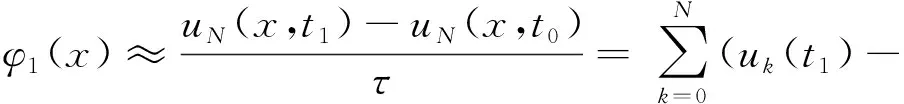
整理上式,并再一次由正交性質(zhì)(6)得到

k=0,1,…,N,

(17)

那么由(16)、(17),再通過式(15)就能夠求出U2,U3,…,UM．

特別地,(i) 取N=3,g(u)=u時,有

P=

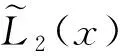
P(Un+1-2Un+Un-1)-QUn+1+PUn+1=Fn+1．

即

(2P-Q)Un+1=2PUn-PUn-1+Fn+1.

(18)

利用初始值U0,U1,通過式(18)容易求出U2,U3,…,UM．

(ii) 取N=3,g(u)=u3時,有

P(Un+1-2Un+Un-1)-QUn+1+

(PUn+1)3=Fn+1.

(19)

這是一個非線性的方程組,可以通過Newton迭代法來進行求解．

4 數(shù)值算例

首先,我們來看看分數(shù)階Klein-Gordon方程與整數(shù)階Klein-Gordon方程解之間的關(guān)系:

例1 考慮整數(shù)階Klein-Gordon方程:

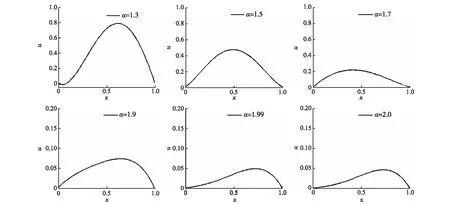
圖1 T=1,α=1.3,1.5,1.7,1.9,1.99,2,Δt=10-5,N=4時的解Fig.1 The solutions of (20) for T=1,α=1.3,1.5,1.7,1.9,1.99,2,Δt=10-5,N=4

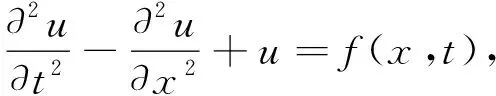
(x,t)∈(0,1)×(0,1)，

(20)

其中f(x,t)=-2x(x3-x2-6x+3)e-t,精確解為:u(x,t)=x3(1-x)e-t．

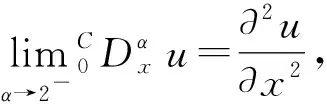
接下來,為了測試算法的有效性,用提出的數(shù)值格式(15)求解分數(shù)階Klein-Gordon方程．

例2 線性分數(shù)階Klein-Gordon方程

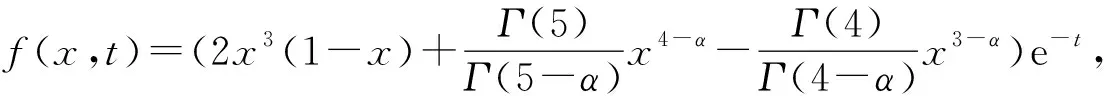
u(x,t)=x3(1-x)e-t．

為了觀察解的精度,圖2給出了數(shù)值解與它的精確解的對比,從圖中可以看出采用本文數(shù)值算法求得的數(shù)值解較好地擬合了精確解,數(shù)值算例進一步驗證了文中所給方法的可行性與有效性．

我們計算誤差error=‖u(x,T)-uN(x,T)‖L2隨著多項式次數(shù)變化的情況,見表1.我們?nèi)r間步長為Δt=10-5,當(dāng)多項式次數(shù)由3變?yōu)?時,誤差變化是極快的,在這里,由于時間僅僅是一階逼近,所以多項式繼續(xù)變化時,解的誤差也不會繼續(xù)縮小,這是符合實際情況的．值得指出的是,這里僅用4次正交多項式就能達到比較高的精度,說明數(shù)值格式是有效可行的．表2示出了固定多項式階數(shù)為N=4時,不同的時間步長下誤差的變化情況,從所列結(jié)果可以看出,誤差隨著時間步長的減小而急劇變小,說明算法是收斂的．

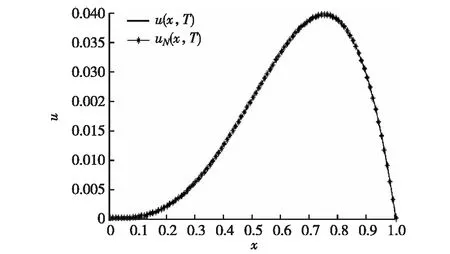
圖2 T=1,α=1.2,Δt=10-5,N=4時數(shù)值解 與準確解的比較Fig.2 The compare of numerical and exact solution for T=1,α=1.2,Δt=10-5,N=4.

例3 非線性分數(shù)階Klein-Gordon方程

(0,1)×(0,1)，

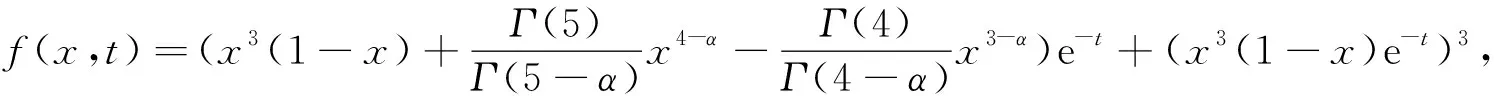
表2 T=1,Δt=10-1,10-2,10-3,10-4,10-5, α=1.2,1.5,1.8,N=4時的L2誤差Tab.2 The L2 error to example 2 at T=1 for different α and Δt with N=4

為了進一步測試算法的可靠性,我們對非線性分數(shù)階Klein-Gordon方程利用提出的數(shù)值格式作了測試．由于問題是非線性的,計算時間較長,所以數(shù)值結(jié)果中的時間步長只取到Δt=10-4,結(jié)果見表 3和表 4．

表3 T=1,Δt=10-4,α=1.2,1.5,1.8,N=3,4時的L2誤差Tab.3 The L2 error to example 3 at T=1 for different α and N with Δt=10-4

表4 T=1,Δt=10-1,10-2, 10-3,10-4,α=1.2,1.5,1.8,N=4時的L2誤差Tab.4 The L2 error to example 3 at T=1 for different α and Δt with N=4

5 結(jié) 論

本文利用Caputo分數(shù)階導(dǎo)數(shù)的特點以及正交多項式的良好性質(zhì),提出了時間用有限差分,空間用移位Legendre正交多項式來逼近求解空間分數(shù)階Klein-Gordon方程的算法．得到的數(shù)值格式簡單,編程實現(xiàn)容易．運用較低的多項式次數(shù)就得到了對解很好的逼近．從算法的推導(dǎo)可以看出,該算法可以推廣到二維和三維情形．文中給出的數(shù)值算例驗證了上述算法的有效性和可行性．

[1] Kusnezov D,Bulgac A,Dang G.Quantum levy processes and fractional kinetics[J].Physical Re-view Letters,1999,82(6):1136-1139.

[2] Mainardi F.Fractional relaxation-oscillation and fractional diffusion-wave phenomena[J].Chaos Solitons Fractals,1996,7(9):20-31.

[3] Ichise M,Nagayanagi Y,Kojima T.An analog simulation of non-integer order transfer functions for analysis of electrode processes[J].J Electroanal Chem Interfacial Electrochem,1971,33:253-265.

[4] Sun H,Abdelwahab A,Onaral B.Linear approximation of transfer function with a pole of fractional power[J].IEEE Transactions on Automatic Control,1984,29(5):441-444.

[5] Cole K.Electric conductance of biological systems[J].Cold Spring Harb Symp Quant Biol,1933,1:107-116.

[6] Mainardi F.Fractional calculus:some basic problems in continuum and statistical mechanics[J].Course and Lectures-international Centre for Mechanical Sciences,1997,378:291-348.

[7] Rossikhin Y,Shitikova M.Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids[J].Applied Mechanics Reviews,1997,50:15-67.

[8] Deng W.Generalized synchronization in fractional order systems[J].Physical Review E,2007,75(5):1-7.

[9] He J H.Approximate analytical solution for seepage flow with fractional derivatives in porous media[J].Computer Methods in Applied Mechanics and Engineering,1998,167(1):57-68.

[10] El-Sayed A M A,Elsaid A,Hammad D.A reliable treatment of homotopy perturbation method for solving the nonlinear Klein-Gordon equation of arbitrary (fractional) orders[J].Journal of Applied Mathematics,2012,2012:1-13.

[11] Sweilam N H,Khader M M,Al-Bar R F.Numerical studies for a multi-order fractional differential equation[J].Physics Letters A,2007,371:26-33.

[12] Jafari H,Daftardar-Gejji V.Solving linear and nonlinear fractional diffusion and wave equations by ADM[J].Appl Math and Comput,2006,180:488-497.

[13] Hashim I,Abdulaziz O,Momani S.Homotopy analysis method for fractional IVPs[J].Commun Nonlinear Sci Numer Simul,2009,14:674-684.

[14] Lin Y M,Xu C J.Finite difference/spectral approximation for the time fractional diffusion equations[J].J Comp Physics,2007,2(3):1533-1552.

[15] Li X J,Xu C J.A space-time spectral method for the time fractional diffusion equation[J].SIAM J Numer Anal,2009,47:2108-2131.

[16] Wazwaz A M.Compacton solitons and periodic solutions for some forms of nonlinear Klein-Gordon equations[J].Chaos,Solitons and Fractals,2006,28(4):1005-1013.

[17] Li S,Vu-Quoc L.Finite difference calculus invariant structure of a class of algorithms for the nonlinear Klein-Gordon equation[J].SIAM Journal on Numerical Analysis,1995,32(6):1839-1875.

[18] Bao W,Dong X.Analysis and comparison of numerical methods for the Klein-Gordon equation in the nonrelativistic limit regime[J].Numerische Mathematik,2012,120(2):189-229.

[19] 陳一鳴,孫慧,劉樂春,等.Legendre 多項式求解變系數(shù)的分數(shù)階Fredholm積分微分方程[J].山東大學(xué)學(xué)報:理學(xué)版,2013,48(6):80-86.

[20] Diethelm K.The analysis of fractional differential equations:an application-oriented exposi-tion using differential operators of Caputo type[M].Berlin:Springer,2010.