基于傅里葉變換和梯度法構建紙張勻度評價模型

徐永建 王 倩 梁巧萍 楊保宏

(陜西科技大學輕工與能源學院，陜西省造紙技術及特種紙品開發重點實驗室，陜西西安，710021)

紙張勻度通常用來描述紙張中纖維及其他固體物質 (如填料等)分布相對均勻的情況，即在一定面積上纖維組成的分布情況［1］，是影響紙張印刷適性、浸漬和涂布適應性、機械強度的重要因素。然而，至今國際上仍未有一種很好的紙張勻度評價體系和測量方法。

紙張勻度的檢測通常分為目測法和儀器法。目測法是在均勻的光線照射下，通過眼睛迎光透視紙張來檢查紙張勻度，檢查的結果不能用數字來表示，需要與一定勻度的標準紙樣進行對比或依靠觀察者的經驗來評判結果［2］。這種評價方法比較主觀，很大程度上取決于觀測者的技術和經驗，誤差大。儀器法主要分為3類:β-射線透射式、β-射線照相法和光透射式［1］。儀器法測量具有較高的準確性和實用價值，可是儀器操作復雜、價格昂貴，尚未普及。

目前隨著數字圖像技術的快速發展，許多研究者采用數字圖像技術對紙張勻度進行檢測，如標準勻度指數表征［3］、梯度法表征［4］、Jordan 比周長法表征［5-6］、區域離散系數表征［7］、傅里葉變換［3］以及小波變換［8］等勻度表征法。其中，傅里葉變換勻度表征根據定量信息在空間的分布來反映紙張勻度，該模型既考慮了纖維具有不同的空間頻域又考慮到其具有不同的幅度，從整體上反映了紙張勻度特征，但此方法無法分析纖維的隨機特征及紙張局部定量的微弱變化。梯度法則從紙張局部定量的微弱變化和紙張整體定量的變化情況反映了紙張勻度特征，是一種很好的勻度分析方法，但在采樣過程中未考慮噪音對圖像質量的影響，對結果的準確度產生了一定的誤差，但這些噪音無法在空間域處理。基于此，本課題采用傅里葉變換將圖像從“空域”變換到“頻域”，在頻域中對圖像進行濾波處理，去除采樣過程中噪音對圖像質量的影響;再利用傅里葉逆變換將圖像從“頻域”變換到“空域”，得到去噪后的勻度圖像;最后利用梯度法構建紙張勻度的評價模型，并將該模型與國際上通用的標準勻度指數表征及視覺評價結果進行對比分析，為紙張勻度分析和評判提供了理論依據。

1 構建評價勻度指數的數學模型

根據Kubelka-Munk理論分析紙張光學性質，當采樣條件一定時，可以確定紙張定量與圖像灰度值之間的關系。攝像機采集的灰度圖像，其各像素點的灰度值與照射到攝像頭光敏面的光通量成一定比例。因此，可以使用灰度值代替紙張局部定量反映紙張勻度信息，建立紙張勻度評價模型。對于紙張光透視圖像來說，某像素點處的光通量越強，透光率則越高，該點處的灰度值就越高，紙張的定量則越小;反之，情況則相反［8］。

圖1 紙張勻度圖像

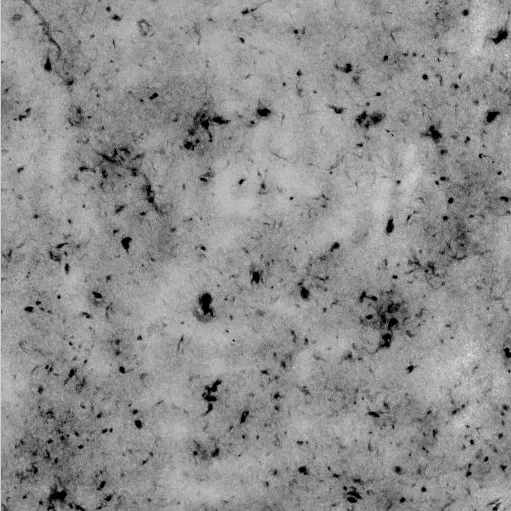
圖2 紙張灰度圖像

圖3 紙張傅里葉頻譜圖

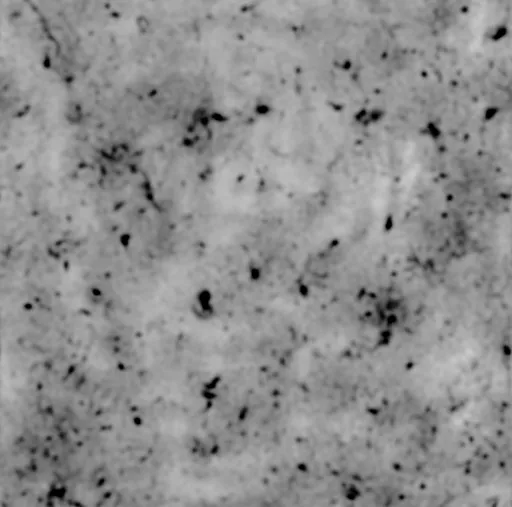
圖4 紙張濾波后的圖像

大量實驗研究發現，攝像機拍攝得到的圖像受離散脈沖、椒鹽噪聲和零均值的高斯噪聲影響較為嚴重。噪聲給圖像處理帶來很多困難，對圖像分割、特征提取、圖像識別等具有直接影響。因此，對實時采集的圖像進行濾波處理是精確計算紙張勻度的關鍵。如果直接在時域進行濾波處理，計算量會隨采樣點數的平方而增加，這使得計算機處理時計算量大、費時，很難達到實時處理的要求。相比于時域中的信號，計算機更易處理頻域中的信號，且處理速度更快、計算量更小，因此，筆者使用傅里葉變換完成圖像在“時域”和“頻域”之間的轉換，將不宜或無法在空域中處理的一些特征信息轉換到頻域中進行處理。根據資料記載［9］，數字圖像中的邊緣和噪聲對應于傅里葉變換中的高頻部分，所以若在頻域中消弱其影響就要設法減弱高頻部分的分量。由于巴特沃斯低通濾波器在高低頻率間的過渡比較光滑，輸出圖像中的振鈴現象不明顯。因此，使用巴特沃斯低通濾波器消除了傅里葉變換中的高頻分量，去除了圖像中的噪音，其中巴特沃斯低通濾波器的傳遞函數見公式 (1)［9］。紙張勻度圖像經傅里葉變換濾波后的效果圖見圖1～圖4。

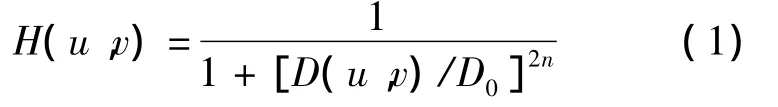
式中，u為0，1，…，M －1;v為0，1，…，N －1;D(u，v)為從點(u，v)到頻率平面原點的距離，D0為截止頻率。

采用傅里葉濾波后的勻度圖像，筆者采用梯度法［4］構建紙張勻度的數學模型，見公式 (2)。在梯度法分析中，有兩個參數值得注意:平均梯度和均方差。平均梯度是指圖像的邊界或影線兩側附近灰度有明顯差異，即灰度的變化率，是各像素點梯度值的數學統計，反映了圖像微小細節反差變化的速率，即圖像在多維方向上局部定量的微觀變化情況。平均梯度越小，紙張局部定量變化越小，紙張勻度越好;反之，情況則相反。在平均梯度分析中，有研究者［4］發現為了減少計算機的計算量，使用Roberts交叉差分算法代替微分處理的結果優于典型差分法處理的結果。均方差反映了局部定量與整體的偏離程度，均方差小說明紙張定量比較均勻［10］，勻度較好;均方差大，表明紙張勻度差。因此，梯度指數既反映了紙張局部定量的微弱變化，又反映了整體定量的變化情況，較全面地反映了紙張勻度信息。

圖5 隨機抽取的不同勻度紙樣的灰度圖像

式中，σ為紙張局部定量的均方差;FGN為梯度指數;為采樣圖像的平均梯度。

2 實驗研究及分析

本實驗的勻度分析，采用隨機抽取的幾種不同勻度的紙樣作為分析紙樣 (灰度圖像見圖5)，評價構建勻度指數的數學模型。其中，采集圖像所使用的光源為D65，攝像頭參數為AF-S DX 18～55 mm f/3.5-5.6G ED II，紙樣大小為8 cm×8 cm，有效分辨率為256像素/cm，經攝像頭得到的勻度圖像采用Matlab軟件進行處理。分別采用標準勻度指數［3］和本實驗所構建的勻度指數模型計算紙張勻度，為了對比此模型的性能及優勢，同時筆者也采用視覺評價分析上述紙樣，即選定17個人對不同勻度的紙樣進行評價，這些人來自陜西科技大學制漿造紙工程專業，具備正常的視覺觀測;此外，在評價前需對這些人如何采用視覺觀測評價紙張勻度進行相關培訓。勻度指數模型及視覺評價結果見表1。為了更進一步比較該模型與標準勻度模型的區別，筆者取兩張紋理不同(紙樣G和H)但勻度指數相同的兩幅圖像進一步分析 (見圖6)，其分析結果見表2。

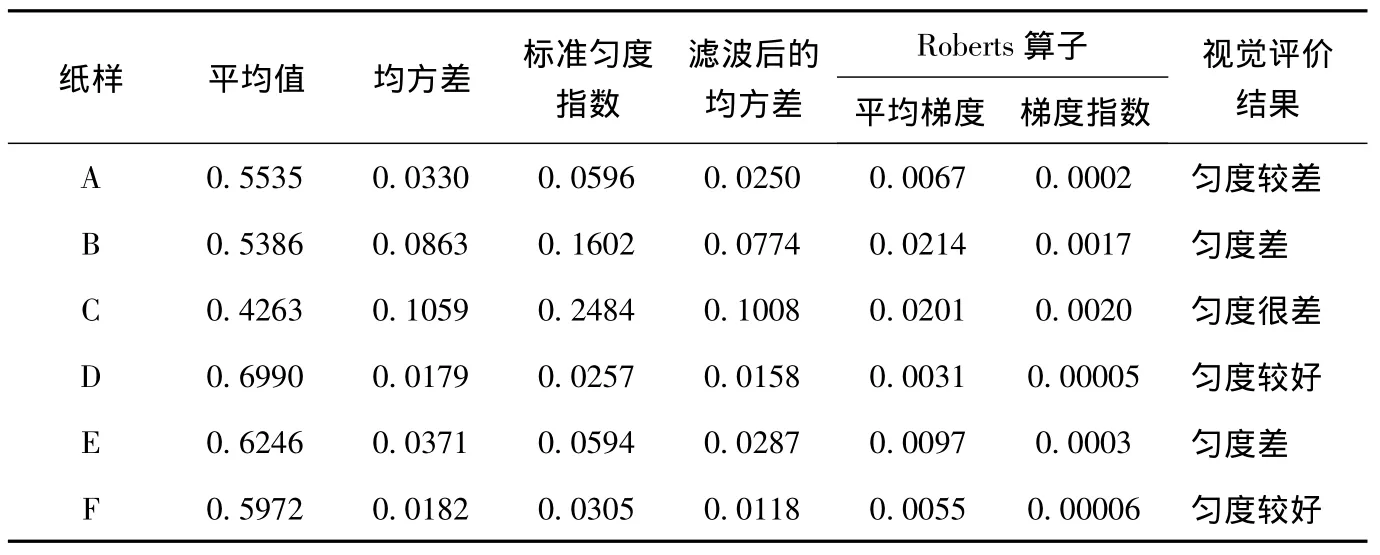
表1 勻度指數模型及視覺評價結果

表2 兩種模型對紙樣G和H的分析評價結果

在數字圖像處理的過程中，筆者常采用均一化處理，將數據單位化，使得所有數據都歸化為0～1。采用歸一化的好處是簡便、準確、定量結果與采樣量重復性無關，操作條件略有變動或采樣量控制不十分準確對分析結果影響都很小，因此，本實驗對上述所采用的幾種方法都采用了均一化處理。

由表1可知，梯度指數越小，紙張勻度越好。采用傅里葉變換濾波處理的紙張，在頻域中濾波后，高頻部分的噪音減少，使得勻度圖像中灰度值的均方差變小。采用視覺觀測評價不同種類、不同定量的紙張時，其結果對比性不強，誤差較大，不能直接用數值表示;而數字圖像處理則輕松地解決了此問題，可以將不同種類、不同定量的紙張進行對比分析，應用范圍更廣。由表1梯度指數和標準勻度指數可知，兩種方法處理結果的趨勢一致。由圖6可知，G紙樣絮聚團較多，分布不均勻，H紙樣的勻度較好。由表2知，利用標準勻度算法處理G和H紙樣時，卻得到了相同的結果，而本實驗所構建的勻度評價模型不僅從整體上反映了紙張的勻度特征，同時還考慮了紙張局部定量的微弱變化，可以很容易地將紙張的勻度信息放大分析，與視覺評價結果和標準勻度指數模型所得到的結果均有很好的相關性，且得到與視覺評價更接近的結果，因此，本實驗所構建的模型更具有優勢，更加全面地反應了紙張勻度信息。

圖6 紙樣G和H的灰度圖像

4 結論

針對紙張勻度問題，采用傅里葉變換，將不易在空間域處理的信息轉換到頻域，有效地去除了圖像中的噪音，并結合梯度法構建了紙張勻度的評價模型，既反映了紙張局部定量的微弱變化，又反映了整體定量的變化情況，較全面地反映了紙張勻度信息，提高了紙張勻度分析時的精度。該方法與標準勻度指數及人眼視覺評價結果均有很好的相關性。另外，采用數字圖像處理思路簡單，實現方便，為紙張勻度的分析和評判提供了一些理論依據。

［1］ Lu Qianhe．Papermaking Principle and Engineering［M］．Beijing:China Light Industry Press，2008．盧謙和．造紙原理與工程［M］．北京:中國輕工業出版社，2008．

［2］ Zhang Lijiu，Chen Yanqing．Theories and Methods of Testing Paper Formation［J］．Shanghai Paper Making，1984(Z1):52．張立九，陳延慶．紙張勻度測試的理論與方法［J］．上海造紙，1984(Z1):52．

［3］ YAN Dong-bo，LIU Huan-bin．Characterization of Sheet Formation［J］．China Pulp ＆ Paper，1997，16(6):6．閻東波，劉煥彬．紙頁勻度的一種表征方法［J］．中國造紙，1997，16(6):6．

［4］ Ji Hongyan，Wang Yongxiu，Fan Qiuhua．Method for Detecting Paper Formation by Using Computer Vision［J］．Journal of Qingdao University Engineering＆ Technology Edition，2003，18(1):35．季鴻雁，王永秀，范秋華．一種計算機視覺紙張勻度檢測方法［J］．青島大學學報，2003，18(1):35．

［5］ Jordan B D，Nguyen N G．Specific perimeter，a graininess parameter for formation of print mottle textures［J］．Pulp＆ Paper Research Institute of Canada，1986，6(7):476．

［6］ Jordan B D，Nguyen N G．Specific perimeter:a statistic for assessing，formation and print quality by image analysis［J］．Tappi Journal，1998，81(10):191．

［7］ Chang Faliang，Wang Ping，Qiao Yizheng，et al．Advanced Gradient Index Analysis Method for the Evenness Based on Computer Vision and Its Application［J］． Controland Decision， 2004， 19(10):1125．常發亮，王 平，喬宜正，等．視覺勻度分析的改進梯度指數法及其應用［J］．決策與控制，2004，19(10):1125．

［8］ Qiu Shubo．Research on Detecting Method for Pulp Fibre and Paper Sheet Quality Based on Image Analysis Technology［D］．Tianjin University，2006．邱書波．基于圖像分析技術的紙漿纖維與紙張質量檢測方法研究［D］．天津:天津大學，2006．

［9］ Yao Min．Digital image processing［M］．Beijing:China Machine Press，2006．姚 敏．數字圖像處理［M］．北京:機械工業出版社，2006．

［10］ Sun Jingjuan．Statistics［M］．Beijing:Tsinghua University Press，2006．孫靜娟．統計學［M］．北京:清華大學出版社，2006．CPP