擺動式橫切剪運動學仿真分析及剪刃側隙補償研究

董義君 劉小丹 陶有能 嚴國平 嚴 淑

(1:中冶南方工程技術有限公司 湖北武漢430223；2:武漢凱比思電力設備有限公司 湖北武漢430223)

擺動式橫切剪運動學仿真分析及剪刃側隙補償研究

董義君①1劉小丹2陶有能1嚴國平1嚴 淑1

(1:中冶南方工程技術有限公司 湖北武漢430223；2:武漢凱比思電力設備有限公司 湖北武漢430223)

闡述了擺動式橫切剪的剪切機構，分析剪切過程并提取其運動學模型，通過對剪刃側隙的分析，建立了補償模型。通過運動學仿真分析繪制了剪刃側隙補償曲線。研究結果表明，按照剪刃側隙為0進行補償，其補償曲線具有通用性，能夠滿足不同規格帶鋼對剪刃側隙的調整要求。

擺動式橫切剪 運動學 剪刃側隙 補償

1 引言

擺動式橫切剪在帶鋼連續生產線上應用前景廣泛，可對帶鋼進行切頭、切尾或定尺剪切。剪切后的帶鋼直接進入焊機或作為成品卷包裝。因此，對剪切斷面質量要求高，斷面必須平直、整齊。一些學者對剪切機構進行了大量分析和仿真計算。楊春青等[1]對斜刀片剪切機剪切力進行了分析；尤敏等[2]對雙層剪剪切力、剪刃側隙調整機構進行了分析；陳潔[3]采用運動閉環矢量方程對曲柄搖桿式飛剪的剪刃側隙進行了運動學分析。這些文章主要對斜刀片剪切機、飛剪等剪切機的剪切力、側隙調整和運動學進行計算和分析。鄧亨速等[4]對液壓擺式剪板機的幾何參數進行了計算，其剪切對象為熱軋厚板，剪切質量要求不高，剪刃側隙不需要補償。

擺動式橫切剪用于剪切冷軋薄帶鋼，對剪刃側隙要求高，是近兩年研發出的新機型，未見涉及該機型的論文與報道。

2 運動學模型

2.1 剪切過程

擺動式橫切剪的特點是下剪刃固定不動，上剪刃繞固定鉸點擺動(該“固定鉸點”位置可調，通過偏心軸調整好剪刃側隙后，固定偏心軸以固定該鉸點位置)。剪切動作由上剪刃來完成，剪切機構為多桿機構。

下剪刃為矩形平剪刃，上剪刃為V形剪刃，如圖1所示。下剪刃安裝在機架上，固定不動；上剪刃安裝在上刀架上，通過多桿機構擺動，擺動軌跡為一段弧線，如圖中雙點劃線所示軌跡線。剪刃從兩端A1、O1首先進入剪切，依次為點A2、O2，一直到剪刃中間點An、On。多桿機構擺動到下極限位時，完成剪切。上剪刃沿原軌跡線返回，到達上極限位，即剪切準備位，準備下一次剪切動作。

從剪切原理可以看出，上、下剪刃從A1、O1，A2、O2……到An、On，即從剪刃的兩端往中間依次進入剪切，剪切區域小且為連續剪切，剪切力小，可有效減輕設備重量；左右對稱，受力均勻平衡，受力好。

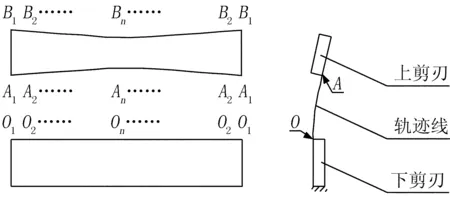
圖1 上、下剪刃示意圖

2.2 運動學模型

為求得剪切過程中上、下剪刃側隙的變化，必須建立擺動式橫切剪的運動學模型。

如圖2所示，該多桿機構由桿1、桿2、桿3、桿4、油缸5及固定機架6(機架未示出)組成。通過調整桿1的角度，設定上剪刃在擺動過程中的某一時刻，上剪刃中點An與下剪刃中點On重合(圖1)，該點作為本文中闡述的剪刃側隙補償的基準點，然后固定桿1；上剪刃安裝在桿2上，隨桿2的擺動而擺動；下剪刃安裝在機架6上，固定不動；桿3為連桿；桿4為擺動桿，其中間為一固定鉸點，圖中雙點劃線示出桿4右端點軌跡線；油缸5最短行程時，對應上剪刃上極限位，為剪切準備位；最長行程時，對應上剪刃下極限位，為剪切完成位。

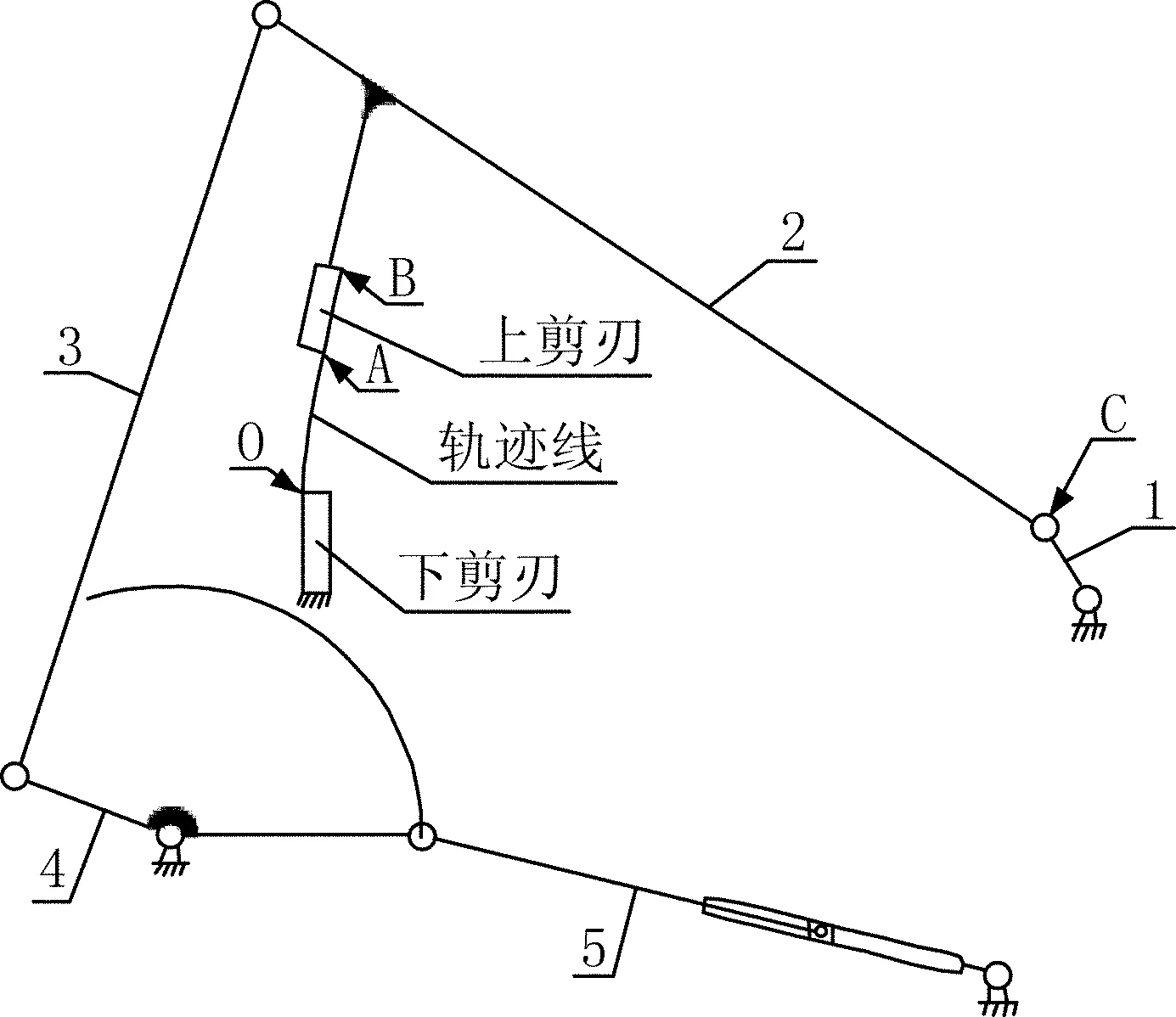
圖2 擺動式橫切剪運動學模型

3 剪刃側隙補償

剪刃側隙、重疊量及刃口狀態等對剪切質量都有影響，剪刃側隙是起決定性作的[5]。

從圖2可以看出，上剪刃隨桿2一起繞固定鉸點C擺動，圖中雙點劃線示出上剪刃剪切點A的軌跡線。該軌跡線表明，桿2擺動中，上、下剪刃對應的剪切點A、O有逐漸遠離的趨勢。以上、下剪刃An、On重合作為補償基準，則上剪刃A1、A2……An-1對應下剪刃O1、O2……On-1在剪切過程中會發生干涉。

因此，為保證剪切過程中上、下剪刃相對剪切點之間的剪刃側隙的不變，必須對剪刃的側隙進行補償。

3.1 補償模型

補償的原理是保證剪切過程中上、下剪刃剪切對應點之間的距離不變，即剪刃側隙不發生改變。

如圖3所示，取剪切行程任一位置，上、下剪刃的相對位置圖。在下剪刃剪切點O建立坐標系，X軸水平往右，Y軸豎直向上。

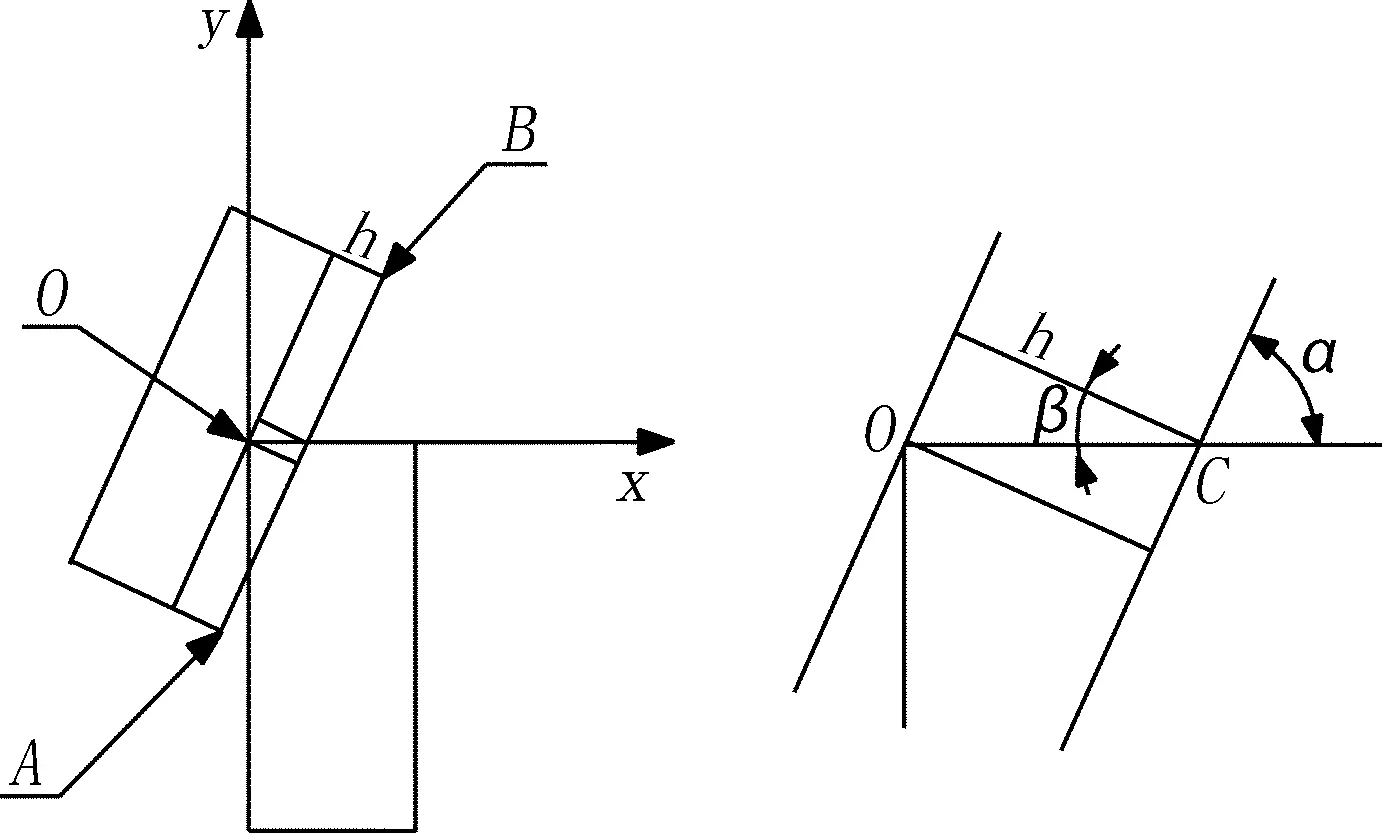
圖3 補償模型

下剪刃剪切點O(0，0)，與坐標原點重合。上剪刃面向下剪刃一側剪切面建立A(x1，y1)，B(x2，y2)，過O做垂直與AB的輔助線，輔助線長度為h，則在該剪切位，上剪刃的補償量為h。

圖3右圖，為左圖的剪切點局部放大圖。直線AB與x軸相交于點C(x3，0)。

直線AB的直線方程公式為：

(1)

直線AB與x軸交點C(x3，0)，令(1)式中y=0，則：

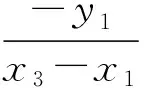
(2)

整理上式，則：

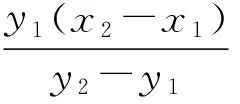
(3)

根據直角三角形邊角關系，有：

h=OC×cosβ=x3×cosβ

(4)

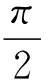
(5)

根據直線方程斜率公式，有：

(6)

將式(3)、(5)、(6)帶入式(4)，則：

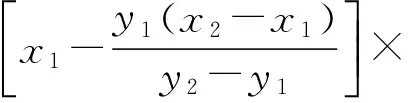
(7)

化簡上式，則：

(8)

剪切判據：

x1≤0≤x2

(9)

y1≤0≤y2

(10)

由(9)、(10)兩式判斷上、下剪刃是否進入剪切。未進入剪切時，不需要進行剪刃補償；進入剪切時，根據式(8)可以算出補償量。

補償后的上剪刃，在整個剪切過程中，可以實現上、下剪刃側隙為0。

3.2 補償曲線

運動學仿真是指利用仿真軟件包反復求解機構運動約束方程，通過積分獲得最終的速度(或加速度)，從而確定機構運動的位置(和速度)。這樣，一個軟件包與通常求解機構運動的方法相比具有許多優點，其中最顯著的優點是位置問題可以用軟件包隱式求解，使用者只需為仿真包提供適當的初始條件即可以求解機構在任意時刻的位置(和速度)問題。

如圖2 所示，驅動油缸5從最短極限位伸長至最長極限位，再由最長極限位縮短至最短極限位，完成一次剪切動作。

如圖4所示，通過運動學仿真分析，可求得任一剪切點處，上剪刃上點A、點B的坐標。帶入式(8)，可求得該點的補償值h的大小。

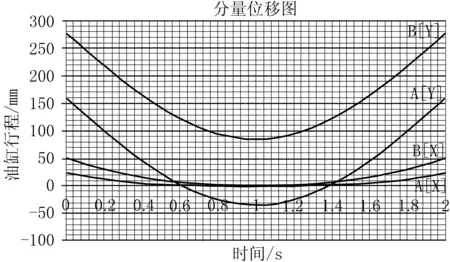
圖4 分量位移圖

通過對全剪切過程中剪切點的補償值計算，可求出上剪刃的補償曲線。如圖5所示，因全剪刃長度關于中間平面對稱，本圖顯示為上剪刃1/2補償模型。其補償值為0.00mm數量級，為能看出補償曲線規律，本圖中補償曲線采用了夸張畫法。

因上剪刃為V形刀刃，且剪切一定次數后刃口鈍化需要重新修磨，剪刃結構必須簡單易于制造及修磨。所以，在上機架安裝上剪刃側按照補償曲線加工型面(補償曲線)，上剪刃通過螺栓組固定安裝在上刀架上，合理布置螺栓組間距，可在上剪刃剪切面再現補償曲線。實際計算時，每50mm計算一個補償值，通過樣條曲線將所有補償值連接起來形成補償曲線。

圖5 補償曲線示意圖

實踐證明，按照50mm計算一個補償值，且將補償曲線加工在上機架剪刃側，上剪刃通過螺栓組固定安裝在上刀架補償曲線型面上，可以達到剪切要求，剪切質量好，斷面平直、整齊，滿足工藝要求。

4 補償曲線通用性分析

對剪刃側隙為0mm的情況，進行了補償分析。實際使用時生產線須滿足不同規格鋼板的剪切需求。不同帶鋼對應不同的剪刃側隙，因此需對該補償曲線的橫切剪對應不同規格鋼板的剪切的通用性進行分析。

如圖6所示，分析了剪刃側隙為0mm、0.25mm、2mm時補償曲線的變化規律及數值。分析表明，不同剪刃側隙對補償曲線的影響數量級為0.000mm，小于補償曲線0.00mm的數量級，因此該補償曲線能夠滿足不同剪刃側隙的補償要求。

b)側隙為0.25mm

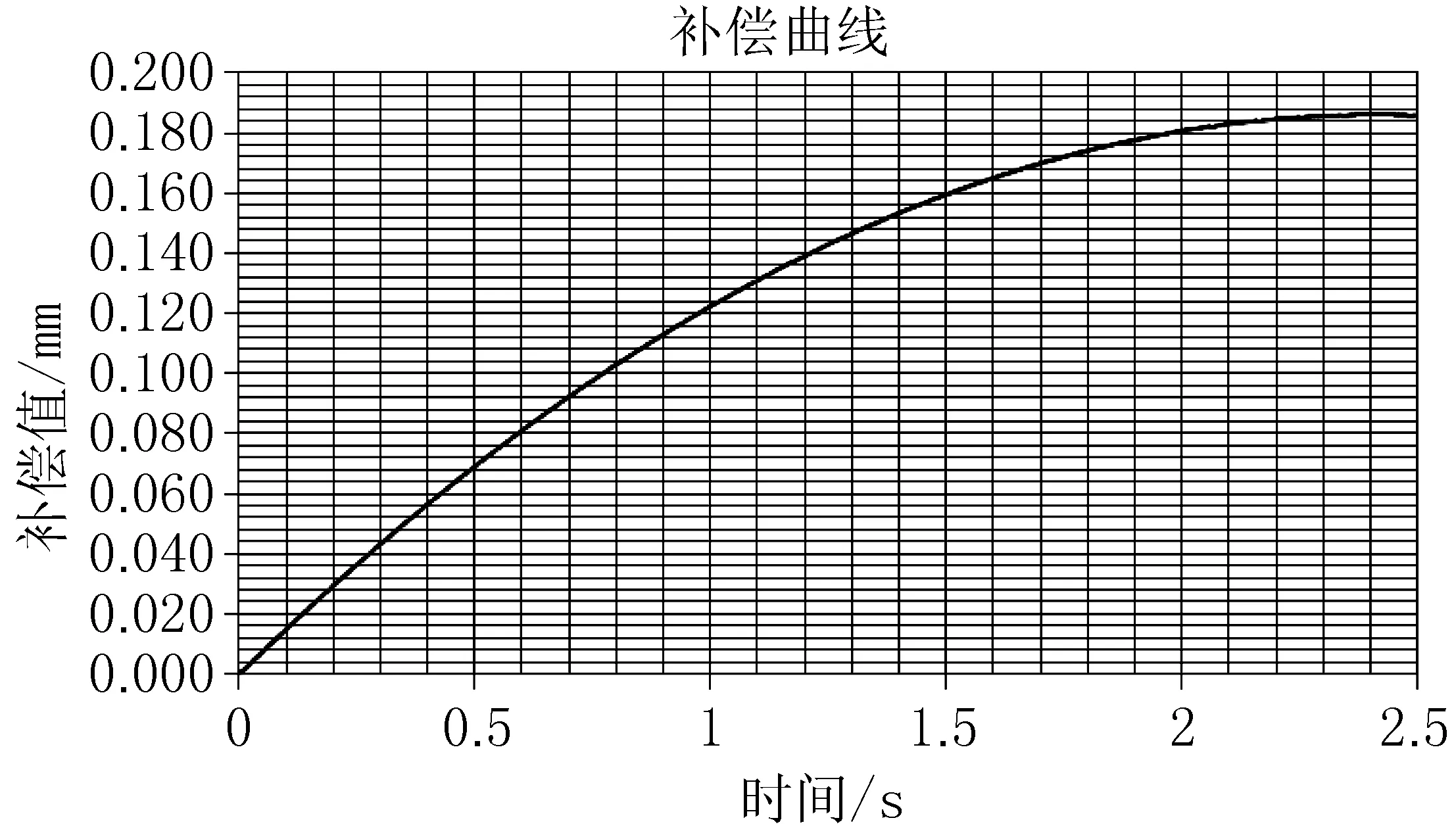
c)側隙為2mm圖6 補償曲線通用性分析

只需要調整圖2中桿1的角度，即可獲得大小可調且全剪切過程中大小一致的剪刃側隙值。

5 結論

提取了擺動式橫切剪的運動學模型，并建立了剪刃側隙補償算法，通過運動仿真分析，獲得了剪刃側隙補償值并繪制了補償曲線。

按照剪刃側隙為0mm進行補償，其補償曲線具有通用性，能夠滿足不同規格帶鋼對剪刃側隙的調整要求。

剪刃側隙調整簡單。通過調整偏心軸的角度，可獲得全剪切過程中大小一致的剪刃側隙，剪切斷面質量高。

[1]楊春青等.下切式液壓剪的設計[J].液壓與氣動,2012(8):37-38.

[2]尤敏等.雙層剪的設計與分析[J].冶金設備,2012(6):22-25.

[3]陳潔.曲柄搖桿式飛剪剪刃間隙研究[J].重型機械,2013(1):40-42.

[4]鄧亨速等.擺式剪板機的幾何參數與計算[J].現代機械,1986(1):19-22.

[5]吳志生.冷軋板帶切邊變形過程及其影響因素[J].輕合金加工技術,2001,Vol.29(12):23-24.

[6]陶有能.切邊圓盤剪設計[J].華中科技大學學報(城市科學版),2006,Vol.23(增刊2):77-79.

歡迎投稿 歡迎訂閱 歡迎刊登廣告

Kinematics Simulation Analysis of Swing Crosscut Shear and
Research of Shear Side Clearance Compensation

Dong Yijun1Liu Xiaodan2Tao Youneng1Yan Guoping1Yan Shu1

(1:WISDRI Engineering & Research Corporation Limited, Wuhan 430223; 2:Wuhan Kempinsh Power Equipment Co.,Ltd., Wuhan 430223)

This paper, the shear structure of swing crosscut shear is elaborated, analyzes the cutting course and extracts kinematics model, and builds compensation model through the analysis of shear side clearance. The shear side clearance compensation curve is put forward by analysis of kinematics simulation. The research proves that, the compensation curve is universal on the basis of zero shear side clearance, which can meet the adjusting requirement of shear side clearance for various strip steel.

Swing crosscut shear Kinematics Shear side clearance Compensation

董義君，男，1983年出生，畢業于武漢大學動力與機械學院，碩士，工程師，從事軋鋼設備的研究與設計

TG333.2

A

10.3969/j.issn.1001-1269.2014.04.004

2014-04-22)