CPSO優(yōu)化FLS-SVM應(yīng)用于山區(qū)地形的GPS高程擬合研究
甘 勇, 劉新新,鄭遠(yuǎn)攀
(1. 鄭州輕工業(yè)學(xué)院 計(jì)算機(jī)與通信工程學(xué)院,河南 鄭州 450002; 2. 鄭州師范學(xué)院,河南 鄭州 450044;3. 應(yīng)急平臺信息技術(shù)河南省工程實(shí)驗(yàn)室,河南 鄭州 450002)
一、引 言
目前國內(nèi)應(yīng)用于各種領(lǐng)域的高程數(shù)據(jù)是基于1985 國家高程基準(zhǔn)的正常高,而SRTM則是采用基于EGM96 高程基準(zhǔn)的正高,因此,對高程轉(zhuǎn)換的研究就自然成為SRTM數(shù)據(jù)應(yīng)用的基礎(chǔ)。根據(jù)研究可知,大地高與正常高間的關(guān)系表示為:H大=H正+ξ=H正常+N。其中,H大表示大地高;H正表示正高;ξ表示大地高與正高之間的高程異常。除數(shù)據(jù)本身大地高測量誤差外,高程異常是制約正常高精度的關(guān)鍵。
求解高程異常的常用方法主要是利用GPS聯(lián)測方法來擬合高程獲得的。傳統(tǒng)的求解方法主要有多項(xiàng)式擬合法、曲面擬合法、多面函數(shù)擬合法[1]等。由于這些方法都存在不同程度的人為參與,影響了模型的精度,近年來一些學(xué)者基于原有理論基礎(chǔ)提出了基于神經(jīng)網(wǎng)絡(luò)及其改進(jìn)算法[2-3]的高程擬合算法、支持向量機(jī)等算法。神經(jīng)網(wǎng)絡(luò)算法的應(yīng)用雖然模型簡單、易學(xué)習(xí),但算法收斂速度慢,易陷入局部最優(yōu);雖然有學(xué)者也作了改進(jìn),消除了局部最優(yōu)狀態(tài),但整體擬合精度沒有顯著提高。1995年基于結(jié)構(gòu)風(fēng)險(xiǎn)最小化的支持向量機(jī)模型[4-5]的首次出現(xiàn)受到了眾多學(xué)者的關(guān)注,它不僅在解決小樣本、非線性及高維模式識別中表現(xiàn)出許多特有的優(yōu)勢,同時(shí)克服了神經(jīng)網(wǎng)絡(luò)過擬合、局部最優(yōu)等問題,是繼神經(jīng)網(wǎng)絡(luò)之后的又一研究熱點(diǎn)。
周理含[6]將最小二乘支持向量機(jī)(LS-SVM)引入GPS高程擬合領(lǐng)域,簡化了計(jì)算復(fù)雜度,提高了擬合速度,但向量機(jī)參數(shù)的選擇存在人為的不確定性。湯凱煌[7]考慮了山區(qū)地形起伏對擬合精度的影響,提出基于地形改正的GPS高程異常曲面擬合方法,雖然減小了因地形起伏引起的精度影響,但曲面擬合方法適用于樣本數(shù)據(jù)較大的情況,對于較小樣本擬合精確度較低。
本文在眾多學(xué)者研究結(jié)果的基礎(chǔ)上提出一種應(yīng)用于地形起伏較大山區(qū)的考慮地形改正在內(nèi)的CPSO優(yōu)化FLS-SVM的GPS高程擬合方法。該方法引入模糊思想構(gòu)成模糊最小支持向量機(jī)模型(FLS-SVM),通過CPSO優(yōu)化選擇核函數(shù)參數(shù),可減少人為參數(shù)選擇不確定性對精度的影響,并通過地形改正減少地形起伏引起的精度降低情況。
二、最小二乘支持向量機(jī)原理及模糊理論的引入
最小二乘支持向量機(jī)[6-8]是在1999年由Suyken和Smola正式提出的基于SVM改進(jìn)的一種模型。它承接了支持向量機(jī)訓(xùn)練過程中結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則,采用等式約束代替不等式約束作為損失函數(shù),代替?zhèn)鹘y(tǒng)支持向量機(jī)中的二次規(guī)劃方法,解決了SVM 在樣本數(shù)目多時(shí)計(jì)算速度慢、復(fù)雜、收斂精度低等二次規(guī)劃問題。
給定一個(gè)有M個(gè)訓(xùn)練樣本的數(shù)據(jù){(xi,yi),i=1,2,…,M}表示n維向量,且(xi,yi)∈Rn×R,其中xi為樣本輸入數(shù)據(jù),yi為樣本輸出數(shù)據(jù)。通過非線性映射,將輸入數(shù)據(jù)向量空間映射到高維特征輸出數(shù)據(jù)向量空間構(gòu)建最優(yōu)超平面。根據(jù)結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則,最小二乘支持向量機(jī)的最優(yōu)表示函數(shù)為
式中,目標(biāo)函數(shù)的兩項(xiàng)分別表示模型的泛化能力和精確度;w為權(quán)向量;ξi為模型松弛因子;b為模型偏差;γ為可調(diào)參數(shù),可調(diào)節(jié)控制J(w,ξ)函數(shù)。引入Lagrange函數(shù)乘子αi(i=1,2,…,n)后的等式約束目標(biāo)函數(shù)為

由KKT等式條件,上述函數(shù)求解可得
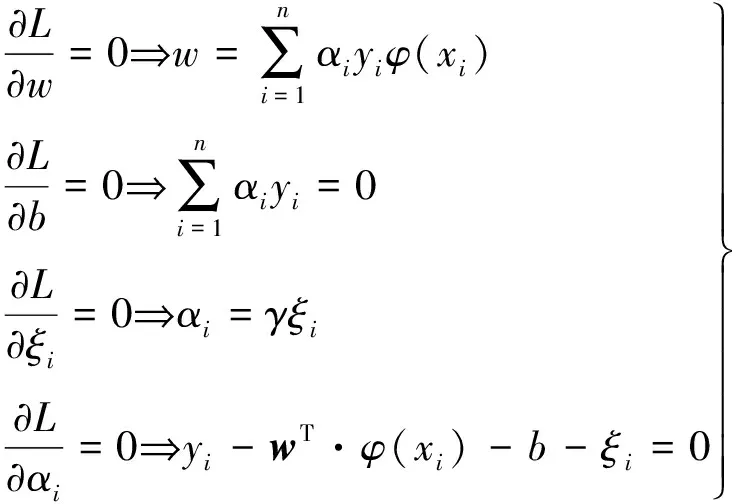
消去變量w和ξi,可得方程組
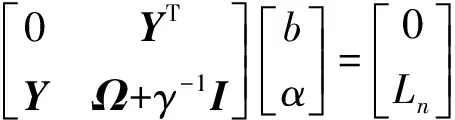
式中,Ω=[Ωi,j]n×n是一個(gè)n階對稱矩陣。根據(jù)Mercer條件,可知Ωi,j=yiyjφ(xi)Tφ(yj),又根據(jù)核函數(shù)K(xi,xj)=φ(xi)Tφ(xj),即可將目標(biāo)函數(shù)轉(zhuǎn)化為最小二乘支持向量機(jī)非線性模型

由上可知,正則化參數(shù)γ和核參數(shù)σ的確定是影響LS-SVM模型計(jì)算的基礎(chǔ)。同時(shí)為解決LS-SVM對于孤立點(diǎn)過于敏感的問題,將模糊思想[10]引入到LS-SVM中,對樣本進(jìn)行模糊化處理,即為每個(gè)樣本引入模糊隸屬度μi,則目標(biāo)函數(shù)模型方程組表示為
由此可知,引入模糊思想的LS-SVM模型中模糊隸屬度即表示了樣本對回歸擬合貢獻(xiàn)的程度,是影響模型精度的因素之一。
三、山區(qū)局部地形改正方法
傳統(tǒng)的高程擬合方法[3]只適用于高程異常變化較小的平緩地區(qū),不適用于高程異常變化劇烈的山區(qū)地帶。本文考慮到地形起伏對高程擬合精度的影響,將局部地形改正方法應(yīng)用于地形起伏較大的山區(qū)地帶,奠定了后期高程擬合的基礎(chǔ)。
由于高程受到地球重力場模型、平均重力異常和數(shù)字高程模型的影響[11],將高程異常影響因素表示為
ξ=ξGM+ξΔg+ξTC
式中,目標(biāo)函數(shù)項(xiàng)分別表示為重力場模型、重力異常和地形起伏對高程的影響。如果以20 km波長為界來考慮,高程異常可表示為
ξ=ξ0+ξTC
式中,ξ0和ξTC分別表示高程異常的中長波項(xiàng)和短波項(xiàng)。中長波項(xiàng)由重力場模型和重力異常構(gòu)成,一般較為穩(wěn)定,可忽略不計(jì),短波項(xiàng)是由地形起伏引起的,因此需要對地形進(jìn)行局部改正。將周圍地形起伏點(diǎn)的擾動(dòng)位進(jìn)行疊加求得該點(diǎn)地形起伏對高程異常精度的影響值[11],即
式中,Tc為擾動(dòng)位的影響;r為重力值;r0為格網(wǎng)點(diǎn)和待求點(diǎn)間的距離。
四、混沌粒子群優(yōu)化FLS-LVM參數(shù)的山區(qū)GPS高程擬合
高程擬合模型建立流程圖如圖1所示。
1. 移去局部地形改正
本文根據(jù)“移除-恢復(fù)”法,由SRTM DEM數(shù)據(jù)[7]計(jì)算出參與擬合點(diǎn)的地形改正ξTC。鑒于高程異常值影響因素中的中長波項(xiàng)一般比較穩(wěn)定,對高程異常精度沒有太大影響,本文只考慮短波項(xiàng)的影響,即首先需要移去高程異常值中的短波項(xiàng),即f(x)=ξ-ξTC,獲得預(yù)處理樣本集;然后并對樣本集進(jìn)行有效處理,劃分不同的訓(xùn)練集和測試集組合樣本。
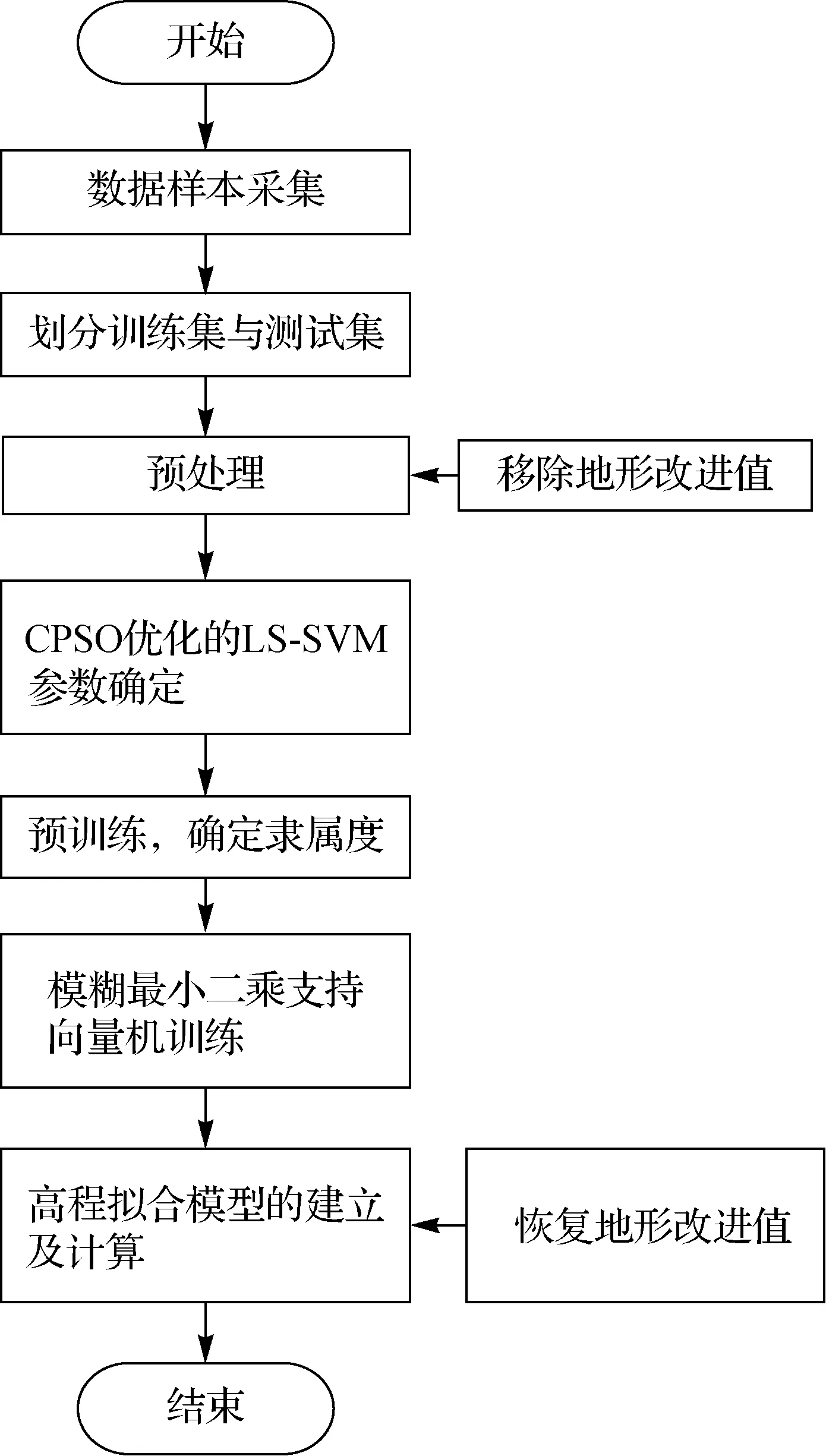
圖1 高程擬合模型流程圖
2. CPSO應(yīng)用于LS-SVM的參數(shù)選擇
LS-SVM作為SVM的一種改進(jìn)模型,也是一種自學(xué)習(xí)算法模型,其性能主要依賴于學(xué)習(xí)機(jī)的參數(shù)選擇,因此,提高其學(xué)習(xí)和泛化能力成為目前LS-SVM應(yīng)用的主要研究問題,正則化參數(shù)γ和核參數(shù)σ是提高模型學(xué)習(xí)和泛化能力的重要指標(biāo)。
目前常用的LS-SVM參數(shù)選擇方法[9]有正交驗(yàn)證法、基于遺傳算法的參數(shù)選擇、基于粒子群算法的參數(shù)選擇。傳統(tǒng)的正交驗(yàn)證法雖然在一定程度上可以獲得較好的泛化能力,但針對大樣本參數(shù)選擇會(huì)增大計(jì)算量;遺傳算法在參數(shù)選擇上具有自動(dòng)性和大樣本收斂速度快的優(yōu)點(diǎn),但存在算法操作復(fù)雜、易早熟收斂,影響了算法的有效性;粒子群優(yōu)化算法雖然減少了遺傳算法中的“交叉”、“變異”操作,算法簡單易實(shí)現(xiàn),收斂速度快,但易遭遇進(jìn)化初期收斂速度快,后期收斂速度慢的收斂問題,從而陷入局部極值問題,并且在計(jì)算過程中還易遭遇維數(shù)災(zāi)難。因此,本文針對傳統(tǒng)參數(shù)選擇方法無法解決的問題提出了一種基于混沌粒子群的最小二乘支持向量機(jī)參數(shù)選擇方法,通過選擇參數(shù)γ和σ的最優(yōu)組合來提高模型的學(xué)習(xí)和泛化能力。參數(shù)選擇流程如下:
1) 對最小二乘支持向量機(jī)參數(shù)進(jìn)行初始化設(shè)置并作歸一化處理,設(shè)置最大迭代次數(shù)。
2) 進(jìn)行混沌空間搜索。
3) 反歸一化計(jì)算最小二乘支持向量機(jī)參數(shù)。
4) 將向量機(jī)模型輸出值同歷史最優(yōu)值進(jìn)行比較,如果當(dāng)前值更優(yōu),則將該值替換原有的歷史最優(yōu)值;否則返回步驟1),重新進(jìn)行計(jì)算。
5) 若滿足迭代次數(shù),輸出搜索最優(yōu)值;否則返回步驟1),重新搜索。
6) 將上述搜索結(jié)果作為粒子群初值,將空間中的每個(gè)粒子和整個(gè)群體中的粒子同歷史最優(yōu)位置進(jìn)行比較,替換原有的歷史最優(yōu)位置并更新最優(yōu)位置新參數(shù)。
7) 新參數(shù)建立新的向量機(jī)模型并輸出模型最優(yōu)值;否則返回步驟6),重新進(jìn)行計(jì)算。
8) 若滿足最終迭代次數(shù),則停止搜索,輸出最優(yōu)向量機(jī)模型參數(shù);否則返回步驟6)繼續(xù)迭代。
3. 樣本模糊隸屬度值的確定
本文根據(jù)上述設(shè)定的訓(xùn)練集和測試集的不同組合樣本,以及經(jīng)過CPSO優(yōu)化獲得的模型參數(shù)進(jìn)行最小二乘向量機(jī)模型預(yù)訓(xùn)練,根據(jù)樣本預(yù)訓(xùn)練輸出值與期望值間的關(guān)系確定隸屬度值。
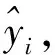
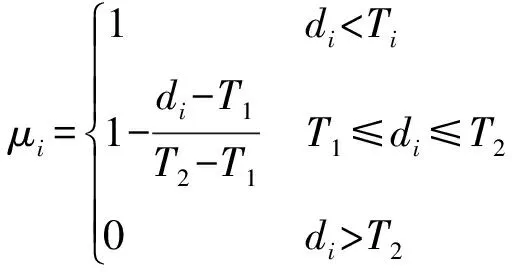
為使訓(xùn)練樣本不受噪聲或異常點(diǎn)的影響,令T1=σ,其中
4. 高程擬合模型建立及應(yīng)用
假設(shè)高程異常為
ξi=Ha(Xi,Yi,Zi)
式中,(Xi,Yi,Zi)分別為GPS水準(zhǔn)點(diǎn)坐標(biāo)中的平面坐標(biāo)和大地高坐標(biāo)。
本文高程擬合模型以GPS水準(zhǔn)點(diǎn)三維坐標(biāo)(Xi,Yi,Zi)作為輸入量,高程異常作為輸出量,構(gòu)成求解高程異常的非線性方程模型。此外,顧及山區(qū)地形起伏對高程異常擬合精度的影響,引入地形改正量構(gòu)建高程擬合模型,根據(jù)“移除-恢復(fù)”法,可得高程擬合模型為
ξi=Ha(Xi,Yi,Zi)+ξTC
設(shè)Hi=(Xi,Yi,Zi),則模型表達(dá)式可轉(zhuǎn)化為
ξi=Ha(Hi,ξTC)
考慮地形改正在內(nèi)的最小二乘支持向量機(jī)模型即可由GPS水準(zhǔn)點(diǎn)三維坐標(biāo)和地形改正量作為模型輸入向量,高程異常作為模型輸出向量訓(xùn)練獲得。應(yīng)用到SRTM數(shù)據(jù)正常高獲取中,由大地高與正常高間的關(guān)系表示H大=H正+ξ=H正常+N可知,SRTM正高數(shù)據(jù)疊加EGM96水準(zhǔn)面即可獲得已知點(diǎn)大地高,輸入高程擬合模型即可獲得SRTM數(shù)據(jù)已知點(diǎn)的正常高。
五、試驗(yàn)分析
選取成都黃龍起伏較大的山區(qū)地帶10 km×10 km的區(qū)域范圍, 最大高差為100 m, 布設(shè)20個(gè)GPS水準(zhǔn)點(diǎn)樣本,進(jìn)行四級聯(lián)測,并作歸一化處理。
分別建立樣本點(diǎn)編號,構(gòu)建編號的樣本點(diǎn)如圖2所示。
圖2 樣本編號點(diǎn)圖
選取均勻的6、10、14個(gè)點(diǎn)作為樣本訓(xùn)練集,剩余14、10、6個(gè)點(diǎn)作為測試集,構(gòu)成3種不同的分組方案,分別應(yīng)用于不同的訓(xùn)練模型中。表1為訓(xùn)練集與測試集的3種分組方案。

表1 訓(xùn)練集與測試集分組方案
模型評價(jià)指標(biāo)是用來檢驗(yàn)預(yù)測效果優(yōu)劣的度量,本試驗(yàn)采用均方誤差(MSE)來評價(jià)模型的內(nèi)符合精度和外符合精度,計(jì)算公式為
式中, 內(nèi)符合精度中Δξ為參與擬合計(jì)算的已知點(diǎn)值和擬合值的差值,n為訓(xùn)練點(diǎn)樣本個(gè)數(shù);外符合精度中Δξ為測試點(diǎn)的高程異常擬合值與高程異常實(shí)際值的差值,n為測試點(diǎn)樣本個(gè)數(shù)。本文按照上述3種分組方案應(yīng)用于不同的訓(xùn)練模型中,訓(xùn)練結(jié)果見表2。

表2 不同方案不同模型評價(jià)圖 mm
由表2可知,在已知樣本數(shù)據(jù)較小的情況下,3種訓(xùn)練模型(方案1)精度都比較高,體現(xiàn)了最小二乘支持向量機(jī)在解決小樣本方面的優(yōu)越性。通過對LS-SVM不同算法的改進(jìn)比較得知,無論是內(nèi)符合精度還是外符合精度,無論是整體還是單個(gè)點(diǎn),基于地形改正的CPSO-FLSSVM訓(xùn)練模型都體現(xiàn)了更高的精確度,適用于本課題的研究使用。
六、結(jié) 論
考慮地形在內(nèi)的混沌粒子群優(yōu)化方法、模糊理論及最小二乘向量機(jī)模型,結(jié)合本文算例,可以得出以下結(jié)論:
1) 結(jié)合混沌搜索的隨機(jī)性和遍歷性特點(diǎn),以及粒子群優(yōu)化算法的高效局部搜索能力,將混沌粒子群優(yōu)化方法應(yīng)用于最小二乘向量機(jī)模型的參數(shù)選擇上,避免了人為參數(shù)選擇的不確定性,并且防止了陷入局部最優(yōu)問題。
2) 將模糊思想引入最小二乘向量機(jī)模型,增加模糊隸屬度屬性,來表示樣本對擬合貢獻(xiàn)的程度,解決了LS-SVM對于孤立點(diǎn)過于敏感的問題,使得對影響模型精確度的參數(shù)的調(diào)整更為全面和精確。
3) 考慮到地形起伏對擬合精度的影響,將局部地形改正方法應(yīng)用于地形起伏較大的山區(qū)地帶,提高了山區(qū)地帶的高程擬合精度。
參考文獻(xiàn):
[1] 于小平, 楊國東,王鳳艷,等. GPS高程擬合轉(zhuǎn)換正常高的研究[J].測繪科學(xué),2007,32(2):40-41.
[2] 尹愛明,張楚. 轉(zhuǎn)換GPS 高程的BP 神經(jīng)網(wǎng)絡(luò)方法研究[J].測繪科學(xué),2008,33 (6):78-80.
[3] 孔令杰,李捷斌, 陳偉. 基于遺傳算法的BP神經(jīng)網(wǎng)絡(luò)在高程擬合中的應(yīng)用[J].工程勘察,2010,38(3):61-64.
[4] 黃玉磊,高飛.支持向量機(jī)方法在GPS 高程轉(zhuǎn)換中的應(yīng)用[J].工程勘察,2007(11):64-65.
[5] 謝波,劉連旺.支持向量機(jī)在GPS 高程異常中的應(yīng)用[J]. 測繪科學(xué),2011,36 (1):172-174.
[6] 周理含. 最小二乘支持向量機(jī)在GPS 高程轉(zhuǎn)換中的應(yīng)用[J].工程地球物理學(xué)報(bào),2010,7 (2):243-247.
[7] 湯凱煌.基于地形改正的GPS高程異常曲面的擬合[J].礦山測量,2008(1):35-37.
[8] 黃磊,張書畢,王亮亮,等. 粒子群最小二乘支持向量機(jī)在GPS 高程擬合中的應(yīng)用[J].測繪科學(xué),2010,35 (5):190-192.
[9] 朱樹先,張仁杰.支持向量機(jī)核函數(shù)選擇的研究[J].科學(xué)技術(shù)與工程,2008,8(16):4513-4516.
[10] 禮野.模糊支持向量機(jī)及其在故障診斷中的應(yīng)用[D].沈陽:沈陽航空航天大學(xué),2011.
[11] 張興福,劉成.綜合EGM2008模型SRTM/DTM2006.0剩余地形模型的GPS高程轉(zhuǎn)換方法[J].測繪學(xué)報(bào),2012,41(1):25-32.

