一種改進(jìn)RANSAC的基礎(chǔ)矩陣估計(jì)方法
甄 艷,劉學(xué)軍,王美珍
(1. 南京師范大學(xué) 地理科學(xué)學(xué)院,江蘇 南京 210023;2. 南京師范大學(xué) 虛擬地理環(huán)境教育部重點(diǎn)實(shí)驗(yàn)室,江蘇 南京 210023)
一、引 言
從不同視點(diǎn)處獲得同一場景的兩幅圖像間存在重要的幾何約束關(guān)系,即對極幾何關(guān)系。對極幾何獨(dú)立于場景結(jié)構(gòu),是在非標(biāo)定情況下可以從圖像中獲得的唯一信息。基礎(chǔ)矩陣是對極幾何關(guān)系的代數(shù)表示,它的準(zhǔn)確求解是解決其他視覺問題的關(guān)鍵環(huán)節(jié)之一,如三維重建[1]、運(yùn)動(dòng)估計(jì)、相機(jī)自標(biāo)定[2]、匹配及跟蹤的基礎(chǔ)。目前,利用圖像間對應(yīng)點(diǎn)來估算基礎(chǔ)矩陣的方法主要可以分為3類:線性方法、迭代方法和魯棒方法[3]。線性方法的特點(diǎn)是計(jì)算速度快,但對于噪聲和錯(cuò)誤匹配非常敏感;迭代方法的精度通常比線性方法高,但計(jì)算時(shí)間長。當(dāng)匹配點(diǎn)集中出現(xiàn)錯(cuò)誤匹配時(shí),線性方法和迭代方法已經(jīng)不再適用,而魯棒方法可以解決這類問題,如最小中值法(least median squares,LMedS)、隨機(jī)抽樣一致性法(random sample consensus,RANSAC)及M估計(jì)算法(M-estimator sample consensus,M-Estimators),這類方法的特點(diǎn)是對噪聲和錯(cuò)誤匹配都有更好的魯棒性。當(dāng)錯(cuò)誤數(shù)據(jù)超過50%時(shí),RANSAC仍能獲得較好的結(jié)果,近年來根據(jù)RANSAC算法的思想衍生出MINPRAN算法[4]和MLESAC[5]等算法。
傳統(tǒng)RANSAC算法在外點(diǎn)比率較大時(shí)算法效率較低,Matas和Chum[6]提出的預(yù)檢驗(yàn)算法可有效提高算法效率,陳付幸[7]和田文[8]等在此基礎(chǔ)上重新設(shè)定預(yù)檢驗(yàn)的條件,設(shè)計(jì)了自適應(yīng)的預(yù)檢驗(yàn)方法。RANSAC算法也存在樣本選擇的隨機(jī)性導(dǎo)致結(jié)果具有較大隨機(jī)性的問題,劉坤[9]和魯珊[10]等提出基于概率抽樣的方法來解決這一問題,該方法可在一定程度上提高算法的精度,但由于在模型檢驗(yàn)過程中需要計(jì)算每個(gè)樣本點(diǎn)的抽樣概率并根據(jù)設(shè)定的閾值來選擇樣本點(diǎn),計(jì)算過程較復(fù)雜。針對上述問題,本文提出了一種改進(jìn)RANSAC的基礎(chǔ)矩陣估計(jì)算法。
二、RANSAC算法效率與精度分析
RANSAC算法的基本思想是在保證一定置信概率的前提下,經(jīng)過多次抽樣取得至少一個(gè)樣本包括的點(diǎn)全是無污染的樣本,從而保證得到正確的參數(shù)模型。其計(jì)算過程實(shí)質(zhì)上可看做是模型的假設(shè)與驗(yàn)證的過程,如圖1所示。在模型假設(shè)階段,從原始數(shù)據(jù)中隨機(jī)抽取最小子集來估計(jì)模型參數(shù);在模型驗(yàn)證階段,需要對估計(jì)的模型參數(shù)進(jìn)行驗(yàn)證,驗(yàn)證方法一般是計(jì)算原始數(shù)據(jù)中與估計(jì)的模型參數(shù)相容的樣本數(shù)量。
1. RANSAC算法效率分析
設(shè)原始數(shù)據(jù)中共有N對匹配點(diǎn),從中隨機(jī)抽取一個(gè)最小子集來估計(jì)模型參數(shù)的時(shí)間,記為Cestimate,用一個(gè)數(shù)據(jù)檢驗(yàn)?zāi)P蛥?shù)需要的時(shí)間,記為Cfitting,則用原始數(shù)據(jù)中的全部數(shù)據(jù)檢驗(yàn)?zāi)P蛥?shù)的算法復(fù)雜度為O(NCfitting)。因此,RANSAC算法完成K次樣本假設(shè)與驗(yàn)證的過程算法復(fù)雜度為
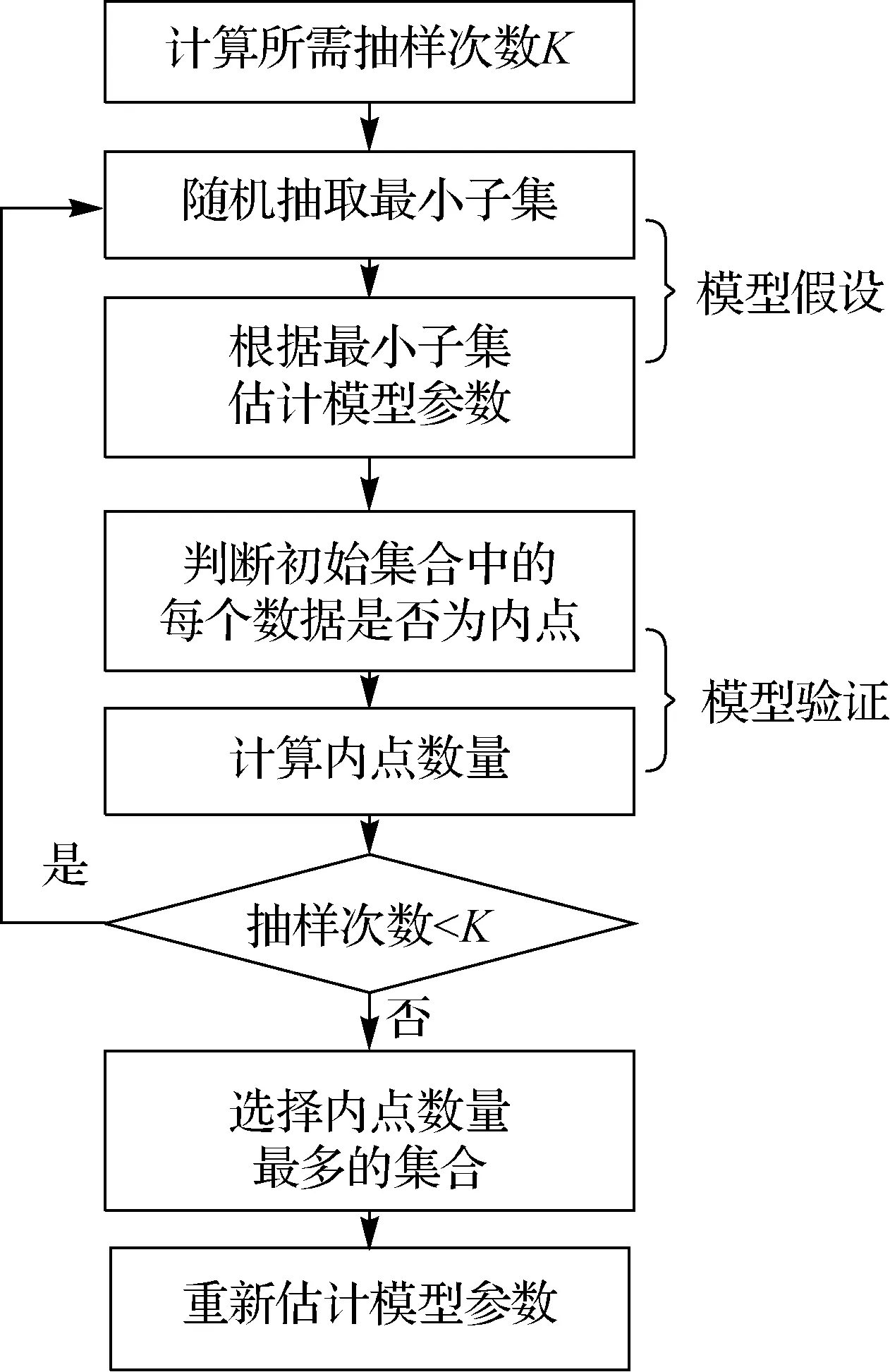
圖1 RANSAC算法流程圖
(1)
從式(1)可以看出,影響RANSAC算法計(jì)算效率的因素主要有兩個(gè):抽樣次數(shù)和模型驗(yàn)證所需時(shí)間。因此,要提高RANSAC算法的效率,可減少抽樣次數(shù)和減少模型驗(yàn)證所需的時(shí)間。
2. RANSAC算法精度分析
由于在特征點(diǎn)提取與匹配過程中不可避免會(huì)含有噪聲和外點(diǎn)數(shù)據(jù),在外點(diǎn)比率較高的情況下,隨機(jī)采樣的數(shù)據(jù)中通常都含有外點(diǎn)數(shù)據(jù),因此,用含有外點(diǎn)的樣本數(shù)據(jù)估計(jì)得到的模型參數(shù)常常含有較大誤差。另外,在模型參數(shù)的檢驗(yàn)過程中,尋找與該模型相容的樣本數(shù)據(jù)時(shí),一般方法是通過設(shè)定的閾值來判斷的。若閾值設(shè)定過大,則會(huì)滲入大量的外點(diǎn)數(shù)據(jù);若閾值設(shè)定過小,則檢驗(yàn)過程會(huì)過分嚴(yán)格,進(jìn)而篩選掉內(nèi)點(diǎn)數(shù)據(jù)。因此,閾值的設(shè)定對算法的精度也有一定的影響。
綜合分析,影響RANSAC算法計(jì)算精度的因素主要有兩個(gè):樣本選擇與閾值設(shè)定,而閾值一般是根據(jù)經(jīng)驗(yàn)值進(jìn)行設(shè)定的,目前沒有更好的解決方案。若原始匹配點(diǎn)集合的質(zhì)量較好,無論采用何種方式選擇樣本數(shù)據(jù)都能得到較好的估計(jì)結(jié)果,而事實(shí)上,到目前為止,沒有一種算法可以完全消除外點(diǎn)的影響。要從根本上提高RANSAC算法的計(jì)算精度,需要較全面地檢測和剔除外點(diǎn)數(shù)據(jù)。
三、改進(jìn)RANSAC的基礎(chǔ)矩陣估計(jì)算法
在基礎(chǔ)矩陣的計(jì)算過程中,估計(jì)模型參數(shù)所需的樣本數(shù)量基本是固定的,一般采用7點(diǎn)法或8點(diǎn)法來估計(jì)初始值。算法在保證一定置信概率的前提下,抽樣次數(shù)與數(shù)據(jù)錯(cuò)誤率有關(guān),一旦數(shù)據(jù)錯(cuò)誤率確定了,算法所需的抽樣次數(shù)也就隨之確定了,很難再改變。因此,通過上述分析,要提高基礎(chǔ)矩陣的計(jì)算效率,可考慮從減少模型參數(shù)的檢驗(yàn)時(shí)間入手,而預(yù)檢驗(yàn)算法在不改變算法精度的前提下,可以很大限度地減小計(jì)算量,提高算法效率。根據(jù)前面對影響RANSAC算法精度的因素分析可知,檢測并剔除外點(diǎn)數(shù)據(jù)是提高算法精度的關(guān)鍵,而一個(gè)好的模型參數(shù)更有利于檢測出外點(diǎn)數(shù)據(jù)。提高RANSAC算法精度的一個(gè)可行方法是在樣本選擇時(shí)盡可能選擇內(nèi)點(diǎn)數(shù)據(jù)來估計(jì)模型參數(shù)。
1. 預(yù)檢驗(yàn)
在RANSAC算法的計(jì)算過程中,大部分抽樣都會(huì)受到外點(diǎn)的影響,對受到外點(diǎn)影響的這部分模型,每次都用全部數(shù)據(jù)去檢驗(yàn),這無疑浪費(fèi)了大量的計(jì)算時(shí)間。預(yù)檢驗(yàn)方法可有效減少模型參數(shù)的檢驗(yàn)時(shí)間,其基本思想是:用少量樣本數(shù)據(jù)來評估模型參數(shù),如果該模型可以通過預(yù)檢驗(yàn),則認(rèn)為當(dāng)前模型是一個(gè)好模型,可接著進(jìn)行后續(xù)的全部數(shù)據(jù)檢驗(yàn);否則認(rèn)為該模型受到外點(diǎn)數(shù)據(jù)的污染,不再參與后續(xù)檢驗(yàn)。加入預(yù)檢驗(yàn)后,雖然不能改善算法精度,其精度與原RANSAC算法基本保持一致,而效率方面卻可大幅提升。
2. 樣本選擇
采用傳統(tǒng)RANSAC算法估計(jì)基礎(chǔ)矩陣時(shí),每次抽樣都是一個(gè)相對獨(dú)立的過程,并沒有考慮前面已完成過程的反饋信息。而實(shí)際上,在前面已完成的抽樣過程中,每次都需要對原始匹配點(diǎn)集中每個(gè)點(diǎn)是否為內(nèi)點(diǎn)進(jìn)行判斷,對于每對匹配點(diǎn)質(zhì)量的好壞,已經(jīng)有了初步的判斷。如果能夠利用前面累積的反饋信息來指導(dǎo)下次抽樣,這無疑將提高抽取樣本的質(zhì)量,從而可以更好地檢測內(nèi)點(diǎn)和外點(diǎn)數(shù)據(jù)。在多次循環(huán)驗(yàn)證的過程中,傳統(tǒng)的RANSAC算法只記錄每個(gè)基礎(chǔ)矩陣初始值對應(yīng)的內(nèi)點(diǎn)總數(shù),而實(shí)際上,在整個(gè)判斷過程中可同時(shí)記錄下每對點(diǎn)是否為內(nèi)點(diǎn)。統(tǒng)計(jì)每對匹配點(diǎn)被標(biāo)記為內(nèi)點(diǎn)的次數(shù),選擇被標(biāo)記為內(nèi)點(diǎn)的次數(shù)較多的這部分點(diǎn)構(gòu)成候選集合。在下一次樣本抽取時(shí),可直接從候選集合中進(jìn)行。由于候選集合中的數(shù)據(jù)是根據(jù)被判斷為內(nèi)點(diǎn)的次數(shù)來確定的,因此,該集合的中的點(diǎn)作為內(nèi)點(diǎn)的概率也大于其他點(diǎn)。每次驗(yàn)證過程結(jié)束后,需要重新計(jì)算每對匹配點(diǎn)被標(biāo)記為內(nèi)點(diǎn)的次數(shù)并更新候選集合,以便指導(dǎo)下一次抽樣。
3. 算法過程
本文算法的基本思想是以傳統(tǒng)RANSAC算法為框架,為提高算法效率與計(jì)算精度,結(jié)合預(yù)檢驗(yàn)方法,選擇被標(biāo)記為內(nèi)點(diǎn)次數(shù)較多的樣本來估計(jì)基礎(chǔ)矩陣初始值。計(jì)算過程可分為初始候選集合構(gòu)成和內(nèi)點(diǎn)集的確定兩個(gè)部分,具體描述如下:
(1) 初始候選集合生成
1) 計(jì)算所需抽樣次數(shù)K。
2) 在前K/3次抽樣中,從原始匹配點(diǎn)集合中隨機(jī)選擇8個(gè)樣本點(diǎn),用改進(jìn)的8點(diǎn)算法計(jì)算基礎(chǔ)矩陣的初始值。
3) 加入預(yù)檢驗(yàn)步驟,在對通過預(yù)檢的初始值進(jìn)行驗(yàn)證的過程中,計(jì)算對應(yīng)的內(nèi)點(diǎn)數(shù)量的同時(shí)標(biāo)記每對匹配點(diǎn)是否為內(nèi)點(diǎn)。
4) 完成K/3次抽樣后,計(jì)算到目前為止每對匹配點(diǎn)被標(biāo)記為內(nèi)點(diǎn)的次數(shù),選擇被標(biāo)記內(nèi)點(diǎn)次數(shù)較多的匹配點(diǎn)對構(gòu)成初始候選集合。
(2) 內(nèi)點(diǎn)集確定
1) 在余下的抽樣過程中,采用前面介紹的樣本選擇方法,從候選集合中選擇最小子集來估計(jì)基礎(chǔ)陣的初始值。
2) 結(jié)合預(yù)檢驗(yàn)方法,若當(dāng)前模型參數(shù)通過預(yù)檢驗(yàn),計(jì)算其對應(yīng)的內(nèi)點(diǎn)數(shù)量并重新計(jì)算初始集合中每對匹配點(diǎn)被標(biāo)記為內(nèi)點(diǎn)的次數(shù)。
3) 更新候選集合。
4) 完成K次抽樣后,選擇包含內(nèi)點(diǎn)數(shù)量最多的集合作為內(nèi)點(diǎn)集。
5) 根據(jù)確定的內(nèi)點(diǎn)集,采用M-Estimators方法重新估計(jì)基礎(chǔ)矩陣,并將結(jié)果作為最優(yōu)值返回。
四、試驗(yàn)結(jié)果與分析
為了驗(yàn)證本文算法的有效性和魯棒性,分別對大量的模擬數(shù)據(jù)和真實(shí)圖像數(shù)據(jù)進(jìn)行了試驗(yàn),將本文算法與M-Estimators、LMedS和RANSAC 3種經(jīng)典魯棒方法進(jìn)行對比,用點(diǎn)到對應(yīng)極線的平均對極距離來精確反映基礎(chǔ)矩陣的估計(jì)精度,對極距離越小,說明基礎(chǔ)矩陣的估計(jì)精度越高。由于篇幅所限,本文直接給出部分試驗(yàn)結(jié)果。
1. 模擬數(shù)據(jù)和真實(shí)圖像試驗(yàn)
模擬數(shù)據(jù)是采用程序生成同一場景不同視角兩幅圖像的匹配點(diǎn)對,數(shù)量為100。添加均值為0,方差為1.0的高斯噪聲后,不同外點(diǎn)比率下4種算法的計(jì)算精度比較結(jié)果如圖2所示。表1為在外點(diǎn)比率為20%的情況下,不同噪聲下4種算法的計(jì)算精度比較。
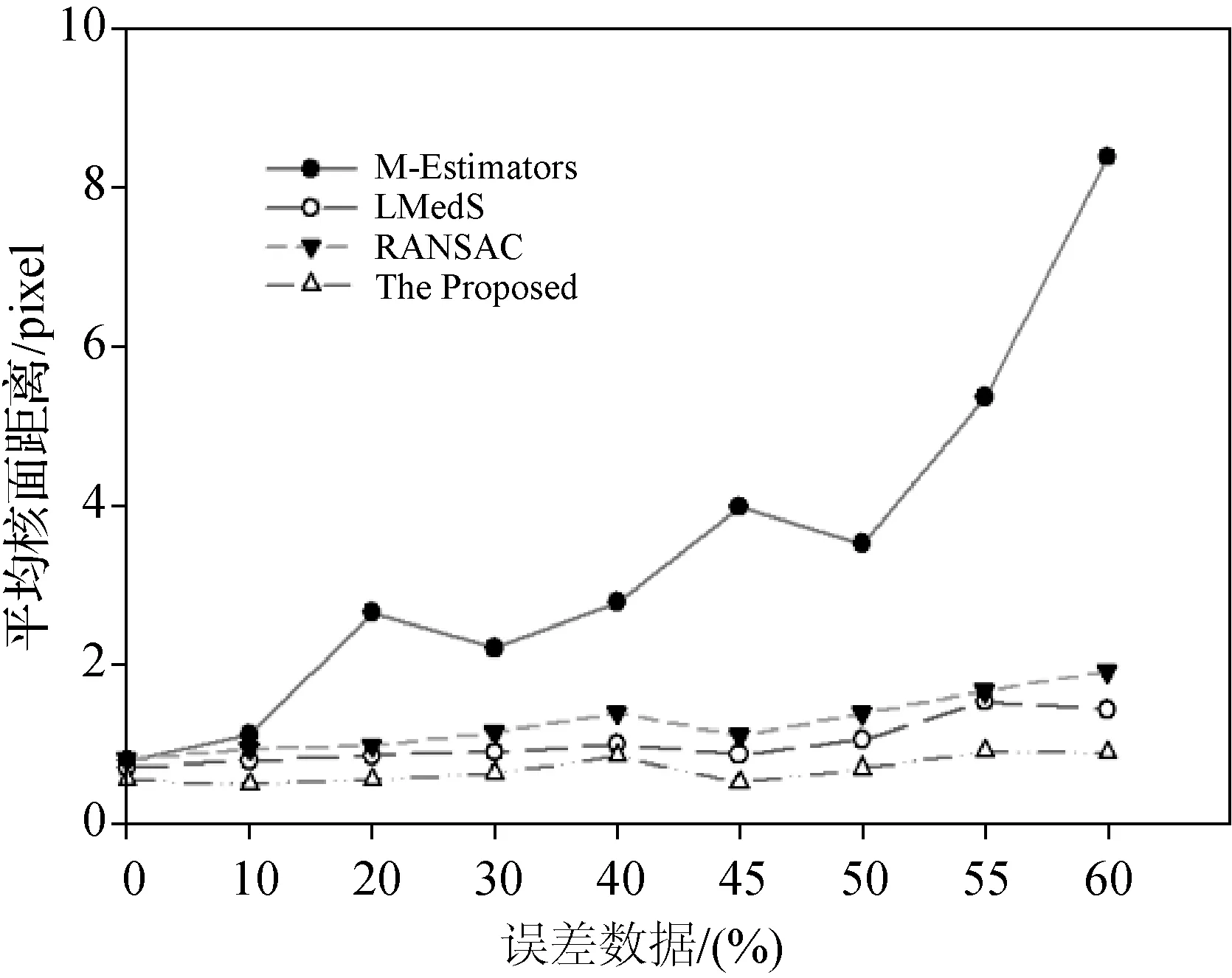
圖2 4種方法在不同比率外點(diǎn)數(shù)據(jù)情況下的平均對極距離
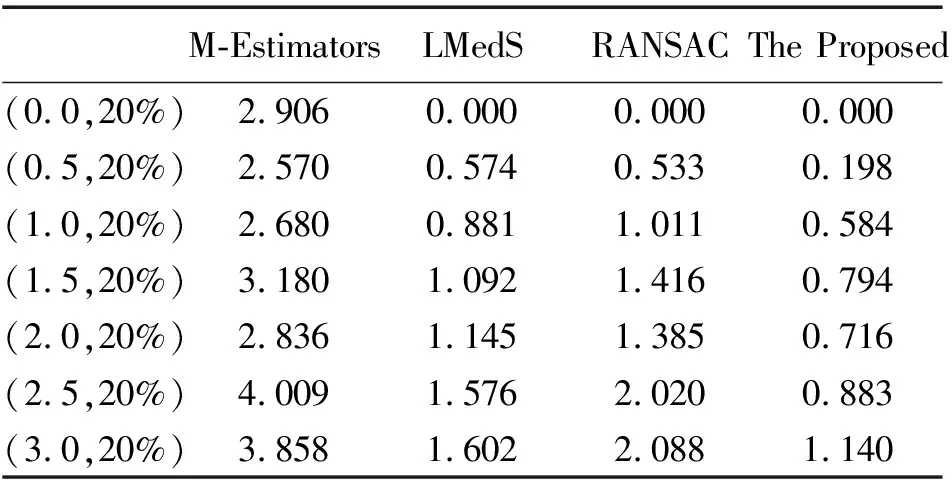
表1 不同噪聲情況下的平均對極距離 像素
圖3為采用SIFT算法對兩幅圖像進(jìn)行特征提取與匹配獲得初始匹配集合的效果圖。其中,場景1包含的匹配點(diǎn)數(shù)量相對較多,共1247對;場景2包含147對,相對少一些。之所以選擇這兩幅圖像,是由于其包含的匹配點(diǎn)數(shù)量有較大差別,可驗(yàn)證在不同匹配點(diǎn)數(shù)量下算法的魯棒性。表2給出了每個(gè)場景通過上述4種算法獲得的平均對極距離和標(biāo)準(zhǔn)偏差。

圖3 兩幅圖像特征提取與匹配效果圖
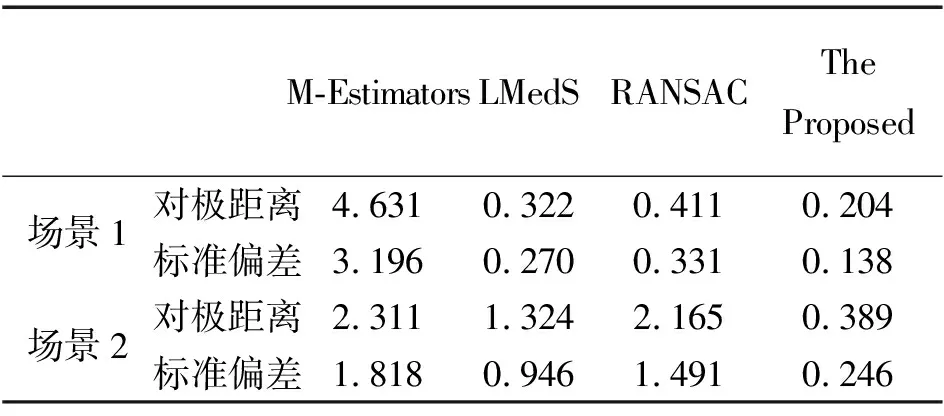
表2 4種方法對真實(shí)圖像數(shù)據(jù)的計(jì)算結(jié)果 像素
2. 計(jì)算精度分析
從上述試驗(yàn)結(jié)果來看,無論模擬數(shù)據(jù)還是真實(shí)圖像試驗(yàn)數(shù)據(jù),本文算法的結(jié)果均優(yōu)于其他3種方法。在不同比率的外點(diǎn)數(shù)據(jù)下,M-Estimators方法隨著外點(diǎn)比率的增大誤差最大,LMedS方法的精度略優(yōu)于RANSAC方法,本文算法一直能保持較高精度。從表1的試驗(yàn)結(jié)果可以看出,隨著噪聲的增大,4種算法的精度都有所降低,M-Estimators方法受噪聲影響最大。當(dāng)噪聲強(qiáng)度超過1.0時(shí),LMedS方法和RANSAC方法的誤差較大,而本文方法在噪聲強(qiáng)度為3.0時(shí),仍能保持較高的精度。從真實(shí)圖像試驗(yàn)結(jié)果來看,無論匹配點(diǎn)數(shù)量的多少,本文算法的結(jié)果都優(yōu)于其他3種方法。當(dāng)匹配點(diǎn)數(shù)量較少,且外點(diǎn)率較高時(shí),算法體現(xiàn)出更好的性能。
綜合分析,本文算法的計(jì)算精度優(yōu)于其他3種方法,這主要得益于兩個(gè)方面:一方面是本文算法在樣本選擇時(shí)從被判斷為內(nèi)點(diǎn)次數(shù)較多的點(diǎn)中抽取樣本點(diǎn)來估計(jì)模型參數(shù),選擇的樣本點(diǎn)作為內(nèi)點(diǎn)的概率較大,為下一步處理提供了較好的模型參數(shù),可以更準(zhǔn)確地判斷內(nèi)外點(diǎn);另一方面是在獲得內(nèi)點(diǎn)集的基礎(chǔ)上,采用M-Estimators方法迭代處理不斷優(yōu)化,進(jìn)一步去除對結(jié)果影響較大的匹配點(diǎn),從而提高了算法的估計(jì)精度。
3. 計(jì)算效率分析
為考察本文算法的計(jì)算效率,分別計(jì)算不同外點(diǎn)比率和不同匹配點(diǎn)數(shù)量下4種算法的計(jì)算時(shí)間。不同外點(diǎn)比率下算法的計(jì)算時(shí)間如圖4所示,試驗(yàn)數(shù)據(jù)中添加有均值為0,方差為1.0的高斯噪聲。不同匹配點(diǎn)數(shù)量下算法的計(jì)算時(shí)間以場景1為例,圖5為試驗(yàn)結(jié)果。
從圖4可以看出,在外點(diǎn)比率小于40%時(shí),4種算法的計(jì)算時(shí)間差別不大,隨著外點(diǎn)比率的增大,M-Estimators算法一直保持較高的計(jì)算效率,而RANSAC算法的計(jì)算時(shí)間呈指數(shù)增長;當(dāng)外點(diǎn)比率超過50%時(shí),除M-Estimators算法外,其他3種方法的計(jì)算時(shí)間會(huì)隨著外點(diǎn)比率的增加而增大;當(dāng)外點(diǎn)比率增加到60%時(shí),本文算法所需計(jì)算時(shí)間遠(yuǎn)小于RANSAC方法與LMedS方法。從圖5可以看出,隨著匹配點(diǎn)數(shù)量的增多,4種算法的計(jì)算時(shí)間也隨之增長,LMedS方法的計(jì)算時(shí)間增加最快,M-Estimators的計(jì)算時(shí)間雖然也有所增加,但其計(jì)算效率仍是4種方法中最高的。而本文算法的計(jì)算效率仍優(yōu)于LMedS方法與RANSAC方法。

圖4 不同外點(diǎn)比率下4種算法的計(jì)算時(shí)間

圖5 不同匹配點(diǎn)數(shù)量下4種算法的計(jì)算時(shí)間
4. 本文算法與PARANSAC算法比較
魯珊[10]等針對隨機(jī)抽樣一致性算法效率低的問題,提出了一種基于概率分析的隨機(jī)抽樣一致性算法(PARANSAC)。為進(jìn)一步驗(yàn)證本文算法的精度與效率,將本文算法與PARANSAC算法對比,試驗(yàn)數(shù)據(jù)采用文獻(xiàn)[10]中的真實(shí)圖像數(shù)據(jù),結(jié)果如圖6所示。從表3的試驗(yàn)結(jié)果來看,本文算法在計(jì)算精度與效率上均優(yōu)于PARANSAC算法。本文算法樣本選擇策略簡單,不增加額外的計(jì)算開銷,而PARANSAC算法在每次迭代過程中都需要計(jì)算每對匹配點(diǎn)的概率,并且在計(jì)算過程中需要設(shè)置合適的閾值,閾值設(shè)置不當(dāng)將嚴(yán)重影響計(jì)算結(jié)果。

圖6 不同角度的2組真實(shí)圖像
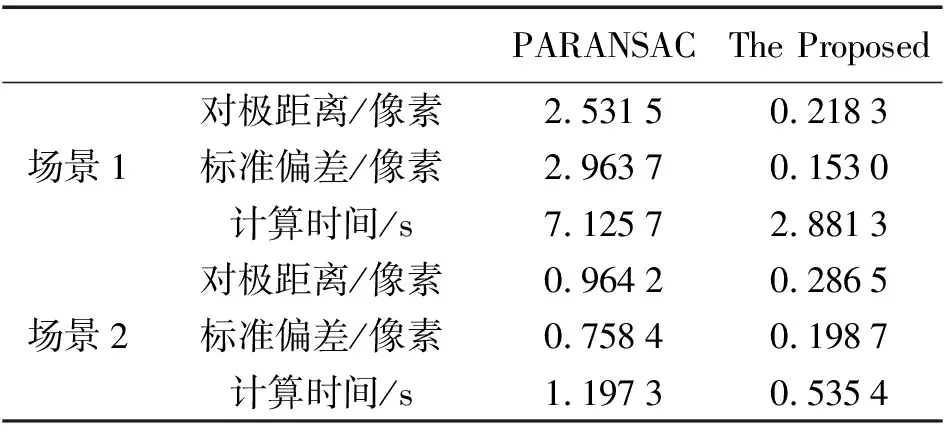
表3 計(jì)算精度與效率比較
五、結(jié)束語
本文針對采用傳統(tǒng)RANSAC算法進(jìn)行基礎(chǔ)矩陣計(jì)算時(shí)效率較低和樣本選擇隨機(jī)性的問題,提出了一種改進(jìn)RANSAC的基礎(chǔ)矩陣計(jì)算方法。該算法通過加入預(yù)檢驗(yàn)步驟去除明顯錯(cuò)誤的模型,減少了大量的無用計(jì)算,提高了算法效率。由于被標(biāo)記為內(nèi)點(diǎn)次數(shù)較多的點(diǎn)作為內(nèi)點(diǎn)的概率要大于其他數(shù)據(jù),因此,根據(jù)被標(biāo)記為內(nèi)點(diǎn)次數(shù)的多少為標(biāo)準(zhǔn)來指導(dǎo)后續(xù)抽樣,提高了獲得好的模型參數(shù)的概率,從而可以更好地檢測并剔除外點(diǎn)數(shù)據(jù)。最后在確定內(nèi)點(diǎn)的基礎(chǔ)上,采用M-Estimators方法進(jìn)一步提高解算精度。試驗(yàn)結(jié)果表明,本文算法不僅可以有效剔除錯(cuò)誤匹配點(diǎn),提高基礎(chǔ)矩陣的計(jì)算精度,并且在魯棒性和計(jì)算效率方面也較優(yōu)。
參考文獻(xiàn):
[1] 宋宏權(quán),劉學(xué)軍,閭國年,等. 地理參考下未標(biāo)定圖像序列的三維點(diǎn)云精度分析[J]. 測繪通報(bào),2012(7):14-16,20.
[2] 季錚,張劍清,詹總謙. 基于序列影像和積分法的復(fù)雜物體三維重建[J]. 測繪通報(bào),2008(1):26-29.
[3] ARMANGUE X, SALVI J. Overall View Regarding Fundamental Matrix Estimation[J]. Image and Vision Computing,2003,21(2): 205-220.
[4] STEWART C V. MINPRAN: A New Robust Operator for Computer Vision:Application to Range Data[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1995, 17(10): 925-938.
[5] TORR P H S, ZISSERMAN A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry[J]. Computer Vision and Image Understanding, 2000, 78(1): 138-156.
[6] MATAS J, CHUM O. Randomized RANSAC withTd,dTest[J]. Image and Vision Computing, 2004, 22(10): 837-842.
[7] 陳付幸,王潤生. 基于預(yù)檢驗(yàn)的快速隨機(jī)抽樣一致性算法[J]. 軟件學(xué)報(bào),2005,16(8): 1431-1437.
[8] 田文,王宏遠(yuǎn),徐帆,等. RANSAC算法的自適應(yīng)Tc,d 預(yù)檢驗(yàn)[J]. 中國圖象圖形學(xué)報(bào),2009,14(5): 973-977.
[9] 劉坤,葛俊鋒,羅予頻,等. 概率引導(dǎo)的隨機(jī)采樣一致性算法[J]. 計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào),2009,21(5):657-662.
[10] 魯珊,雷英杰,孔韋韋,等. 基于概率抽樣一致性算法的基礎(chǔ)矩陣估計(jì)算法[J]. 控制與決策,2012,27(3): 425-430.

