語義支持下的土地利用柵格數據制圖綜合研究

孔凡強，楊 俊,2，王詩陽

(1. 自然地理與空間信息科學遼寧省重點實驗室，遼寧 大連 116029；2. 中國科學院地理科學與資源研究所，北京100101)

一、引 言

制圖綜合是地圖制圖學的關鍵問題，隨著計算機與GIS技術的發展，自動綜合的研究也隨之深入，許多學者投身于此，其研究重點主要集中在矢量數據，主要研究內容有：點抽稀、邊界化簡、圖斑剖分降維處理等[1-5]。實際上，在綜合的某些方面柵格數據較矢量數據更有優勢：柵格數據高度結構化，是由一系列的像元點組成的平面數據，在進行鄰域分析時更簡單快速，而矢量數據很難提取出完整的鄰域圖斑進行分析；易于構建數學模型及進行疊加運算。因此柵格數據綜合模型的構建較矢量數據更加容易。在此之前已有學者研究了柵格數據在制圖綜合中的應用：20世紀80年代，Monmonier就已經將數學形態學應用于柵格模型面狀要素地圖綜合，隨后又有其他學者對數學形態學在地圖綜合中的應用作了進一步研究[6-9]。但是僅僅利用數學形態學來處理柵格數據很難實現完整的制圖綜合過程，這就需要元胞自動機的協助。在前人的研究和努力下，目前有眾數濾波運算規則的元胞自動機適應于制圖綜合，并應用于某些專題圖的綜合中[10- 11]。

根據土地利用柵格數據的特點，本文以數學形態學中的閉運算來實現圖斑的聚合。在眾數濾波運算規則的元胞自動機運算中添加語義概念實現綜合，更能表達土地利用數據的語義關聯性，進一步縮小綜合前后各地類面積變化量。下面介紹基本的理論依據及實現步驟，并給出程序詳細的流程設計。

二、理論依據與算法過程

1. 數學形態學

數學形態學以集合算子為基礎，其最基本的運算就是腐蝕與膨脹運算，其中腐蝕運算類似于矢量面狀數據建立內緩沖區，膨脹類似于建立外緩沖區，但是腐蝕與膨脹的形狀由結構元控制。在腐蝕與膨脹運算的基礎上演化出了開、閉運算，而在制圖綜合中聚合運算是由閉運算實現的。

膨脹運算：A⊕B={a+b:∈A,∈B}

(1)

腐蝕運算：AΘB={a:a+b∈A,∈B}

(2)

式中，A為待處理的像素點集合；B也是一個集合，稱為結構元。公式(1)表示集合A被結構元B膨脹，公式(2)表示集合A被結構元B腐蝕。

數學形態學中膨脹與腐蝕運算的詳細過程如圖1所示，集合中是0與1的二值圖，灰色表示1，白色為0。圖1(a)表示集合A，圖1(b)表示結構元B，這里的結構元采用焦點四鄰域像元。膨脹運算的基本過程是將結構元B沿著集合A的行列依次滑行。若結構元中心位置對應于集合A的像元值為1，則其四個鄰域也變為1，否則為0。集合A經過結構元B的1次膨脹運算后得到的結果如圖1(c)所示，被膨脹的像元在圖中用“+”表示。腐蝕運算的過程正好與膨脹運算相反，當結構元中心位置對應于集合A的像元值為0時，其四個鄰域也變為0。集合A經過結構元B的1次腐蝕運算后得到的結果如圖1(d)所示，被腐蝕的像元在圖中用“-”表示。較為復雜的閉運算就是先經過膨脹再經過相應次數的腐蝕運算達到連接臨近斑塊的效果；開運算的運算步驟正好相反。

由數學形態學閉運算的特點，對柵格化后的距離臨近卻相離的圖斑，先經過若干次的膨脹運算，再進行相應次數的腐蝕運算，即可實現制圖綜合中的聚合效果。開運算基本式如式(3)，但是在實際運用中腐蝕與膨脹的次數可能要根據聚合地類的距離而定。

開運算：A·B= ((A⊕B)ΘB)

(3)

數學形態學處理聚合的過程如圖2所示，圖2(a)為待聚合的兩個圖斑，圖2(b)為聚合采用的結構元，圖2(c)為膨脹腐蝕運算各一次后得到的結果。而在實際中如果兩個圖斑塊距離為n，則需先進行n/(2*cellsize)次膨脹運算，再進行相應次數的腐蝕運算，即可實現聚合運算。

2. 元胞自動機

僅通過數學形態學是很難實現土地利用柵格數據綜合的，因為土地利用數據是多語義的復雜數據集合，而數學形態學僅能處理二值圖，在對多個地類綜合分析處理時就顯得能力不足了。因此還需要元胞自動機的輔助處理，即對數學形態學聚合處理完后的數據進行基于眾數濾波規則的元胞自動機處理，實現要素邊線簡化和小圖斑的融合。

元胞自動機由元胞、元胞空間、鄰居及規則四部分組成。元胞就是像元點；元胞空間就是元胞所分布的空間；鄰居的定義較復雜，在二維空間中，鄰居主要有3種：馮-諾依曼型、摩爾型和擴展摩爾型；規則根據研究對象和研究領域的不同復雜多變，但其本質是一個狀態轉移函數。在土地利用柵格數據綜合中，規則的制定決定著綜合質量的優劣，本文根據土地利用數據的特點，提出基于空間和語義綜合比較競爭的柵格變換規則。

如圖3所示，若像元a為待計算的焦點，采用8鄰域的鄰居進行規則轉換，1～8是a的8鄰域。設該時刻為t，則t+1時刻a像元點的屬性規則如下：如果a周圍沒有與其屬同一大類的像元點，或a周圍的像元點全部與其屬同一大類，則t+1時刻a轉換為其鄰域所占柵格個數最多的像元點的取值；否則，取出a鄰居中與其屬同一大類且柵格個數最多的地類，標記其個數i，同時取出與其不屬于同一大類且柵格個數最多的地類，標記其個數j，并判斷i×m與j×n的大小(m，n分別為i對應地類與j對應地類對a的競爭力，即m個i對應的地類與n個j對應的地類競爭力相同)，取大值作為a像元點t+1時刻的取值。圖3中，若a與5屬同一大類，與8不屬同一大類，雖然t時刻a的鄰居中兩地類都有3個像元，但是t+1時刻a的值為5處的地類；若a與3屬同一大類，與2不屬同一大類，但num(landtype(3))×2< num(landtype(2))×1(這里暫設m與n分別為2，1)，則t+1時刻a需要轉換為2處的地類。

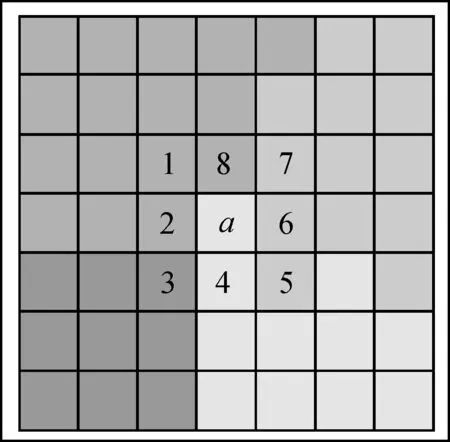
圖3 元胞自動機規則說明圖

元胞自動機是離散的空間集合在有限的狀態中按一定的規則隨離散的時間變化，將其應用于土地利用柵格數據的綜合，并不能一蹴而就，而是漸進式的，需要經過多次迭代才能達到較為理想的效果。

3. 算法流程圖

本文采用GDAL開源柵格空間數據轉換庫存取數據，利用numpy科學計算包中的數組對象Array進行柵格矩陣運算，實現數學形態學中的閉運算及建立元胞自動機的模型，運算簡便高效。模型流程如圖4所示。

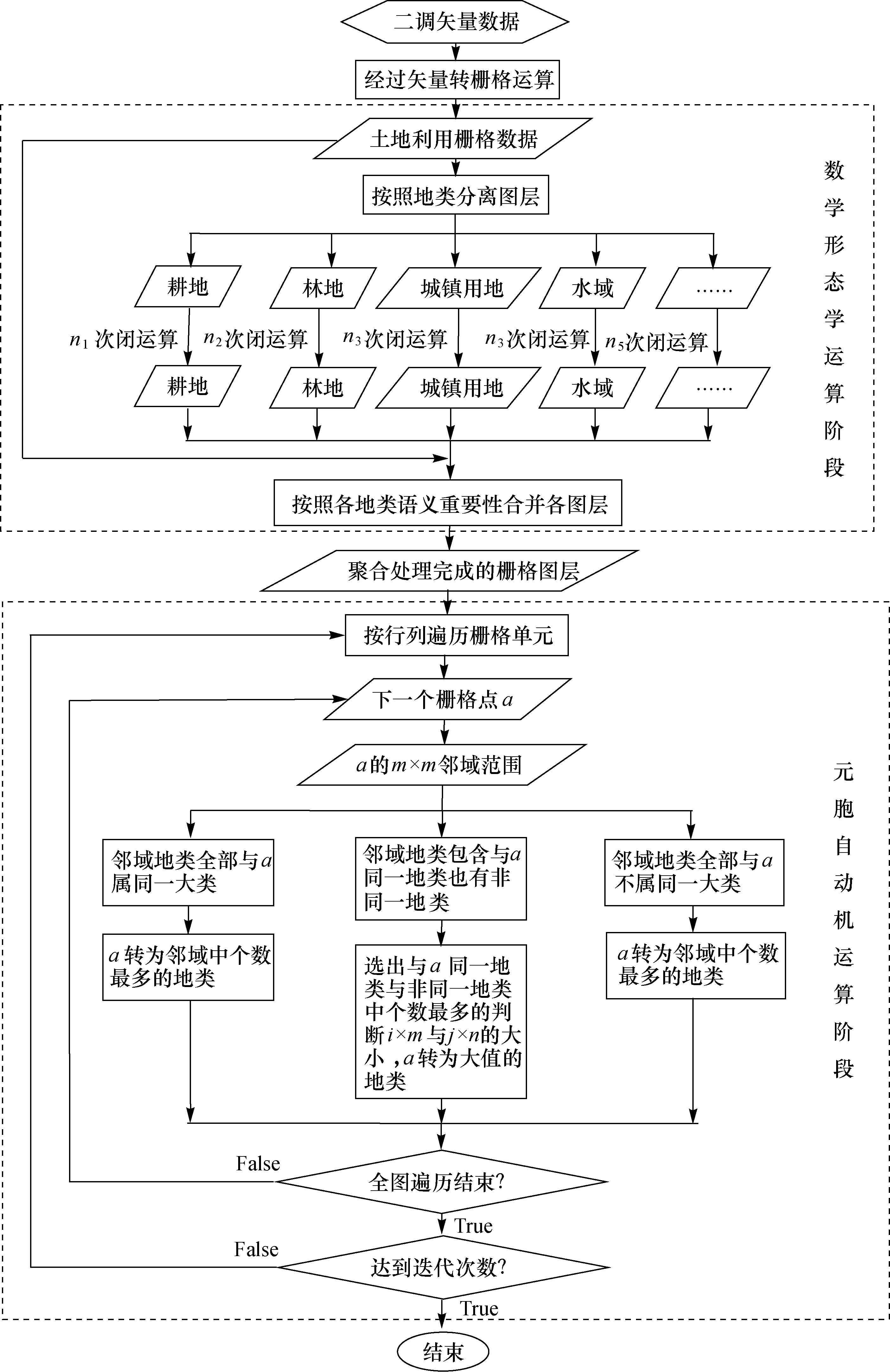
圖4 模型流程圖

三、結果與討論

本文在前人的研究基礎上，建立了語義支持下土地利用柵格數據綜合模型，相比之下更符合土地利用數據的特點。以旅順口區北海街道二調數據為試驗對象進行研究，將矢量數據以5 m分辨率轉為柵格，元胞自動機鄰域采用3×3的8鄰域，數據結果如圖5所示。圖5(a)為二調矢量數據轉柵格后的數據，圖5(b)為數學形態學運算后再經本文元胞自動機模型迭代處理20次后的數據，圖5(c)為經元胞自動機模型迭代處理40次后的數據。由圖5可以分析得出：數學形態學能很好地解決圖斑聚合運算；CA運算能夠實現圖斑邊界的平滑，由于本文加入語義判斷，使得屬同一大類的相鄰斑塊運算后邊界更加平滑，但對于不屬同一大類的斑塊邊界之間變動較小，這取決于前文競爭力的設置；另外，隨著元胞自動機迭代次數的增加，土地利用數據趨于穩定。但是，本文元胞運算規則在處理小圖斑融合問題上還有待提高。總之，柵格數據邊線平滑處理較矢量數據容易，但柵格數據綜合中較難把握比例尺變化，這將是筆者進一步研究的重點。

圖5 處理結果圖

參考文獻：

[1] 艾廷華，郭仁忠，陳曉東. Delaunay三角網支持下的多邊形化簡與合并[J]. 中國圖象圖形學報，2001，6(7): 93-99.

[2] 錢海忠，武芳，陳波，等. 采用斜拉式彎曲劃分的曲線化簡方法[J]. 測繪學報，2007，36(4): 443-449.

[3] 黃萬里，戴文遠，余珊. 基于面積保持的Douglas-Peucker改進算法的多邊形化簡[J]. 科學技術與工程，2009，9(24): 7325-7328.

[4] 艾廷華，劉耀林. 土地利用數據綜合中的聚合與融合[J]. 武漢大學學報：信息科學版， 2002，27(5): 486-492.

[5] 李建林，朱德海，宋曉眉，等. 一種基于面積平衡約束的圖斑化簡算法[J]. 地理與地理信息科學，2009，25(1): 103-106.

[6] MONMONIER M S. Raster-mode Area Generalization for Land Use and Land Cover Maps[J]. Cartographica: The International Journal for Geographic Information and Geovisualization，1983, 20(4): 65-91.

[7] LI Z, SU B O. Algebraic Models for Feature Displacement in the Generalization of Digital Map Data Using Morphological Techniques[J]. Cartographica: The International Journal for Geographic Information and Geovisualization，1995, 32(3): 39-56.

[8] SU B, LI Z. An Algebraic Basis for Digital Generalization of Area-patches Based on Morphological Techniques[J]. The Cartographic Journal, 1995,32(2): 148-153.

[9] SU B, LI Z, LODWICK G. Morphological Transformation for the Elimination of Area Features in Digital Map Generalization[J]. Cartography，1997, 26(2): 23-30.

[10] 章莉萍. 基于柵格模式的地圖圖形自動綜合研究[D]. 武漢：武漢大學, 2009.

[11] 張蘇. 數學形態學與元胞自動機相結合的土地利用制圖綜合方法研究[D]. 西安：西北大學, 2011.