改進(jìn)的三角高程法在跨海高程傳遞中的應(yīng)用

徐亞明，施 斌，王代雄，潘正風(fēng)

(1. 武漢大學(xué) 測(cè)繪學(xué)院，湖北 武漢 430079； 2. 精密工程與工業(yè)測(cè)量國(guó)家測(cè)繪地理信息局重點(diǎn)實(shí)驗(yàn)室，湖北 武漢 430079)

一、引 言

跨海高程傳遞是建立國(guó)家統(tǒng)一的陸海高程基準(zhǔn)框架網(wǎng)的一種重要手段。目前，跨海高程傳遞的方法通常有三角高程測(cè)量法、短期驗(yàn)潮法、GPS水準(zhǔn)法和重力測(cè)量法。短期驗(yàn)潮法是根據(jù)一定海域內(nèi)陸海潮汐一致的特點(diǎn)，通過(guò)觀測(cè)陸海各自距水尺零點(diǎn)的潮位高并求取高差，實(shí)現(xiàn)陸海高程的傳遞，其觀測(cè)精度與時(shí)間成正相關(guān)。GPS水準(zhǔn)法利用靜態(tài)測(cè)量獲得的高精度大地高差與似大地水準(zhǔn)面差距之差來(lái)傳遞高程[1]。該方法相對(duì)實(shí)施周期短且方便實(shí)用，但前提是需要高精度的局部似大地水準(zhǔn)面模型。李建成等已成功利用GPS觀測(cè)所得的相對(duì)大地高差，聯(lián)合精確的似大地水準(zhǔn)面模型，將黃海高程傳遞到了距離上海30 km的洋山島上，其精度與獨(dú)立的潮位觀測(cè)差值為厘米級(jí)，與三等水準(zhǔn)測(cè)量相差為毫米級(jí)[1]。重力測(cè)量法應(yīng)用重力位與高程的關(guān)系，計(jì)算陸地高程起算點(diǎn)的重力位值，根據(jù)跨海重力位差計(jì)算公式和海洋重力場(chǎng)資料計(jì)算出海域某點(diǎn)重力位值，確定該點(diǎn)相對(duì)陸地高程基準(zhǔn)的高程值，實(shí)現(xiàn)跨海高程基準(zhǔn)的精確傳遞。該方法可以快捷準(zhǔn)確地將海域GPS大地高轉(zhuǎn)化為1985國(guó)家高程系統(tǒng)的高程值，精度優(yōu)于10 cm[2]。

三角高程測(cè)量是跨海高程傳遞中一種應(yīng)用比較廣泛的技術(shù)。其基本思想是根據(jù)由已知高程點(diǎn)向目標(biāo)點(diǎn)觀測(cè)所得的豎角和水平距離，計(jì)算兩點(diǎn)間的高差，從而進(jìn)行高程的傳遞[3]。歐陽(yáng)桂崇等在一段10 km長(zhǎng)的跨海段高程傳遞中，利用三角高程測(cè)量獲得的結(jié)果與水準(zhǔn)測(cè)量、重力測(cè)量、GPS水準(zhǔn)及天文重力水準(zhǔn)測(cè)量的符合精度均小于5 mm/km，達(dá)到二等水準(zhǔn)要求。三角高程測(cè)量的精度主要受大氣折光影響，在跨海高程傳遞中，《國(guó)家一、二等水準(zhǔn)測(cè)量規(guī)范》(GB/T 12897—2006)規(guī)定采用大地四邊形結(jié)構(gòu)，利用同步對(duì)向觀測(cè)方式來(lái)消除大氣折光誤差[3]。本文在此規(guī)范的基礎(chǔ)上，提出一種線形結(jié)構(gòu)的觀測(cè)方式結(jié)合相對(duì)嚴(yán)格的同步對(duì)向觀測(cè)，降低了原方式的復(fù)雜程度和觀測(cè)量，取得了較好的效果。

二、精密三角高程測(cè)量原理

精密三角高程測(cè)量在三角高程測(cè)量基本原理的基礎(chǔ)上，采用兩臺(tái)帶有自動(dòng)照準(zhǔn)(ATR)功能的高精度全站儀，經(jīng)改裝后，照準(zhǔn)棱鏡固定在全站儀的把手上，同時(shí)進(jìn)行對(duì)向觀測(cè)，其高差計(jì)算公式如下[4]

hAB=0.5×[(SABtanαAB-SABtanαBA)-

(1)

hAB=0.5×(SABtanαAB-SABtanαBA)

(2)

另外，在起始站和結(jié)束站上觀測(cè)的高差計(jì)算公式為

hAB=SABtanαAB

(3)

三、測(cè)量方案

1. 點(diǎn)位布設(shè)

觀測(cè)點(diǎn)位布設(shè)如圖1所示。在測(cè)線S1—S2之間選擇1、2、3三個(gè)臨時(shí)點(diǎn)作為全站儀設(shè)站點(diǎn)。1點(diǎn)離S1點(diǎn)的距離及3點(diǎn)離S2點(diǎn)的距離限制為5～20 m，1、2點(diǎn)之間為跨海對(duì)向觀測(cè)邊，為了使對(duì)向觀測(cè)邊數(shù)是偶數(shù)，需設(shè)置2、3點(diǎn)之間為過(guò)渡對(duì)向觀測(cè)邊。另外，為了保證觀測(cè)質(zhì)量，要求1、2點(diǎn)之間通視良好，設(shè)置在較高處，使視線高出水面(一般在10 m以上)。

圖1 觀測(cè)點(diǎn)布設(shè)圖

2. 儀器選用及改裝

根據(jù)式(2)、式(3)可知，測(cè)量的精度取決于對(duì)向觀測(cè)的平距值SAB及豎角觀測(cè)值αAB、αBA的觀測(cè)精度，由于跨海高程傳遞中豎角都非常小，SAB的測(cè)量精度很容易控制在1 cm以內(nèi)，這樣SAB的精度對(duì)最終高差的影響很小，可以不予考慮。因此，跨海高程傳遞測(cè)量的精度主要取決于測(cè)量?jī)x器的豎角觀測(cè)精度。本次選用的Leica TM30高精度智能全站儀測(cè)角精度為±0.5″，測(cè)距精度為±(1 mm+1×10-6D)，在ATR模式下測(cè)量范圍為3000 m。精密三角高程測(cè)量需要對(duì)儀器進(jìn)行必要的改裝。改裝后的儀器如圖2所示，在TM30的把手位置安裝圓棱鏡，用于進(jìn)行跨海段的對(duì)向觀測(cè)。

3. 與傳統(tǒng)方法比較

若按照傳統(tǒng)的測(cè)距三角高程測(cè)量方式，根據(jù)規(guī)范要求需要布設(shè)成大地四邊形，如圖3(a)所示，兩岸共需埋設(shè)4個(gè)固定點(diǎn)[4]，觀測(cè)程序較為復(fù)雜。同時(shí)，跨海段觀測(cè)視線為大地四邊形的兩條對(duì)邊，各觀測(cè)邊將受到不同大氣折光的影響，難以直接消除。

而采用改進(jìn)后的線性結(jié)構(gòu)布設(shè)方式(如圖3(b)所示)，只需布設(shè)兩個(gè)固定點(diǎn)，觀測(cè)程序?qū)⒃诤艽蟪潭壬系玫胶?jiǎn)化，且觀測(cè)視線可近似認(rèn)為是對(duì)向觀測(cè)，根據(jù)式(1)、式(2)相關(guān)理論，可以快速地消除大氣折光的影響。

圖2 改裝后的TM30全站儀

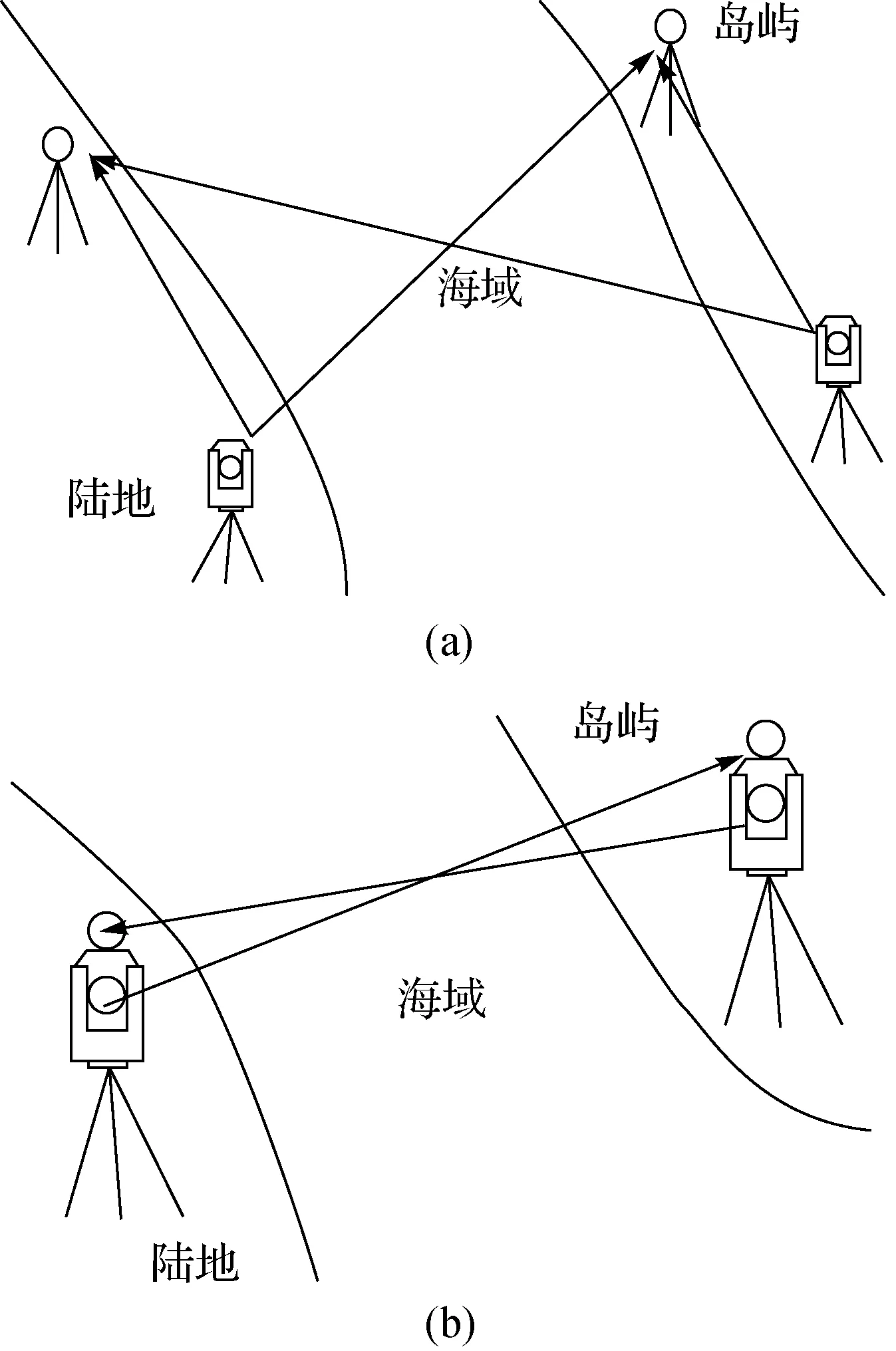
圖3 觀測(cè)示意圖

4. 觀測(cè)方案

本次測(cè)量利用TM30的ATR功能，無(wú)人工照準(zhǔn)測(cè)量。為保證觀測(cè)質(zhì)量，根據(jù)不同的氣象條件，制訂不同的對(duì)向觀測(cè)方法，見(jiàn)表1。

表1 不同氣象條件下的觀測(cè)方案

續(xù)表1

此外，為減小測(cè)角中誤差，一般采用多測(cè)回的方法。實(shí)際觀測(cè)中每組觀測(cè)4測(cè)回，保證每組的測(cè)角中誤差都在0.5″之內(nèi)。

(1) 起點(diǎn)觀測(cè)

在1點(diǎn)架設(shè)全站儀，在S1點(diǎn)上架設(shè)棱鏡桿，每個(gè)時(shí)段觀測(cè)一組平距及豎角值。另外，測(cè)距前需觀測(cè)溫度與氣壓。

(2) 跨海段觀測(cè)

跨海段對(duì)向觀測(cè)采用距離觀測(cè)與豎角觀測(cè)分開進(jìn)行的方式進(jìn)行測(cè)量。在每個(gè)測(cè)量時(shí)段開始之前及結(jié)束之后進(jìn)行距離觀測(cè)，采用正倒鏡測(cè)量的模式，取前后8次測(cè)量的平均值。

豎角的觀測(cè)按照以下步驟進(jìn)行：

1) 在1、2點(diǎn)上分別架設(shè)全站儀進(jìn)行對(duì)向觀測(cè)。按照表1所示的方案進(jìn)行一個(gè)時(shí)段的觀測(cè)。對(duì)向觀測(cè)應(yīng)按照嚴(yán)格的“同步”觀測(cè)進(jìn)行，即1、2點(diǎn)的觀測(cè)間隔限制在5 min之內(nèi)。

2) 若分上下午兩時(shí)段觀測(cè)，則在第二個(gè)時(shí)段開始前重新架設(shè)1點(diǎn)的全站儀(主要是儀器高的改變)，改變對(duì)向觀測(cè)順序，按方案1進(jìn)行觀測(cè)。

為保證時(shí)間上的一致性，最先觀測(cè)的儀器多測(cè)一組，計(jì)算時(shí)，利用舒勒平均值原理，先將最先觀測(cè)的5組兩組之間取平均，然后對(duì)觀測(cè)值取平均。

(3) 過(guò)渡邊對(duì)向觀測(cè)

將1點(diǎn)上的全站儀搬到3點(diǎn)架設(shè)，進(jìn)行2、3點(diǎn)的對(duì)向觀測(cè)，觀測(cè)4個(gè)測(cè)回，對(duì)向觀測(cè)共8個(gè)測(cè)回。變化儀器高，進(jìn)行2、3點(diǎn)間的返測(cè)。

(4) 末點(diǎn)觀測(cè)

將S1上的棱鏡桿移動(dòng)到S2上，保持棱鏡的高度不變，在3點(diǎn)上對(duì)S2進(jìn)行觀測(cè)。在過(guò)渡邊對(duì)向觀測(cè)變化儀器高后，同樣進(jìn)行3、S2點(diǎn)間的返測(cè)。

四、數(shù)據(jù)處理及精度分析

1. 限差分析

根據(jù)《國(guó)家一、二等水準(zhǔn)測(cè)量規(guī)范》(GB/T 12897—2006)的有關(guān)規(guī)定，二等水準(zhǔn)測(cè)量每千米中誤差Mw為2 mm，跨海段的總長(zhǎng)為L(zhǎng)，高差測(cè)量的中誤差應(yīng)不大于

該測(cè)量為8組，取其平均值，則每組測(cè)量的中誤差應(yīng)不大于

兩組之間允許差值(中誤差)為

2. 數(shù)據(jù)分析

項(xiàng)目共進(jìn)行了兩跨海段高程的傳遞，測(cè)段一、二的高差觀測(cè)數(shù)據(jù)見(jiàn)表2。其中，測(cè)段一數(shù)據(jù)為一個(gè)時(shí)段觀測(cè)模式所得；測(cè)段二數(shù)據(jù)分為上、下午兩個(gè)時(shí)段觀測(cè)模式所得。

表2 高差觀測(cè)數(shù)據(jù)

本次測(cè)量中測(cè)段一的長(zhǎng)度為2.469 km，8組高差平均值為-3.449 0 m；測(cè)段二的長(zhǎng)度為1.818 km，8組高差平均值為5.251 1 m。根據(jù)式(4)—式(6)計(jì)算各項(xiàng)限差與實(shí)際值相比較，結(jié)果見(jiàn)表3。

可以看出，測(cè)段一、二不論是高差中誤差還是各組觀測(cè)值間最大互差均小于限差規(guī)定的值，兩個(gè)測(cè)段均達(dá)到二等水準(zhǔn)的要求。

表3 限差與實(shí)際比較 mm

五、結(jié)束語(yǔ)

本文在國(guó)家規(guī)范的基礎(chǔ)上，提出了一種線形觀測(cè)結(jié)構(gòu)，同時(shí)選用高精度的測(cè)量機(jī)器人進(jìn)行相對(duì)嚴(yán)格的對(duì)向觀測(cè)，削弱了大氣折光的影響，采用偶數(shù)站的測(cè)量，避免了量取儀器高和覘標(biāo)高的環(huán)節(jié)，簡(jiǎn)化了作業(yè)流程，提高了作業(yè)效率。最后對(duì)該方法在二等水準(zhǔn)技術(shù)指標(biāo)下進(jìn)行了分析，證明精度達(dá)到二等水準(zhǔn)的要求。

參考文獻(xiàn)：

[1] 李建成，姜衛(wèi)平.長(zhǎng)距離跨海高程基準(zhǔn)傳遞方法的研究[J]. 武漢大學(xué)學(xué)報(bào)：信息科學(xué)版，2001，26(6): 514-517.

[2] 鮑李峰,許厚澤,陸洋,等.利用重力位差實(shí)現(xiàn)跨海高程基準(zhǔn)傳遞：中國(guó)，201110071065.1[P].2011-11-02.

[3] 國(guó)家測(cè)繪局.GB/T 12897—2006 國(guó)家一二等水準(zhǔn)測(cè)量規(guī)范[S].北京:中國(guó)標(biāo)準(zhǔn)出版社,2006.

[4] 潘正風(fēng),楊正堯,程效軍,等.數(shù)字測(cè)圖原理與方法[M].武漢：武漢大學(xué)出版社,2004.

[5] 劉冠蘭,李東宇，丁文宏.精密三角高程測(cè)量在寬水域跨河水準(zhǔn)中的應(yīng)用[J]. 工程勘察,2010，38(10)：71-74.

[6] 王知章,潘正風(fēng),劉冠蘭. 三角高程測(cè)量在高鐵特大橋無(wú)碴軌道施工測(cè)量中的應(yīng)用[J].工程勘察,2009，37(6)：66-68.