立式循環泵轉子系統動態特性分析
王孚懋,劉凱,劉士杰,王昊
(山東科技大學 機械電子工程學院,山東 青島 266590)
0 引言
兗礦集團社區管理中心202水泵房是鐵東社區配套供水系統,該水泵房于2008年進行了擴容改造,水泵運行噪聲對小區居民的生活環境造成了影響,居民反映強烈。泵體噪聲由機械傳動、電機運行和葉輪旋轉等產生,葉輪旋轉產生的低頻振動與空氣噪聲相互耦合,傳播距離遠,影響范圍大,所以研究動力機械設備的低頻振動就顯得尤為重要。
隨著科學技術的不斷進步,現代動力機械設備朝著大型、輕薄、高速、復雜和自動化等方向發展,對動態性能要求愈來愈高。例如,由于機器轉速的提高,使得慣性作用明顯提高,振動與噪聲問題突出,嚴重影響機器的工作性能和使用壽命;由于高速度和輕型化的要求,機構構件彈性變形不可避免,改變了傳統剛性結構的運動與動力性能;由于機器轉速與載荷的增加,使得機構運動副間隙、制造與加工誤差、摩擦、磨損等因素對機器工作性能的影響更加明顯。
針對循環泵振動與噪聲問題,很多學者開展了動力學研究。文獻[1]采用有限元法對離心泵轉子(葉輪及軸)的固有頻率和振型進行了分析和研究,獲得了轉子的固有振動特性及各階臨界速度,與模態試驗的結果相比,在誤差的允許范圍內,證明了有限元建模和計算方法是正確的。文獻[2]將軸承支撐簡化為具有一定剛度的彈簧,用有限元方法計算了曲軸在自由狀態下扭轉和縱向振動的固有頻率,然后計算了不同邊界條件下曲軸的扭轉和縱振固有頻率,通過比較得出了主軸承剛度對曲軸扭轉和縱向振動的影響情況。
本文以換熱站ISG250-315型立式循環泵為例,采用ANSYS有限單元模態分析法,對立式泵自由轉子進行動態分析,同時研究彈性支承剛度對其固有頻率的影響,對泵的設計、減振降噪和安全運行提供理論依據,并結合具體試驗對理論分析進行驗證。
1 有限元結構動態模型
結構模態分析的有限元方法是把物體離散為有限個數量的單元體,考慮粘性阻尼影響,有限元動態方程簡化為一個n自由度的線性定常二階微分方程[3]。

(1)
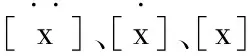
若無外力作用,即:{F(t)} = {0},則得系統的自由振動方程。在求解結構自由振動的固有頻率和振型時,阻尼對它們的影響不大,可以忽略阻尼力對系統的影響,得到自由振動方程如下:
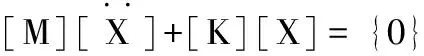
(2)
其對應的特征方程:
(3)
2 剛性支撐轉子模態分析
2.1 轉子實體模型
建立實體模型是為了使模型與真實結構差異盡可能的小,從而使結構比較理想。建立實體模型應依據等效原理對所分析的結構體進行簡化,即對結構體上與分析目標關系不大的部分進行簡化,忽略轉子的過渡圓角、倒角、許多的螺栓聯接孔等,將轉子視為表面分段光滑的筒體結構。采用SolidWorks軟件建成立式泵轉子實體模型,如圖1。
轉子葉輪材料為HT200,彈性模量130GPa,泊松比0.25,密度7800kg/ m3。軸的材料為45鋼,彈性模量200GPa,泊松比0.3,密度7800kg/ m3。
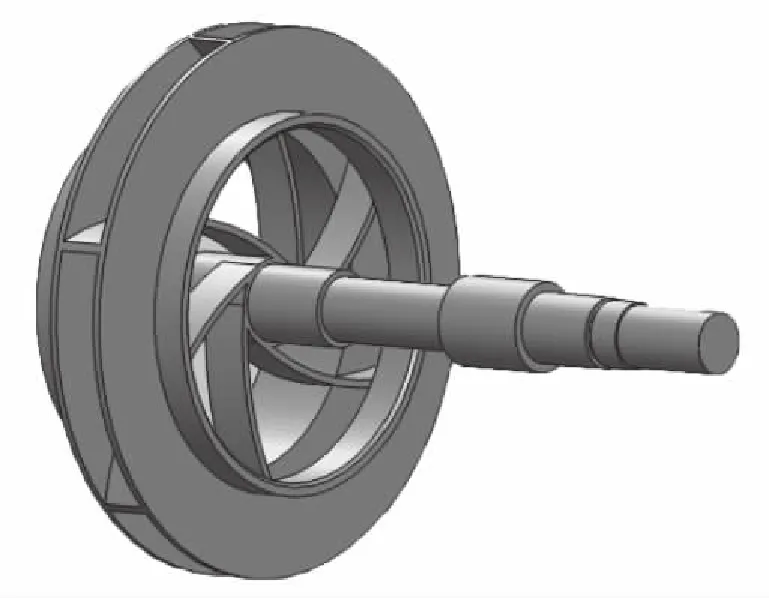
圖1 轉子實體模型
2.2 有限元模型網格劃分
將SolidWorks軟件繪制的泵轉子的三維實體結構模型生成符合Parasolid標準的接口文件,再調用有限元ANSYS軟件進一步分析處理,使用拓撲修復工具來顯示和列出模型中出現的分開和封閉的邊界,并對模型中存在的間隙進行合并造型。在對模型進行網格劃分時,考慮到Solid95單元能夠容忍不規則的網格形狀而保持足夠的精度,故采用20節點四面體Solid95結構實體單元。由于轉子結構的幾何不規則性,采用自由網格劃分,共劃分單元數54892,節點數14160。轉子有限元網格劃分如圖2所示。

圖2 剛性支撐轉子有限元模型
ISG250-315型立式循環泵轉子旋轉頻率為:
電機帶動下的主軸工作轉速1450r/min,得基頻為145Hz,四階轉速頻率為580Hz,七階為1015Hz。從上面的分析可以看出,轉子的一階固有頻率是1529Hz,已經遠高于轉子的工作基頻,所以在運行過程中不會出現轉子結構的低頻共振。
2.3 約束載荷和擴展模態
一般循環泵轉子系統采用滾動軸承的支撐方式,能夠滿足較高的剛度和位移精度的要求。考慮到滾動軸承剛度的不確定性,忽略彈性變形影響,將軸承孔與傳動軸連接視為剛性,軸與軸承的接觸處施加全約束即位移為零[4]。
由于低階模態對剛性支撐轉子系統振動影響較大,設置模態擴展數為6。
2.4 計算結果分析
剛性支撐轉子前6階固有頻率計算結果列入表1,前6階振型見圖3—圖5 。

表1 剛性支撐轉子前6階固有頻率計算結果
由表1可知,剛性支撐下轉子的固有頻率值遠高于轉速頻率,可以有效的避免低頻共振的產生,從而降低了振動的危害性。
由圖3—圖5可以看出,剛性支撐轉子振動表現為彎曲振動和扭轉振動。第一階振型表現為軸的彎曲振動;第三、六階振型表現為葉輪整體受力,葉片受力相對較大,此時軸基本無變形。

圖3 剛性支撐轉子第1階振型

圖4 剛性支撐轉子第3階振型
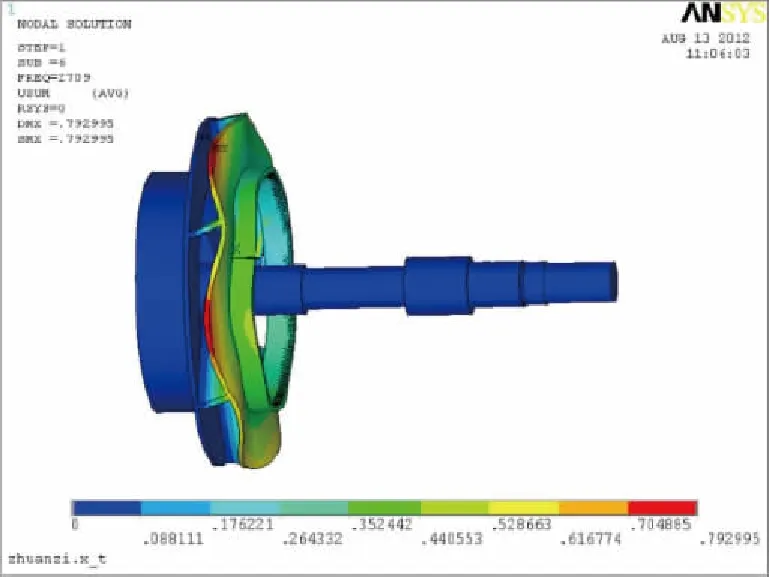
圖5 剛性支撐轉子第6階振型
3 彈性支撐轉子模態分析
3.1 滾動軸承簡化力學模型
以上對剛性支撐轉子進行了模態分析,考慮到難以確定滾動軸承的剛度,所以將軸承孔與傳動軸連接視為剛性,但是在實際應用中,滾動軸承支座并不是完全剛性的,需要考慮軸承的彈性影響。滾動軸承的彈性支撐簡化力學模型如圖6所示。
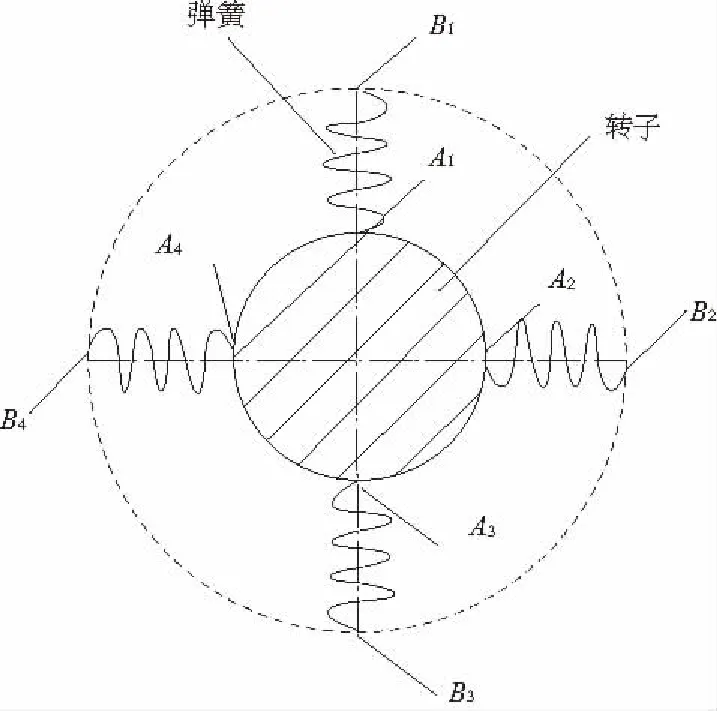
圖6 滾動軸承的簡化力學模型
在圖6中,用均布的四個彈簧等效軸承的彈性支撐,其中A1,A2,A3,A4,為傳動軸上的節點,分別與軸承底座連接點處的B1,B2,B3,B4,四個節點一一對應。采用ANSYS中的Combin14單元對4個假設的均布彈簧進行網格劃分,該單元由兩端節點定義,適用于一維、二維或三維空間的縱向或扭轉振動。不計彈簧的單元質量,也不考慮彈簧彎曲及扭轉,每個節點具有x、y和z三個方向的位移。Combin14模擬彈簧單元限制了轉子在主軸x方向的移動,A1,A2,A3,A4,四個節點處加上彈性約束,在另一端B1,B2,B3,B4,四個節點為完全固接。
3.2 軸承彈性支撐對轉子系統動態特性影響
為了保證轉子工作轉速符合設計要求,需要研究彈性支撐轉子固有特性的影響。以ISG250-315型立式循環泵為研究對象,改變彈簧單元Combin14的剛度計算轉子相應的固有頻率,對比剛性約束的結果分析其影響規律。通過以下經驗公式計算軸承的徑向剛度[5],即:
式中:d1——鋼球直徑;R——徑向載荷;
Z——滾子數目;β——滾動體接觸角。
由此可以計算出軸承剛度K:
9.7×105kN/m
兩個軸承相互排列,平均承受徑向載荷,所以總剛度為:2×9.7×105=1.94×106kN/m。研究滾動軸承的彈性支撐剛度范圍選為(106~107)kN/m。支撐剛度對轉子系統固有頻率的影響計算結果如表2所示。
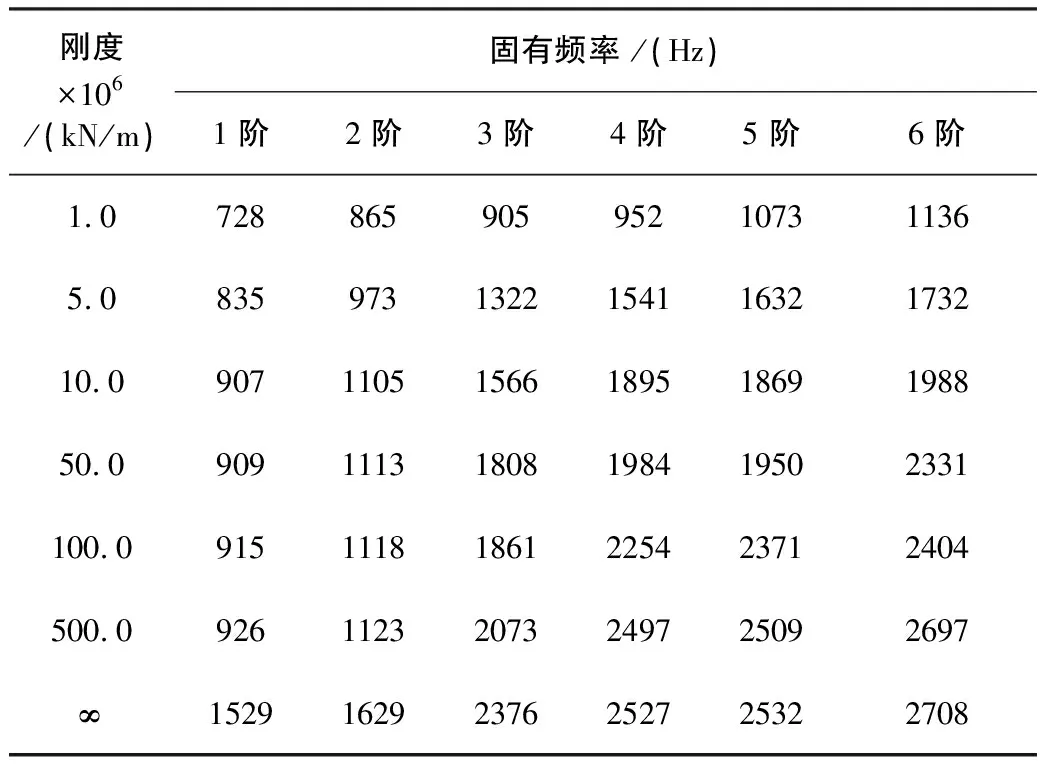
表2 支撐剛度對轉子系統固有頻率的影響
由表2可以得出,彈性支承作用下,轉子系統的固有頻率要比剛性支撐下的固有頻率低,而且隨著彈簧剛度的不斷增加,兩種支承方式下的固有頻率值逐漸接近。如圖7所示,根據表2數據繪制前兩階固有頻率隨支撐剛度變化的曲線。
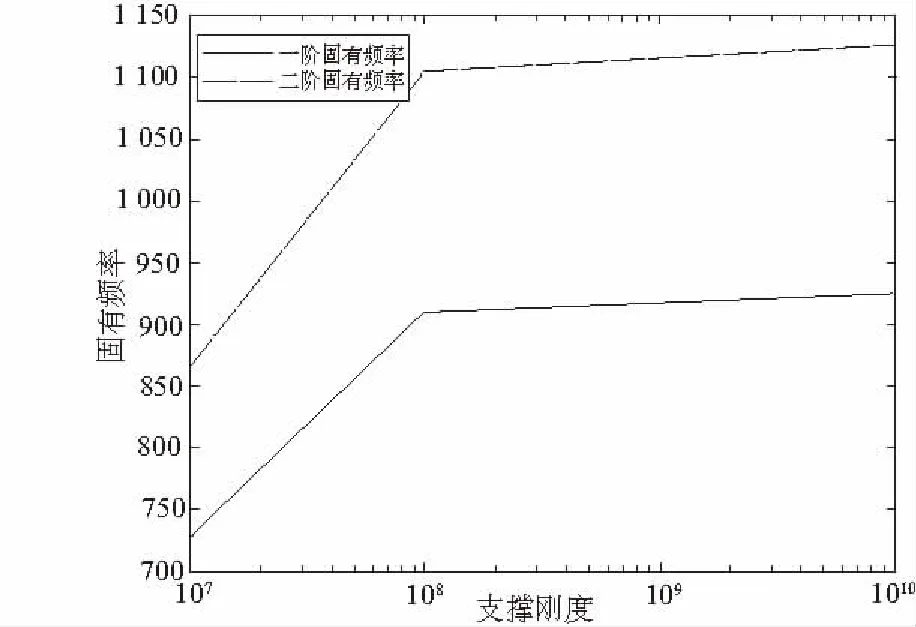
圖7 前兩階固有頻率隨剛度變化規律
4 試驗
4.1 LMS Test.Lab測試系統簡介
試驗采用比利時LMS公司的LMS Test.Lab模態、振動、噪聲測試分析系統對泵的轉子系統進行測試與分析。LMS Test.Lab是一整套的振動噪聲試驗解決方案,是高速多通道數據采集與試驗、分析、電子報告工具的結合,包括數據采集、數字信號處理、結構試驗、旋轉機械分析、聲學和環境試驗。同時它也是一個應用開發平臺。
4.2 試驗操作過程和結果
具體做法如下:將壓電式加速度傳感器分別安裝在轉子軸承接觸處某一測點的x、y、z方向(以被測泵體的進出水口方向為x方向,以上下方向為y方向,另一方向為z方向),傳感器的輸出經電荷放大器放大后輸入LMS SCADASIII多通道數采前端,計算機通過軟件系統分時對3個參數進行采集,現場對各測點進行動態分析,作出響應的時間波形,分析得振動加速度頻率圖(圖8)。
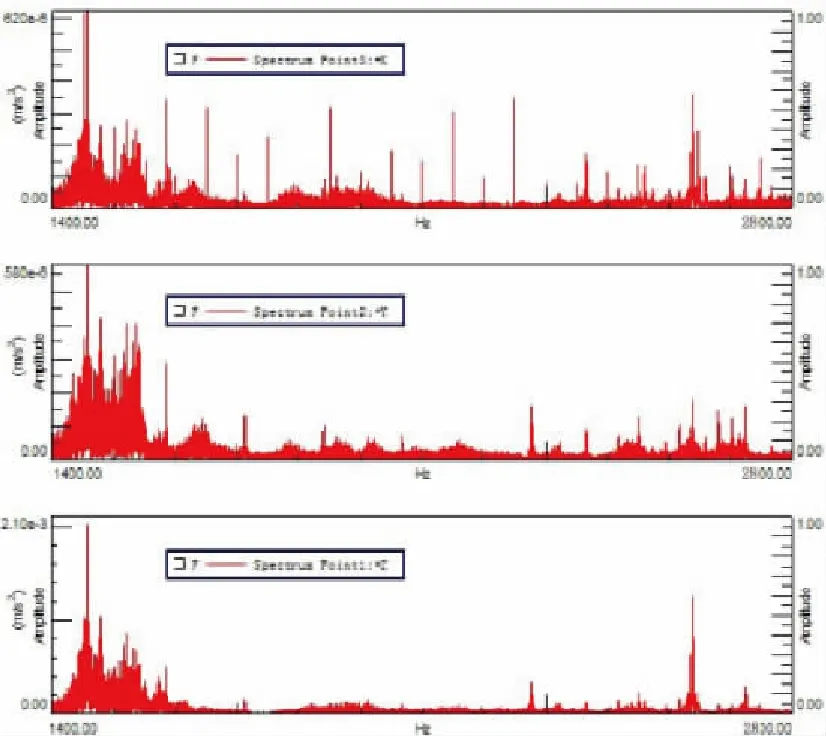
圖8 測點的三個方向振動加速度

通過試驗結果發現泵的主振動方向為x和y方向。將理論研究固有頻率值與實驗研究的進行對比(表3),理論分析結果和試驗結果基本一致,增強了理論研究的可操作性。
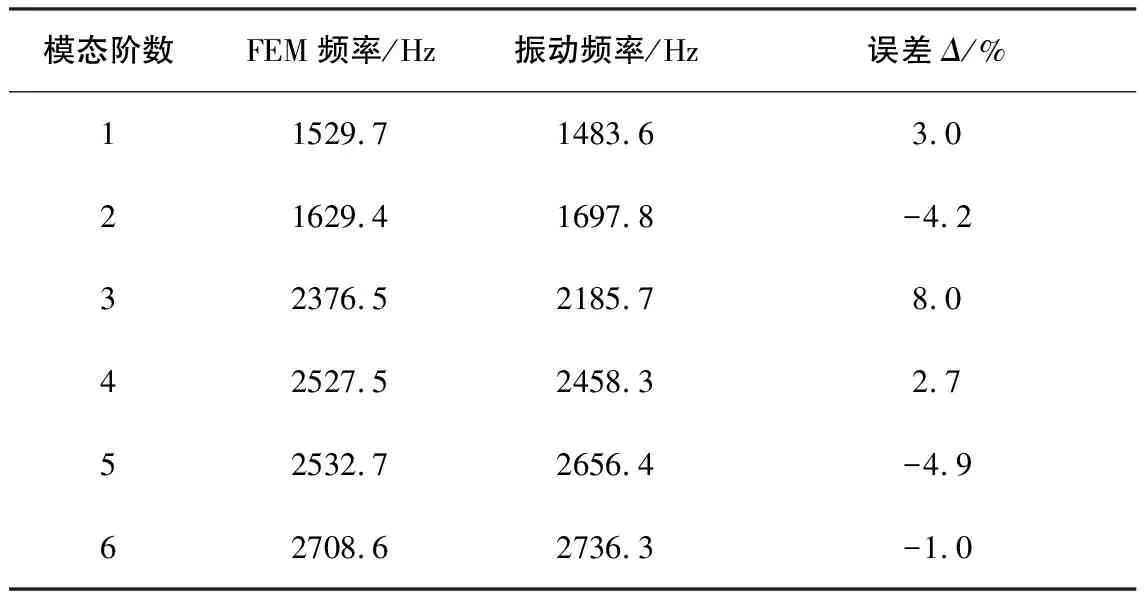
表3 試驗立式循環泵的前六階固有頻率
5 結語
1) 把軸承看作彈性支撐時,轉子系統的低階固有頻率顯著降低。通過改變彈性單元剛度對轉子進行模態分析,得出軸承剛度對固有頻率的影響,對轉子的設計有重要指導意義。
2) 一般轉子的彈性支撐剛度約為106~107kN/m,此時泵轉子固有頻率遠高于轉子的工作轉速,符合設計要求。
3) 基于ANSYS有限元技術的立式循環泵轉子系統動態計算與設計,方法簡便,節省時間,便于與泵整機動態分析與結構設計接口,為泵的整機設計與模態分析提供理論基礎。
4) 采用試驗法,驗證理論分析結果正確性,使研究具有一定的理論水平和實際應用價值。
[1] 于敏保,黃站立.離心泵轉子的有限元模態分析[J].機械工程師,2005(6):108-109.
[2] 郝志勇,韓松濤.主軸承剛度對曲軸振動特性影響的研究[J].車輛與動力技術,2001,82 (2):31-35.
[3] 高翔,胡淼.框架式熱壓機機架有限元分析及結構優化設計[J].機械設計,2009(2):62-64.
[4] 李潤方,林騰蛟,陶澤光.齒輪系統耦合振動響應的預估[J].機械設計與研究,2003,19(2):27-29.
[5] 魏彬,李建華,鄧四二.滾動軸承-轉子系統動力學特性分析[J].軸承:2012,10(6):1-6.

