基于有限元的炮尾結構優化設計

付帥，顧克秋，張俊飛

(南京理工大學 機械工程學院, 江蘇 南京 210094)

0 引言

火炮在實際中的工況極其惡劣，其在發射過程中，閂體會承受較大的膛底壓力，炮尾承受和傳遞閂體所受到的作用力，因此在炮尾的內部和閂體相接的圓角處，就會造成較大的應力集中，因而炮尾在圓角處會發生疲勞裂紋。

以往相關的研究都是給出理論降低圓角應力的方法，隨著計算機技術的發展和相關軟件的進步，使得利用計算機計算解決炮尾圓角問題成為一種可能。本文以某一種降低炮尾圓角應力的方法為對象，利用二次編程技術，進行有限元分析設計，并通過集成ISIGHT優化軟件，尋找最優參數。這不僅可以為用其他方法降低圓角應力提供參考，還能較好的解決以前受技術限制的炮尾問題。

1 炮尾模型

1.1 炮尾模型中的應力集中問題

由于火炮發射時，膛壓對閂體產生較大的作用力，炮尾用于傳遞和抵消這些作用力，對于滑動閂體的火炮，炮尾的破壞往往從與閂體接觸區近鄰的炮尾圓角開始[1]。在炮尾圓角處首先產生一些微小的裂痕，進而整個炮尾從中斷裂開，對炮尾結構造成惡劣破壞。

以某大口徑火炮的炮尾為例，傳統的三維炮尾模型如圖1[2]，二維炮尾模型尺寸如圖2所示(只給出一半的尺寸)，由于實際炮尾縱向尺寸變化很小，可以用平面模型代替三維模型，這樣不僅可以降低模型的復雜程度，還能節省計算時間，試驗結果和實際結果也較為接近。利用有限元軟件進行分析，設置最大膛壓為396.96MPa，畫網格時使的網格疏密得當，得出應力云圖如圖3，發現在炮尾圓角處的應力為2641MPa。

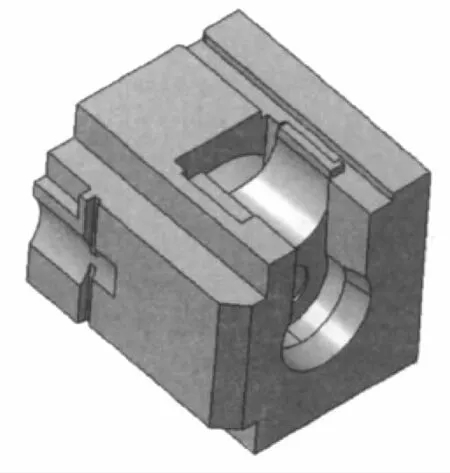
圖1 三維炮尾模型

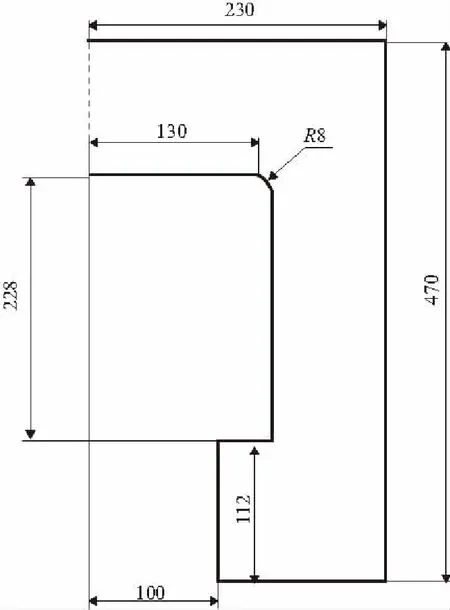
圖2 二維炮尾模型尺寸

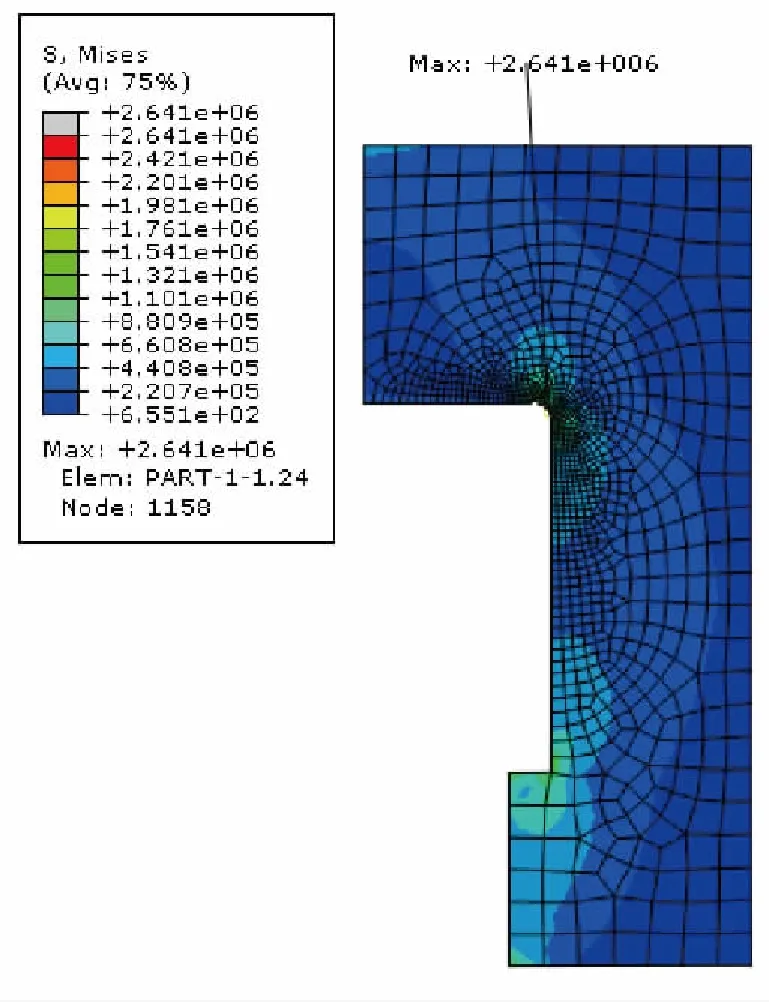
圖3 有限元計算結果

因此，解決炮尾圓角應力問題，可以大大提高火炮的安全性和使用性。

1.2 炮尾圓角

目前，火炮中使用較多的炮尾圓角有以下三種。這三種炮尾圓角都可以有效的降低炮尾圓角應力，如圖4。

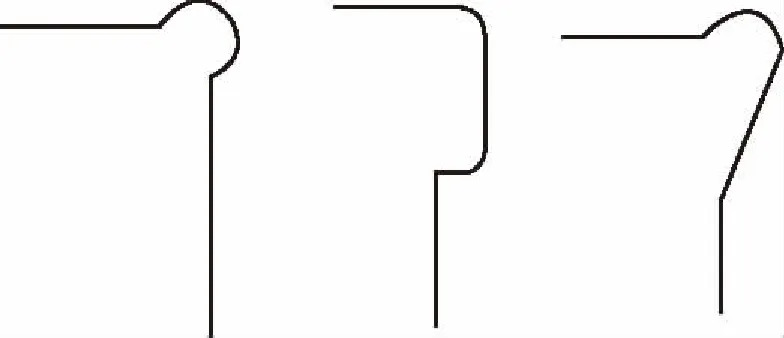
圖4 三種不同的圓角

合理的選擇圓角形狀，可以較好的減小集中應力，但是無法大幅度的減小集中應力；再選擇合理的炮尾結構，可以進一步減小集中應力。本文選擇階梯炮尾結構，結合圖4所示的第一個炮尾圓角進行優化，尋找可以得到最小圓角應力的參數。

2 炮尾圓角優化設計

2.1 NSGA—II算法原理[3]

NSGA—II算法中沒有外部檔案，而是在每一代，首先對種群P進行遺傳操作，得到種群Q，然后將兩種群合并后，進行非劣序和擁擠距離排序，形成新的種群P，反復進行直到結束。NSGA—II是NSGA的改進版本，于2002年提出。

NSGA—II的具體過程描述如下：

1) 隨機產生初始種群P0，然后對種群進行非劣排序，每個個體都被賦予秩；再對初始種群執行二元錦標賽選擇、交叉和變異，得到新的種群Q0，令t=0。

2) 形成新的群體Rt=Pt∪Qt，對種群Rt進行非劣排序，得到非劣前端F1，F2，…。

3) 對所有Fi按擁擠比較操作n進行排序，并選擇其中最好的N個體形成種群Pt+1。

4) 對種群Pt+1執行復制、交叉和變異，形成種群Qt+1。

5) 如果終止條件成立，則結束；否則，t=t+1,轉到2)。

其主要過程如圖5所示。

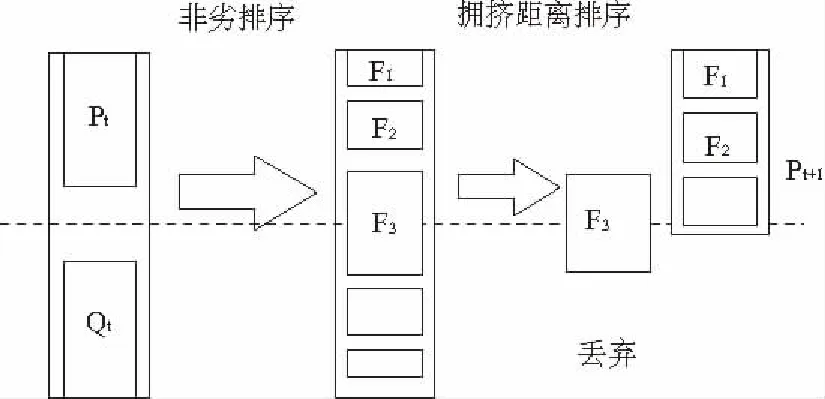
圖5 NSGA—II的主要過程

2.2 臺階炮尾的工作原理

火炮發射時，膛底壓力對藥筒作用，閂體提供一個擋體，阻擋藥筒的后移趨勢，這樣，閂體就會對炮尾產生作用力。采用臺階式炮尾結構，如圖6，閂體勢必會和炮尾的兩個臺階面接觸，如果B面和閂體沒有間隙，隨著膛壓的增加，則B面首先全部受力，受到的載荷較大，A面承受較小的載荷；如果B面和閂體的間隙過大，則B面基本不受力，A面承擔了全部的載荷；如果B面和閂體的間隙合理，當膛壓增加到一定值時間隙消失，繼續增加到最大值時，A、B面處可以相等分擔載荷[4]。所以，選擇合適的B面與閂體的間隙，能夠很好的控制圓角應力，使其處于合理的范圍之內。

2.3 參數化建模

由于模型中有兩個臺階，所以必然會出現兩個圓角。圓角處的應力是本文優化的目標，故每個圓角處的變量有3個：圓角圓心和上階面的距離X，圓角圓心和側面的距離Y，圓角半徑R和閂體上臺階面到閂體下臺階面的距離L。炮尾模型中共有7個變量，優化模型如圖6，圓角放大圖模型如圖7。對應的臺階閂體二維優化模型如圖8所示。另外，臺階式炮尾優化模型的尺寸參數取值范圍如表1所示。

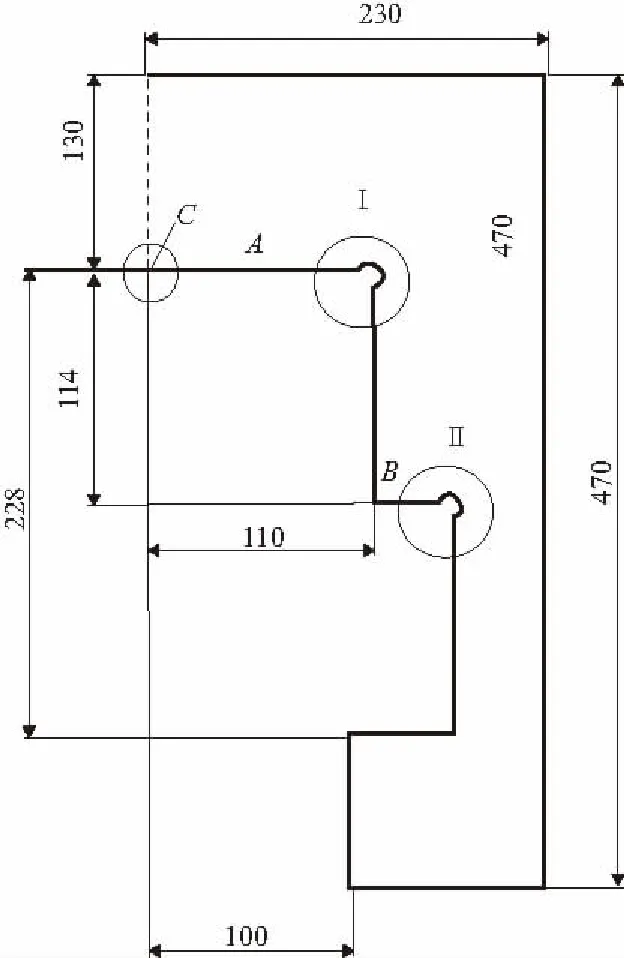
圖6 臺階式二維炮尾優化模型尺寸

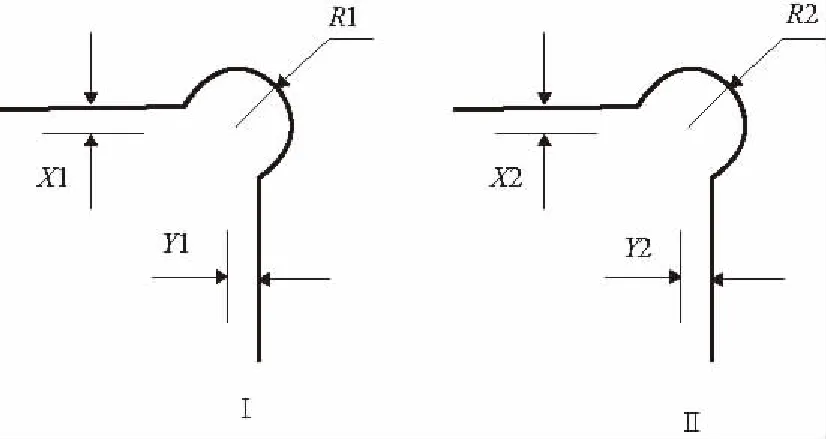
圖7 圓角放大圖模型

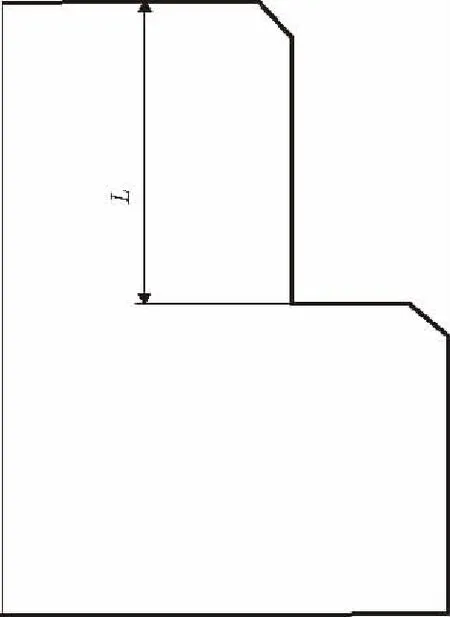
圖8 臺階閂體模型

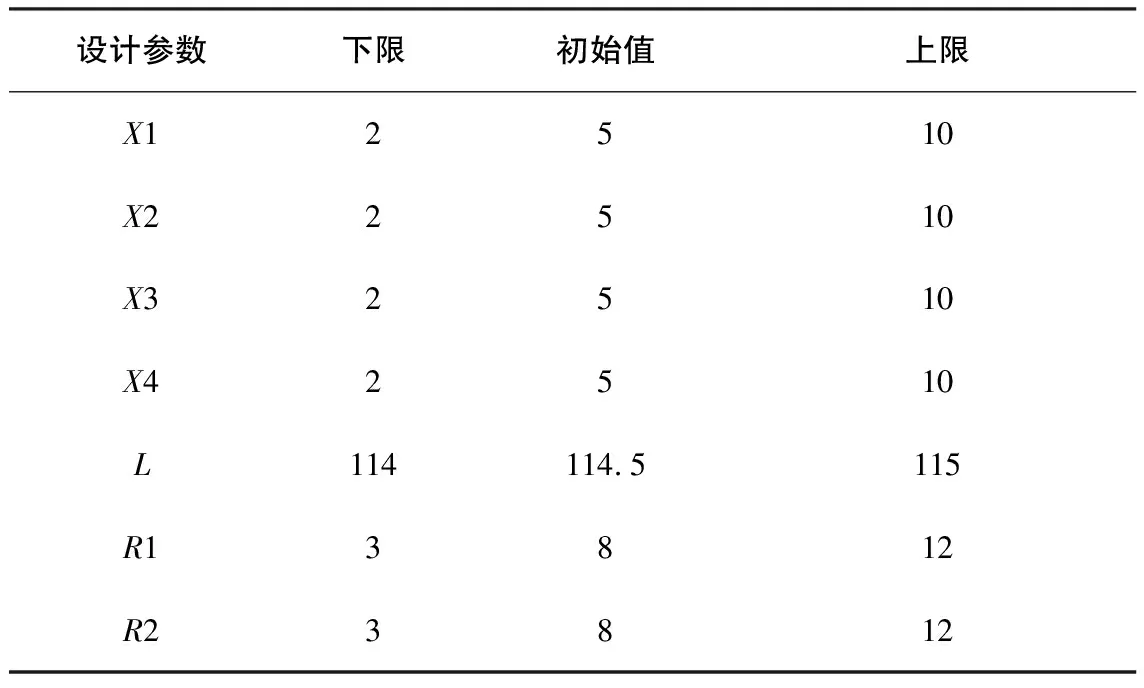
表1 優化模型尺寸參數取值范圍 mm

參數化建模，可以有效的減少人員操作的時間，大大提高了優化效率。建立參數化模型，可以通過編寫Python腳本文件，實現ABAQUS的二次開發，控制ABAQUS的自動前處理和后處理分析結果[5]。在ABAQUS中建模，模擬閂體受力和約束情況，施加相應的載荷，生成炮尾結構的有限元模型文件，并且設置變量，使得在每一次運行炮尾結構有限元模型文件時，模型都會隨著變量的改變而改變，不需要人為的更改模型尺寸而進行計算。同時，還可以設置對應的輸出變量，能夠直觀的看到結果。

在模型中，為了能夠保證得到圖7中的圓角，則只需要滿足公式X-R≤0,Y-R≤0，即可實現。另外，模型中的長度單位為mm，對應的應力單位為MPa，考慮到圓角工藝，對R取整數值，此外，本模型有3個優化目標，分別為A面的應力Ma，B面的應力Mb和λ，其中λ為A面的應力和B面的應力之比再減去1。從而得到炮尾結構的優化數學模型：

2.4 優化流程

可用于優化的軟件有很多，本文選用ISIGHT優化軟件作為處理多目標優化問題的軟件，再集成ABAQUS有限元分析軟件，對模型進行分析計算。編寫ABAQUS的腳本控制文件，每次提交模型文件時，都會得到相應的結果，通過ISIGHT自動判斷是否符合最優解，按照設定的迭代次數，完成優化任務。優化流程圖如圖9。

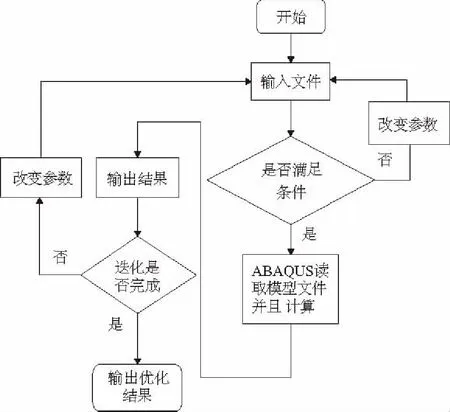
圖9 優化流程圖

3 圓角應力優化結果分析

如果不考慮圓角半徑R和圓心與兩邊的距離X,Y的影響，單一的優化閂體上臺階面到閂體下臺階面的距離L，肯定可以找到一個值，使得兩個臺階處的圓角應力相當。以初始模型的圓角半徑和圓心位置X，Y為例，X=Y=5mm，R=8mm，通過簡單計算，當兩臺階處的圓角應力相當時，閂體上臺階面到閂體下臺階面的距離L=114.4154mm。

本文為了簡單起見，在一定位移的條件下進行優化，就是說，在滿足了一定的剛度的情況下進行優化計算，即，給出三種C點處位移U(如圖6所示)的上限值進行優化分析，這四種位移條件分別為：U≤1.6mm，U≤1.5mm，U≤1.4mm。

本文采用NSGA—II優化方法，并對目標函數進行加權，把多目標優化轉變成單目標優化。通過計算分析，得到近似最優解，和初始數據比較，如表2所示。三種情況下的圓角應力和位移U如表3所示。

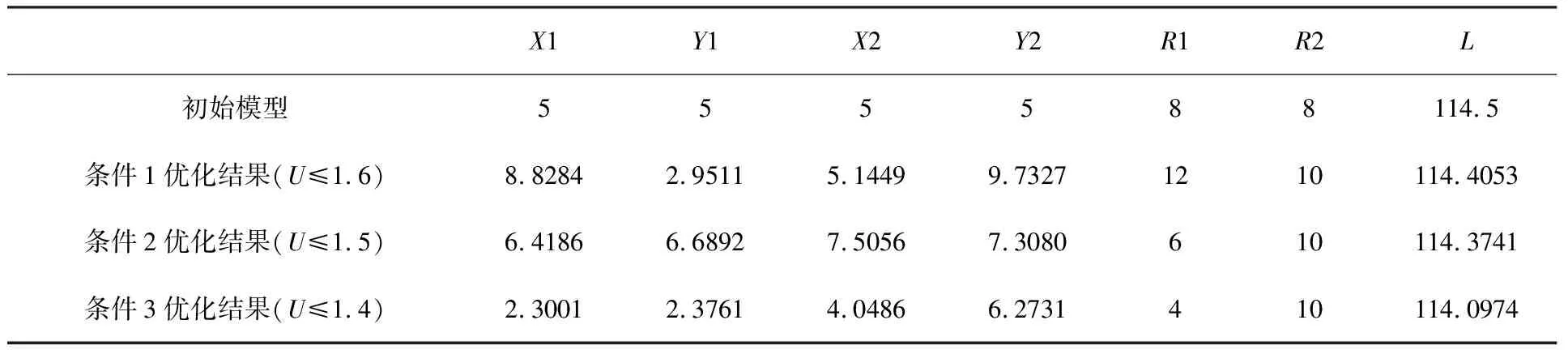
表2 優化結果 (單位：mm)

表3 應力值、位移值的比較

4 結論

由于炮尾尺寸和膛底壓力給出的隨意性，圓角應力值高于實際材料的屈服極限，本文不考慮實際材料，旨在尋求一種降低圓角應力的方法。

由優化結果和應力值、位移值比較分析可得，在條件1情況下，由于U最大可達到1.6mm，所以，圓角的應力相對較小，約為1750MPa，但圓角半徑相對較大，與初始模型比較，位移U相差不大，但圓角應力最大可降低557.577MPa；在條件2情況下，位移U的最大值是1.5mm，與初始模型相比，臺階A處圓角應力降低251.811MPa，臺階B處圓角應力基本沒變；在條件3情況下，位移U的最大值是1.4mm，該組優化結果和條件2相比較，A處圓角半徑較小，但應力結果和條件2基本相同。

據此可以看出，采用臺階式炮尾，控制臺階B處閂體和炮尾的間隙，可以明顯的改變應力分布，降低應力值，同時對圓角半徑和圓心位置優化，可以進一步的降低圓角應力。

[1] 孫遠孝,徐振翔.炮尾圓角應力集中問題的分析[J].兵工學報，1993,4:11-16.

[2] 項立銀,顧克秋.基于響應面法炮尾炮閂6σ穩健優化設計[J].機械制造與研究，2011，20-22,48.

[3] 雷德明,嚴新平.多目前只能優化算法及應用[M].北京：科學出版社，2009(1):47.

[4] 顧克秋.具有臺階式門室的炮尾結構原理[J].火炮發射與控制學報，1995,3:29-32.

[5] 彭迪,顧克秋.基于響應面法的三維炮尾結構設計優化[J].計算機輔助工程，2010,19(4):91-94,98.