基于價(jià)格和銷售努力補(bǔ)貼的庫存模型

葛安華，苑文雅，白曉宇

(東北林業(yè)大學(xué) 工程技術(shù)學(xué)院，哈爾濱 150040)

在經(jīng)濟(jì)快速發(fā)展競爭激烈的環(huán)境下，經(jīng)典庫存控制EOQ模型不能完全適用于現(xiàn)在的市場需要。對市場的調(diào)查研究可以發(fā)現(xiàn)銷售商所確定的銷售價(jià)格和銷售努力投入對市場的需求具有決定性的影響，同時(shí)越來越多的銷售商意識到只有與供應(yīng)商有效合作才能達(dá)到雙贏。Kunreuther和Richard[1]第一次從定量的角度建立需求受價(jià)格影響的最優(yōu)訂購批量以及最優(yōu)銷售價(jià)格的數(shù)學(xué)模型；Baker W[2]和Huang Z[3]以廣告作為促銷手段建立供應(yīng)商和銷售商之間的供貨模型；周永務(wù)[4]、汪峻萍[5]在考慮價(jià)格與廣告投入費(fèi)用的前提下，建立了商品的最優(yōu)廣告投入與訂貨策略的隨機(jī)模型；胡本勇[6]、李清艷[7]在研究收益共享和銷售努力成本共擔(dān)的供應(yīng)鏈模型中，分析了銷售努力共擔(dān)對供應(yīng)鏈的協(xié)調(diào)的影響。

雖然許多研究者針對不同的合作問題建立了需求與價(jià)格、銷售努力等相關(guān)的分析模型，但是在批量折扣前提下，把銷售價(jià)格、銷售努力以及供應(yīng)商共擔(dān)的銷售努力補(bǔ)貼同時(shí)引入進(jìn)行決策的卻很少。本文以價(jià)格和銷售努力決定的需求函數(shù)為前提，引入供應(yīng)商提供的銷售努力補(bǔ)貼，建立銷售商最優(yōu)的定價(jià)訂貨模型，以達(dá)到利潤最大化。最后通過數(shù)值實(shí)例對模型進(jìn)行驗(yàn)證。

1 銷售商依賴價(jià)格和銷售努力補(bǔ)貼的庫存模型

1.1 參數(shù)意義與模型假設(shè)

(1)參數(shù)意義見表1。

(2)模型假定：①假設(shè)系統(tǒng)在無限周期水平上運(yùn)行并且不允許缺貨，補(bǔ)充缺貨瞬時(shí)完成；②邊際收入d(pD)/dD=p+D/D′是關(guān)于p的增函數(shù)[8]，對于任意的p，都存在2-(DD″/D′2)>0。

表1 參數(shù)意義

1.2 模型建立

最優(yōu)庫存控制的決策問題可以轉(zhuǎn)化為存在批量折扣的情況下，如何確定最優(yōu)的銷售價(jià)格、訂購量以及最優(yōu)銷售努力投入[9]，從而使銷售商在一個(gè)周期內(nèi)的平均總利潤達(dá)到最大。

1.2.1 需求函數(shù)的確定

銷售努力投入越多，就有越多的顧客了解其經(jīng)銷商品和經(jīng)營場所的有關(guān)情況，因而對其經(jīng)銷商品的需求量就越大。但不能無限制增長，其遞增效用會(huì)逐漸減弱，最終趨于零。在保證銷售價(jià)格不變的前提下，受銷售努力影響的增加的需求量為D(I)=αIβ[7]，此函數(shù)應(yīng)用較為廣泛更符合實(shí)際。α為促銷投資系數(shù)，β為投資的彈性，由于邊際效用是逐漸遞減的，所以0<β<1 。

綜合考慮需求受價(jià)格和銷售努力的影響，則需求函數(shù)為D=f(p，I)=a-bq+αIβ(以下簡稱為D)。

1.2.2 供應(yīng)商的批量折扣

在實(shí)際中，銷售商單位產(chǎn)品的購進(jìn)價(jià)是與其訂購批量緊密聯(lián)系的，訂購批量越大，訂購進(jìn)價(jià)相應(yīng)的減少，即批量折扣。考慮到簡化模型，本文采用符合實(shí)際且運(yùn)用廣泛的全單位量折扣[4]，模型如下：

式中：c0>c1>…>cm。

1.2.3 模型的建立

一個(gè)周期內(nèi)銷售商所獲得的平均總利潤，與銷售收益R、購買費(fèi)用Cp、庫存費(fèi)用Ch、訂購費(fèi)用C0以及銷售商努力投入CI有關(guān)，是I、p、Q的函數(shù)，記為G(I，p，Q)(以下簡稱為G)。其中，R是指企業(yè)在一定時(shí)期內(nèi)銷售產(chǎn)品的貨幣總收入，R=pD。Cp是指支付給供應(yīng)商的所購物品的費(fèi)用，Cp=cD。Ch是指貨物入庫到出庫過程中用于物品保管的所有費(fèi)用，可以簡單地用單位產(chǎn)品在單位時(shí)間內(nèi)庫存持有成本占銷售商單位購買成本的百分比來計(jì)算，Ch=Qhc/2。C0是指銷售部門每訂購一次貨物所發(fā)生的費(fèi)用，該項(xiàng)費(fèi)用只與訂購的次數(shù)有關(guān)，C0=AD/Q。CI是指在一個(gè)銷售周期內(nèi)，銷售商為了促進(jìn)商品銷售所做的投入，本文考慮供應(yīng)商向銷售商提供的銷售努力補(bǔ)貼，則銷售商實(shí)際所做的銷售努力投入為CI=λID/Q。

(1)

根據(jù)一階最優(yōu)性條件可得，最優(yōu)的p*需滿足下式：

(2)

再求G在p=p*的二階偏導(dǎo)得，

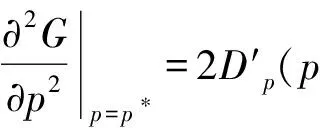
同理最優(yōu)的I*需滿足下式，

(3)

再求G在I=I*的二階偏導(dǎo)得：

(4)

將函數(shù)D(I*，p)=a-bp+α(I*)β帶入公式(4)化簡得：

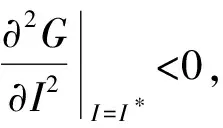
因此，對于確定的訂購批量Q，帶入公式(2)和(3)求得p*和I*實(shí)際上是關(guān)于Q的函數(shù)，即p*=p*(Q)，I*=I*(Q)。將p*和I*帶入式(1)，那么銷售商的平均總利潤可以表示為只關(guān)于Q的一元函數(shù)，不妨記為G(p*，I*，Q)=G1(Q)。然后，求最優(yōu)訂購批量Q*使G1(Q)取得最大值。

根據(jù)一階最優(yōu)性條件可得，最優(yōu)的Q*需滿足下式：

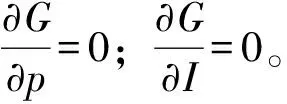
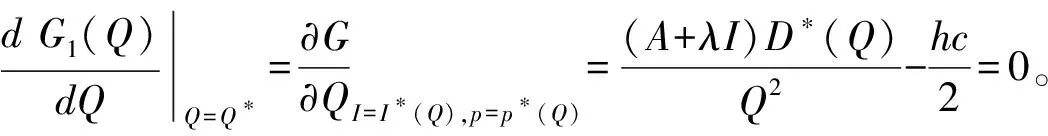
(5)

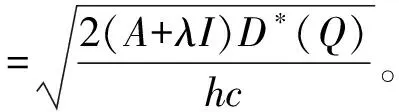
把函數(shù)D(I，p)帶入(2)、(3)、(5)整理并化簡得方程組：

(6)

2 實(shí) 例

以哈爾濱市大型超市家樂福所銷售的維達(dá)四層薄荷手紙帕為例。經(jīng)過調(diào)查發(fā)現(xiàn)家樂福銷售的同類產(chǎn)品大約有10余種，每種又有不同的系列，價(jià)位在3～11元/條不等，同類產(chǎn)品之間可替代性強(qiáng)，需求價(jià)格彈性較大。根據(jù)以往的銷售記錄，利用多元回歸分析的方法預(yù)測需求函數(shù)為D(p，I)=3600-400p+500I0.2。每次訂購該商品需要的固定訂購費(fèi)用為A=200元，單位產(chǎn)品在單位時(shí)間內(nèi)平均庫存持有成本占零售商單位購買成本的百分比為h=40%，供應(yīng)商對銷售商所做的銷售努力補(bǔ)貼率，則λ=1-s=0.8。供應(yīng)商提供的全單位數(shù)量折扣如下：

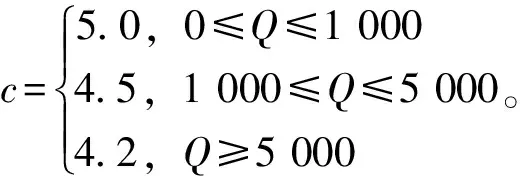
考慮銷售努力投入時(shí)，將所有已知的參數(shù)帶入公式(6)中，利用matlab軟件可算出不同訂購價(jià)格下銷售商的最優(yōu)訂購量、銷售價(jià)格及銷售努力投入見表2。

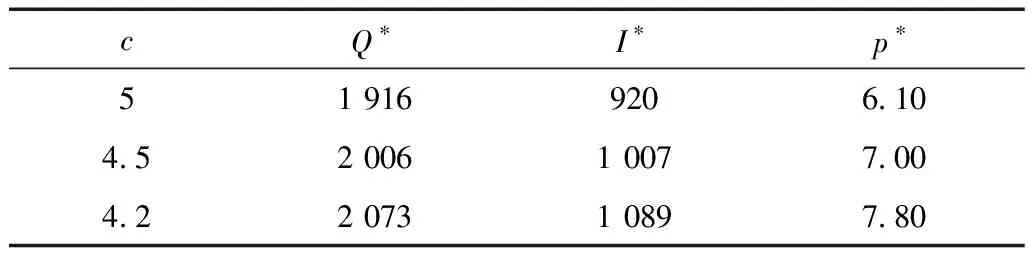
表2 計(jì)算結(jié)果

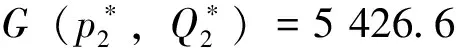
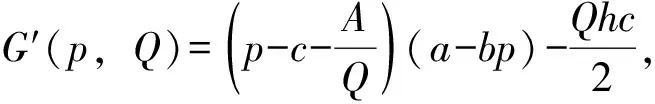
可以看出，在給定的數(shù)值條件下，考慮銷售努力和不考慮時(shí)最優(yōu)銷售價(jià)格相差不大，但是大大提高了訂購批量，從而驗(yàn)證銷售努力促進(jìn)商品的銷售，提高銷售商的平均總利潤。

3 結(jié) 論

在批量折扣情況下，建立了由一個(gè)供應(yīng)商和一個(gè)銷售商組成的銷售努力共擔(dān)的庫存控制模型。運(yùn)用線性需求函數(shù)，并引入銷售努力以及銷售努力補(bǔ)貼更加貼近現(xiàn)實(shí)的市場運(yùn)營形式。不同于傳統(tǒng)的庫存控制只確定最優(yōu)訂購批量，還確定了最優(yōu)銷售價(jià)格和銷售努力水平。并通過實(shí)例進(jìn)行驗(yàn)證，最后證明銷售商平均總利潤明顯增加。

【參 考 文 獻(xiàn)】

[1] Kunreuther H，Richard J F.Optimal pricing and inventory decisions for non-seasonalitems[J].Ecnometrica，1971，39(1)：173-175.

[2] Baker W，Marn M，Zawada C.Price smarter on the net[J].Harvard Business Review 2001，79(2)：122-127.[3] Huang Z，Li S X.Co-op advertising models in a manufacturer retailer supply chain：A game theory approach[J].European Journal of Operational Research，2001，135(3)：52-544.

[4] 周永務(wù).庫存控制理論與方法[M].上海：科學(xué)出版社，2009.

[5] 汪峻萍，周永務(wù)，楊劍波.需求依賴廣告費(fèi)用和銷售價(jià)格的 newsboy 型產(chǎn)品庫存模型[J].控制與決策，2010，25(1)：89-92.

[6] 胡本勇，王性玉.考慮努力因素的供應(yīng)鏈?zhǔn)找婀蚕硌莼跫s[J].管理工程學(xué)報(bào)，2010，24(2)：135-138.

[7] 李清艷.需求依賴銷售努力和銷售價(jià)格的庫存模型[D].合肥：合肥工業(yè)大學(xué)，2011.

[8] 克里斯托弗.R托馬斯.管理經(jīng)濟(jì)學(xué)第九版[M].北京：機(jī)械工業(yè)出版社，2009.

[9] 楊英姿，楊慧敏，王 雨.基于RFID技術(shù)的現(xiàn)代倉儲管理優(yōu)化設(shè)計(jì)[J].森林工程，2013，29(3)：115-117.

[10] 高鴻業(yè).西方經(jīng)濟(jì)學(xué)[M].北京：中國人民大學(xué)出版社，2007.