德薩格定理與點共線及線共點問題
黃振華
(湖北師范學院 數學與統計學院, 湖北 黃石 435002)
德薩格定理與點共線及線共點問題
黃振華
(湖北師范學院 數學與統計學院, 湖北 黃石 435002)
德薩格定理及其逆定理是證明“點共線”和“線共點”問題實用性很強的理論工具,討論了在“點共線”和“線共點”問題中應用德薩格定理及其逆定理的基本方法與思想。
德薩格定理;點共線;線共點;無窮遠元素
高等幾何是高等師范類院校數學與應用數學專業的一門重要專業基礎課程,對初等幾何的教學與研究能居高臨下地具有高觀點的指導作用和意義。德薩格(Desargues)定理是高等幾何課程中的一個重要的定理,德薩格定理的內容從完整的角度講,包括德薩格定理及其逆定理;是證明“點共線”和“線共點”問題的理論工具。然而,實際教學中發現,許多同學在學習德薩格定理時,應用起來常常遇到這樣或那樣的困難,針對這一問題,將對如何正確靈活地應用德薩格定理及其逆定理作幾點探討。
1 德薩格定理及應用的基本思想
1.1德薩格定理
德薩格定理[1]如果兩個三點形對應頂點的連線交于一點,則對應邊的交點在一直線上。
德薩格定理的逆定理[1]如果兩個三點形對應邊的交點在一直線上,則對應頂點的連線交于一點。
1.2德薩格定理應用的基本思想
對于解決“點共線”和“線共點”問題的有力工具德薩格定理和它的逆定理,在應用上,具有同樣重要的地位和作用。定理本身的條件和結論都十分簡明,但在應用中的靈活性很大。有些同學在遇到有關問題時往往無從下手,主要是兩個對應三點形的選取上存在一定的難度。正確地確定滿足定理條件且符合所證命題結論的兩個對應三點形,是解決問題的關鍵。由于使用定理的角度和出發點不同,從而導致選取對應三點形的不同,具體思路可有以下兩種情形。
1)對于三點共線問題,可選用兩個解決方式,一是把三點看成兩個對應三點形的對應邊的交點;二是把三點中的兩點看成是兩個對應三點形的一對對應頂點(可作為一條連線看待),剩余的一點看成是另外兩對對應頂點連線的交點。顯然,前者用德薩格定理,后者用德薩格定理的逆定理。
2)對于三線共點問題,解決此類問題可把三線看成三條線段,也有可選用的二個方式,一是把三條線段分別看成兩個對應三點形的對應頂點的連線,而對應頂點就是每條線段的兩個端點;二是把其中的兩條線段看成是兩個對應三點形的兩條對應邊(它們的交點應在第三條線上),剩余一條線段的兩個端點分別看成是兩個對應三點形的另外兩對對應邊的交點。顯然,前者用德薩格定理的逆定理,后者用德薩格定理。
2 應用德薩格定理的基本方法
在應用德薩格定理時,正確地選用適當的兩個對應三點形是解決問題之前提,這適當的兩個對應三點形往往需要通過分析并調整對應的頂點而得出。
例1 過三角形 的三個頂點任作共點的三條直線AE、BF、CG,分別與對邊交于E、F、G,若BC×FG=X,CA×GE=Y,AB×EF=Z,則X、Y、Z三點共線。
分析 如圖1:設AE、BF、CG共點O,要證X、Y、Z三點共線,就需將此三點看成兩個三點形之對應邊交點,且這兩個三點形對應頂點的連線須共點。按已知件BC×FG=X,CA×GE=Y,AB×EF=Z,且AE、BF、CG共點O,所以尋找的兩個三點形構想應是如圖2:
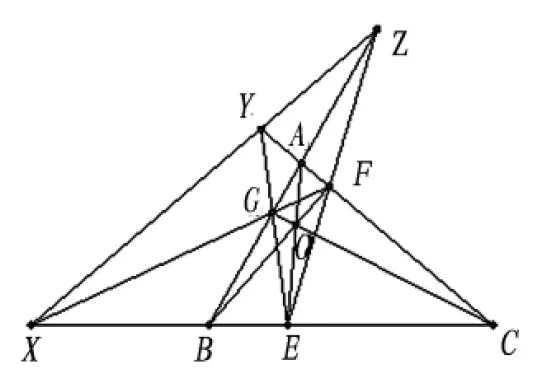
圖1 例1示意圖
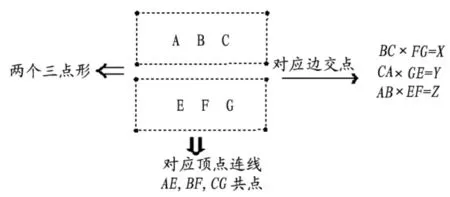
圖2 例1示意圖
證明 對于△ABC和△EFG:
∵ 它們三對對應頂點的連線AE、BF、CG共點O;
∴ 由德薩格定理,其三對對應邊的交點X、Y、Z三點共線。
應用德薩格定理時,關鍵是準確地找到兩個對應的三點形,而且要調整好兩個三點形之六點的對應頂點順序,以便達到證明的目的。
例2 設XYZ是完全四點形ABCD的對邊三點形,XZ分別交AC、BD于L、M,求證YZ、BL、CM共點。
分析 如圖3:要證明YZ、BL、CM共點,就需要把每條直線看成兩個點的連線,此六個點分成每三點一組構成兩個三點形,且這兩個三點形的對應邊的交點須共線。為此,通過調整對應的頂點,所以尋找的兩個三點形思路應是如圖4。
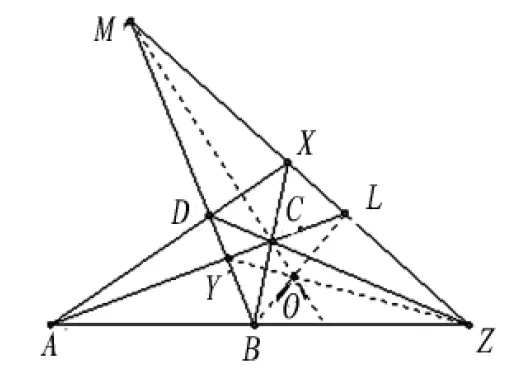
圖3 例2示意圖
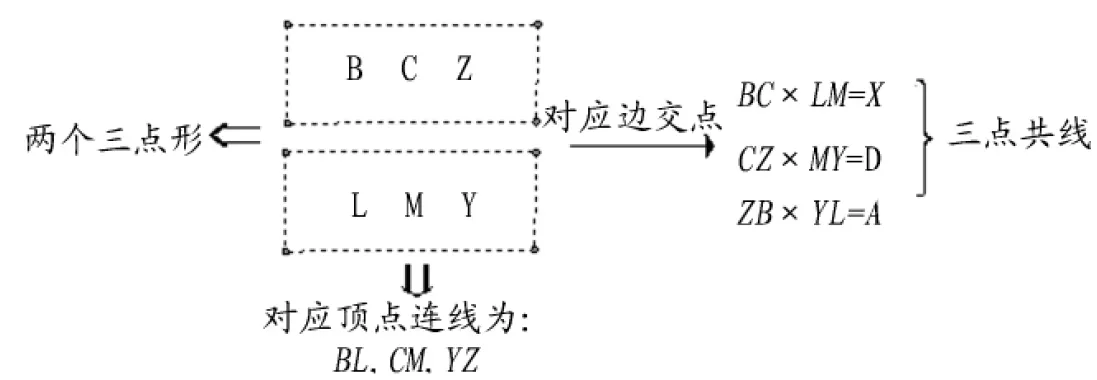
圖4 例2示意圖
證明 對于△BCZ和△LMY:
∵ 三對對應邊的交點BC×LM=X,CZ×MY=D,ZB×YL=A, 共完全四點形的AD邊;
∴由德薩格定理的逆定理,其三對對應頂點的連線YZ、BL、CM共點。
3 應用德薩格定理的靈活性
在應用德薩格定理解決問題時,兩個對應三點形的選擇不一定是唯一的。靈活地正確選用適當的兩個對應三點形顯得尤其重要。
例3 設ABCD是一個四面體,點X在BC上,一直線過X分別交AB,AC于P,Q,另一直線過X,分別交DB,DC于R,S求證:PR與QS的交點E在AD上。
分析1 如圖5:要證明PR與QS的交點E在AD上,即要證明PR、QS、AD共點E。
證法1 在△PQA和△RSD中,對應邊交點PQ×RS=X,QA×SD=C,AP×DR=B,
∵X、B、C共線,
∴由德薩格定理的逆定理得PR、QS、AD三直線共點E,所以,PR與QS的交點E在AD上。
分析2 如圖5:要證明PR與QS的交點E在AD上,即要證明A、D、E三點共線,
太谷縣沒有出臺飲用水水源地保護的相關辦法,僅由水庫編制了《龐莊水庫水源地保護管理辦法》報水務局,沒有形成正式條文。水源地保護未明確相關責任部門及責任人。水庫權限有限,對污染水源、破壞防護設施行為只能采取教育、勸戒手段,不能采取有效制裁措施,起不到威懾作用。未建立水源地安全保障部門聯動機制,不能實現信息互享,不能保障應急突發事件的及時處置和安全解決。
證法2 對于△BPR與△CQS,由于三對對應頂點連線BC,PQ,RS共點X,由德薩格定理可知,其對應邊交點BP×CQ=A,BR×CS=D,PR×QS=E共線,所以,PR與QS的交點E在AD上。
分析3 如圖5:要證明PR與QS的交點E在AD上,只需證明AE通過D即可。
證法3 對于△ABC與△ERS,對應邊交點AB×ER=P,BC×RS=X,AC×ES=Q,
∵X、P、Q共線,
∴ 由德薩格定理的逆定理得BR、CS、AE三直線共點,又BR、CS交于D,所以,AE通過D,即E在AD上。
例4 設OX,OY,OZ為三條定直線,A,B為兩定點,R為OZ上的動點,直線RA,RB分別與OX,OY交于P,Q,求證PQ經過AB上的一個定點。
分析 因為R是動點,作R的另一個位置R′,相應地得到P′,Q′,設P′Q′,PQ交于點C,只要證明A、B、C三點共線,本題得證;由OX,OY,OZ共點于O,只要找到一對對應的兩個三點形,其三對對應頂點分別在OX,OY,OZ上且三對對應邊交點恰為A、B、C三點即可。
4 應用推廣
定理1 如果兩個三點形對應頂點的連線都平行,則對應邊的交點在一直線上。
證明 ∵ 兩個三點形對應頂點的連線都平行,即這三連線共一無窮遠點,
∴由德薩格定理得兩個三點形對應邊的交點在一直線上。
定理2 如果兩個三點形三對對應邊分別平行,則對應頂點的連線交于一點。
證明 ∵ 兩個三點形對應邊分別平行,即兩個三點形每一對對邊的交點都是無窮遠點,
∴共無窮遠直線,
∴由德薩格定理的逆定理得對應頂點的連線交于一點。
例5 求證:△ABC的外心O、垂心E、重心D三點共線。
證明 如圖7:設F、G分別為BC、CA邊上的中點,連結OF、FG、GO、AE、EB, 在兩個三點形ABE與FGO中,三對對應邊
AE∥OF(平面內垂直于同一直線的兩直線平行)
BE∥OG(平面內垂直于同一直線的兩直線平行)
AB∥FG(三角形的中位線平行于第三邊)
∴由定理2知:兩個三點形的對應頂點連線AF、BG、EO共點。
∴D=AF×BG與E、O三點共線。
總之,應用德薩格(Desargues)定理或逆定理去解決一些“點共線”和“線共點”問題時,不單需要綜合分析已知條件和所證結論等因素,還需要熟練地掌握選擇兩個恰當的三點形這一關鍵的基本方法和思想,這樣,問題解決起來就非常簡捷、方便、靈活。在應用方面,德薩格定理的逆定理與德薩格定理具同樣的應用方法和價值。德薩格定理蘊含豐富的數學思想方法,對具體問題的處理方法具有獨特性,是證明“點共線”和“線共點”問題實用性很強的理論工具。
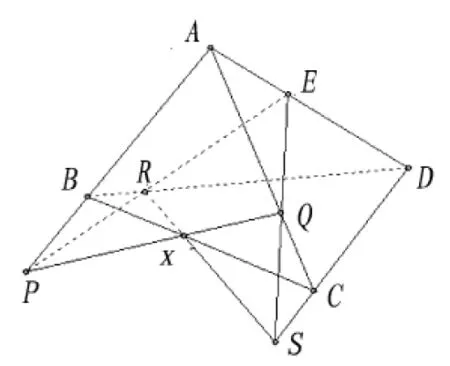
圖5 例3示意圖
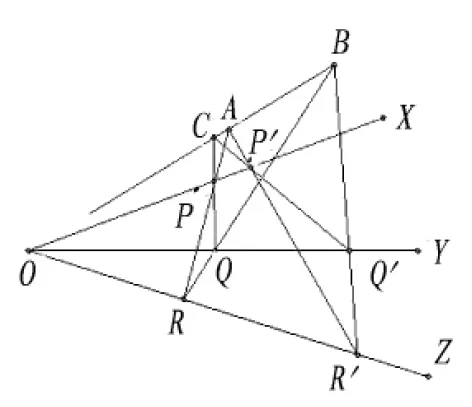
圖6 例4示意圖
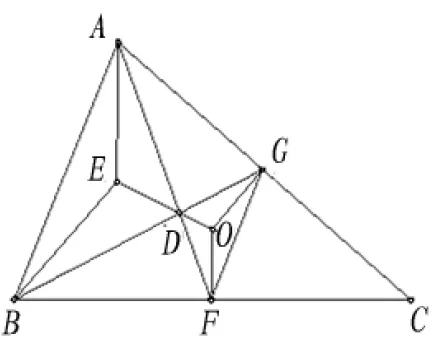
圖7 例5示意圖
[1]梅向明,劉增賢.高等幾何[M].北京:高等教育出版社,2008.
[2]梅向明,劉增賢.高等幾何學習指導與習題選解[M].北京:高等教育出版社,2003.
[3]趙臨龍,郭玲玲.Desargues三角形定理及其逆定理的關系與應用[J]. 牡丹江師范學院學報(自然科學版),2012,(2):6~7.
Desarguestheoremandthecollinearpointsandlinesoftheconcurrentproblem
HUANG Zheng-hua
(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002,China)
Desargues theorem and its converse therom are practical theoretical tools to prove the collinear points and concurrent lines.this paper discuss the application of Desargues theorem and its converse therom in proving collinear points and concurrent lines problems.
desargues theorem;collinear points;concurrent lines;infinite element
2013—09—19
黃振華(1960— ),男,黃石人,副教授,從事幾何教學與研究.
O185.1
A
1009-2714(2014)01- 0111- 04
10.3969/j.issn.1009-2714.2014.01.024

