顧及系數矩陣常數列的總體最小二乘迭代解法

汪奇生，楊德宏

(昆明理工大學 國土資源工程學院, 云南 昆明 650093)

顧及系數矩陣常數列的總體最小二乘迭代解法

汪奇生，楊德宏

(昆明理工大學 國土資源工程學院, 云南 昆明 650093)

介紹總體最小二乘的奇異值分解法(SVD)和混合總體最小二乘法(LS -TLS)，基于間接平差原理推導一種總體最小二乘迭代解法，可以用來解決系數矩陣含常數列的總體最小二乘平差問題。最后分別對系數矩陣不含常數列和系數矩陣含常數列的算例進行驗證，得到的結果與采用奇異值分解法和混合總體最小二乘法計算的結果相同，表明算法的有效性。

總體最小二乘；間接平差；迭代解法；混合總體最小二乘；奇異值分解

在測量數據處理中，對于系數矩陣含有誤差的平差問題，采用總體最小二乘法[1]要比采用最小二乘法在理論上更加嚴密。近年來，總體最小二乘得到了測量學者們的廣泛關注，一些針對測量數據處理的迭代算法相繼被提出[2-6]。同時，總體最小二乘也被用來解決具體的測量問題[7-10]。但在實際的測量數據處理中，系數矩陣有可能不是所有元素都含有誤差，而一些常規(guī)的迭代算法與奇異值分解法(SVD)一樣都無法顧及系數矩陣的常數列，而是對系數矩陣所有元素都進行了改正，這是不合理的。因此，混合總體最小二乘法[7-9]被用來解決系數矩陣含常數列的總體最小二乘問題，但混合總體最小二乘解算較為復雜。鑒于此，本文基于間接平差原理推導了一種總體最小二乘迭代算法。該算法充分考慮了間接平差的優(yōu)點，推導過程簡單且能顧及系數矩陣中的常數列，使用方便。最后通過線性擬合和坐標轉換的算例驗證了算法的合理性和有效性。

1 奇異值分解法與混合總體最小二乘法

1.1 奇異值分解法(SVD)

總體最小二乘的平差模型為

(1)

式中，V,EA分別表示觀測向量L和系數矩陣A的誤差，根據總體最小二乘原理，對參數估計的準則為

VTV+vec(EA)Tvec(EA)=min.

(2)

式中，vec(·)表示矩陣的拉直運算。一般采用奇異值分解法[1-3]來求取參數的總體最小二乘解。將式(1)可變換為

(3)

(4)

其中：

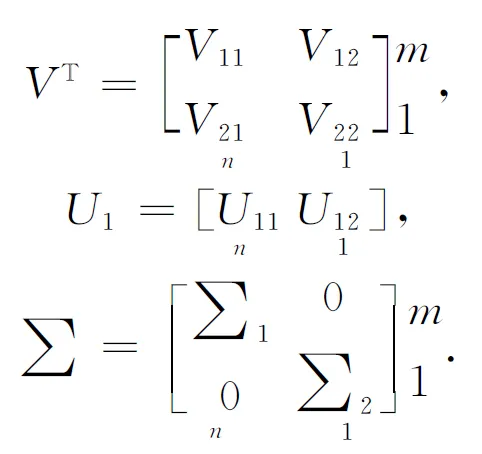
為求得參數的估值使式(2)達到最小，可將式(3)改為

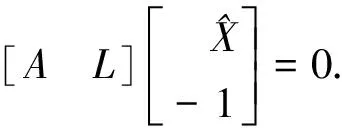
(5)

則可得參數的估值

(6)

其殘差矩陣為

(7)

進一步可計算單位權中誤差以及參數的協(xié)方差

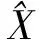
(8)

1.2 混合總體最小二乘法(LS -TLS)

(9)

式中:A1為系數矩陣的常數列，A2為除常數列后的數據列。混合總體最小二乘的約束條件為

(10)

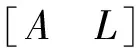
(11)

為求得參數的估值使式(10)達到最小，可將式(3)改為

(12)

由式(11)、式(12)即可得

R11X1+R12X2=R1L，

R22X2=R2L.

(13)

2 算法推導

將式(1)表示成V的函數為

L.

(14)

vec(ΔeA)=ΔvA.

(15)

式中,vec表示向量拉直運算，由文獻可知

vec(ABC)=(CT?A)vec(B).

(16)

化簡整理后可得

(17)

式中，?為矩陣的可內克積。根據總體最小二乘原理，求解的參數需要滿足如下極值條件：

VTV+(VA)TVA=min.

(18)

則可將式(17)寫成間接平差形式

(19)

根據間接平差原理，參數的求解為

(20)

單位權中誤差評定公式為

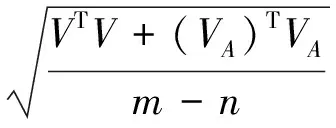
(21)

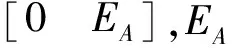
根據前述推導，總體最小二乘迭代解法的具體步驟如下：

1)按總體最小二乘原理計算參數的初值X0。

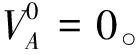
4)重復3)，直到兩次計算的參數之差小于給定的迭代限差，則停止迭代。

5)輸出參數值，計算單位權中誤差。

3 算例分析

3.1 線性擬合

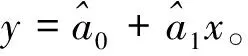
方案1：直接采用奇異值分解法求得的線性回歸方程為y=6.74-0.99x。

方案2：根據文獻[2]將數據中心化后，再采用奇異值分解法求得的線性回歸方程為y=6-x。

方案3：直接采用混合總體最小二乘法求得的線性回歸參數y=6-x。

方案4：直接采用本文推導的迭代算法求得的線性回歸方程為y=6-x。

從以上4種方案中可以看出，方案1直接采用奇異值分解法而沒有顧及系數矩陣常數列得到的結果不合理，方案2將數據中心化后，系數矩陣變?yōu)橐涣性厍也缓盗校俨捎闷娈愔捣纸夥ㄇ蟮玫慕Y果與方案3中直接采用混合總體最小二乘法求得的結果一致，是正確合理的。而方案4中直接采用本文的迭代算法求得的結果與方案2、方案3一致，故本文算法是合理有效的。

3.2 坐標轉換

為進一步驗證本文算法的正確性，選取文獻[11]例7～14的數據，用5個擁有WGS-84和北京54坐標的公共點來求取坐標轉換參數。根據坐標轉換的平差模型可知，其系數矩陣含有3列常數列，分別采用最小二乘法(LS)、混合總體最小二乘法(LS -TLS)、本文的總體最小二乘算法(TLS)來計算坐標轉換參數，計算結果如表1所示，單位權中誤差評定如表2所示。

表1 不同方法求得的坐標轉換參數

表2 不同方法的單位權中誤差評定結果 m

從表1的不同方法求得的坐標轉換參數計算結果可以看出，采用本文的迭代算法求得的轉換參數與采用混合總體最小二乘法求得的結果一致，這是因為本文算法可以顧及系數矩陣的常數列且對其不進行改正，而混合總體最小二乘法正是只改正系數矩陣含誤差的那部分。這也可以從單位權中誤差的評定結果中看出，采用本文的迭代算法計算的單位權中誤差與采用混合總體最小二乘法計算的結果一致，且小于采用最小二乘計算的結果。這也說明采用總體最小二乘求取坐標轉換參數要比采用最小二乘的精度高，故本文給出的算法較為合理。

4 結束語

基于間接平差原理，推導了一種總體最小二乘迭代算法。該算法推導過程簡捷易懂，迭代格式簡單且易于編程實現。同時，該算法可以顧及系數矩陣的常數列，這彌補了總體最小二乘的奇異值分解法和常規(guī)的總體最小二乘迭代算法的不足。通過最后的算例驗證了本文算法的合理性。

[1]GOLUB G H，VAN L C F. An Analysis of the Total Least Squares Problem[J].SIAM J Numer. Anal，1980，17:883-893．

[2]邱衛(wèi)寧，陶本藻，姚宜斌，等.測量數據處理理論與方法[M].武漢: 武漢大學出版社, 2008．

[3] 魯鐵定,周世健.總體最小二乘的迭代解法[J].武漢大學學報：信息科學版，2010,35(11) :1351-1354.

[4] 許超鈐，姚宜斌，張豹,等.基于整體最小二乘的參數估計新方法及精度評定[J].測繪通報，2011(10):1-4.

[5] 孔建，姚宜斌，吳寒．整體最小二乘的迭代解法[J]．武漢大學學報:信息科學版，2010，35(6):711-714．

[6] 邱衛(wèi)寧,齊公玉,田豐瑞. 整體最小二乘求解線性模型的改進算法[J].武漢大學學報：信息科學版，2010，35(6):708-710.

[7]張海華，劉春.顧及粗差的混合最小二乘平差實驗分析[J].現代測繪，2010，33(5):8-11.

[8]陳義，陸玨，鄭波．總體最小二乘方法在空間后方交會中的應用[J].武漢大學學報：信息科學版， 2008,33(12):1271-1274.

[9]陸玨，陳義，鄭波.總體最小二乘方法在三維坐標轉換中的應用[J].大地測量與地球動力學，2008,28(5):77-81.

[10]劉運明，鄒積亭，邊春雷.基于整體最小二乘的盾構環(huán)中心擬合方法[J].測繪通報，2010(Z):174-176.

[11]袁豹,岳東杰.關于總體最小二乘方法適應性實驗研究[J].測繪工程，2012，21(6):22-26.

[12] 武漢大學測量平差學科組編.誤差理論與測量平差基礎[M].武漢:武漢大學出版社,2003.

[責任編輯：劉文霞]

Iterative algorithm of total least squares considering the constant sequence of coefficient matrix

WANG Qi-sheng，YANG De-hong

(School of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093，China)

It briefly introduces a total least squares singular value decomposition (SVD) and mixed total least squares (LS-TLS). An iterative algorithm for total least squares is derived based on a principle of indirect adjustment, which can be used to solve the adjustment problems of total least squares for coefficient matrix containing constant sequence. Finally, numerical examples of the coefficient matrix with out constant sequence and with constant series are analyzed respectively. The results are the same used by the singular value decomposition method and the mixed total least squares and shows the effectiveness of the algorithm.

total least squares; indirect adjustment; iteration algorithm; mixed total least squares (LS-TLS); singular value decomposition (SVD)

2013-07-15

汪奇生(1989-)，男，碩士研究生.

P207

：A

：1006-7949(2014)07-0038-03