一種高效的最小獨立閉合環自動搜索算法

馬洪磊，劉成龍，余樂義，孟凡超

(西南交通大學 地球科學與環境工程學院，四川 成都 610031)

一種高效的最小獨立閉合環自動搜索算法

馬洪磊，劉成龍，余樂義，孟凡超

(西南交通大學 地球科學與環境工程學院，四川 成都 610031)

依據圖論理論，在基于生成樹、余樹變換的閉合環搜索算法和基于深度優先的閉合環搜索算法的基礎上，提出一種高效且穩定性好的控制網最小獨立閉合環自動搜索算法。

生成樹；余樹；深度優先；閉合環搜索

閉合環搜索及閉合差檢查是控制網外業測量數據處理過程中的重要環節，閉合環閉合差的大小是評判控制網外業觀測數據好壞的重要指標，此外，閉合差還可用于判斷外業測量數據中是否含有系統誤差或粗差。傳統的人工閉合環搜索方法雖然靈活，但當控制網極其復雜時，人工搜索法效率低，容易出錯，因此，尋找一種穩健、高效的閉合環自動搜索算法十分必要。目前，閉合環的自動搜索算法主要有3種：①基于鄰接矩陣變換的閉合環搜索法；②基于生成樹、余樹變換的閉合環搜索法；③基于深度優先搜索的閉合環搜索法。文獻[1]中對上述3種閉合環自動搜索算法進行了探討并得出以下結論：基于鄰接矩陣變換的閉合環搜索算法雖然簡單，但其時間和空間復雜性較高；基于生成樹、余樹變換閉合環搜索算法和基于深度優先的閉合環搜索算法的搜索效率相對較高[1]。文獻[2]中對基于生成樹、余樹變換的閉合環搜索算法和基于深度優先的閉合環搜索算法進行了理論分析并得出以下結論：基于生成樹、余樹變換的閉合環搜索算法能夠穩定地搜索出全部獨立閉合環，通過改變余枝的添加順序，可穩定地搜索出一組最小獨立閉合環。本文還通過一個實例證明了基于深度優先的閉合環搜索算法具有不穩定的缺點，具體是指：雖然該算法可以保證搜索出的閉合環之間相互獨立，但卻不一定能夠搜索出全部獨立閉合環[2]。雖然基于生成樹、余樹變換的閉合環搜索算法是一種穩定、可靠的閉合環自動搜索算法，但對大型控制網的最小獨立閉合環搜索效率不高[3]。針對以上各閉合環搜索算法中存在的不足，本文依據圖論中的相關理論并結合現有的基于生成樹、余樹變換的閉合環搜索算法和基于深度優先的閉合環搜索算法，提出了一種新的閉合環自動搜索算法，為論述方便，本文將該算法簡稱為新算法。

1 相關概念

生成樹：在一個連通圖G(V,E)中，其中V是圖中頂點的集合，E是圖中邊的集合。取它的全部頂點V和一部分邊E′構成一個子圖g(V,E′)，若子圖g(V,E′)中的邊將圖G(V,E)中的所有頂點連通又不形成回路，則稱子圖g(V,E′)是連通圖G(V,E)的一棵生成樹[4]。

廣度優先生成樹：由廣度優先搜索得到的生成樹為廣度優先生成樹[4]。

余樹：得到連通圖G(V,E)的生成樹g(V,E′)后，連通圖G(V,E)中不在生成樹上的邊稱為圖G(V,E)的余枝，余枝的集合稱為圖G(V,E)的余樹[5]。

深度優先搜索算法：是指沿著一條路徑從開始頂點到達最后的頂點，然后原路返回，并且沿下一條路徑達到最后的頂點，如此繼續直到走過所有的頂點[6]。

廣度優先搜索算法：又稱寬度優先搜索或橫向優先搜索，是指從根節點開始，沿著樹的寬度遍歷樹的節點[6]。

冗余搜索:也稱多余搜索即不必要的搜索。現有閉合環搜索算法中普遍存在大量的冗余搜索，嚴重影響了閉合環的搜索效率。

2 新算法原理與步驟

新算法結合了廣度優先和深度優先搜索原理，綜合了基于生成樹、余樹變換的閉合環搜索算法和基于深度優先的閉合環搜索算法的優點。其搜索過程可分為兩個階段：①獲得一棵廣度優先生成樹所對應的余樹；②對余樹中的余枝進行閉合環搜索。階段1所得余樹屬于一組獨立閉合環，階段2通過控制余枝的搜索過程，確保得到一組最小獨立閉合環。

利用新算法進行最小獨立閉合環搜索的具體步驟如下：

1)構建一維數組V和鄰接矩陣M分別用來存儲圖中所有頂點及點間關系(邊)的數據。考慮到鄰接矩陣對稱的特點，可采用下三角方式存儲。

2)利用廣度優先搜索算法獲得一棵廣度優先生成樹所對應的余樹。

3)設置當前搜索深度MD=2。

4)斷開余枝R，利用深度優先搜索原理對余枝R兩頂點進行最短路徑搜索(為便于論述，下文稱為對余枝進行閉合環搜索)，若搜索出的閉合環中不包含其他余枝，則記錄該閉合環并從余樹中刪除余枝R(即R不再為余枝)，重復步驟3)和4)；若搜索出的閉合環中包含其他余枝，則斷開其他余枝，繼續在當前搜索深度MD下對該余枝進行閉合環搜索，直到搜索到的閉合環中不包含其他余枝或閉合環搜索失敗為止；若搜索到不包含其他余枝的閉合環，則恢復之前斷開的余枝并記錄該閉合環，從余樹中刪除余枝R并重復步驟3)和4)；若搜索失敗，則恢復之前斷開的余枝并對下一條余枝重復步驟4)。

5)若余樹為空，則閉合環搜索完畢，否則執行步驟6)。

6)設置當前搜索深度MD=MD+1，重復步驟4)和5)。

3 新算法分析

上述新算法步驟簡單，只對余枝進行閉合環搜索，每搜索到一個閉合環就刪除一條余枝，余樹為空時閉合環搜索完畢，大大減少了冗余搜索且無需設置最大搜索深度。下面就新算法是否能穩定地搜索出一組最小獨立閉合環進行分析、論證。

3.1 穩定性和獨立性分析

穩定性是描述算法理論是否嚴密的方法。如果算法在任何情況下都能得到正確結果，則該算法是穩定的，否則該算法不穩定。

獨立性是指對于一組閉合環A，若A中任意閉合環中都至少有一條邊不存在于其他任何閉合環中，則認為該組閉合環是一組獨立閉合環。

由于新算法與基于生成樹、余樹變換的閉合環搜索算法都需要獲得余樹，但前者是在余樹范圍內，通過對鄰接矩陣進行深度優先搜索獲得閉合環，后者則是通過余枝回代至生成樹中獲得閉合環。基于生成樹、余樹的閉合環搜索算法余枝逐條回代保證了閉合環的獨立性，新方法要求每次搜索得到的閉合環中只含有一條余枝，也有效保證了閉合環的獨立性。又因為余枝個數等于獨立閉合環個數，因此，兩種算法均可以穩定獲得全部獨立閉合環。

3.2 最小性分析

圖1為某水準網示意圖，圖中水準網的樹形表示如圖2所示。圖2中實線集合表示廣度優先生成樹，虛線集合表示余樹，二者的組合為圖1所示水準網的另一種表示形式。對圖2分析不難發現，當每個閉合環的搜索都從搜索深度MD=2時開始，且滿足只含一條余枝的閉合環為搜索結果時，便可保證所得閉合環是一組最小獨立閉合環。為驗證以上分析的正確性，利用新算法對圖1所示水準網進行閉合環搜索，過程如下：

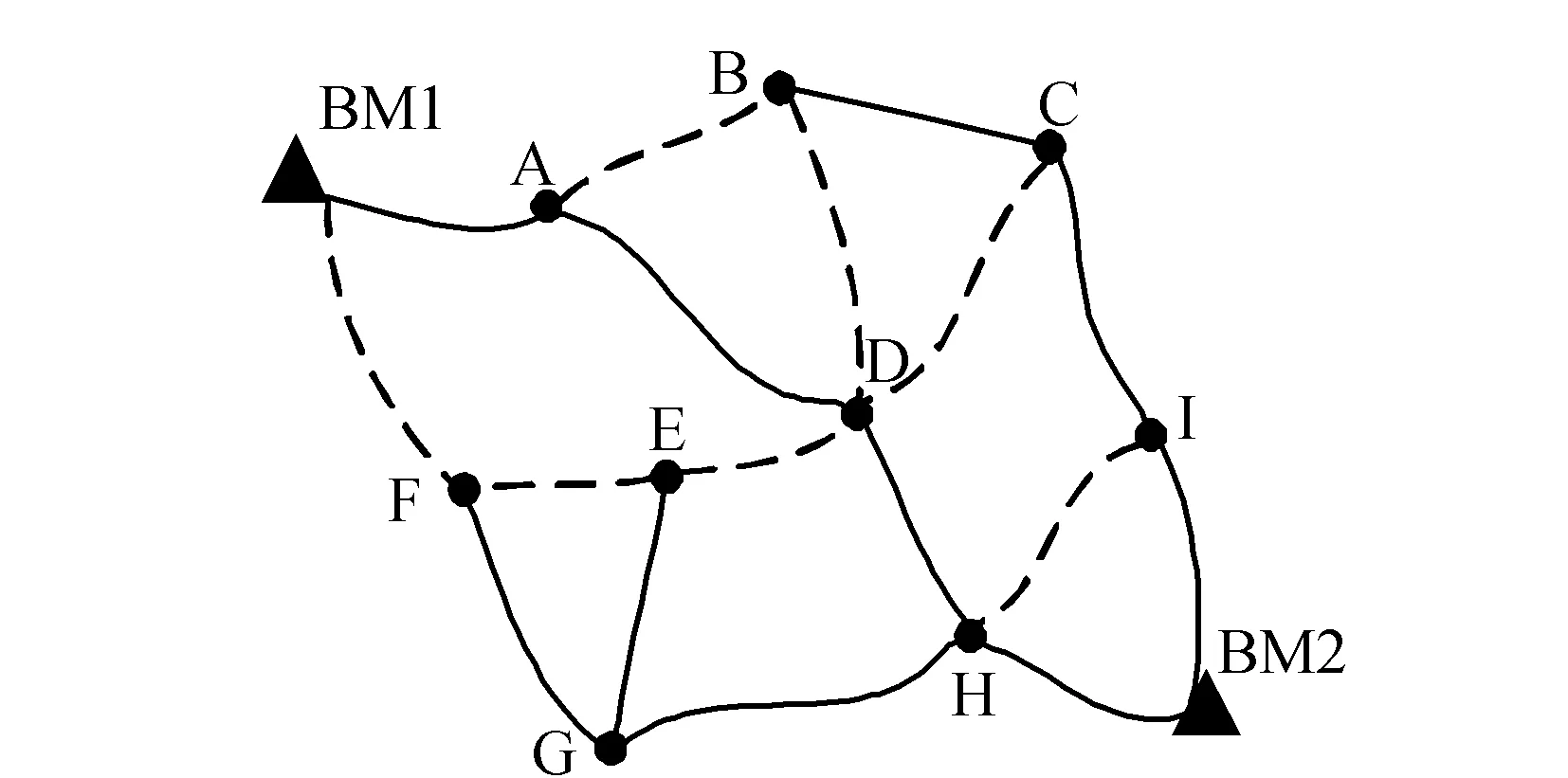
圖1 某水準網示意圖

圖2 圖1所示水準網的樹形表示

根據廣度優先搜索原理獲得該水準網圖的一棵廣度優先生成樹及相應余樹。依據新算法實施步驟可知，前兩個搜到的閉合環為I-H-BM2和E-F-G或E-F-G和I-H-BM2，第3個搜索到的閉合環為I-H-D-C或D-E-G-H，若第3個搜索到的閉合環為I-H-D-C，則第4個搜索到的閉合環為B-D-C,第5個搜索到的閉合環為A-B-D，第6個搜索到的閉合環為D-E-G-H，第7個搜索到的閉合環為A-D-E-F-BM1，至此閉合環搜索完畢，所得閉合環為一組最小獨立閉合環。若第3個搜索到的閉合環為D-E-G-H，則第4個搜索到的閉合環為I-H-D-C，第5個搜索到的閉合環為B-C-D，第6個搜索到的閉合環為A-B-D，第7個搜索到的閉合環為A-D-E-F-BM1，至此閉合環搜索完畢，所得閉合環為一組最小獨立閉合環。通過該實例，驗證了利用新算法進行最小獨立閉合環搜索的正確性。

對圖2進行分析發現，新算法在編程實現時還可進一步優化，優化方法如下：

在利用廣度優先搜索算法生成一棵廣度優先生成樹時，記錄每個頂點所在的層數(如圖2中BM2為0層，H和I為1層等)。得到廣度優先生成樹后，依據余枝中兩頂點所在層數之和的大小對余枝集合進行升序排列。此時，通過調整新算法步驟，可進一步減少冗余搜索。假設余樹中共有3條余枝且升序排序后順序為R1，R2，R3，則調整后步驟如下：

設置搜索深度MD=2，對R1進行閉合環搜索，若成功，則重置MD=2，并對下一條余枝R2進行搜索；若失敗，則設MD=MD+1，繼續對R1進行閉合環搜索。重復以上過程，當R3搜索成功時(即最后一條余枝搜索成功時)，閉合環搜索完畢。

4 對比分析

根據本文提出的新算法，筆者用C#語言在.Net平臺上編程實現了水準網最小獨立閉合環的自動搜索及閉合差的計算與檢核。為檢驗新算法是否具有較高的搜索效率，筆者還根據基于深度優先的閉合環搜索算法，同樣編程實現了水準網最小獨立閉合環的自動搜索。為節省存儲空間，筆者所編程序中的鄰接矩陣均采用下三角方式存儲，從而導致搜索時間延長，但這并不影響對新算法搜索效率的對比。自編程序與武漢大學商用平差計算軟件COSA及西南交通大學商用軌道控制網數據處理軟件CPⅢ DMS進行對比的情況，統計在表1～3中。

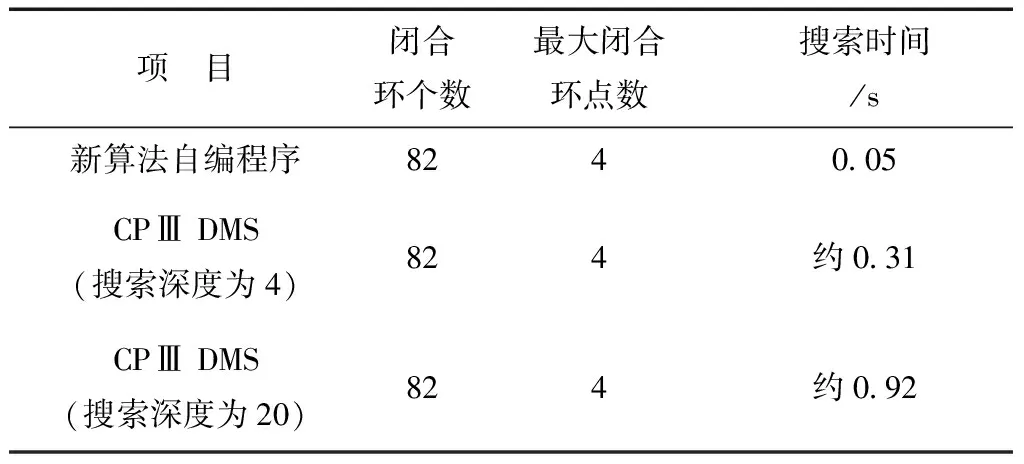
表1 CPⅢ高程網的最小獨立閉合環搜索結果對比

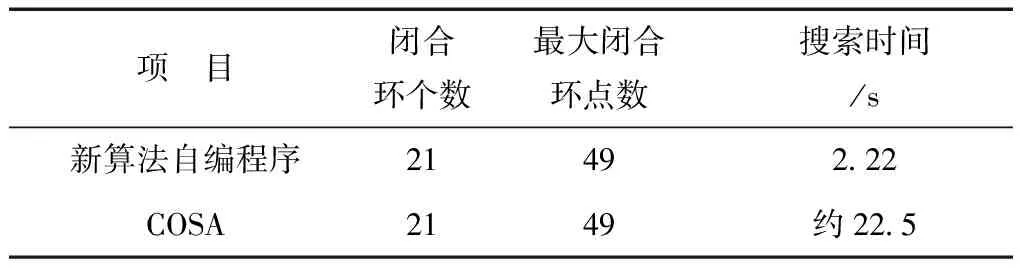
表2 某水準網的最小獨立閉合環搜索結果對比

表3 某水準網的搜索效率對比

以上各表中的統計數據均是在同一臺計算機上得到，表3中基于深度優先的閉合環搜索算法是在最大搜索深度為50的情況下得到的。

由表1、表2中閉合環個數及最大閉合環點數的對比可知，本文提出的新算法可準確地搜索出任意水準網的一組最小獨立閉合環，驗證了新算法的正確性及可行性。

文獻[2]中通過3種不同算法搜索時間的對比，發現基于深度優先的閉合環搜索算法是一種較快的閉合環搜索算法。由表3中搜索時間的對比可知，本文所提出的新算法較基于深度優先的閉合環搜索算法搜索時間更短、效率更高。

5 結 論

本文提出的新算法綜合了基于深度優先閉合環搜索算法和基于生成樹、余樹變換的閉合環搜索算法的優點，可理解為是對二者的融合和改進。通過以上理論分析及實例驗證得出以下幾點結論：

1)本文提出的閉合環自動搜索算法極大地減少了冗余搜索，顯著提高了閉合環的搜索效率，是一種適用于大型控制網的最小獨立閉合環自動搜索的新算法。

2)本文提出閉合環自動搜索算法雖然也利用了深度優先搜索原理，但改善了基于深度優先的閉合環搜索算法不穩定的缺點且無需設置最大搜索深度，是一種穩定、高效且高度自動化的最小獨立閉合環搜索算法。

3)本文提出的最小獨立閉合環自動搜索算法不僅能應用于高程網，原則上也適用于任何可化簡為無向圖的控制網的最小獨立閉合環的自動搜索，如GPS基線網及化簡后的邊角網等。

[1]趙一晗，伍吉倉.控制網閉合環搜索算法的探討[J].鐵道勘察，2006(3)：12-14.

[2]鄒進貴，馮晨.控制網最小獨立閉合環搜索算法研究[J].地理空間信息，2008，6(6)：97-99.

[3]游為，范東明，張云，等.水準網閉合差自動解算的新方法[J].測繪工程，2007，16(5)：17-19.

[4]嚴蔚敏，吳偉民.數據結構[M]. C語言版.北京：清華大學出版社，2007：156-191.

[5]馮琰，張正祿，羅年學.最小獨立閉合環與附合導線的自動生成算法[J].武漢測繪科技大學學報，1998，23(3)：255-258.

[6]楊洪.圖論常用算法選編 [M].北京：鐵道出版社，1988：110-121.

[責任編輯：劉文霞]

An efficient algorithm of automatic searching for minimum independent closed-loop

MA Hong-lei，LIU Cheng-long，YU Le-yi，MENG Fan-chao

(Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University， Chengdu 610031, China)

It provides an efficient and stable automatically search algorithm of smallest independent closed loop control network, according to the closed loop search algorithm of spanning tree and spare tree transform, and depth-first closed loop search algorithm on the basis of graph theory.

spanning tree; spare tree; depth-first; closed loop search

2013-08-14

中央高校基本科研業務專項資金資助項目(SWJTU12ZT07)

馬洪磊(1989-)，男，碩士研究生.

P221

：A

：1006-7949(2014)08-0070-03