時間序列分析在地鐵沉降監測中的應用

張 松，田林亞

(河海大學 地球科學與工程學院，江蘇 南京 210000)

時間序列分析在地鐵沉降監測中的應用

張 松，田林亞

(河海大學 地球科學與工程學院，江蘇 南京 210000)

采用時間序列分析的方法，通過對已獲取的地鐵沉降監測數據進行分析、建模，得到合理的沉降預測模型，不僅可以預測出短時間內地鐵區段的沉降量，并可了解地鐵區段短時間內的沉降趨勢。實驗證明，方法簡單、快速、準確，具有良好的短期預報效果。

地鐵；沉降監測；時間序列；數據處理；短期沉降預測

城市高層和地下建筑工程的施工過程中，通常都要開展沉降監測工作，掌握建筑物自身及其周邊其它建筑物的沉降量和沉降速率，對沉降狀況進行分析和評價，采用合理的數學模型和方法進行沉降預測，掌握沉降的發展趨勢和變化規律。

目前，對于沉降監測成果的應用主要有以下幾個方面：①掌握建筑物的沉降狀態，調整施工進度或加強安全防范措施；②驗證有關設計參數；③對數據進一步分析利用，對建筑物的沉降趨勢進行預測[1-2]。建筑物沉降監測成果是按照時間順序(或一定的空間順序)相繼發生的一組數據序列，具有3個特點:與時間相關，但不一定是時間的嚴格函數；帶有一定的隨機性，但彼此之間又具有一定的統計關系和統計規律；歷史數據的相關性隨著時間間隔的增大而減小。本文根據時間序列分析的基本方法，針對某城市地鐵保護區的沉降監測數據，建立沉降預測時間序列模型，通過沉降預測掌握地鐵結構短期的沉降發展趨勢。

1 沉降時間序列建模與預測

1.1 時間序列的平穩性檢驗

沉降時間序列分為平穩時間序列和非平穩時間序列兩類。平穩時間序列模型包括AR模型、MA模型、ARMA模型3類[3]，非平穩時間序列模型包括ARIMA模型和SARIMA季節模型。要建立合理的沉降時間序列模型，首先要對已有沉降時間序列的平穩性進行檢驗，這可以通過計算樣本數據的自相關系數來檢驗其平穩性，計算公式為

(1)

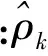
1.2 模型選擇與定階

如果沉降樣本序列經檢驗為平穩序列，可進一步根據樣本的自相關函數和偏自相關函數[4]進行模型的選擇和定階。若樣本的自相關函數呈現拖尾狀態，而偏自相關函數是p階結尾，則選擇AR(p)模型。

xt=φ0+φ1xt-1+φ2xt-2+…+φpx1+εt.

(2)

式中：xt為t時刻的觀測值；εt為該模型的白噪聲擾動項；φi(i=1, 2,…，p)為模型系數。

若樣本的自相關系數q階截尾，而偏自相關系數拖尾，則選擇MA(q)模型。

xt=θ0εt-θtεt-1-θ2εt-2-…-θqεt-q.

(3)

當樣本的自相關系數和偏自相關系數都拖尾時，則選擇ARMA(p,q)模型。

xt=μ+φ1xt-1+…+φpxt-p+

εt-θ1εt-1-…-θqεt-q.

(4)

根據自相關和偏自相關系數進行模型的選擇和定階存在一定的主觀性，通常情況下按照最小信息量準則AIC和SBC方法來選擇最優模型,AIC和SBC的值越小，表明模型越精確。

AIC=Tln(RSS)+2n.

(5)

SBC=Tln(RSS)+nln(T).

(6)

式中:n為待估參數個數(p+q+可能存在的常數項)；T為可使用的觀測值；RSS為殘差平方和。

1.3 模型的參數估計與檢驗

時間序列模型的類型和階數確定后，還要對模型參數進行估計，方法有矩估計、最小二乘估計和極大似然估計等[5]。模型檢驗是通過對提取信息后的殘差序列進行檢驗，若擬合后模型的殘差序列為不存在相關性的白噪聲序列，則表明該擬合模型是最優的，拉格朗日乘數(LM)檢驗是檢驗殘差序列是否存在高階相關性的一種有效方法[6]。

如果誤差項ut是p階序列相關的，則ut=λ1ut-1+λ2ut-2+…+λput-p+εt。若要證明ut是任意階不相關，則提出約束條件H0：λ1=λ2=…=λp=0。如果約束條件成立，LM服從χ2(p)分布。

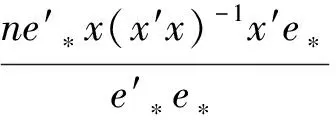
(7)

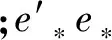
1.4 模型的預測

根據沉降觀測樣本序列{xk}建立的模型可以預測未來沉降xk+1…xk+m，當m=1時，稱作一步預測，當m>1時，為多步預測[7]。ARMA模型的預測公式為

(8)

當系數θi(i=1,2，…，p)的值為0時，即為MA(q)的預測公式。

2 實例應用與分析

2.1 工程概況

表1為某城市地鐵沉降監測數據，該地鐵已經處于運行階段，由于其附近建筑基坑的開挖，要求采用二等水準測量方法進行區段沉降監測，基坑的位置和監測點的布置如圖1所示。

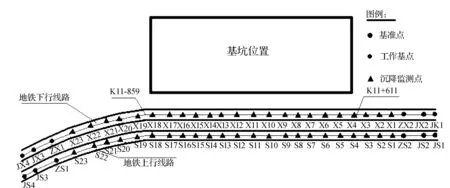
圖1 沉降監測點布置圖

本文采用靠近基坑中心的X11點的前14期沉降觀測值作為樣本數據，建模預測第15～20期的沉降量。

2.2 平穩性檢驗

前14期樣本數據的自相關系數值如表2所示，當k增大時，自相關系數迅速趨于0，并在0值附近波動，表明該序列為平穩的時間序列。

表1 沉降觀測值 m

表2 樣本數據自相關系數值

2.3 模型的選擇和求解

計算樣本的偏自相關系數，和自相關系數一同繪于圖2。由圖2可以看出，樣本數據的自相關系數在延遲3階后，迅速趨于0，并在0附近波動，可認為三階截尾。樣本的偏自相關系數在0值附近一直有較大的波動，呈現拖尾狀態。所以初步選定模型為MA(2)、MA(3)、MA(4)。

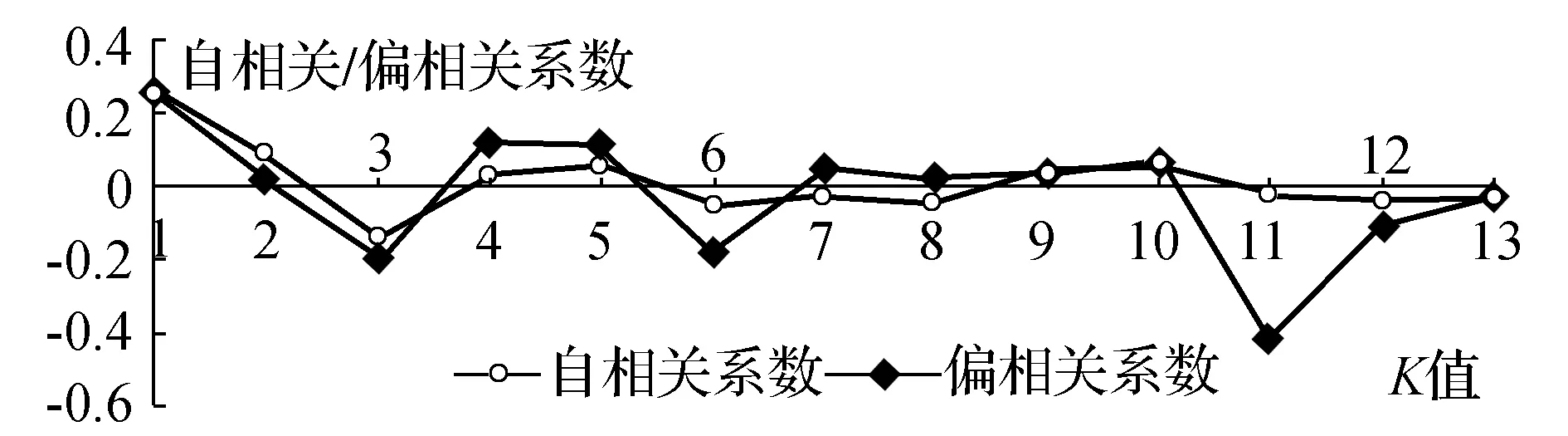
圖2 自相關與偏自相關系數對比

根據AIC、SBC方法進行模型檢驗，結果如表3所示，其中MA(3)模型的AIC、SBC值最小，因此選擇MA(3)模型。

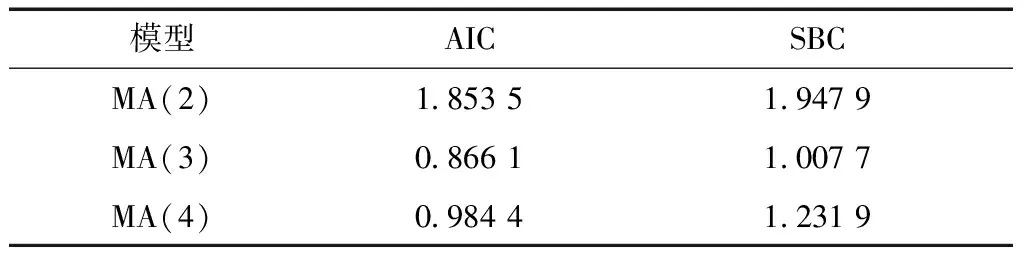
表3 模型最優檢驗表

根據最小二乘估計法求得模型系數，得到MA(3)模型為

xt=-1.8553+0.06589εt-0.151470εt-1-

0.906 946εt-2.

(9)

2.4 模型參數檢驗與預測

根據求得的模型對X11點的第15～20期的沉降量進行預測，預測方法包括1步循環預測、2步預測和3步預測，預測值及其與實測值的殘差如表4所示。

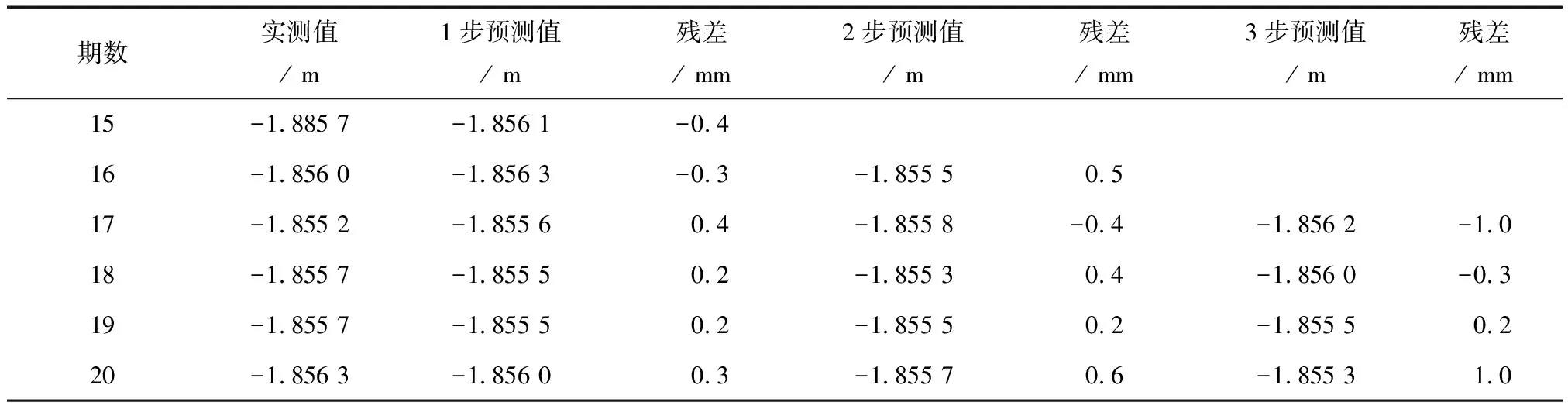
表4 預測值及其與實測值的殘差

根據表3可以得出如下結論：1步預測法精度最高，3步預測法精度最低；隨著步數的增加，殘差變大，并且預測值在常系數值附近波動(本例模型常系數值為-1.8553)，可見時間序列的短期預測效果較好；3步以內的沉降預測都具有良好的效果。

3 結束語

本文研究了時間序列分析方法在建筑物沉降監測中的應用。結合地鐵保護區沉降監測數據，采用時間序列分析的方法，通過對沉降量的計算與分析，得出該地鐵區段的沉降量為平穩時間序列，并進一步進行建模和預測，獲得較高的預測精度和較好的預測效果，說明利用時間序列模型進行沉降預測是完全可行和有效的，所建沉降預測模型能很好地反映地鐵區段的沉降變化規律。除此之外，沉降監測中還密切注意基坑附近的水位變化[8-9]、地鐵上方的材料堆積和地鐵內部的滲漏裂縫等，為掌握地鐵區段的沉降狀態和地鐵安全運營起到保障作用。

[1]黃聲享.變形監測數據處理[M].武漢：武漢大學出版社, 2003.

[2]蘭孝奇.建筑物沉降的時間序列分析與預報[J]. 河海大學學報, 2006,34(4):426-429.

[3]朱睿, 張俊中, 龍洋. 時間序列模型在建筑物沉降監測中的應用[J]. 測繪與空間地理信息, 2012, 35(2):213-216.

[4]石玉峰，孫保奇.時間序列分析及其在變形數據分析中的應用[J].金屬礦山, 2004(2):13-14.

[5]劉華夏.基于時間序列分析的地鐵變形監測數據建模與預報研究[J].鐵道勘察, 2009,17(3):17-19.

[6]錢爭鳴.非線性時序模型LM檢驗的兩類臨界值檢驗統計功效對比[J]. 數量經濟技術經濟研究, 2006(1):99-105.

[7]石雙忠.時序分析在變形監測數據處理中的應用[J].工程勘察,2004,32(3):59-67.

[8]鄭立常, 衛建東，鄭俊鋒，等. 基坑施工對鄰近運營地鐵隧道影響監測的實踐[J]. 測繪工程, 2007,16(2):47-49.

[9]周小莉，俞葒.信息化測繪條件下的地鐵施工監測方法探討[J].測繪工程，2014，23(9)：35-39.

[責任編輯：張德福]

Application of time series analysis to metro subsidence monitoring

ZHANG Song, TIAN Lin-ya

(School of Earth Sciences and Engineering,Hohai University, Nanjing 210000, China)

The time series analysis method is used to analysis the metro-subsidence monitoring data and to establish a reasonable model. Not only can the value of the subsidence monitoring be forcast, but also can grasp the subsidence trends of the metro in short time. Experiments prove that the method is simple, rapid, precise and has a good short-term forecasting results.

metro;subsidence monitoring; times series; data processing; short-term subsidence prediction

2013-08-25，2014-09-28補充更新

張 松(1989-)，男，碩士研究生.

TU196

：A

：1006-7949(2014)10-0063-04