沉降槽中射流管的理論及正交試驗研究

萬小立

（江西科技學院 機械工程學院，江西 南昌 330098）

沉降槽中射流管的理論及正交試驗研究

萬小立

（江西科技學院 機械工程學院，江西 南昌 330098）

本文探討了影響射流管效率的相關參數，確定了面積比為最主要的參數，提出了設計射流管最優參數的方法，通過正交試驗，驗證了該方法的有效性。

沉降槽；射流管；面積比；正交試驗

0 引言

沉降槽是氧化鋁生產過程中尤為重要的設備，用于溶出液的固液分離；沉降槽的產能（單位時間進料量）很大程度上決定了氧化鋁的產能。目前，沉降槽產能過低已經成為制約氧化鋁產能進一步擴大的一個瓶頸。國外很多學者對沉降槽進行了研究.其中，J.B.Farrow[1]等人對沉降槽中絮凝劑的絮凝效果進行了詳細分析；R.B.White[2]對沉降槽給料筒內的流場進行了可視化研究，優化了給料筒結構；M.R.udman、K.simic[3]和I.D.Sutalo[4]等人分別針對沉降槽內耙的結構設計進行了模型實驗研究。所有這些研究成果都能在一定程度上改善沉降槽工作性能，但效果不是很顯著。基于此，本文對本論文對沉降槽中射流管的參數進行了正交試驗研究。

1 射流管理論

改造沉降槽進料管，采用射流管的形式，使進料礦漿在射流管中，能通過射流管的吸附作用而卷吸沉降槽上層清液，進而達到稀釋的目的，即沉降槽進料內循環自稀釋技術。經過稀釋的進料礦漿，其固含降低，從而能提高赤泥沉降速度，使沉降槽產能和產品質量大幅度提高。實踐證明，利用射流管，使沉降槽進料進行內循環自稀釋，能使沉降槽產能、產品質量等都有大幅度的提升。

沉降槽中射流管的結構如圖1所示。其中，工作液為進料礦漿，被吸液為沉降槽清液，混合液為稀釋后的礦漿。沉降槽工作時，進料礦在噴嘴處由于過流面積急劇下降，礦漿流速急劇增大，從而卷吸周圍的沉降槽清液，兩種液體在喉管中充分混合后變成稀釋液后進入給料筒。

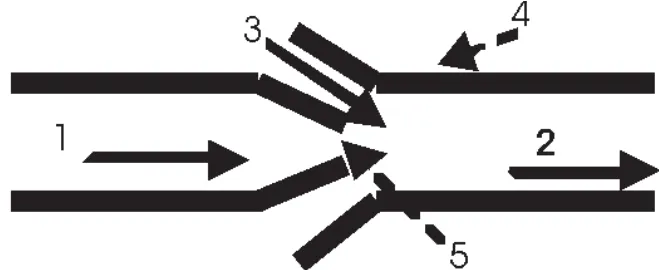
1-工作流體；2-稀釋流體；3-被吸流體；4-喉管；5-噴嘴

1.1 基本特征方程

影響射流管工作性能的幾個主要參數包括：面積比m、流量比q、壓力比p和密度比y。其中，面積比為噴嘴和喉管的過流面積比；流量比、壓力比和密度比分別為被吸液和工作液的體積流量比、壓力比和密度比。反應射流管這幾個主要參數之間相互關系的方程式就是射流管的基本特征方程[5]。

射流泵工作能量來源包括工作液提供能量Ea；射流泵工作能量輸出包括被吸液得到的能量Eb、工作液與被吸收液的混合損失能量Q、工作液通過噴嘴的能量損失Qa、被吸液通過吸入管道能量損失Qb、混合液在喉管中的能量損失Qc。由能量守恒可得：

單位時間內工作液提供的能量和被吸液得到的能量分別為：

工作液與被吸液的混合損失能量可以分為工作液從v1到v2減少的動能和被吸液從v3到v2增加的動能兩部分，兩者之差即為混合損失能量：

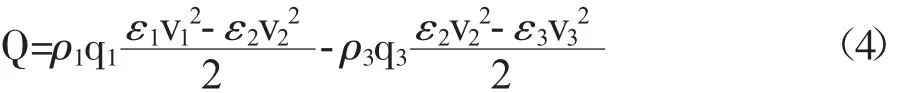
其中，ε1、ε2、ε3分別為進口管、吸入管、喉管中流體的動能修正系數。

射流泵內各個結構處的摩擦能量損失分別為：

其中，K1、K3、K2分別為流體在噴嘴、吸入管道以及喉管的摩擦損失系數。

綜合上述各式，可以得出：

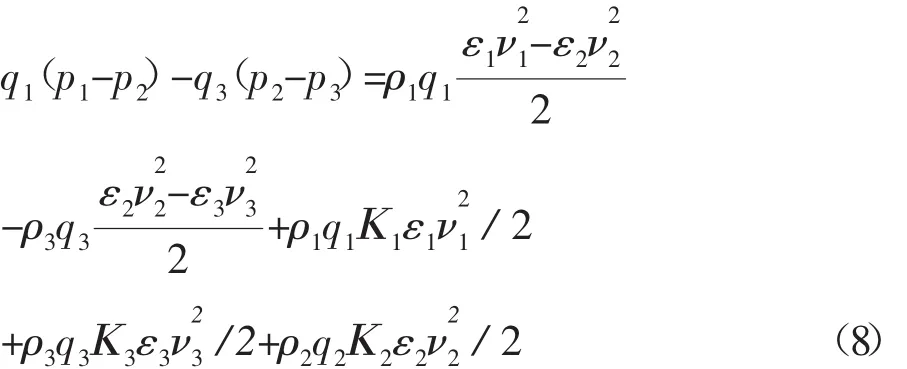
根據射流管的本身結構以及面積比m、密度比y和流量比q的定義，可以得出關系式：

對方程式（8）兩邊同時除以 ρ1p1，并根據式（11）以及流體連續性方程可得：

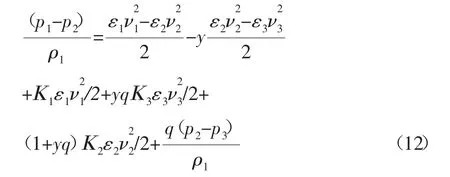
考慮到射流管中的壓力變化(如圖2所示),分別對工作液從p1到pe段、被吸液從p2到pe段應用伯努利方程可得：

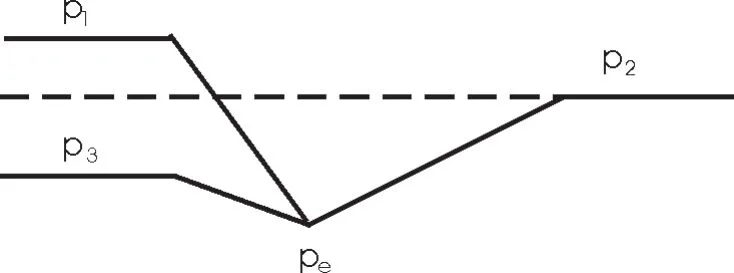
圖2 射流管中壓力變化趨勢

將式（13）和式（14）兩式相減，并根據式（9）到式（11），整理可得：

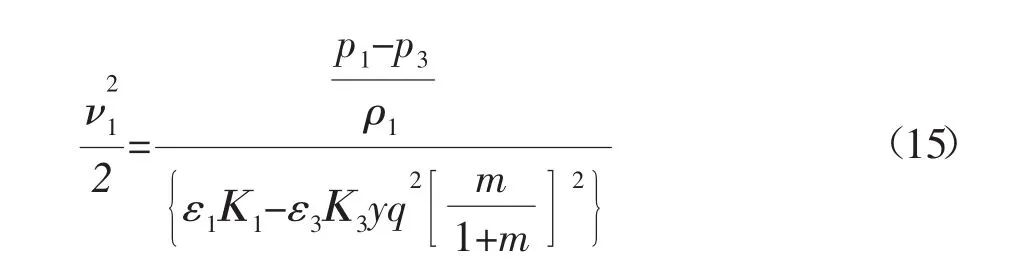
聯立式（12）、（15），整理后可得射流泵的特性方程為：

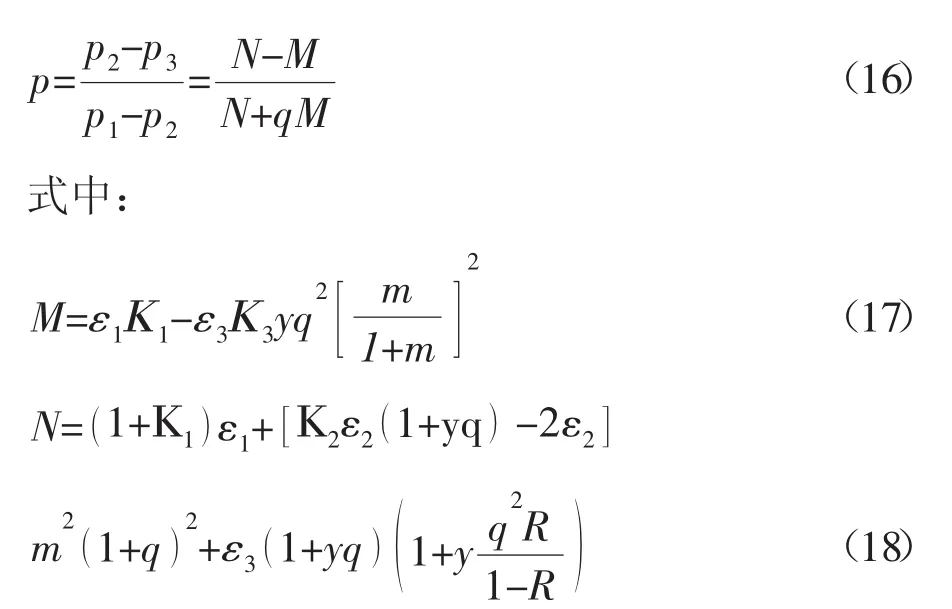
式（18）即為射流管的基本特征方程。

1.2 射流管的最優參數

根據射流泵效率的定義，有 E=q×p，將式（16）帶入（19），可得效率的相關表達式：

根據多元函數求極值的方法，式（19）對流量比q求偏導，可得出最佳流量比的表達式。

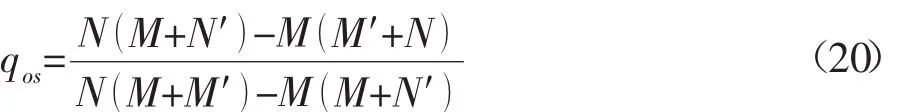
式（20）即為最佳流量比的隱函數表達式，可以根據迭代法求解。

摩擦損失系數及動能修正系數由射流管的材料、結構以及工質的性質決定。當工況的密度比確定時，最佳流量比就只與射流管的面積比m有關，即qos=f(m)，據此可以求出不同面積比情況下，射流管的最佳流量比，然后根據式（19）即可求出對應的最佳效率值。因此，只要確定射流管的面積比，就可以求出對應的最佳效率，最佳效率值和面積比之間有一一對應的函數關系。當面積比變動時，最佳效率也會隨之變化，顯然，在所有最佳效率之中還存在一個最大值，這個最大值就是射流管的最優效率，而與之對應的面積比即為射流管設計的最優面積比。由此可知，面積比是射流泵非常重要的一個設計參數[6]。

為了與實驗數據有可比性，這里設定動能修正系數為1，摩擦損失系數分別為 K1=0、K2=0.03、K3=0.28，密度比為1，采用Origin軟件進行計算，求出了最優流量比為1.02，對應的最優效率為34.65%，由此可計算出最優面積比為0.286。

2 正交試驗

2.1 實驗設計

按照正交試驗設計的一般步驟設計實驗。

試驗目的：探究不同面積比、喉嘴距和噴嘴角度對射流泵的影響；找出射流泵設計的最優參數。

試驗指標：測出不同流量比下進出口流量、壓力，以此計算效率作為試驗指標。

試驗因素：面積比m、噴嘴角度b、喉嘴距l。

制定因素水平表：實驗選取了三因素，分別有三個不同水平，制定的因素水平表如表1所示。其中，面積比的水平是根據Meakhail Tarek的正交試驗結果（0.25）[4]、Mallela R 的數值分析結果（0.28）[5]以及理論分析結果0.286來選取的，面積比三水平分別設置為 0.286、0.25、0.22。

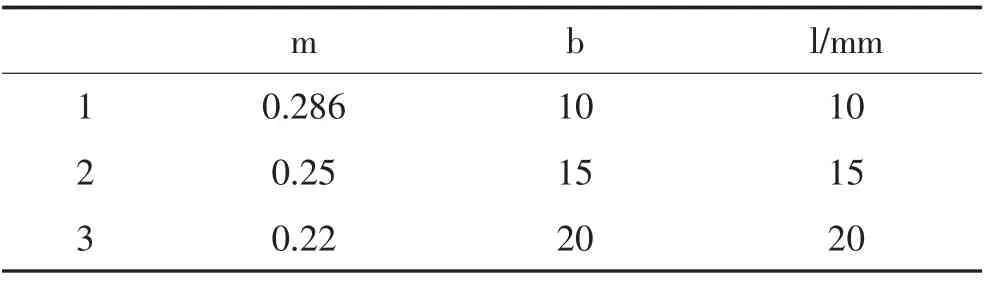
表1 因素水平表

選取正交表確定實驗方案：實驗中采用了三因素三水平，因此，要選用Ln(3m)型正交表。不考慮交互作用，有三個因數。因此，正交表選用L9(34)。正交表確定后，開始填表，按水平對號入座的方法填寫正交表，試驗方案如表2。

表2 L9(34)正交表

2.2 實驗過程

實驗中采用了9組不同噴嘴，對應9組實驗。整個喉嘴段可以根據實驗要求進行調節。測量儀器主要采用LZB轉子流量計、超聲波流量計和U型管壓力計。

本實驗采用LZB液體玻璃轉子流量計計量流量，具體型號和參數如下：LZB-25型，公稱通徑25mm，錐管長度350mm，工作壓力≤0.6MPa，精度等級 2.5，量程：100～1000l/h。LZB-25 型液體玻璃轉子流量計的基本測量范圍為20℃的水，可用于其它溫度其它液體的測量時，必須對讀數加以修正。讀數根據下式進行修正：

其中，QA表示轉子流量計讀數l/h，ρA表示20℃時水的密度，kg·m-3；ρ 表示實際被測液體密度密度，kg·m-3。

超聲波流量計采用TDS-100F1固定式超聲波流量計，配置標準S型傳感器。主要參數如下：測量精度：優于1%，重復性：優于0.2%；測量周期：500ms（每秒2次，每個周期采集128組數據）；工作電源：85～264VAC／24VDC 可選；流速范圍：0～±32m／s（流速分辨率0.001m／s）；標準S型傳感器適用管徑：DN15～DN100。

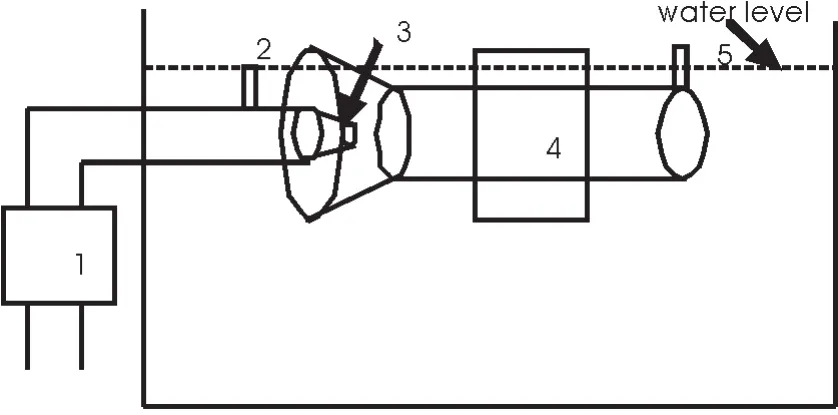
圖3 實驗裝置簡略圖

按照圖3搭建實驗臺。計算射流管中的摩擦損失系數分別為：K1=0、K2=0.03、K3=0.28，工作液和被吸液均采用水，密度比為1。

按照表2進行實驗。實驗中采用轉子流量計計量進口流量，采用U型管壓力計測壓力，超聲波流量計測喉管內的流量。實驗重復進行3次，取平均值進行計算。

實驗中記錄的一組實驗數據如表3。

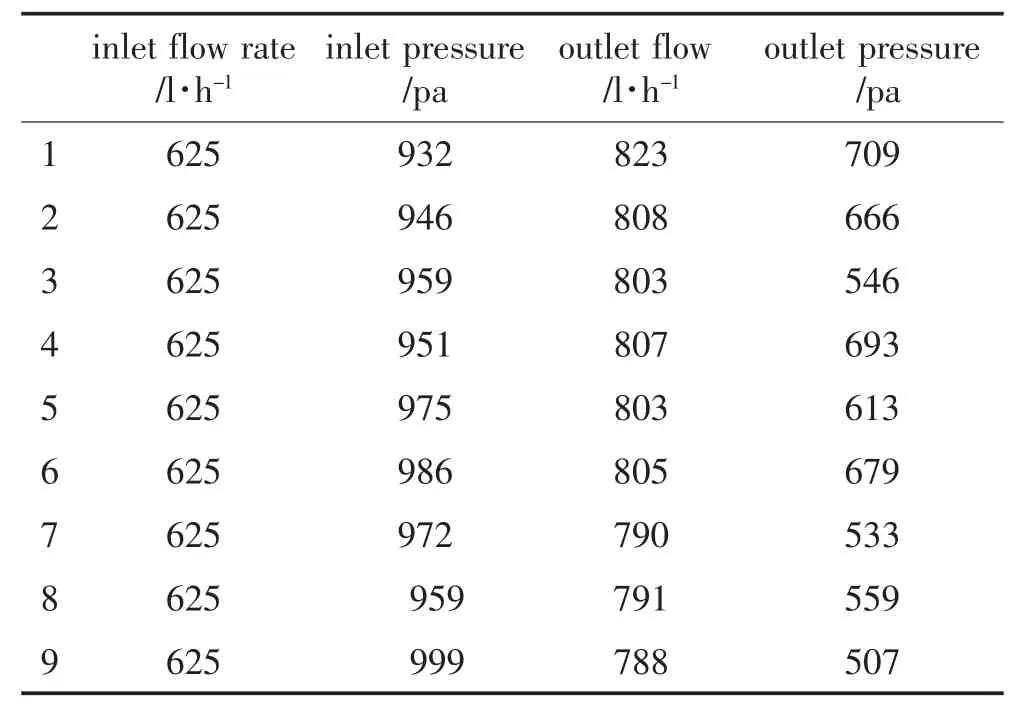
表3 實驗數據

3 試驗結果分析

3.1 極差分析

極差分析計算方法如下：

計算第j列上第i個水平的試驗結果總和為Kij。例如：

K11=24.17+20.63+16.29=61.09。

計算Kij的平均值K*ij=1/tKij，t為第j列上水平i出現的次數。例如：

K*11=61.09/3=20.36

稱 Rj=max｛Kij｝-min｛Kij｝為第 j列的極差。

所有計算結果見表4。分析可知K*11，K*21，K*31之間的差別僅僅是由A1，A2，A3引起的，而與B，C取什么水平無關。因此一般地可通過比較K*11，K*21，K*31的大小來確定m的最佳水平。而本實驗中因為K*11最大，說明m取m1水平最好。類似地，可確定b的最佳水平為b1，l的最佳水平為l1，由此得最優配置為m1b1l1。

根據極差可以判斷各個因素的主次順序。極差Rj越大說明該因素的水平變化對實驗指標的影響越大，即該因素越重要。因此根據實驗結果可以排出各因素的主次。由于 R1＞R3＞R2＞R4，因此 mbl三因素的主次順序為 m＞l＞b。

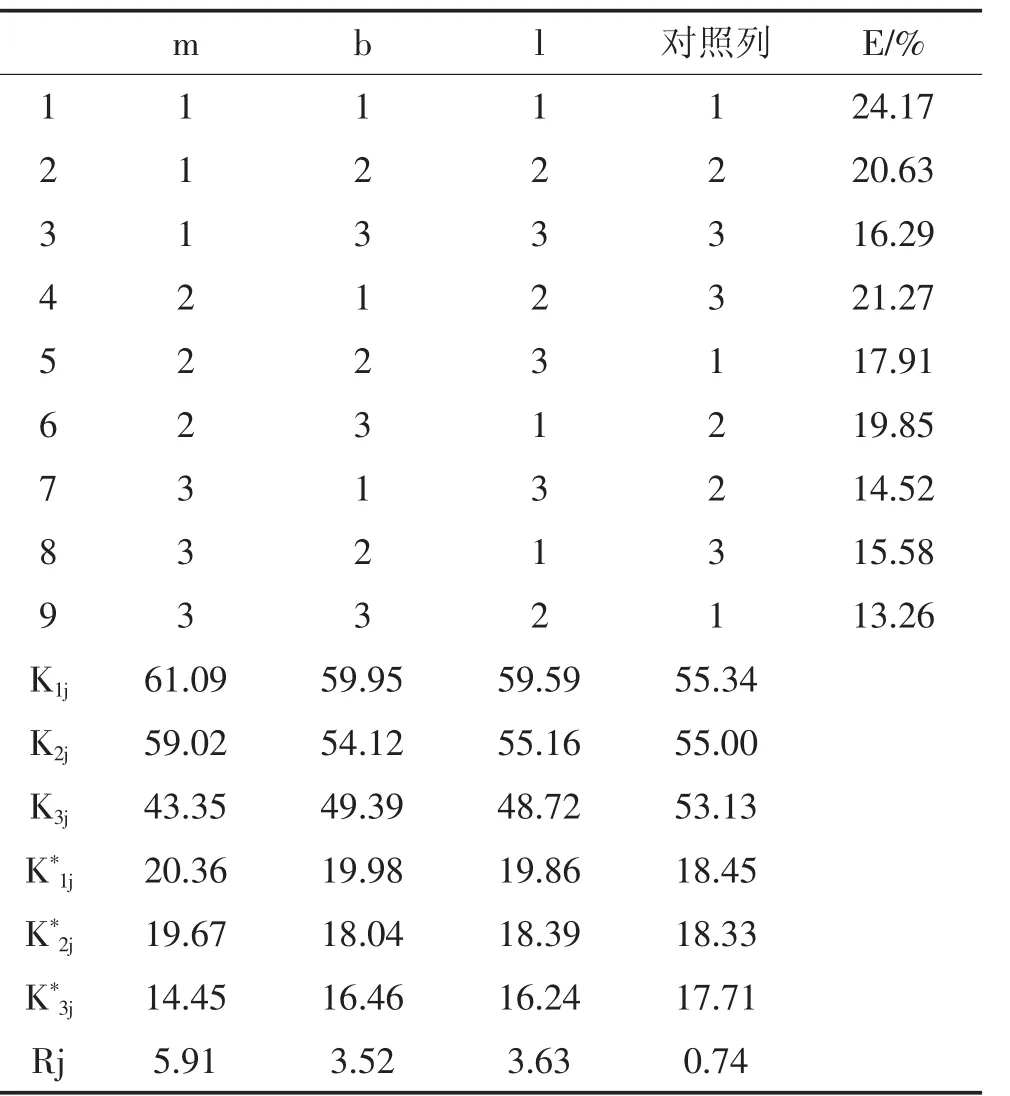
表4 極差分析結果

3.2 方差分析

方差分析過程的計算方法如下：

首先和方差分析步驟相同，計算Kij和K*ij。然后計算第j列K*ij的平均值K**ij為K**ij=1/nK*ij，n為第j列因素的水平數。由此可以計算出第j列的偏差平方和Sj=∑t(K*ij-K**ij)2，t為同一水平出現的次數。根據偏差平方和再計算方差Vj=Sj/fj，fj為自由度，fj=n-1。最后就可以計算F值：Fj=Vj/Ve，查F分布數值表作顯著性檢驗。

方差分析計算結果見表5。

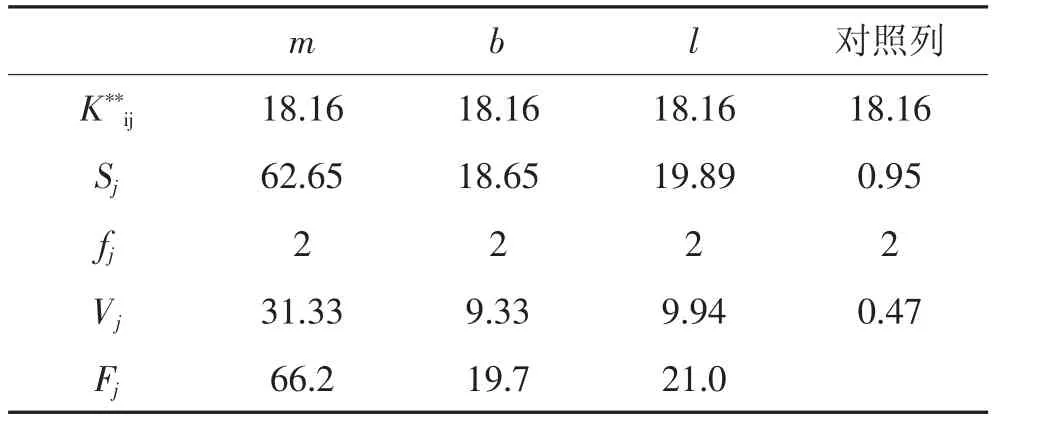
表5 方差分析結果

根據方差分析計算結果，查《F分布數值表》可知：

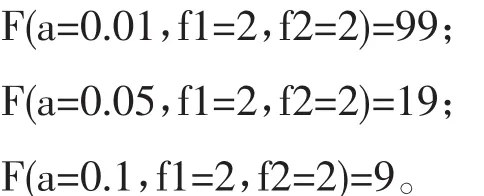
由表3-10的計算結果可知：對于第1列上的因素在α=0.01水平上顯著；第2、3列上的因素在α=0.05水平上顯著，因此實驗結果是可信的，即最優配置為 m1b1l1；三因素的主次順序為 m＞l＞b。

各因素和指標的關系變可通過因素-指標圖來描述。因素-指標圖，就是對每個因素以K*ij的值作為縱坐標，以因素水平作橫坐標作圖。

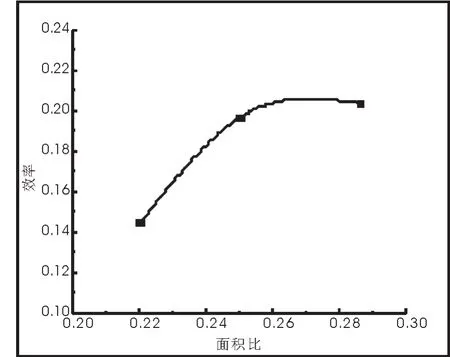
圖4 面積比與效率的關系

如圖4所示，實驗中，當面積比增加時，效率會隨之升高，因此最佳面積比應為最大值0.286，即m1水平。

如圖5所示，噴嘴角度變大時，效率隨之降低，這與孫妍等人[6]的實驗結果一致。最佳噴嘴角度為最小值 b1，為 10°。

如圖6所示，隨著喉嘴距的增加，效率呈下降趨勢，所以最佳喉嘴距為l1。實驗中采用的噴嘴內徑(d0)有3種，大致都在15mm左右，因此實驗結果確定的最佳喉嘴距為0.67d0，龍新平[10]等人通過研究得出的最優喉嘴距為0.5~1d0，兩者結果相符。

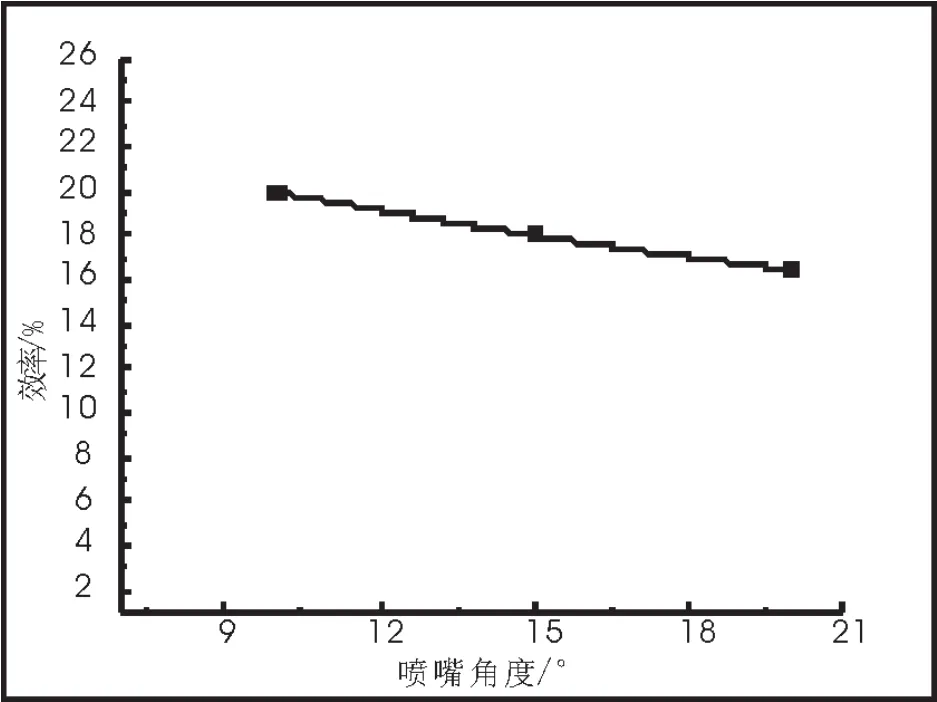
圖5 噴嘴角度與效率的關系

圖6 喉嘴距與效率的關系

4 實驗與理論的驗證

實驗中選取的面積比三水平分別為：0.286、0.25、0.22，實驗結果得出其中的最優值為0.286，而通過理論計算得出的最佳面積比為0.286，說明實驗結果和理論是相符的。

為進一步驗證，單獨考慮射流泵在面積比為0.286下的工作特性，將所得實驗值與理論值進行對比。

實驗過程中，固定射流管面積比為0.286，然后改變進口流量，進口流量從初始值450l/h開始，每次提升50l/h，一直增大到1000l/h為止。記錄實驗數據，整理結果見表6。

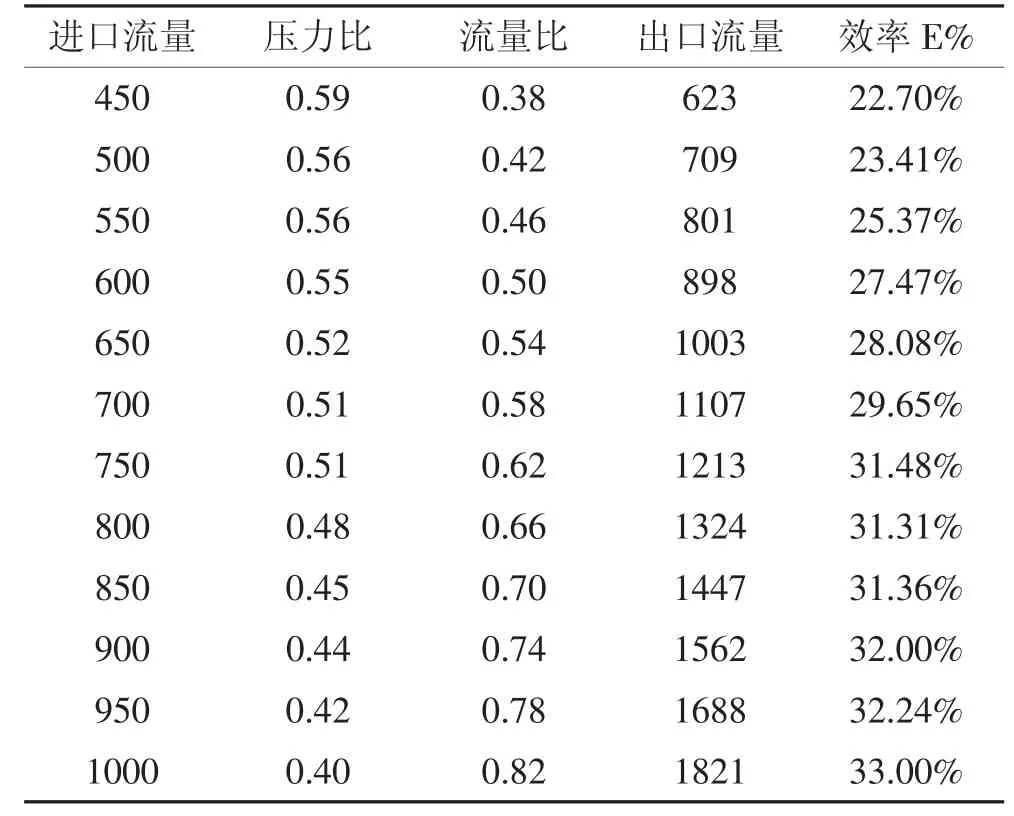
表6 實驗數據

整理數據，繪制對應的特性曲線，與理論值對比，結果如圖7和圖8所示。

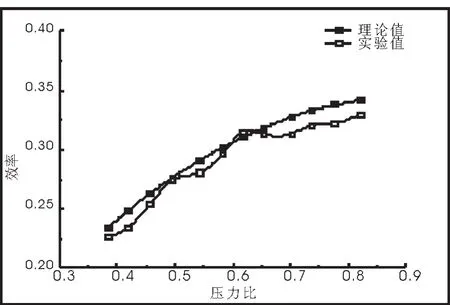
圖7 q-E特性曲線

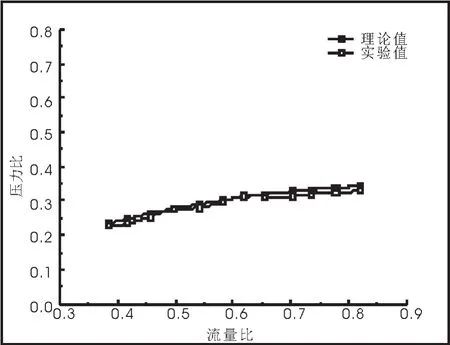
圖8 q-p特性曲線

從圖7、圖8中可以看出實驗結果和理論分析結果基本相符，驗證了理論分析的正確性。

5 結論

5.1 針對沉降槽中的射流管，根據能量平衡，推導了其基本特性方程，給出了一種射流管最優效率的設計方法。

5.2 對射流管進行了正交試驗研究，

確定了影響其效率的幾個主要因素的主次順序，即面積比＞喉嘴距＞噴嘴角度。

5.3 通過實驗對射流管的面積比進行了詳細分析，得出了特定條件下的最優面積比為0.286。

[1]Farrow J B.a new procedure for assessing the performance of flocculants.international journal of mineral processing,1996(46):263-275.

[2]White R B,TNguyen.Fluid flow in thickener feedwell models.Minerals Engineering,2003(16):145-150.

[3]Udman M R,Simic K,Paterson D A.Raking in gravity thickeners.international journal of mineral processing,2008(86):114-130.

[4]Mallela R,Chatterjee D.Numerical investigation of the effect of geometry on the performance of a jet pump.Professional Engineering,2011(c7).

[5]Yan Sun,Gui-jun Chen,Shuo Yin.he effect of inlet convergence angle on flow field and performance inside the jet pump.Proceedings 2011 Asia-Pacific Power and Energy Engineering Conference,2011,3-7.

[6]龍興平,程倩,等.射流泵最佳喉嘴距的數值模擬[J].核動力工程,2008(1).

（責任編輯：陳 輝）

The Study of Theoretical and Orthogonal Test on Jet Pipe in Settling Tank

WAN Xiao-li
（School of Mechanic Engineering,JiangXi University of Technology，Nanchang 330098,China）

This paper discusses the relevant parameters which affect the efficiency of a jet tube,ascertains that the area ratio is the most important parameter,and proposes a design method of determining optimal parameter of jet pipe.The effectiveness of this method is proved through orthogonal test.

settling tank；jet pipe；area ratio；orthogonal test

TF803.23

A < class="emphasis_bold"> 文章編號：1

123（2014）04-0040-06

2014-03-05

萬小立（1988-），女，湖北隨州人，江西科技學院機械工程學院，碩士。研究方向：熱能㈦動力工程。