一種基于聚類的非平衡分類算法

武永成，劉 釗

(1.荊楚理工學院 計算機工程學院，湖北 荊門 448000；2.武漢科技大學 計算機科學與技術學院，湖北 武漢 430081)

一種基于聚類的非平衡分類算法

武永成1，劉 釗2

(1.荊楚理工學院 計算機工程學院，湖北 荊門 448000；2.武漢科技大學 計算機科學與技術學院，湖北 武漢 430081)

傳統的分類算法大多假定用來學習的數據集是平衡的，但實際應用中真正面臨的數據集往往是非平衡數據。針對非平衡數據, 利用傳統的分類方法往往不能獲得良好的性能。文章提出了一種新的基于聚類的非平衡分類算法，通過聚類生成多個聚類體，在每個聚類體中選取一定數量的數據作為訓練樣本，有效地處理了樣例數據的不平衡問題，在相關數據集上的實驗驗證了本方法的有效性。

機器學習；非平衡分類；減重取樣；聚類

0 引言

分類(classification)是機器學習和數據挖掘中最典型的任務之一[1]。分類算法在對有標記樣本集合(或稱為有分類類型的樣本集合)進行分析和學習后，生成一個分類器。利用得到的分類器，可以對那些沒有分類類型的數據進行預測，判斷其分類類型。如醫務人員可以將病人的相關數據輸入分類系統，分類系統就能根據以往學習得到的分類器，自動判斷某個病人是否會藥物過敏。

傳統的分類算法很多都基于一種假定：用來學習的樣本數據都是平衡的，即各類樣本數據的數量差別不大，不是一類樣本數據的數量遠遠大于另一類數據。然而，現實世界中，很多情況下，樣例數據是不均衡的。例如：在1 000個體檢數據集中，最終分類類型為健康的可能占90%，分類類型為不健康的可能為10%，這樣的數據集就是非平衡的。本文中，為便于敘述，將一個數據集中大多數的樣例都屬于的分類類型稱為MA，而剩余的樣例的分類類型稱為MI。

對于非平衡數據的分類(imbalanced classification)，最大的問題是：最終得到的分類器可能只對MA數據敏感，而忽略MI數據。在對測試數據進行分類預測時，容易將其分類為MA而忽略MI。例如：銀行想利用分類算法構造一個分類器，對顧客未來是否進行信用貸款進行預測。銀行的歷史數據(有標記樣本集合)中，只有2%的顧客信用貸款，其余98%顧客不貸款。傳統的分類算法在這樣的樣本數據上進行學習得到的分類器，會將所有被預測的顧客判定為不貸款，因為這樣可以得到98%的分類準確率。顯然這不是銀行的真正目的。能對少數的可能貸款的用戶進行準確預測，才是銀行所需分類器的真正目的。

針對非平衡數據的分類，在監督學習中，主要采用的是重取樣(re-sampling)[2]和代價敏感(cost-sensitive learning)[3]的方法。

本文在重取樣技術的基礎上，提出了一種新的基于聚類(clustering)[1]的非平衡分類算法，通過聚類生成多個聚類體，在每個聚類體中選取一定數量有代表性的數據作為訓練樣本，有效地提高了對MI類數據預測的準確性。在相關數據集上的實驗驗證了本方法的有效性。

1 相關工作

機器學習的分類問題中，給定一個樣例集合D={,…}∈X×Y，其中是一個樣例。xi是一個向量[xi1,…xim]，yi是該樣例的標注(或分類類型)。X、Y分別是xi,yi的取值范圍。是未標注樣例，是有標注樣例。分類算法的任務就是在集合D上進行學習得到分類器。利用學習得到的分類器，就可以對未標注樣例的分類類型進行預測。

非平衡分類問題，作為一個具有挑戰性的機器學習問題，近些年在機器學習、數據挖掘等領域被廣泛研究。其中使用的最重要的技術是：重取樣技術和代價敏感學習技術。重取樣技術又分為增重取樣(over-sampling)[2]和減重取樣(under-sampling)[4]兩種方法，增重取樣技術通過復制MI樣本來使得它和MA的樣本數達到平衡，減重取樣技術則通過減少一定的MA樣本使它與MI的樣本數達到平衡。

減重取樣技術中最簡單的一種方法稱為隨機減重取樣技術(random under-sampling approach，簡稱為RUSA)，它隨機地在MA數據集中選取一定數量的MA樣本，與MI一起組成一個平衡的訓練集。

2 基于聚類的非平衡分類算法

隨機減重取樣技術最大的問題是隨機選取的樣本代表性可能不強。為此，本文提出了一種基于聚類的非平衡分類算法。首先對整個訓練集D(由MA樣本和MI樣本組成的非平衡數據集)進行聚類，生成若干個聚類體。對于這些聚類體，每個可能具有不同的特點。某個聚類體可能包含較多的MA樣本和較少的MI樣本，則這個聚類體的整體特性與MA樣本更接近；同樣，某個聚類體可能包含較多的MI樣本和較少的MA樣本，則這個聚類體的整體特性與MI樣本更接近。因此，根據每個聚類體中MA樣本與MI樣本的比值，我們的算法從每個聚類體中選取不同數量的MA樣本，與D中所有的MI一起，組成最終的訓練樣本D’(平衡的數據集)，這樣就有效地克服了隨機減重取樣技術的盲目性問題。

2.1 基于聚類的平衡數據集產生辦法

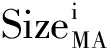
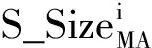
(1)

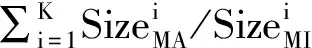
例如：有一個非平衡數據集D，它的樣本數量為1 100，其中SizeMA=1 000，SizeMI=100。聚類算法將D聚類為3個聚類體，3個聚類體的相關數據如表1所示。

設平衡化處理后的數據集D’中MA與MI樣本之比1∶1，則可知從D中選取的MA樣本數為100。這100個MA樣本，是分別從聚類體1、2、3中選取82、10、8個MA樣本組成的。具體計算方法如表2所示。

表1 3個聚類體的相關數據表

表2 3個聚類體中分別選取的MA樣本數

2.2 基于聚類的非平衡分類算法的完整描述

本文提出的基于聚類的非平衡分類算法，其完整描述如算法1所示。

算法1 基于聚類的非平衡分類算法

3 實驗結果與分析

實驗中用到兩個真實的數據集。一個是美國人口統計局1994年和1995年的人口-收入統計數據庫，該數據集中包含公民的年齡、性別、受教育程度、工作等信息，該數據集的任務是能對每個公民的收入進行預測。總樣本數為30 162，其中MA(收入低于5萬美元)樣本數為22 654，MI(收入高于5萬美元)樣本數為7 508；另一個數據庫是銀行貸款拖欠檢測數據集，該數據集中包含客戶基本信息、客戶支付能力和客戶賬單資金總量等信息，該數據集的任務是能對容易拖欠的客戶進行預測。該數據集的樣本總數為62 309，其中MA(不容易拖欠的客戶)樣本數為47 707，MI(容易拖欠的客戶)樣本數為14 602。我們使用80%的樣本作為學習樣本，其余20%的樣本用來對學習得到的分類器進行評價。

算法1的第一步提到的聚類算法采用k-medoids算法[6]，算法1的第四步提到的分類算法采用神經網絡算法[7]。

為驗證本算法的有效性，與隨機減重取樣算法(RUSA)進行了對比，實驗結果如表3所示。從表3可看出，在兩個數據集上，我們的算法都優于RUSA算法。

表3 兩種算法的實驗結果

4 結束語

本文針對隨機減重取樣技術的局限性，提出了一種基于聚類的非平衡分類算法。首先采用聚類算法對整個原始非平衡樣本集合進行聚類，得到多個聚類體；然后在每個聚類體中，選取一定數量的MA樣本，與原始樣本中的所有MI樣本一起，組成一個新的平衡的樣本集合。在該樣本集合上，利用傳統的分類算法進行學習，得到最終的分類器。在兩個非平衡數據集上，驗證了本算法的有效性。

[1] 韓家煒.數據挖掘:概念與技術[M].北京:機械工業出版社,2004.

[2] N Chawla,K Bowyer,L Hall,et al.SMOTE:Synthetic Minority Over-Sampling Technique[J].Journal of Artificial Intelligence Research,2002,16:321-357.

[3] Z Zhou,X Liu.Training Cost-Sensitive Neural Networks with Methods Addressing the Class Imbalance Problem[C]// IEEE Transaction on Knowledge and Data Engineering,2006:63-77.

[4] R Barandela,J Sánchez,V García,et al.Strategies for Learning in Class Imbalance Problems[J].Pattern Recognition, 2003,36:849-851.

[5] M Kubat,S Matwin.Addressing the Curse of Imbalanced Training Sets:One-Sided Selection[C]//In Proceedings of ICML-97,1997:179-186.

[6] Struyf A,Hubert M,Rousseeuw P.Integrating Robust Clustering Techniques in S-plus[J].Computational Statistics and Data Analysis,1997(26):17-37.

[7] Sondak N E,Sondak V K.Neural Networks and Artificial Intelligence[C]//In Proceedings of the 20th SIGCSE Technical Symposium on Computer Science Education,1989.

2013-11-05

武永成(1971-)，男，湖北仙桃人，荊楚理工學院講師，碩士。研究方向：機器學習和數據挖掘； 劉釗(1967-)，男，湖北襄陽人，武漢科技大學教授，博士。研究方向：人工智能和演化計算。

TP301.6

A

1008-4657(2014)02-0045-04

寸曉非]