反演變換求解二維調和方程的Dirichlet外問題

袁 萍

(長江大學文理學院 基礎課部，湖北 荊州 434020)

反演變換求解二維調和方程的Dirichlet外問題

袁 萍

(長江大學文理學院 基礎課部，湖北 荊州 434020)

在研究靜電場的電位函數、平穩狀態下的波動現象和擴散過程時都會遇到調和方程。反演變換又稱逆矢徑變換，是一種很有效的數學方法。文章首先給出反演變換的定義及性質，然后推導了平面區域上二維調和函數的積分公式，最后利用反演變換將調和方程的Dirichlet外問題化為內問題，得到了二維調和方程圓域外Dirichlet問題的解。

調和方程；反演變換；Dirichlet外問題

0 引言

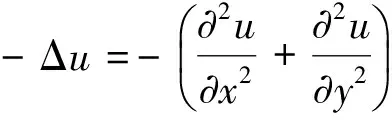
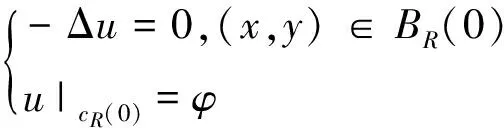
1 反演點與反演變換

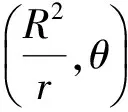
2 二維調和方程Dirichlet內問題的積分表達式

(1)

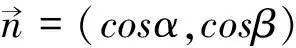
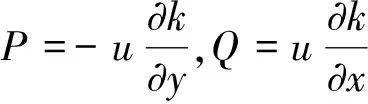
(2)

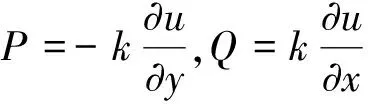
(3)

(2)與(3)相減得格林第二公式

(4)

由于k(r)在P0處有奇性，需要在D中挖去一個小圓域，以P0為圓心、任意小的ρ為半徑做圓域Bρ(P0)。

在區域DBρ(P0)中應用格林第二公式有：

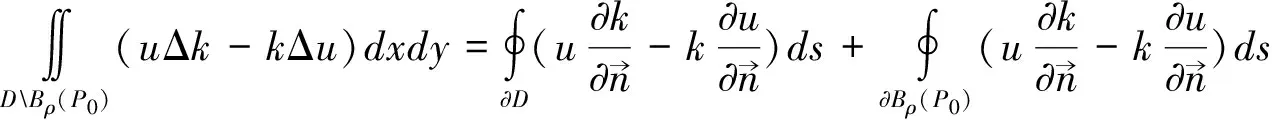
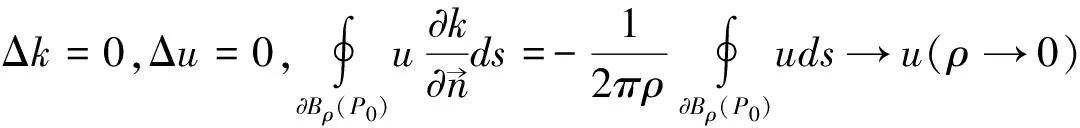
(5)

(6)

(5)與(6)相加得

(7)

記G(r)=k(r)+h(r)，則(7)式為

(8)

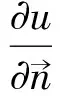
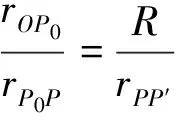
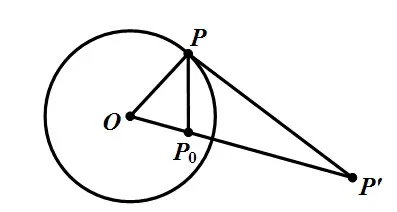
圖1 靜電源像法求圓域上的格林函數

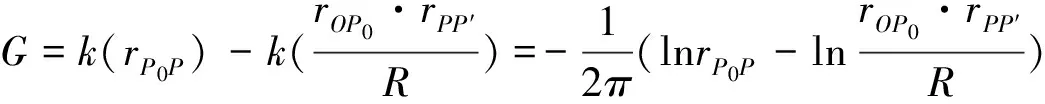
(9)

3 利用反演變換將圓域Dirichlet外問題化為內問題

設所給Dirichlet外問題為

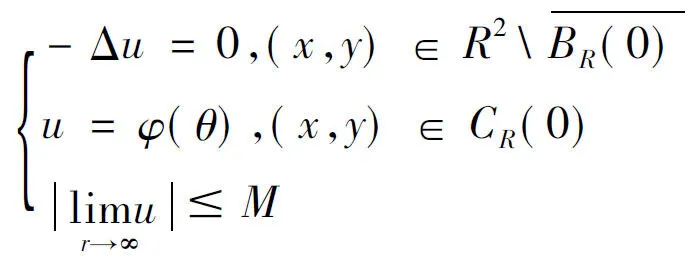
(10)

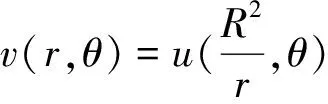
利用復合函數求導法則，得

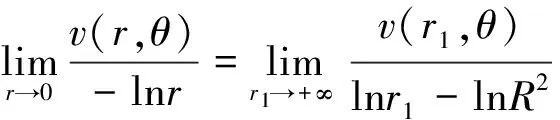
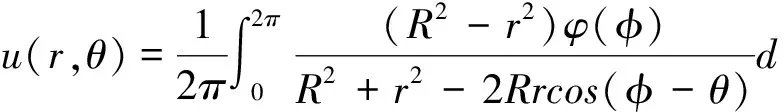
其中(r,θ)為圓域內點的極坐標，(R,φ)為CR(0)上點的極坐標。

[1] 谷超豪.數學物理方程[M].2版.北京:高等教育出版社,2002.

[2] 王明新.偏微分方程基本理論[M].北京:科學出版社,2009.

[3] 于濤.數學物理方程與特殊函數[M].哈爾濱:哈爾濱工程大學出版社,2006.

[4] 劉連璞.平面解析幾何方法與研究[M].北京:北京大學出版社,1999.

[5] 倪秀芳,李祥林.復平面上反演變換的性質[J].阜陽師范學院學報:自然科學版,1994(2):42-46.

[6] 陸靜.用格林函數法求解二階微分方程邊值問題[J].太原師范學院學報,2011,10(4):32-36.

2014-03-04

袁萍(1984-)，女，湖北潛江人，長江大學文理學院講師，碩士。研究方向：偏微分方程。

O175.2

A

1008-4657(2014)02-0057-03