積分方程組解的正則性與對稱性

王長森，林國煒

(江西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，330022，南昌)

積分方程組解的正則性與對稱性

王長森，林國煒

(江西師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，330022，南昌)

將討論下列含貝塞爾核積分方程組正解的對稱性，即：

(1)

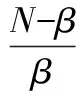
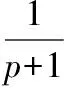
(2)

設(shè)(u,v)∈Lp+1(RN)×Lq+1(RN)為式(1)的正解，則式(1)解是徑向?qū)ΨQ的。

積分方程組；貝塞爾核；徑向?qū)ΨQ

0 引言

本文將討論下列含貝塞爾核積分方程組正解的對稱性，即：

(3)

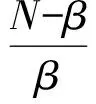
(4)

特別的，當u=v,p=q,β=τ=0時，式(3)簡化成：

(5)

在文獻[8]中，對于貝塞爾勢能的sobolevinepuality(Bα(f)=Gα*f,α>0;Bα(f)=f,α=0,這里*表示函數(shù)間的卷積)：

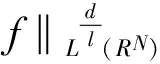
(6)

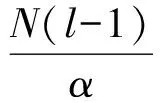
當β=τ=0時，在文獻[9]中討論了方程組(3)正解的徑向?qū)ΨQ性，同時也討論了當α=2,β=τ=0時解的唯一性。如果β≠0,τ≠0時，在文獻[9]中建立了關(guān)于貝塞爾勢能帶雙權(quán)Hardy-Littlewood-Sobolevinequality，即：

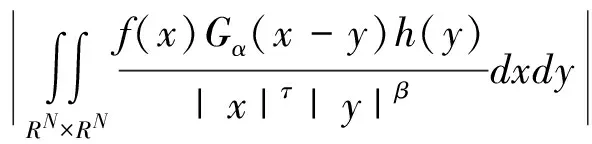
(7)

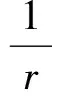
在文獻[6]中已證出下面積分方程組：

(8)

正解的徑向?qū)ΨQ性和局部H?lder連續(xù)性。

式(3)是關(guān)于式(7)的Euler-Lagrange方程。為了得到不等式式(7)中的最佳常數(shù)，定義最大函數(shù)：

在‖f‖r=‖h‖s=1的條件下，則對應(yīng)的Euler-Lagrange方程為下面積分方程組：

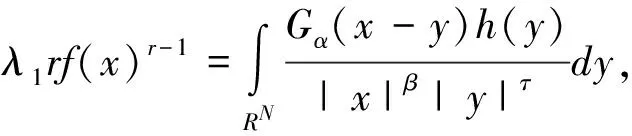
(9)

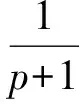
當貝塞爾核Gα(x)可以被Riesz核替代時，則式(3)就化成：

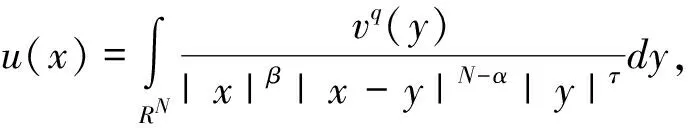
(10)

(11)

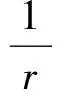
在文獻[4]中，通過移動平面法已證出方程組(10)正解的徑向?qū)ΨQ性。此外，研究者也采用在文獻[7]中的正則性提升方法，得出理想的積分區(qū)間和漸近性，讀者可以查閱在文獻[1-3,5,7,13-14]中更多的應(yīng)用。

本文主要討論在式(4)條件下，式(3)正解的徑向?qū)ΨQ性，即：在(u,v)∈Lp+1(RN)×Lq+1(RN)為式(3)的正解，則解(u,v)是徑向?qū)ΨQ的。

1 引理及其命題

對于任意的實數(shù)λ，定義：∑λ={x=(x1,x2,…,xN)∈RN|x1≤λ},Tλ={x∈RN|x1=λ}。對于x∈∑λ，令xλ=(2λ-x1,x2,…,xN)，定義：uλ(x)=u(xλ),vλ(x)=v(xλ)。

引理1：對于式(3)的任意正解，有：

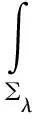
(12)

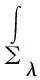
(13)

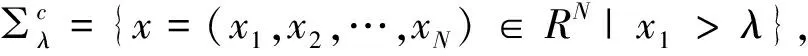
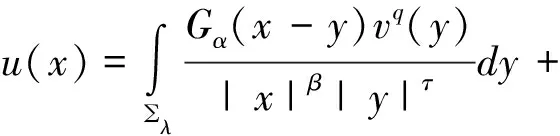
在上等式中應(yīng)用了在RN中Gα是徑向?qū)ΨQ的，即有|xλ-y|=|x-yλ|，在上等式中x用xλ代替有：

因此，

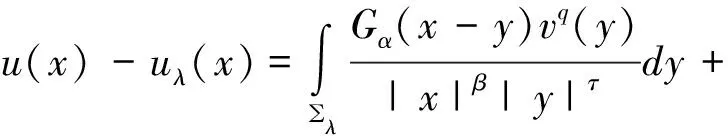
同理，v(x)-vλ(x)也是成立的。證畢。

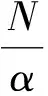
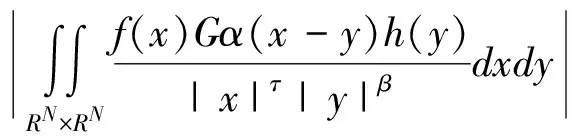
(14)

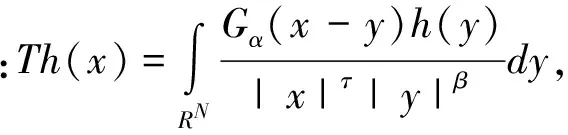
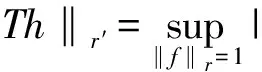
(15)

此命題的證明可參考文獻[6]。