節理巖體巷道的穩定性分析

王 文，朱維申，陳云娟，張 磊

(山東大學 巖土與結構工程研究中心，山東 濟南 250061)

節理巖體巷道的穩定性分析

王 文，朱維申，陳云娟，張 磊

(山東大學 巖土與結構工程研究中心，山東 濟南 250061)

由于節理、斷層等不連續面的存在造成巖體變形的不連續性，并且這些不連續面對巖體變形、應力等力學行為造成重要影響。對已有的非連續變形分析程序進行了兩點改進，分別在程序中加入了錨桿的塑性模擬和改進的SSOR-PCG方法，并且通過與試驗數據的對比驗證了改進程序的正確性。分析了某節理巖體巷道圍巖的破壞過程，得到在原來支護方式的基礎上在頂拱應力集中的位置增加3根錨索的支護方式對巷道的支護效果較好。最后通過對巷道關鍵點位移的監測優化了支護參數，得到錨桿長度為 3 m，施加預應力為120kN為支護的最優方式。

節理巖體；圍巖穩定性；非連續變形分析方法；錨固效應;裂隙擴展

目前，以有限元法和有限差分法為代表的計算方法在巖土工程穩定評價中廣泛應用。但是，巖體作為一種地質結構體，這些基于連續介質的數值方法在模擬巖體的變形與穩定方面存在一定的局限性，因此，一些考慮巖體非連續性特點的數值方法，包括關鍵塊體理論、離散元法、不連續變形分析方法等，自20世紀80年代開始逐步受到巖石力學界的關注和重視。非連續變形分析方法DDA(discontinuous deformation analysis)是由石根華博士提出的分析塊體運動和變形的一種數值方法[1-2]，該方法基于最小勢能原理建立系統方程，具有完備的塊體運動學理論，能夠較好地模擬多塊體系統的大位移和大變形問題，因此在數值模擬和工程應用方面取得了較大的發展。鄭榕明等詳述了有限元與DDA的耦合算法，并給出了計算實例，證明了耦合方法的優越性[3];姜清輝[4]和劉君等[5]研究了三維DDA模型，編制了相應的 DDA 程序；鄔愛清等[6]應用DDA對復雜地質條件下地下廠房圍巖的變形與破壞特征開展了研究；馬永政等[7]在DDA程序中引進無網格節點位移插值模式；姜清輝等[8]對DDA采用的常加速度法進行拓展，給出求解塊體系統運動方程的 Newmark積分格式，并引入一種與塊體不平衡力成正比的自適應阻尼，保證求解的穩定性；高亞楠等[9]采用有限變形理論對現有的DDA程序進行了改進，拓寬了DDA的使用范圍；劉永茜等[10]在DDA中考慮了慣性力和阻尼力作用，并改進時間步長自動調節;焦玉勇教授等[11]改進了DDA方法，提出一種可用來模擬節理巖體的斷裂破壞過程的新方法——DDARF(discontinuous deformation analysis for rock failure)。筆者對原有 DDARF程序進行了兩點改進，方程迭代采用改進的SSOR-PCG方法進行，并且在程序中考慮了錨桿的塑性變形。應用改進的計算程序對某節理巖體巷道的支護方案和支護參數進行了優化分析，研究成果為正在開工的巷道的施工和設計者提供了參考。

1 DDARF的基本理論

DDARF方法是基于改進的DDA方法，用來解決斷續節理巖體的破壞問題。該方法[12-13]采用行波法將計算區域自動剖分成三角形塊體單元，塊體邊界分為真實節理邊界和虛擬節理邊界。對于模型中的所有節理，在沒有達到斷裂破壞準則時都將其定義為虛擬節理，其強度在計算過程中達到斷裂破壞準則后則轉化為真實節理，形成裂隙，并對其賦以真實的節理強度參數。裂紋擴展沿虛擬節理進行并且按照界面破裂準則進行開裂。虛擬節理的破壞分為拉伸破壞和剪切破壞兩種，拉伸破壞采用最大拉應力準則，剪切破壞采用摩爾-庫侖準則。斷續節理的變形、破壞過程可認為是虛擬節理的開裂、擴展和貫通，在這一過程中伴隨著虛擬節理力學屬性(黏聚力、內摩擦角、抗拉強度)減弱、斷續節理整體強度降低。因此，DDARF方法可以模擬裂紋萌生、擴展、貫通和巖體破碎全過程，適用于完整巖石、斷續節理巖體乃至完全不連續巖體等任意情形。

2 錨桿的錨固效應

筆者對原來的錨桿模型進行了改進，考慮了錨桿的塑性。

2.1 錨桿的塑性模擬

對錨桿的數值模型做如下簡化：① 錨桿主要承受軸向作用力。② 假定錨桿為理想彈塑性體，Tyield為錨桿的抗拉強度。當軸力fTanch，則置f=0。

考慮有一根錨桿連接塊體i的點(x1，y1)與塊體j的點(x2，y2)，如圖1所示，設錨桿有預應力fa，錨桿的剛度為e。記錨桿長度為l，錨桿兩端點位移分別為{u1，v1}和{u2，v2}，則

(1)

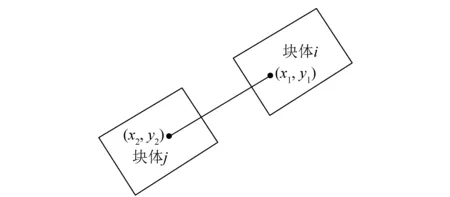
圖1 錨桿示意Fig.1 Anchor schemes

錨桿的伸長量可表示為

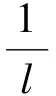
y2)(dy1-dy2)]=

(2)

式中,lx，ly為錨桿的方向余弦，其表達式為

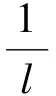
若錨桿有預應力，則錨桿的總伸長量為

(4)

則錨桿的應變能為

(5)

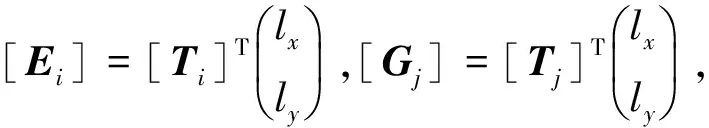
(6)

當f≥Tyield時，錨桿的勢能Πb為

(7)

在程序中對錨桿進行判斷，然后分別對式(6)，(7)求導使其最小化，疊加到總體平衡方程中即可以得到錨桿的錨固效應。

2.2 劈裂條件下裂隙試塊的錨固效應

為了驗證錨桿模型的正確與否，筆者對含裂隙的巖體進行了錨固，利用數值模擬方法對試塊的強度和裂紋擴展過程進行了研究，然后與試驗進行了對比分析。

2.2.1模型建立

張磊[14]對劈裂試驗中錨固裂隙試塊的強度和裂紋擴展過程進行了試驗研究。參照他的試驗，筆者擬采用DDARF程序進行數值模擬的相似研究，并與其結果進行對比分析。首先建立與劈裂試驗有相同尺寸的模型并且施加相同的軸向位移荷載，然后分別研究錨固角(錨桿埋設方向與裂隙平面所形成的銳角)為30°，45°，70°和85°四種工況下的裂隙對試塊性能的影響。為了使試驗中的錨桿屈服，進而可以對比數值模擬和試驗結果，程序中增加了計算時步，使錨桿進入了塑性區。

2.2.2數值模擬結果

使用DDARF程序模擬出錨固角度為30°的試塊的軸向荷載-位移變化曲線。由于程序中不能模擬錨桿的滑移，因此試塊破壞后軸向荷載-位移曲線中沒有出現殘余強度，如圖2所示。錨固角度為30°的試塊的裂紋擴展過程如圖3所示：加錨后，試塊首先在裂隙尖端產生翼裂隙，然后許多次生裂紋在兩個相鄰端開始產生并擴展，并且相向生長，隨后形成破碎帶而導致試塊破壞。

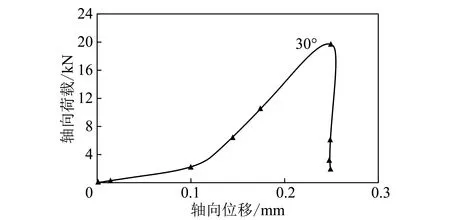
圖2 軸向荷載-位移曲線Fig.2 Axial load-displacement curves

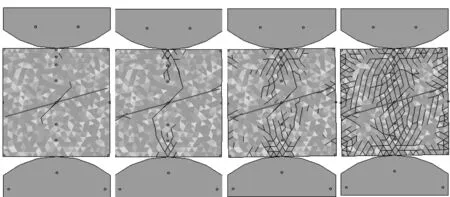
圖3 裂紋擴展過程Fig.3 Propagation process for fractures

2.2.3試驗分析

張磊[14]研究了劈裂條件下不同錨固角度的錨桿對裂隙試件的錨固效應。試驗中采用硬鋁合金棒作為錨桿材料(圖4(a))，并采用厚度為1mm，寬度為4cm，長度為15cm的聚氯乙烯薄膜加工的薄片作為預置貫穿裂隙(圖4(b))。試塊為邊長100mm的立方體，裂隙與軸向的夾角分別為30°，45°，70°，85°。

圖4 錨桿、裂隙材料和劈裂試驗裝置Fig.4 Anchor and fissure materials and splitting test device

劈裂試驗是將試件放置于劈裂夾具中完成的(圖4(c))。試驗過程中采用位移控制方式，在伺服壓力機上以一定的加載速率對劈裂夾具加載，直至試件發生劈裂破壞。

2.2.4試驗結果

通過劈裂試驗分別得到錨固角度為30°的試塊軸向荷載-位移變化曲線和破壞過程，如圖5和6所示(圖6中的圓圈表示錨桿)。圖5中的軸向荷載峰值點A的值見表1。試塊破壞過程如下：隨著荷載的增大，裂縫發展程度增加，隨后錨桿與砂漿在黏結界面上發生滑移，錨桿屈服，最后試件徹底斷裂。

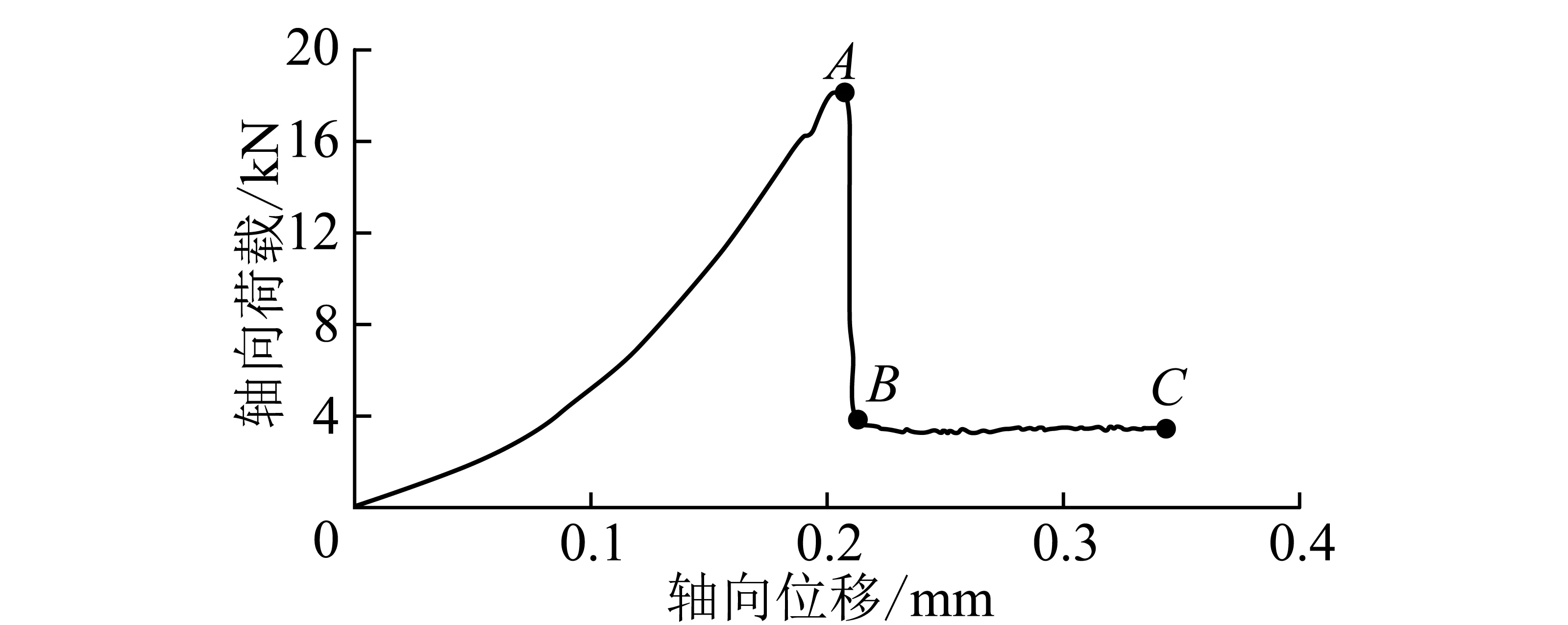
圖5 劈裂試驗中軸向荷載-位移曲線Fig.5 Axial load-displacement curve in splitting test

圖6 試驗中裂紋擴展過程Fig.6 Crack propagation process in splitting test

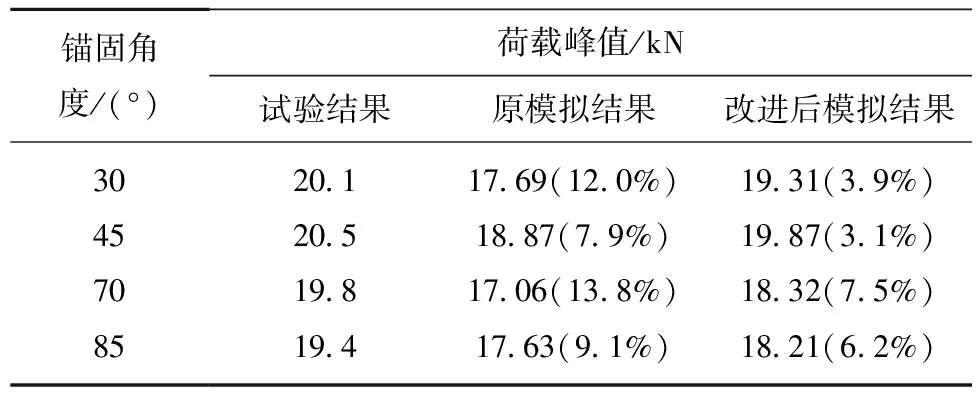
表1 錨固試塊的峰值強度Table 1 Peak strength of anchor specimens

2.2.5結果對比分析

將DDARF數值模擬計算結果與室內劈裂試驗結果進行對比，見表1(括號中的數值表示該數據比試驗數據的減少量占試驗數據的百分比)可知：軸向荷載-位移曲線的峰值強度相差幅度在1%～15%，模擬效果較好。同時，數值模擬的裂紋擴展規律也與試驗現象相符。由表1也可以得到錨桿的塑性模型可以更加精確地模擬錨桿對節理巖體的加固作用，表明這種方法對錨桿的模擬是正確的。

3 改進的SSOR-PCG方法

最初非連續變形方法方程迭代采用了直接解法和逐步超松弛(SOR)迭代法。塊體較少時，可采用直接解法，塊體較多時，采用SOR迭代法。SOR法需要一個松弛因子，它的選取對計算效率是至關重要的，但是最佳的松弛因子又無法確定，這無疑影響了非連續變形方法的使用。考慮到平衡方程中K陣的對稱、正定、主元占優的特點，筆者采用預處理共軛梯度法(PCG)，用K陣的對角陣作為預處理矩陣。如果將PCG與SSOR(對稱逐步超松弛)相結合，可以得到非常有效的SSOR-PCG法。它具有SSOR對松弛因子的不敏感性和PCG收斂速度快的特點。筆者將改進后的SSOR-PCG方法[15]加入到DDARF程序中，節省了方程的計算量，加快了計算效率，可比原迭代方法節省計算量8%～50%[16]。

4 工程中的實際應用

在煤礦巷道支護工程中，支護方式的選擇及支護參數的確定往往是重點考慮的問題，可以達到提高支護效果的目的，對煤礦節省成本，提高經濟效益，具有重要應用價值。現以某煤礦的水平運輸大巷為例，利用改進后的數值模擬軟件DDARF研究了巷道圍巖的裂紋擴展過程，改進了支護方式，優化了支護參數，為現場的施工與設計提供了一定的理論指導。

4.1 模型的建立

煤礦的半圓拱形巷道斷面外接于半徑為1.5m 的圓。巷道問題符合平面應變問題，故建立平面模型進行模擬，選取煤礦巷道比較有代表性的局部區域進行模型計算，模型的寬、高分別是巷道寬、高的10倍。模型的上表面施加均勻的垂直壓應力，模型兩側面施加隨深度變化的水平壓應力，模型下表面的垂直和水平位移固定。該大巷圍巖在開挖后出現破裂巖體，主要以泥巖、粉砂巖為主，并夾有多層小煤及煤線，而且附近還有小斷層，巖層非常破碎。因此筆者根據地質條件，運用蒙特卡洛方法，生成隨機節理，推演了更小規模的節理的空間分布。巷道模型和加載方式如圖7所示。

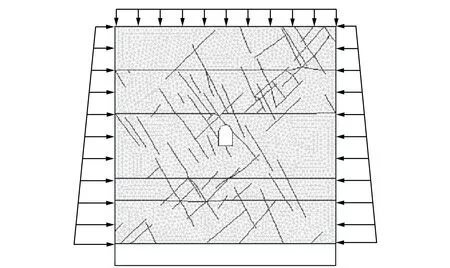
圖7 巷道的計算模型和加載方式Fig.7 The computation model and load method of the roadway

4.2 力學參數和收斂準則

在巖體工程穩定性分析中，力學參數選取將對計算結果產生很大的影響，本次計算模型力學參數根據現場位移反分析所得結果，并參考巖塊試驗得到，見表2,3。

表2巖體力學參數
Table2Mechanicalparametersoftherockmass

名稱彈性模量/GPa泊松比內摩擦角/(°)黏聚力/MPa容重/(kN·m-3)中粒粗砂巖3 80 2130225 4粉砂巖1 60 27271 725 0煤0 70 35200 415 6泥頁巖0 80 32251 321 0細砂巖3 20 23293 225 3

表3巖體界面的力學參數
Table3Mechanicalparametersoftheinterfaceoftherockmass

內摩擦角/(°)黏聚力/MPa抗拉強度/MPa3021

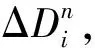
4.3 巷道支護方案的優化

4.3.1巷道圍巖的破壞過程

采用屏幕錄像專家軟件記錄DDARF程序計算過程，得到直墻半圓拱形巷道圍巖的破壞過程，如圖8所示：在巷道底板處，隨著底角破壞程度的增加，底板跨度不斷增大，引起底板變形。然后巷道底角處破壞，引起兩幫承載能力降低，進而導致頂板變形量加大。同時數值模擬和工程實際情況均表明巷道圍巖兩幫及頂底板位移量并不是均勻的，而是首先從巷道某一個部位開始破壞，從而導致整個巷道支護體失穩，直墻半圓拱巷道周圍形成“雙耳”是應力集中關鍵部位。

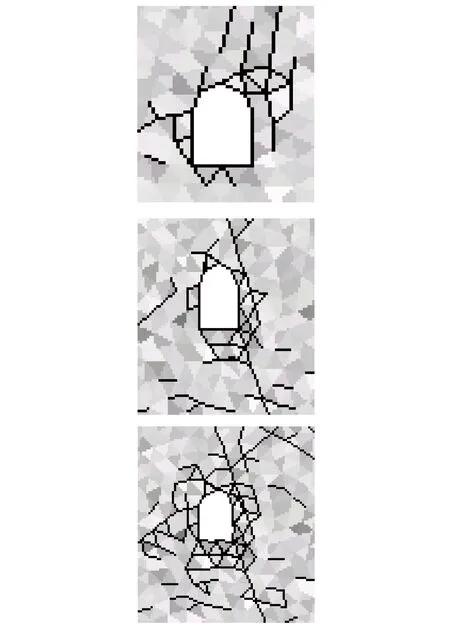
圖8 圍巖的破壞過程Fig.8 The damage process of surrounding rocks

4.3.2巷道支護方式優化

由于受斷層影響，局部地段頂煤節理裂隙發育，幫頂圍巖松軟易碎，頂板及肩角處下沉明顯，圍巖產生不連續變形(圖8)。根據巷道的破壞過程，原設計中采用錨桿支護，如圖9(a)所示。其中錨桿采用φ25mm的強力錨桿，長度為3 m，彈性模量為200GPa，預應力為120kN，屈服強度600MPa。施加錨桿后，邊墻和頂部的位移都減小，但是頂板的應力集中程度也是比較高，底板無支護，造成底臌。筆者在原設計的基礎上改變了巷道圍巖的支護方式，采取在頂部應力集中關鍵點上施加錨索(圖9(b))。其中錨索采用直徑19mm的鋼絞線，極限拉斷力400kN，長度為6 m。3根錨索的功能各不相同，中間錨索是控制頂板位移的，而兩邊的錨索是轉移上覆巖層應力到深部去；底角錨桿是控制底臌的，它能有效控制巷道兩幫的水平擠壓力，從而有效控制底臌。由圖9可知施加錨索后，巷道周邊的應力集中現象得到改善，應力分布更加均勻，表明錨索調動了深部巖體強度，控制了淺部巖體的穩定性。

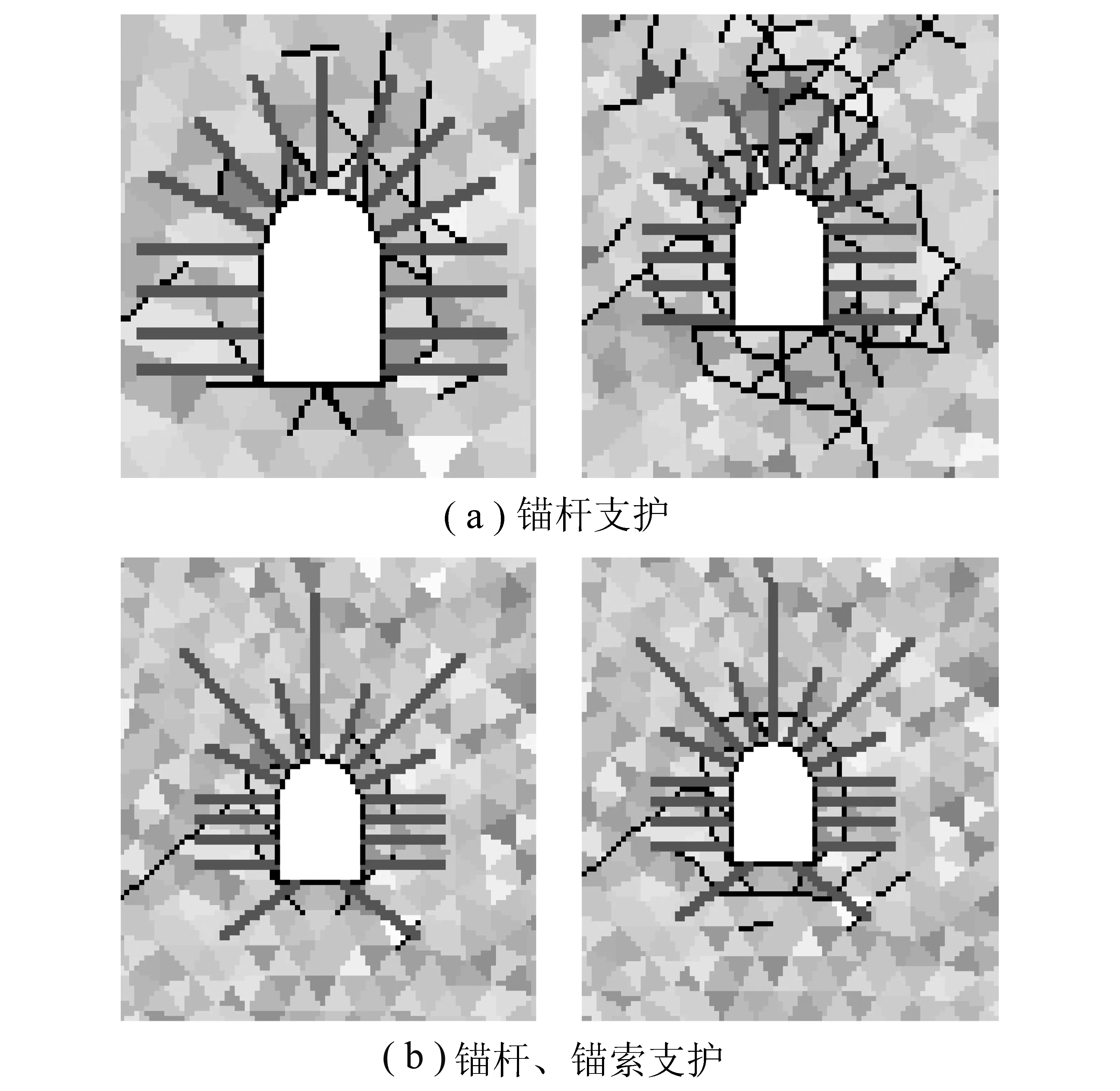
圖9 巷道支護和破壞Fig.9 The diagrams of support of roadways and damage

不同支護方式下關鍵點的位移值見表4(括號中的數值表示該數據比無錨桿數據減少量占無錨桿數據的百分比)。可以看出：加錨桿后，巷道的頂拱、幫部和底板的位移值都比無錨支護時位移值小，減小幅度為10%～20%；錨桿錨索聯合支護后，巷道的頂拱、幫部和底板的位移值比無錨支護時的減小20%～30%。由此可見當錨桿、錨索的預應力產生協同作用時，對深部巷道的支護效果明顯，有效地阻止了巷道圍巖的變形，控制了巷道的破壞。因此，錨桿-錨索-圍巖共同承載的支護方式可以維護巷道的安全穩定，值得推廣。

表4不同支護方式下關鍵點的位移
Table4Comparisonofdisplacementsofkeypointsmm

工況頂拱左幫中點底板中點無錨桿-1085146 3錨桿效應-92(14 8%)43(15 7%)40(13 6%)錨桿錨索效應-80(25 9%)37(27 5%)36(22 2%)

4.3.3支護參數的優化

(1)錨桿預應力值的選擇。

在基本模型其他參數不變的條件下，通過改變錨桿和錨索的預應力值[17](60，90，120，150，180kN)得到其對巷道圍巖位移的影響變化曲線，如圖10(a)所示。

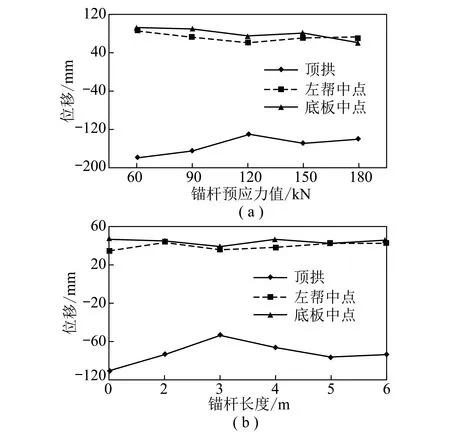
圖10 錨桿預應力，錨桿長度與位移關系曲線Fig.10 Relation curves of prestress and length of the rock bolt with displacement

由圖10(a)可見，隨著錨桿預應力的增加，圍巖的位移值減小，但是預應力值為120kN后再增加預應力值圍巖的位移量的改變不是很大，所以在本工程中施加預應力為120kN比較合適。

(2) 錨桿長度的選擇。

在基本模型其他參數不變的條件下，通過改變錨桿長度(2，3，4，5，6 m)得到其對巷道圍巖位移的影響變化曲線，如圖10(b)所示。

由圖10(b)可見，錨桿長度影響著地下工程位移量及圍巖穩定性，且錨桿長度為3 m時圍巖的位移較小。錨桿長度若再增大，將造成浪費，而且也不必要，所以在本工程中錨桿長度為3 m比較合適。

5 結 論

(1)在劈裂試驗中，通過DDARF數值模擬與室內試驗進行對比得到：荷載-位移曲線的峰值強度較一致，數值模擬的裂隙擴展規律也與試驗現象相符。同時通過試驗驗證了錨桿塑性模型的正確性，可以更加精確的模擬錨桿對節理巖體的加固作用。

(2)采用位移收斂準則計算某個工程收斂的時間和收斂時步，得到改進的SSOR-PCG收斂方法可以節省方程的計算量，加快計算效率，大大的提高程序的計算速度。

(3)巷道圍巖采用錨桿-錨索-圍巖共同承載的支護方式，對深部巷道的支護效果明顯，控制了巷道的底臌，改善了巷道周邊的應力集中，并且減少了巷道圍巖的變形。

(4)通過對巷道支護參數的優化分析，本工程中選取錨桿長度3 m，施加預應力為120kN比較合適，巷道圍巖的穩定性較好。

[1] Shi G H.Discontinuous deformation analysis:a new numerical model for the statics and dynamics of block system[D].Berkeley：University of California,1988.

[2] Chang T C.Nonlinear dynamic discontinuous deformation analysis with finite element meshed block systems[D].Berkeley:University of California,1994.

[3] 鄭榕明，張勇慧，王可鈞.耦合算法原理及有限元與DDA 的耦合[J].巖土工程學報,2000,22(6):727-730. Zheng Rongming,Zhang Yonghui,Wang Kejun.Coupling of FEM and DDA method[J].Chinese Journal of Geotechnical Engineering,2000,22(6):727-730.

[4] 姜清輝.三維非連續變形分析方法的研究[D].武漢:中國科學院武漢巖土力學研究所,2000.

[5] 劉 君.三維非連續變形分析與有限元耦合算法研究[D].大連:大連理工大學,2001.

[6] 鄔愛清,丁秀麗,陳勝宏,等.DDA 在復雜地質條件下地下廠房圍巖變形與破壞特征分析中的應用研究[J].巖石力學與工程學報,2006,25(1):1-8. Wu Aiqing,Ding Xiuli,Chen Shenghong,et al.Researches on deformation and failure characteristics of an underground powerhouse with complicated geological conditions by DDA method[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(1):1-8.

[7] 馬永政,鄭 宏,李春光.應用自然鄰接點插值法的塊體非連續變形分析[J].巖土力學,2008,29(1):119-124. Ma Yongzheng,Zheng Hong,Li Chunguang.Applying natural neighbor interpolation to discontinuous deformation analysis of block system[J].Rock and Soil Mechanics,2008,29(1):119-124.

[8] 姜清輝，周創兵，漆祖芳.基于Newmark積分方案的DDA方法[J].巖石力學與工程學報,2009,28(1):2778-2783. Jiang Qinghui，Zhou Chuangbin，Qi Zufang.Discontinuous deformation analysis method besed on newmark integration algorithm[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):2778-2783.

[9] 高亞楠，高 峰，Man-chu Ronald YEUNG.基于有限變形理論的非連續變形分析方法改進[J].巖石力學與工程學報,2011,30(11):2360-2365. Gao Yanan，Gao Feng，Man-chu Ronald YEUNG.Modification of discontinuous deformation analysis method based on finite deformation theory[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(11):2360-2365.

[10] 劉永茜，楊 軍.一種改進步長自調的非連續變形分析法[J].巖土力學,2011,32(8):2544-2548. Liu Yongqian,Yang Jun.An improved DDA method with adaptive step size[J].Rock and Soil Mechanics，2011,32(8):2544-2548.

[11] 焦玉勇，張秀麗，劉泉聲,等.用非連續變形分析方法模擬巖石裂紋擴展[J].巖石力學與工程學報,2007,26(4):682-691. Jiao Yuyong,Zhang Xiuli,Liu Quansheng,et al.Simulation of rock crack propagation using discontinuous deformation analysis[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(4):682-691.

[12] 張秀麗.斷續節理巖體破壞過程的數值分析方法研究[D].武漢:中國科學院武漢巖土力學研究所,2007.

[13] 張秀麗,焦玉勇,劉泉聲,等.用改進的DDA方法模擬公路隧道的穩定性[J].巖土力學,2007,28(8):1710-1714. Zhang Xiuli,Jiao Yuyong,Liu Quansheng,et al.Modeling of stability of a highway tunnel by using improved DDA method[J].Rock and Soil Mechanics,2007,28(8):1710-1714.

[14] 張 磊.錨桿加固對裂隙巖體力學性能影響的室內試驗和數值分析[D].濟南:山東大學,2009.

[15] 林紹忠.對稱逐步超松馳預處理共軛梯度法的改進迭代格式[J].數值計算與計算機應用,1997,18(4):266-270. Lin Shaozhong.Improved iterative format of symmetric successive over relaxation-preconditioned conjugated gradient mthod[J].Journal of Numerical Methods and Computer Applications,1997,18(4):266-270.

[16] 林紹忠.用預處理共軛梯度法求解有限元方程組及程序設計[J].河海大學學報,1998,26(3):112-115. Lin Shaozhong.Application of preconditioned conjugated gradient method to finite element equations and program design[J].Journal of Hehai University,1998,26(3)：112-115.

[17] 康紅普，姜鐵明，高富強.預應力錨桿支護參數的設計[J].煤炭學報,2008,33(7):721-726. Kang Hongpu，Jiang Tieming，Gao Fuqiang.Design for pretensioned rock bolting parameters[J].Journal of China Coal Society,2008,33(7):721-726.

Analysisofroadwaystabilityinjointedrockmasses

WANG Wen,ZHU Wei-shen,CHEN Yun-juan,ZHANG Lei

(GeotechnicalandStructuralEngineeringResearchCenter,ShandongUniversity,Jinan250061,China)

The mechanical behaviors of the jointed rock masses of the roadway were simulated using discontinuous deformation analysis(DDA).Two improvements were developed,which respectively the anchor plastic simulation and improved SSOR-PCG method were implemented into the original DDA program and the advanced program was justified through the comparison with experimental data.Then,the process of damage of the surrounding rocks of the roadway was simulated using the advanced program and supporting method was optimized.At the last,the displacement monitor results of the key points were studied and applied to investigate the optimal support pattern of the roadway,which showed the anchor length with 3 m and the prestressing with 120kN was the optimal support method.

jointed rock masses;surronding rock stability;DDA(discontinuous deformation analysis);anchorage effect;crack propagation

10.13225/j.cnki.jccs.2013.0183

國家自然科學基金重點資助項目(41072234)

王 文(1982—)，女，山東濟寧人，博士研究生。E-mail：sddxww@126.com。通訊作者：朱維申(1932—)，男，教授，博士，博士生導師。E-mail：zhuw@sdu.edu.cn

TD322.4

A

0253-9993(2014)01-0057-07

王 文，朱維申，陳云娟，等.節理巖體巷道的穩定性分析[J].煤炭學報,2014,39(1):57-63.

Wang Wen,Zhu Weishen,Chen Yunjuan,et al.Analysis of roadway stability in jointed rock masses[J].Journal of China Coal Society,2014,39(1):57-63.doi:10.13225/j.cnki.jccs.2013.0183