亥姆霍茲旋轉木馬的實驗研究
呂家琪,牛孔貞,李訓譜
(南開大學 物理科學學院,天津 300071)
1 引 言
約150年前,亥姆霍茲(Hermann Ludwig Ferdinand von Helmholtz)為了測量聲音的頻率,創造了歷史上第一個聲音“頻譜分析器”——亥姆霍茲共振器[1],實現了對于聲音頻率的測定. 在其后的很長一段時間里亥姆霍茲共振器一直是放大、擴聲、吸聲而且不用電子技術的設備[2]. 隨著理論與技術的發展,如今亥姆霍茲共振器在樂器制造、噪聲控制[3]、工業技術優化[4]等方面依然發揮著重大作用. 亥姆霍茲旋轉木馬就是在其共振過程中產生的一個有趣的聲-動能轉化現象.
2 實驗原理
2.1 亥姆霍茲共振器共振原理
所謂亥姆霍茲共振簡言之就是空腔內的氣體共振現象. 圖1為亥姆霍茲共振器早期作為測定頻率的裝置的圖片. 當向空腔口吹氣時,在適當情況下會發出較大的嗡嗡聲,這就是亥姆霍茲共振現象. 當在共振器的口部施加空氣壓力時,共振器內的氣體將被壓縮,假設口部氣體體積不改變,只是空腔內的空氣體積被壓縮,由于聲音的波長遠大于共振器的尺寸,故可以簡化成為彈簧振子模型. 此時腔內氣體就相當于被壓縮的彈簧,腔頸氣體相當于振子,當撤去外界施壓后,彈簧將彈起,而此時的腔頸內氣體將向共振器外射出. 當膨脹過程到達極限時,由于分子之間的作用力,排出的氣體又會回到共振器內,周而復始,便產生振動. 根據經驗公式,依據環境條件和共振器的性質參量計算出共振器的共振頻率為
其中Le=L+1.5r,v為聲速,A為腔口橫截面積,r為腔口橫截面半徑,L為腔頸長度,V為空腔體積[5].

圖1 亥姆霍茲共振器
2.2 亥姆霍茲旋轉木馬的運動機理
亥姆霍茲旋轉木馬的基本結構是將2個相同的亥姆霍茲共振器反向對稱固定于長度、重量適宜的桿的兩端,并在桿的中間位置用細的針頂起或是用細繩懸掛. 當外加的聲音與亥姆霍茲共振器的共振頻率相同時,便會產生共振,即相當于共振器內的氣體被施加以周期性外力. 根據亥姆霍茲共振器原理,當氣體壓縮達到極限后,氣體將如彈簧產生反彈,部分氣體被排出. 氣體排出裝置,腔內氣體將變稀薄,當到達極限時,氣體又會由于分子間的作用力返回到空腔內. 由于空氣分子的平均間距在10-9m的量級,此時氣體分子與氣體分子之間、氣體分子與空腔壁之間的引力很小,故在此彈簧模型中彈簧的壓縮反彈過程比膨脹恢復過程提供動力的效果更明顯,故可認為整個裝置總體上向外排氣. 根據火箭運動原理,裝置將會沿著腔頸口指向腔底的方向轉動.
3 實驗過程
3.1 亥姆霍茲旋轉木馬實驗裝置設計
實驗裝置如圖2所示,亥姆霍茲共振器是飲料瓶,用帶底座的針頭作為旋轉支點,以輕質木條作為旋轉臂. 聲音通過外放音箱提供,實驗數據通過錄像之后對視頻文件逐幀測量來得到.

圖2 亥姆霍茲旋轉木馬實驗裝置
3.2 共振頻率確定實驗
以2.5 L可樂瓶為例,得到其共振頻率的方法是:在飲料瓶口吹氣,當聽到較大的嗡嗡聲即共振時,用錄音筆錄下產生的聲音信號,并對其進行頻譜分析,得到頻譜圖如圖3所示. 在譜線上可以找到幾個明顯的峰值頻率 :93.75,187.50,281.20,359.30,484.30,671.80 Hz. 接下來在其他條件(響度、波形)相同的情況下,分別以這些頻率為聲音信號施加在亥姆霍茲旋轉木馬上,觀察現象,看在什么頻率下裝置才會轉動.
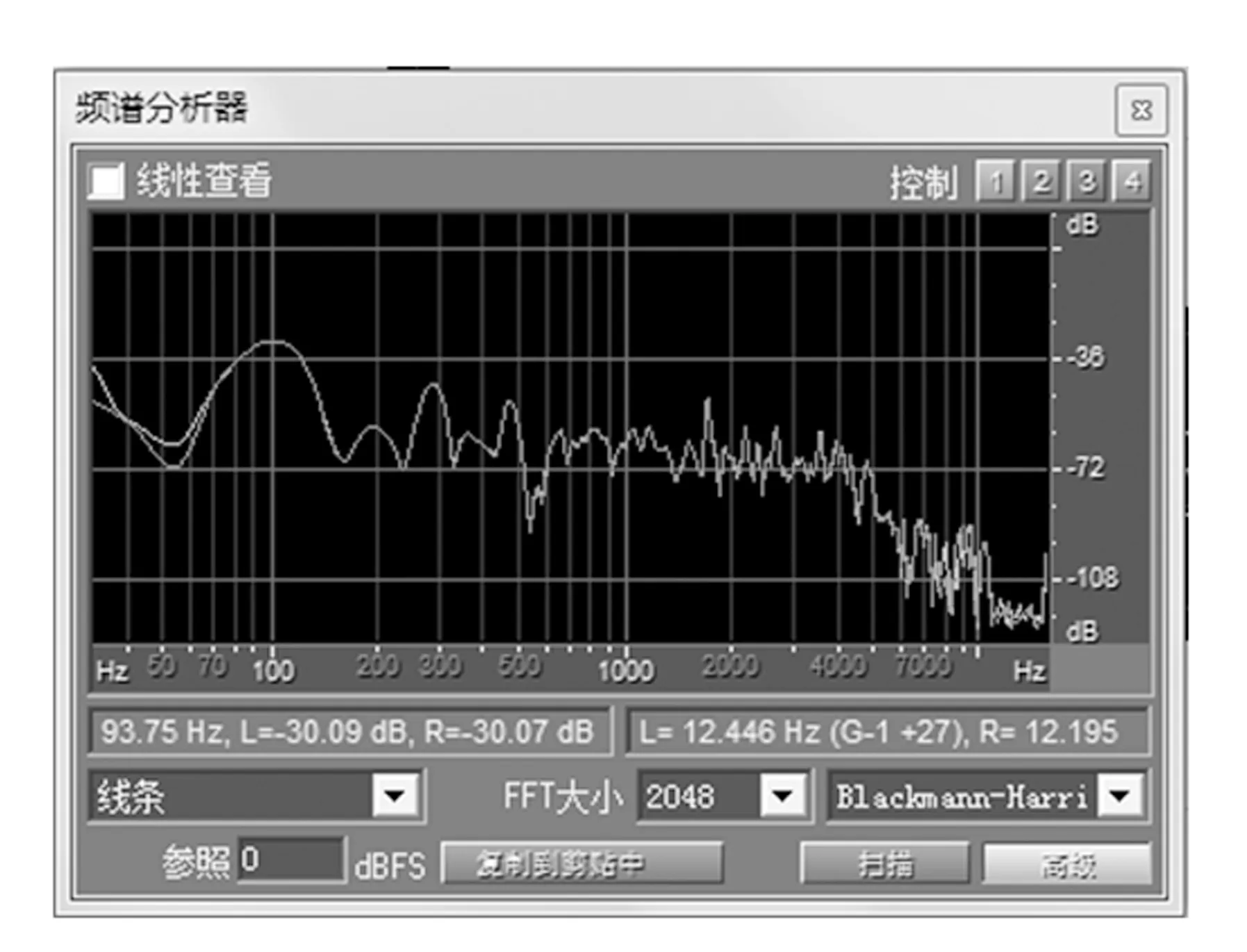
圖3 聲音頻譜圖
實驗表明,只有頻率在93.75 Hz時,裝置才產生轉動. 但是由于在頻譜線上的取值并不很精確,于是在控制其他條件(響度、波形)不變的情況下在93.75 Hz周圍每隔0.25 Hz取1個點,從93.25 Hz取到95.00 Hz,測其周圍頻率點的轉動快慢. 當裝置每轉過弧度π時記錄1次時間,根據時間與轉過角度的關系計算角加速度進而比較快慢. 在其他條件相同的情況下,不同頻率下轉過的角度與時間關系的實驗數據如表1所示.
根據表1做出不同頻率下的θ-t曲線,并做多項式擬合. 以角加速度最大的93.75 Hz為例,θ-t
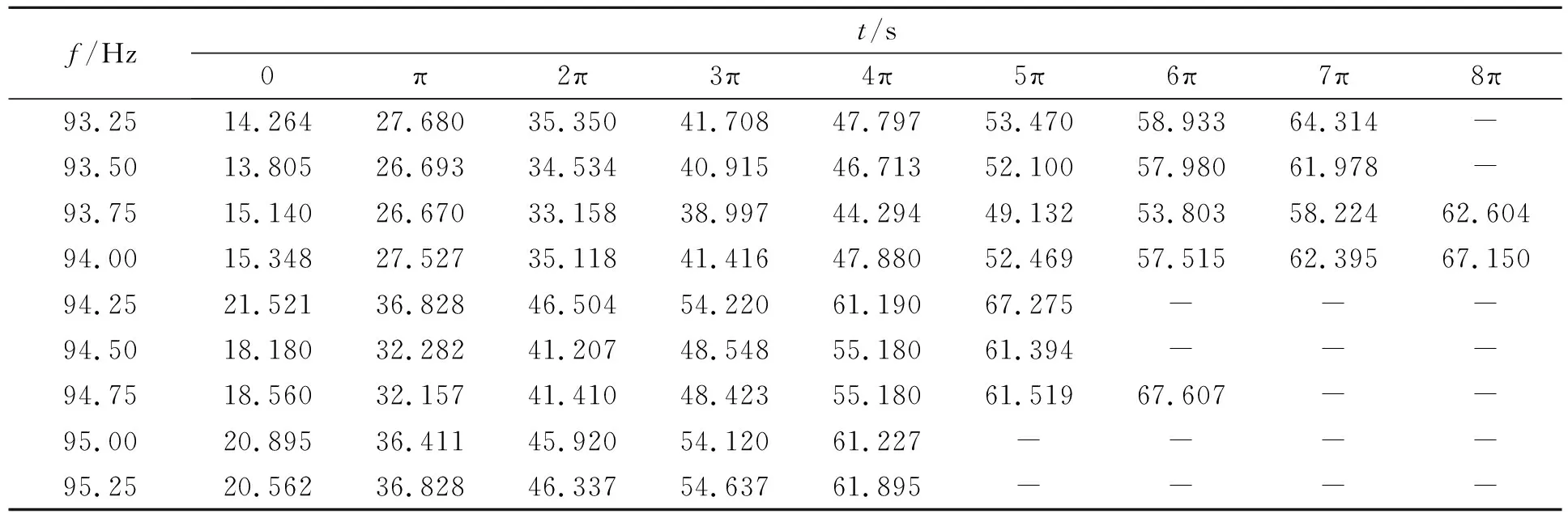
表1 不同頻率下轉過的角度與時間關系的實驗數據
曲線見圖4,θ=0.006 0t2+0.07t-2.4,R=0.998 98,發現其為擬合度很高的勻加速運動關系. 根據得出的擬合方程,可以計算出不同頻率下的角加速度. 將角加速度和頻率的關系做出曲線如圖5所示,并與實驗所用的93.75Hz的聲音信號頻譜圖像(如圖6)作對比,發現兩者形態基本相同. 由此可得2.5 L可樂瓶作為亥姆霍茲共振器的實際共振頻率即為單頻93.75 Hz.

圖4 θ-t曲線
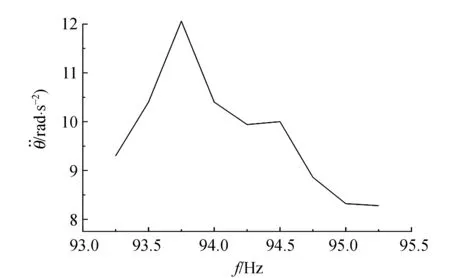
圖曲線
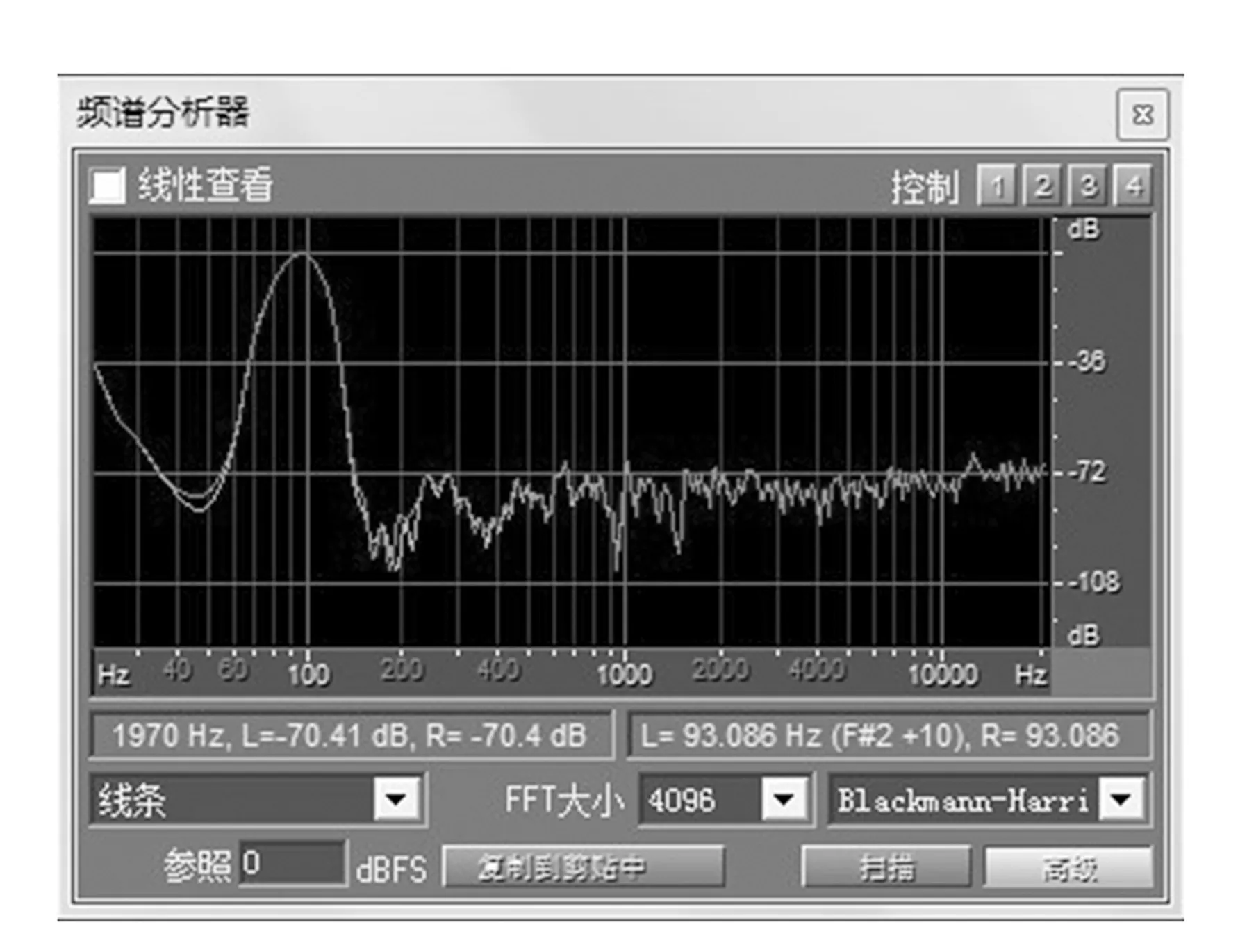
圖6 93.75 Hz聲音信號頻譜圖
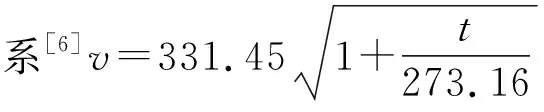
3.3 長時間運動最終狀態
亥姆霍茲旋轉木馬的轉動從能量角度來看是聲波振動的能量轉化為了裝置的轉動動能. 由于聲源穩定,能量必存在上限值,裝置在長時間的情況下不可能一直進行勻加速運動,而會逐漸到達穩定狀態. 基于這樣的考慮,把實驗時間擴展到5 min(93.75 Hz,正弦波,響度固定),并觀察其現象. 結果發現裝置先是加速運動(如圖A段),其后一段時間速度穩定為勻速(B段),到120 s以后開始減速(C段),并在169 s時停止運動. 為了與能量建立更直接的關系,取轉動路程為縱坐標,運動時間為橫坐標,記錄數據,做出運動時間與路程關系圖(L-t圖),如圖7所示. 然后通過觀察加速度變化分析運動過程.
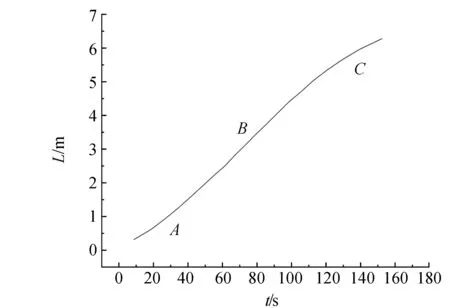
圖7 L-t關系圖
這一過程與理論分析相吻合:氣體向外排出是主要過程,而氣體吸入則是次要過程. 這也就是說氣體排出的量要大于氣體的吸入量,氣體要不斷流失,這既是裝置得以運動的原因,又是裝置最終會靜止的原因. 由于腔內氣體整體上呈排出狀態,根據動量守恒定律裝置將會沿遠離腔口的方向運動. 同時腔內氣體在運動過程中將逐漸稀薄,此時撞向瓶底獲得反向速度的氣體分子數也將越來越少,排氣過程逐漸減弱,排氣量和排氣速度都不斷降低,最終由于存在外界阻力,裝置將變為勻速運動進而變為減速運動直至靜止. 在裝置運動過程中,當把手放在腔口時也能感受到3個不同階段排出裝置的氣流強度逐漸減弱的變化.
3.4 波形影響實驗
就不同波形對亥姆霍茲旋轉木馬轉動角加速度的影響做了研究. 在其他條件不變的情況下改變外加聲音的波形,觀察并測量、計算裝置轉動的角加速度. 采用的波形有:正弦波、半正弦波、三角波、方波,得出了波形為方波時裝置轉動的角加速度明顯最大的結論(數據和實驗曲線從略). 這一現象可以從能量角度加以分析:由方波的傅里葉展開可知,方波在其基頻上的展開系數相比其他幾種波形要大[7],也就是說聲能量更大,又由于本實驗裝置是依靠單一共振頻率驅動,所以方波對共振時的能量輸入更多. 故在其他條件相同的情況下,方波信號驅動下裝置轉動的角加速度明顯最大.
4 結束語
通過用自行設計的簡易實驗裝置對亥姆霍茲旋轉木馬的聲-動能轉化現象進行觀察、分析和討論,加深了對這一有趣物理現象的認識和理解,進一步感受到物理世界的奧妙,激發了對物理學習的興趣. 通過本實驗所測定的共振器共振頻率與用理論公式計算得到的結果基本相符,說明了用比較角加速度大小的方法研究亥姆霍茲旋轉木馬是一種簡便可行的方法. 本實驗還對旋轉的全過程及波形對轉動快慢的影響進行了有益探索.
參考文獻:
[1] 馬大猷. 亥姆霍茲共鳴器的發展[J]. 物理,1993(8):452-456.
[2] 馬大猷. 亥姆霍茲共鳴器[J]. 聲學技術,2002(Z1):1-3.
[3] 晏偉成,景曉東. 基于主動亥姆霍茲共振器的噪聲控制實現[A]. 自動化及先進集成技術大會論文集(二)[C],2007:333-335.
[4] 孔德鵬,李宏楷,劉云磊,等. 基于亥姆霍茲共振腔的香味自動排放裝置設計[J]. 電腦知識與技術,2012(31):7589-7591.
[5] Tom Irvine. Beverage Bottles as Helmholtz Resonators. [EB/OL]. vibrationdata.com. 2004:1-13.
[6] 郭立群,吳波,黃艷芳,等. 聲速隨溫度變化的智能測試研究實驗[J]. 物理實驗,2013,33(6):20-22.
[7] 劉光旭,張效成,賴學堅. 高等數學[M]. 北京:高等教育出版社,2008:308-309.

