基于傅里葉變換的激光數字散斑測量平板玻璃的楔角

譚佐軍，謝 靜

（華中農業大學 理學院 應用物理系，湖北 武漢430070）

1 引 言

激光照射散射體表面產生漫反射或通過透明散射體時，在散射表面或附近光場中觀察到的無規則分布的明暗斑點稱為激光散斑.散斑現象普遍存在于光學成像的過程中，通過對散斑場的分析可以測量物體的一些物理特征值［1］.因此激光散斑計量技術成為現代光學重要的測量方法，主要有：直接照相法、雙曝光法、電子散斑干涉法、錯位散斑干涉法和散斑相關測量技術等.它具有全場、非接觸、高精度、高靈敏度和實時快速等優點［2］，現已廣泛應用于振動、位移、形變、斷裂、粗糙度的測量，農業及生物醫學等方面.因此激光散斑成像技術成為很多學校在教學實驗中推廣的一個實驗，該實驗的引入有利于學生了解激光散斑的特性及其在各個領域中的應用［3-4］.

平板玻璃是一種拋光后的相位物體，其表面光滑，不能產生激光散斑，因此無法直接利用激光散斑技術測量其微小楔角.我們在光路中借助能夠產生激光散斑的元件（毛玻璃等），采用傅里葉變換的數字激光散斑技術測量了平板玻璃的微小楔角.該方法直觀、快速、精度高，有利于學生了解激光光束的基本特點以及CCD光電成像系統的原理，通過實驗學生還可以進一步鞏固光的衍射、光的干涉、激光高斯光束特性、信息光學等相關知識.該方法也可以引導學生開拓思路，從而利用激光散斑技術對拋光物體進行位移和旋轉等測量.

2 測量原理

基于傅里葉變換的數字激光散斑技術測量平板玻璃微小楔角的光路如圖1所示.圖1中M為毛玻璃，CCD放置于H處為記錄激光散斑，W為帶有微小楔角的平板玻璃.

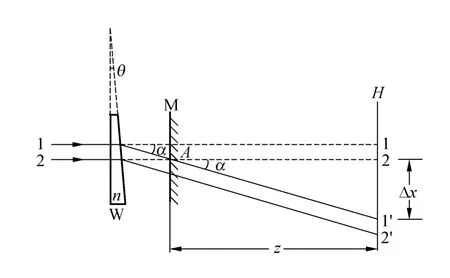
圖1 數字散斑技術測量平板玻璃楔角光路示意圖

當平板玻璃W不在光路中時，激光束將直接照射毛玻璃，毛玻璃作為透明的散射體在其附近的光場中產生激光散斑.當把平板玻璃W放入光路中，由于微小楔角的作用，經過平板玻璃W出射后的光線將偏移α角度，假設光線1通過毛玻璃上的A點，而沒有平板玻璃時光線2通過A點，這就意味著在沒有平板玻璃W時，A點產生的散斑在位置2，加入平板玻璃后，A點產生的散斑就移動到1′處，位置2和位置1′間距為Δx，這就是1對散斑.因此H處的CCD就可以記錄形成的散斑場.根據圖1的幾何關系，散斑位移量Δx和平板玻璃楔角θ的關系為［5］

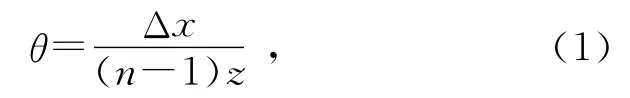
式中z為毛玻璃到CCD之間的距離，n為玻璃折射率.

光路未加平板玻璃和加入平板玻璃2次記錄的激光散斑強度分布完全相同，但是兩者有相對位移x0，設未加平板玻璃CCD像面上散斑強度分布為A0（x0，y0），加入平板玻璃位移后的強度分布為AL（x0-Δx，y0），則2個散斑圖疊加的光強可表示為

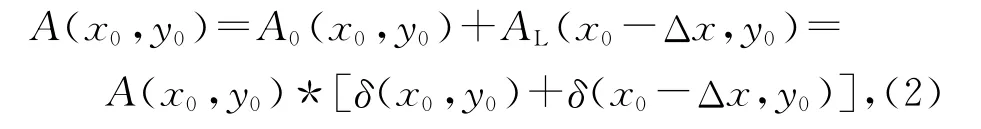
式（2）中＊表示卷積.對相加的散斑圖進行傅里葉變換可得其頻譜分布為［6-7］

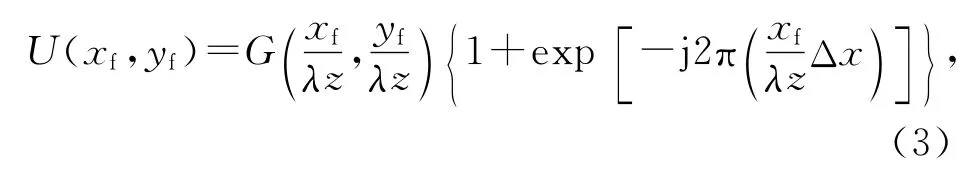
式（3）中λ為光波波長.光強分布可表示為

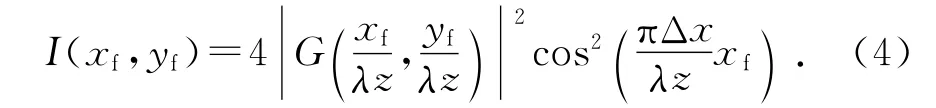
可見，在頻譜面上觀察到的光強分布是有散斑結構的楊氏雙縫干涉條紋，條紋間距為

根據式（1）和式（5）可以得平板玻璃楔角的計算公式為

3 實驗研究

3.1 散斑圖像獲取

按圖1所示光路進行實驗，系統中光源采用He-Ne激光器，波長為632.8nm，用1對偏振片進行光強調節.CCD采用AVT相機STINGAY系列F504B／C，該CCD分辨率為2 452×2 052像素，像元尺寸為3.45μm×3.45μm.首先在未放入平板玻璃時，用CCD采集激光束照射毛玻璃產生的散斑圖，如圖2（a）所示，然后放入平板玻璃，用CCD采集此時的散斑圖，如圖2（b）所示.

圖2 CCD采集的激光散斑圖

3.2 干涉條紋獲取及分析

根據式（2）～（4）分析，在 Matlab中將圖2中的圖（a）和圖（b）相加，相加后的結果進行快速傅里葉變換，可得頻譜面上的光強分布，圖3非常清晰地展現了有散斑結構的楊氏雙縫干涉條紋.這也說明采用大圖像高分辨率的CCD可以提高相關條紋場的信噪比［8］，降低了條紋處理的難度.

用與條紋圖像維度相同的一維全1矩陣可抽取條紋圖像x方向的光強分布圖，如圖4所示.由圖4（a）可見，盡管獲取了信噪比比較高的散斑楊氏雙縫干涉條紋，但是仍然存在噪聲的影響，曲線顯出很多毛刺，這導致光強分布曲線出現不確定的極值點，不消除這些噪聲就無法準確計算條紋間距.因此采用移動平均法對曲線進平滑處理，在此采用20pixel大小的移動窗口，處理結果如圖4（b）所示.從圖4（b）可見，平滑后的條紋分布曲線消除了條紋上毛刺，同時保證了條紋中心像素的位置不變.

圖3 快速傅里葉變換獲得的楊氏雙縫干涉條紋

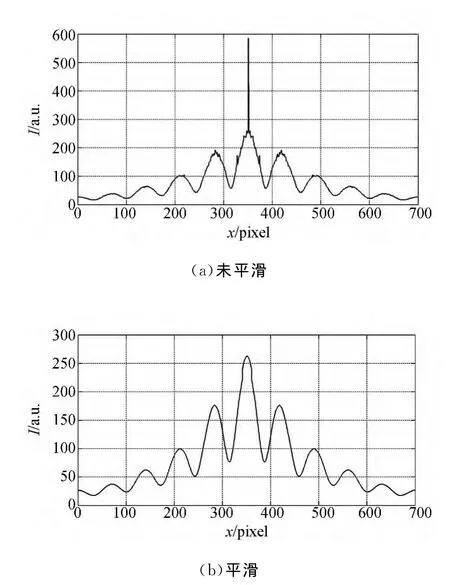
圖4 光強分布曲線

3.3 干涉條紋間距的計算

用CCD記錄散斑圖，通過FFT獲取干涉條紋，由于CCD成像系統及圖像處理等因素導致存在系統傳遞函數，必須進行像素單位與實際尺寸之間的度量單位轉換［9］.測得條紋間距為l′與實際的條紋間距l的關系為

式（7）中b是系統誤差，通過2次標定就可以確定k和b.選用定標板，通過CCD成像系統，測得Y1占有的像元數N1，測得Y2占有的像元數N2，將Y1，Y2，N1，N2代入式（7），可得

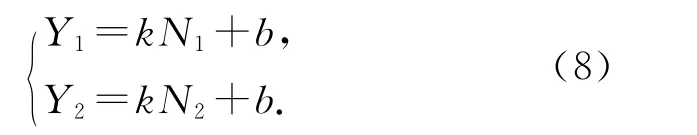
4 實驗結果及分析

在實驗中分別用自準直法和激光數字散斑法對同1塊平板玻璃進行重復測量.環境為室溫，當CCD接通電源后約15min開始測量，以便CCD達到穩定的工作狀態.表1為測試結果，l＝（2.966±0.003）mm，θ散斑＝1.420 6′±0.001 5′，θ自準直＝1.416′±0.017′.

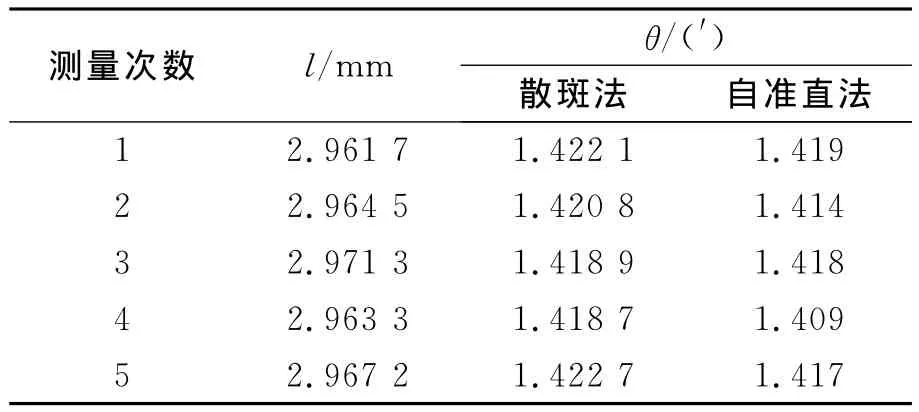
表1 測試數據

利用定標板中的1mm和2mm刻線確定k＝0.043 5mm／pixel，激光數字散斑法系統誤差b＝0.001 2mm，激光器波長為632.8nm，平板玻璃折射率n＝1.516.作為5次重復測量的物理量，同時為了保證標準不確定度的置信水平，把平均值的標準偏差乘以t0.95（1.96）因子作為測量結果不確定度的A類分量，為了便于教學，將儀器誤差按均勻分布近似處理，把自準直儀器誤差除以作為自準直法的B類分量，自準直儀測量誤差為1″.由表1可見，基于FFT的激光數字散斑法測量的結果與自準直法測量結果吻合較好，效果非常理想.

5 結束語

本文用傅里葉變換激光數字散斑圖測量了平板玻璃的微小楔角.該方法測量參量少、光路簡單、精度高、實驗現象直觀、效果好、實驗操作簡單，適合本科生的實驗教學.學生可以從實驗中進一步鞏固光的衍射、光的干涉、激光高斯光束特性、信息光學等相關知識，加深了學生對激光散斑的成像原理以及應用理解.該方法也可引導學生開拓思路，利用激光散斑技術對拋光物體進行位移和旋轉等測量.該實驗可以激發學生的興趣，促進學生向研究性學習和創新性學習的轉變.

［1］Dainty J C.Laser speckle and related phenomena［M］.Berlin and New York：Springer-Verlag，1975.

［2］Sj¨odahl M.Electronic speckle photography：increased accuracy by nonintegral pixel shifting［J］.Appl.Opt.，1994，33（28）：6667-6673.

［3］王中平，張權，朱玲，等.CCD成像輔助激光散斑實驗［J］.物理實驗，2010，30（10）：11-14.

［4］黃水平，張飛雁.激光散斑在大學物理實驗教學中的應用［J］.物理與工程，2011，21（1）：37-39.

［5］肖明海，王幗華.平板玻璃微小楔角的散斑法測量［J］.激光技術，1989，13（1）：42-45.

［6］呂乃光.傅里葉光學［M］.北京：機械工業出版社，2006：1-50.

［7］姚琨，陳蝶萍，張權，等.頻譜法在光的雙縫干涉計算中的應用［J］.南京氣象學院學報，2000，23（3）：445-448.

［8］李喜德，伍小平.用快速傅里葉變換實現雙曝光散斑場的全場信息再現［J］.光子學報，1996，25（3）：261-265.

［9］俞曉磊，趙志敏，郭林峰.激光散斑干涉條紋的CCD分析技術研究［J］.應用激光，2007，27（5）：378-381.