用傅里葉定律分析無限大平行平板中的準穩(wěn)態(tài)
羅 宏
(蘇州科技學院 數(shù)理學院,江蘇 蘇州 215009)
1 引 言
準穩(wěn)態(tài)法測量材料的熱物性是一種較精確的動態(tài)測量方法,在各類固、液以及納米材料的熱物性測量中得到了應用[1-4]. 其特點是效率高,所得數(shù)據(jù)較多. 準穩(wěn)態(tài)實驗作為測量比熱容和導熱系數(shù)的方法也引入了大學物理實驗教學中[5-6],作為一種應用動態(tài)方法的實驗,開闊了學生的思路和視野.
2 無限大平行平板中準穩(wěn)態(tài)分析
在實驗中常采用第二類邊界條件下的無限大平板模型作為準穩(wěn)態(tài)實驗的基礎[1,3-5]. 導熱系數(shù)及比熱容的計算式由平板的溫度分布函數(shù)導出[5,7]. 進一步了解溫度分布函數(shù)的推導過程則涉及到解第二類邊界條件下的熱傳導微分方程:
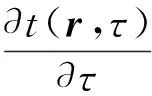
(1)
用到分離變量法,以及傅里葉分析等[8].
將以上方法應用到實驗教學中,存在2個問題,其一是對大部分學生而言理論基礎要求過高,其二是公式的推導過程并沒有幫助學生了解準穩(wěn)態(tài)是怎樣的物理過程及其特點.
本文根據(jù)一維情況下的傅里葉定律
(2)
結合比熱容的定義
dQ=cmdt,
(3)
分析了實驗系統(tǒng)中的準穩(wěn)態(tài)物理過程及其物理特征,并推出導熱系數(shù)的計算公式,得到了與解偏微分方程一致的結果.
如圖1所示,無限大各向同性的均勻平行平板厚度為d,一個表面絕熱,另一個表面的熱流密度-qc為常量,此處負號是考慮其方向為負. 假設平板的導熱系數(shù)λ、比熱容c和密度ρ不隨溫度變化. 建立如圖1所示坐標,使x軸垂直于平行平面,原點位于絕熱表面上.
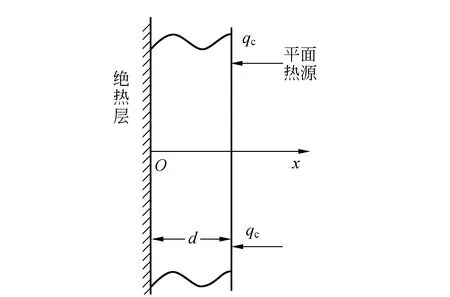
圖1 恒熱流密度下的無限大平行平板
由系統(tǒng)的對稱性知,熱流密度必然與x軸平行,并且x相同的位置,熱流密度相同,熱流密度是x的一維函數(shù). 平板被持續(xù)加熱,其溫度必然不斷升高. 但由于流入的熱流密度始終為常量,可以合理猜想流入的熱量被平板各處均勻吸收. 當然這是經(jīng)過初始過渡過程之后,達到“穩(wěn)定”的狀態(tài),即準穩(wěn)態(tài)時的情況. 由以上分析,假設平板中的熱流密度為
q=ax+b,
(4)
以下由微元法,通過物理過程說明這正是系統(tǒng)“穩(wěn)定”后的狀況,并求出常量a,b.
將平板沿平行于表面的方向分為無窮多個等厚的薄層,薄層厚度Δx趨向于無窮小. 任取相鄰的2個薄層Vi+1,Vi+2,如圖2所示. 圖中所示熱流密度為箭頭所指面上所流過的熱流密度. 因薄層為任取,以下的討論具有普遍性.
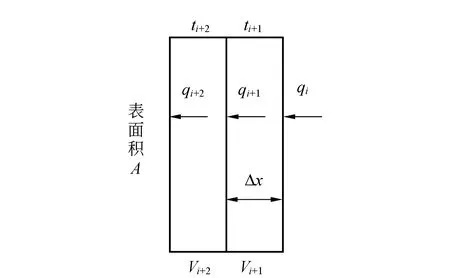
圖2 平板中的2個薄層微元
研究Vi+1,由熱容式(3)及能量守恒知,時間dτ內(nèi),流入流出的熱量差等于溫度變化而吸收的熱量
ΔQ=(qi-qi+1)Adτ=cΔmdti+1,
(5)
由Δm=ρAΔx(ρ為板的密度),式(5)變?yōu)?/p>
(6)
當Δx趨向于無窮小,等式左端即熱流密度的導數(shù)dq/dx. (6)式以及(2)式描述了熱量在板內(nèi)流動、吸收的情況,限定了熱流密度和溫度的關系,是熱流密度和溫度必須滿足的等式.
以下類比力學中穩(wěn)定平衡的概念,通過說明(4)式所代表的狀態(tài)是平衡且穩(wěn)定的,來說明這種狀態(tài)會自發(fā)、持續(xù)存在.
首先說明(4)式代表“平衡”的狀態(tài),即可以持續(xù)存在的狀態(tài). 由(6)式可看出,等式左側熱流密度對空間的導數(shù)處處為常量時[熱流密度為空間的線性函數(shù),即(4)式],等式右側所有薄層中溫度對時間導數(shù)為常量. 當各處溫度的時間導數(shù)為常量時,其空間梯度必為時不變函數(shù),則由(2)式,要求熱流密度為時不變函數(shù). (4)式滿足這一要求. 同時也要求外加熱流密度為常量,這正是假設的條件. 由此(4)式滿足了(2)和(6)式,同時是時不變的狀態(tài),可以持續(xù)存在. 此時,熱流密度線性變化,各薄層吸熱速率相同,導致溫升速率相同. 相同的溫升速率說明溫度梯度不隨時間變化,又保證了此熱流密度不發(fā)生改變,狀態(tài)持續(xù)存在. 溫升速率相同,是準穩(wěn)態(tài)的特征,此狀態(tài)為準穩(wěn)態(tài).
接下來,說明其是“穩(wěn)定平衡”,也就是如果系統(tǒng)不在此狀態(tài),會自發(fā)地向此狀態(tài)演化. 需要考慮2個相鄰的薄層,分析熱流密度偏離上述狀態(tài)之后,系統(tǒng)如何自我調(diào)節(jié). 如果qi-qi+1>qi+1-qi+2,則由(6)式知ti+1升高的速率大于ti+2,導致兩薄層間的溫度差加大,由(2)式知qi+1將增大,其結果是qi-qi+1減小,qi+1-qi+2增大,上面不等式兩端的差距縮小. 若qi-qi+1 由以上文中分析可以得出,無限大平行平板系統(tǒng)趨向且穩(wěn)定于熱流密度隨x線性變化的狀態(tài). 此時,所有部分溫升速率相同,這正是準穩(wěn)態(tài)的特征. 根據(jù)邊界條件及(4)式,q(0)=b=0,q(d)=-qc=ad,則b=0,a=-qc/d,代入(4)式得: (7) 將(7)式代入傅里葉定律(2)式, (8) 將上式從0到x積分,得到x處溫度 (9) 可見溫度場為拋物線函數(shù). 若x=d,則可得 (10) 式中Δt=t(d)-t(0),為平板2個表面的溫度差,上面已經(jīng)說明,其為常量. 此式為準穩(wěn)態(tài)下,利用無限大平行平板測量導熱系數(shù)的計算公式. (9)和(10)兩式與用熱傳導微分方程(1)推導出的結果相同[7],驗證了結果正確. 準穩(wěn)態(tài)下的平行平板問題在熱物性參量的測量中常被用到. 本文從熱流密度著手,這正是從準穩(wěn)態(tài)的特點出發(fā). 準穩(wěn)態(tài)的特點是物體中所有點的溫升速率都相等,由傅里葉定律知,這就導致空間中的熱流密度不隨時間變化. 從不變量著手可以更容易地解決問題,所以從熱流密度著手有其合理性. 熱傳導微分方程(1)式本身就是建立在傅里葉定律和比熱容定義式基礎之上. 所以本文的方法和傳統(tǒng)的方法有相同的基礎. 只是本文的方法更強調(diào)物理的概念和過程. 相對于解偏微分方程的方法,更簡單易懂,利于教學. 學生反復應用物理的概念、分析物理過程,有利于學生熟悉物理概念、建立物理直覺. 參考文獻: [1] 周樂平,王補宣. 準穩(wěn)態(tài)法測量納米顆粒懸浮液的熱物性[J]. 工程熱物理學報,2003,24(6):1038-1039. [2] 何茂剛,鐘秋,薛榕,等. 變?nèi)莘e量熱器法測量液體比熱容研究[J]. 熱科學與技術,2008,7(1):70-74. [3] 周孑民,曾文輝,葉良春,等. 有機玻璃熱物性準穩(wěn)態(tài)法實驗研究[J]. 工業(yè)計量,2005,15(6):10-12. [4] 盧建航,孫宏,尹海山. 用準穩(wěn)態(tài)法測定橡膠及橡膠基復合材料的導熱系數(shù)和比熱容[J]. 輪胎工業(yè),2001,12(5):305-309. [5] 趙海發(fā),劉世剛,金恩培,等. 新型準穩(wěn)態(tài)法不良導體熱物性參數(shù)測定儀的原理與應用研究[A]. 全國高等學校物理基礎課程教育學術研討會[C]. 2008:400-402. [6] 張紅佳,郭永利,李正,等. 真空熱流法測定不良導體的導熱系數(shù)[J]. 物理實驗,2012,32(9): 5-7. [7] 郭重雄,余其錚,薛洪福. 導熱系數(shù)和比熱準穩(wěn)態(tài)測量方法的分析[J]. 哈爾濱工業(yè)大學學報,1984(2):62-72. [8] 雷柯夫 A B. 熱傳導理論[M]. 裘烈鈞,丁履得,譯. 北京:高等教育出版社,1955:155-157.3 結束語

