物理學中的絕熱不變量及實驗設計
李岸陽,王雨雷,魏雅利
(1.中核清原環境技術工程有限責任公司,北京 100037;2.中國科學技術大學 近代物理系,安徽 合肥 230026; 3.北京市5111信箱,北京 100094)
1 引 言
絕熱不變量是近代物理學中的重要概念. 其產生背景可追溯到1911年索爾維(Solvay)會議[1]. 當時在討論量子力學問題期間,洛侖茲提出了一個看似簡單的問題,即當單擺的周期緩慢變化時,其振幅如何變化. 愛因斯坦第一個回答了這個問題,并提出了絕熱不變量概念.
簡諧振子等周期問題是物理學中少有的幾個能夠被嚴格解析解決的問題. 然而,真實世界中,嚴格的周期系統并不存在. 大部分我們熟知的周期系統,如行星公轉、水波傳播、心率等都不嚴格. 它們實際是具有近似周期行為的準周期系統. 在研究準周期系統時,一方面周期的嚴格定義需要重新被考慮,如何準確描述準周期系統的長時間演化成為一個極富實踐意義的問題. 另一方面,在周期性系統中存在的守恒量在準周期系統中并不嚴格成立,這大大增加了對準周期系統進行研究的難度. 絕熱不變量的提出使我們找到了準周期系統中相對應的“守恒量”,具有重要意義. 在許多情況下,絕熱不變量并不被廣泛認識,絕熱不變量和近似不變量之間經常被混淆.
總的來說絕熱不變量與近似不變量的差別在于物理量在長時間時的性質. 由于準周期系統的參量一般都隨時間緩慢變化,因此許多相應物理量也隨時間緩慢變化,在很長時間后由于不斷積累,該物理量會變化很大,這就是近似不變量的概念. 而絕熱不變量在短時間內變化可能和近似不變量同一量級,但經過很長時間后,絕熱不變量的變化仍然很小.
本文擬從絕熱不變量的定義出發,詳細闡釋其性質與重要意義. 通過設計簡單的準周期系統物理實驗,可以測定系統中的絕熱不變量,從而加深對絕熱不變量性質的理解.
2 準周期系統中的絕熱不變量
周期系統不變量的研究在物理領域有著基本的意義. 幾乎所有的系統都可以轉化為周期系統進行考慮,如通過傅里葉變換等方法將一個復雜的函數分解為不同周期性的正弦函數,從頻域角度分析問題. 周期系統不變量反映了系統的對稱性,這不僅可以簡化物理問題,而且能夠幫助人們抓住問題的物理本質,加深對相關系統的理解.
理想諧振子為周期系統,其哈密頓量為[2]
(1)
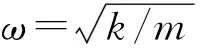
p=mωqcotQ,
(2)
(3)
方程(1)形式上變為
H=ωP.
(4)
由于H不顯函Q,變換后的動量,P=H/ω,為守恒量. 這個守恒量不僅揭示了理想諧振子系統的本質屬性,而且它可以很自然的推廣到其他的大部分周期系統中. 因此守恒量的意義可見一斑.
周期系統具有嚴格固定的頻率及相應的守恒量,然而實際的物理問題中,理想的周期系統是不存在的. 對于非周期系統,宏觀意義上的“頻率”、“相位”等概念都變得模糊不清,大部分系統只能從微觀意義上定義“瞬時頻率”. 為了簡化問題,考慮瞬時頻率隨時間演化相對極慢的系統,即
(5)
其中,ω(t)為系統瞬時頻率. 這種系統稱為絕熱系統,其隨時間的演化就是絕熱演化過程. 從物理意義上來說,絕熱系統比周期系統更貼近物理實在,因此,此系統守恒量的研究也就極為重要. 絕大多數絕熱系統存在3種不變量:守恒量、近似不變量和絕熱不變量. 守恒量就是嚴格不含時的物理量,然而,近似不變量和絕熱不變量很容易混淆,他們的區別就是長時間性質不同.
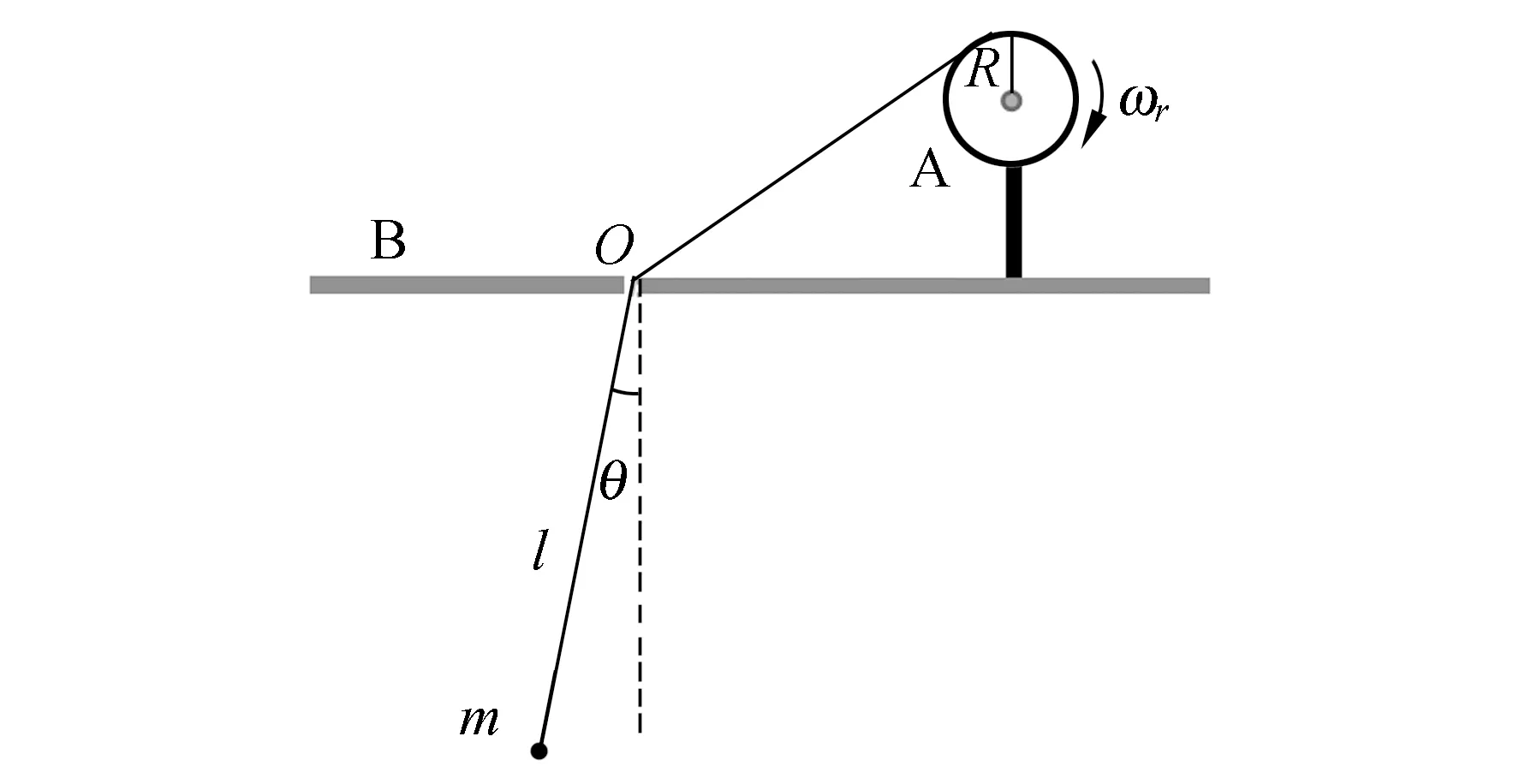
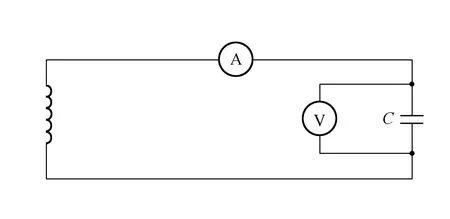
近似不變量定義為:在時間區間0 (6) 其中,ω(t)滿足式(5). 定義物理量 (7) 其中,參量s>0,ps(t)和qs(t)滿足方程 (8) 方程(8)實際就是以t=s時刻的ω(s)為固定頻率的哈密頓量,方程(7)則定義了瞬時周期和相應的作用量. Arnold證明,如果0 絕熱不變量的定義與近似不變量相似,但是絕熱不變量沒有時間上的限制,即對任意時刻t,如果物理量A(t)的增量ΔA=A(t)-A(0)~O(ε),則該物理量就是絕熱不變量[4]. 近似不變量與絕熱不變量的性質可以通過圖1來定性說明. 圖1中A1為近似不變量,A2為絕熱不變量,經過長時間后,A1變化可能很大,而A2與t=0時刻相差仍為一階小量. 圖1 近似不變量與絕熱不變量的對比 單擺是物理學中的非常簡單的問題,在物理實驗和教學領域,單擺被廣泛關注[5-7]. 但如果單擺的擺長隨時間改變,那么系統運動的求解就變得很復雜[1]. 如果單擺的擺長絕熱演化,單擺就變成了絕熱系統,在該系統中存在絕熱不變量. 變擺長單擺實驗裝置如圖 2所示. 擺長為l,牽引裝置A的轉盤半徑為R,角速度為ωr,要求ωr滿足絕熱條件 (9) 擺線與木板B的孔O的摩擦可以忽略,小孔經過拋光、潤滑等處理,θ為擺線與垂直線的夾角,為了保證單擺條件,要求整個過程中θ<10°,由于擺幅與轉盤速度相關,因此,實驗中可以通過人為調整轉速來達到單擺條件. 圖2 變擺長單擺實驗裝置示意圖 固定擺長單擺系統的拉氏量為 (10) 利用拉格朗日方程和單擺條件易得運動方程為 (11) 對于變擺長單擺,方程(11)可寫為 (12) (13) 滿足絕熱條件. 設w(t)為任意含時物理量,w(t)滿足方程 (14) 可以通過方程(12)和(14)得到該變擺長單擺系統的一個守恒量[1, 4], (15) 可以很容易驗證dI/dt=0. 考慮到Ω(t)隨時間變化很慢,可以將其重參量化為Ω=Ω(T),其中T=εt. 方程(14)形式上變為 (16) 令w=u0+εu1+ε2u2+…,逐級求解方程(16),可得[4] w=Ω-1/2+O(ε2), (17) (18) 基于I定義一個新的守恒量 (19) 將(17)式和(18)式代入(19)式,可以得到 (20) (21) 定義物理量 (22) 對比(20)和(22)式易得 Ap=Ip+O(ε), (23) 考慮到Ip為守恒量,因此,在任意t時刻,有 [Ap(t)-Ap(0)]~O(ε), (24) 因此,Ap為變擺長單擺系統的絕熱不變量. 利用圖1所示的裝置,可以通過實驗來驗證Ap為絕熱不變量. 考慮到單擺系統處在保守勢場中,并且廣義坐標p和q不顯函時間,所以哈密頓量為單擺的能量,即H=E. 為了減小測量誤差,可以通過測量最大擺角θmax來得到能量,即 H=E=mgl(1-cosθmax). (25) 設初始時刻擺長為l0,t時刻裝置A轉過的角度為Φ,因此有 l(t)=l0-RΦ. (26) (27) 因此,待測量為Φ(t)和θmax(t),通過測量不同時刻的Ap就可以明確看出Ap的絕熱不變性. 應該注意的是,本實驗要求全過程滿足單擺條件,即θ<10°,對擺長沒有限制. LC回路是電學中簡諧振蕩的重要實例,如圖3所示,為了保證回路能量損失較小,電感L與電容C都比較大, 靈敏電流計的電阻極小, 電 壓表電阻極大. 最簡單的情況下,認為電感與電容不變,這種理想情況下電流i滿足的方程為 (28) (29) 仍然利用方程(14)獲取LC回路的守恒量 圖3 LC回路實驗示意圖 (30) 進一步,利用(16)~(20)的思路,可以得到 (31) 定義物理量 (32) 其中V為電壓表讀數. 利用電感定律V=-Ldi/dt,對比(31)和(32)式容易看出 ALC(t)=I′+O(ε). (33) 考慮I′為守恒量,因此對任意時刻t,ALC(t)滿足 [ALC(t)-ALC(0) ]~O(ε), (34) ALC為絕熱不變量. (35) 通過測量不同時刻ALC,可驗證絕熱不變的性質. 討論了準周期系統中的絕熱不變量. 以變擺長單擺和LC回路2個物理系統為例,分別證明和獲得了相應的絕熱不變量,并提供了實驗上進行測量的思路和方法. 2個例子都是含時諧振子方程的具體表象,大部分物理系統都可以利用含時諧振子方程研究,其絕熱不變量可以反映大多數物理系統的“近似”守恒性質,因此,盡管這2個實例計算絕熱不變量的過程并不復雜,但是,其揭示的物理意義是非常基本和重要的,對于理解復雜物理系統是很有幫助的. 參考文獻: [1] Kulsrud R M. Adiabatic invariant of the harmonic oscillator [J]. Physical Review, 1957,106(2):205. [2] Goldstein H, Poole C, Safko J. 經典力學[M]. 北京:高等教育出版社,2005:377-379. [3] Arnold V I. Mathematical Methods of Classical Mechanics [M]. New York: Springer Press, 1989. [4] Qin H, Davidson R C. An exact magnetic-moment invariant of charged-particle gyromotion [J]. Physical Review Letters, 2006,96(8):085003. [5] 秦鳴雷,肖一凡,楊海亮,等. 大角度下阻尼對單擺擺動周期的影響[J]. 物理實驗,2012,32(5):42-45. [6] 張虹雪,陳雪芹,樊婷,等. 單擺擺球運動軌跡控制裝置[J]. 物理實驗,2013,33(12):36-38. [7] 蔡霞,吳先球. 基于虛擬儀器實現單擺法測量重力加速度[J]. 物理實驗,2012,32(8):28-29.
3 變擺長單擺的絕熱不變量
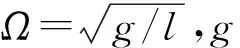
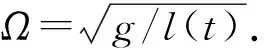

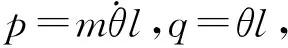
4 變參量LC回路的絕熱不變量
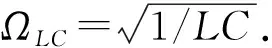
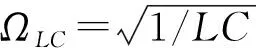
5 結束語

