一類具變指數(shù)源的p-Laplace方程解的爆破時間下界

孟繁慧，高文杰

(1.長春金融高等專科學校，長春 130028;2.吉林大學數(shù)學學院，長春 130012)

一類具變指數(shù)源的p-Laplace方程解的爆破時間下界

孟繁慧1，高文杰2

(1.長春金融高等專科學校，長春 130028;2.吉林大學數(shù)學學院，長春 130012)

考慮一類具變指數(shù)源的p-Laplace方程的Dirichlet邊值問題解的爆破性質(zhì)，通過構(gòu)造恰當?shù)妮o助函數(shù)并利用一階微分不等式，得到了解爆破時間的下界估計.

變指數(shù)源;p-Laplace方程;爆破時間下界

0 引 言

考慮如下具變指數(shù)源的p-Laplace方程:

其中:Ω是?n(n≥3)中具光滑邊界的有界區(qū)域;1＜p＜2;初值u0(x)是Ω上的非負連續(xù)函數(shù).本文總假設(shè)連續(xù)函數(shù)q(x)滿足如下條件:

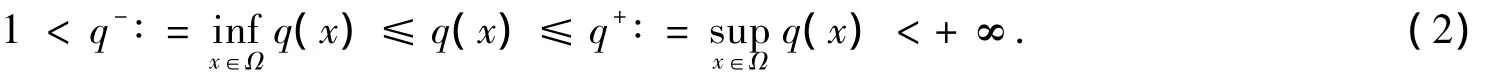
非線性發(fā)展方程(1)可描述物理、化學和生物種群動力學中的很多現(xiàn)象，并可描述牛頓流體的擴散規(guī)律［1-2］.由于非線性擴散或非線性源可能導致方程產(chǎn)生奇性解，因此除了解的適定性外，對形如方程(1)的非線性方程解的奇性研究也是非線性發(fā)展方程的重要內(nèi)容.目前，對發(fā)展方程解的爆破性質(zhì)研究已取得許多結(jié)果［3-7］.

Payne等利用一階微分不等式得到了具齊次Dirichlet邊界條件的半線性熱方程解的爆破時間下界估計［8］，并通過修正該方法，得到了具齊次Neumann邊界條件和Robin邊界條件的半線性熱方程解的爆破時間下界估計［9-10］.文獻［11-13］也利用一階微分不等式研究了不同邊界條件下半線性或擬線性方程爆破時間的下界.

基于此，本文考慮方程(1)解的爆破問題，并給出一定條件下爆破時間的下界估計.方程(1)弱解的局部存在性可以用標準的正則化方法得到［14］.由于q(x)＞1，方程(1)的弱解還是唯一的，且當初值適當大時解在有限時刻爆破［15］.

1 主要結(jié)果

假設(shè)方程(1)的解在有限時刻t*爆破.下面利用一階微分不等式技巧并結(jié)合Sobolev嵌入不等式給出爆破時間t*的下界估計.

定理1 設(shè)q(x)滿足式(2)，u(x，t)是方程(1)的非負解，使得φ(t)在t*時刻爆破，其中

則φ(t)滿足如下一階微分不等式:

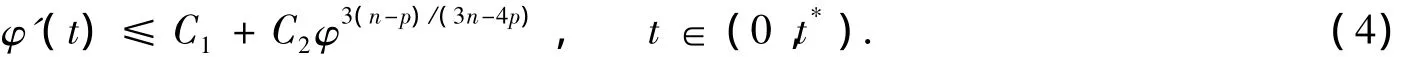
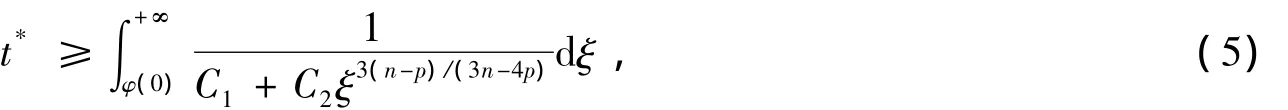
從而可得爆破時間t*的下界估計:其中C1和C2為只依賴于n，p，q(x)，Ω的正常數(shù).

證明:首先對式(3)兩端分別關(guān)于t求導并利用方程(1)和分部積分公式可得

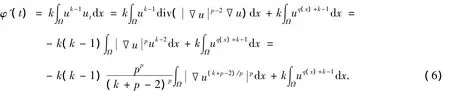
對于任意的時間t＞0，把區(qū)域Ω分成兩部分:

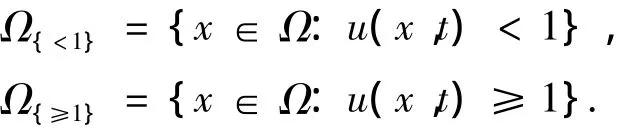
下面估計式(6)的最后一項:

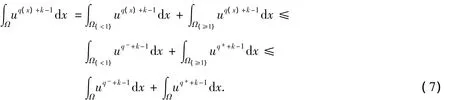
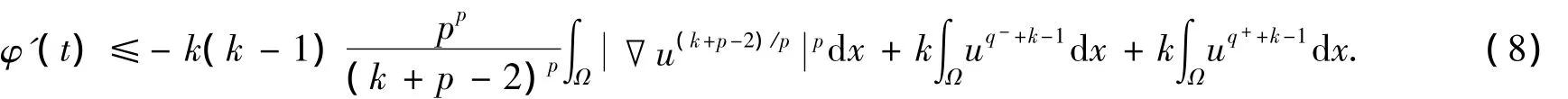
利用H?lder不等式、Young不等式并結(jié)合常數(shù)k的假設(shè)條件，可得

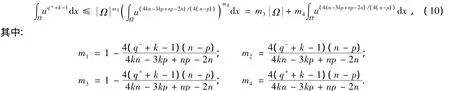
結(jié)合式(8)～(10)可得

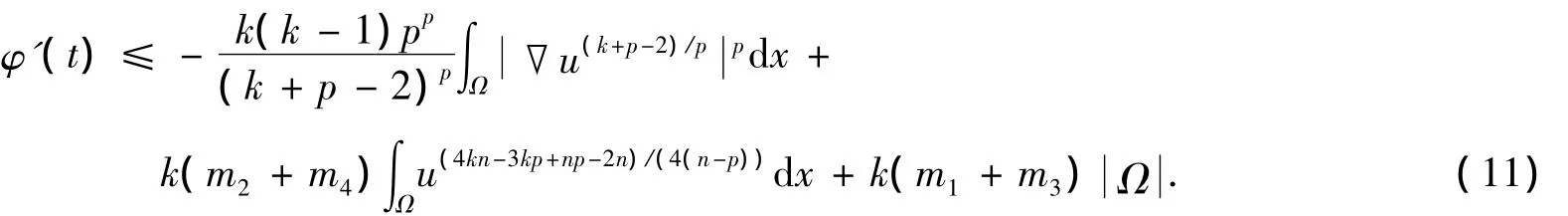
對式(11)右端第二項應(yīng)用Schwarz不等式，有

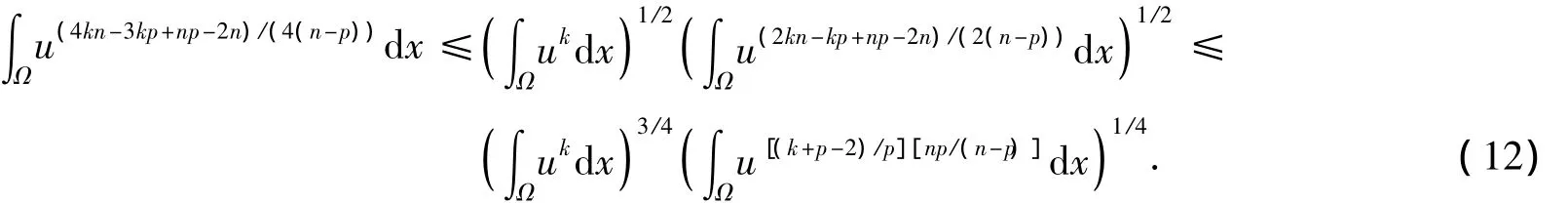
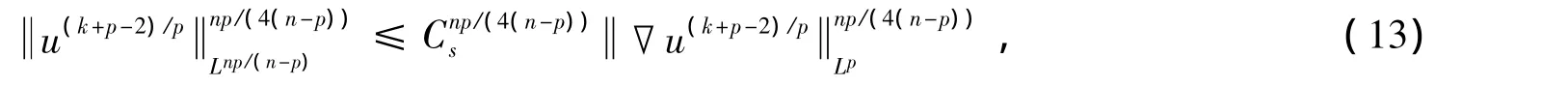
其中Cs是Sobolev嵌入不等式中的最佳常數(shù).

將式(13)代入式(12)，可得

再次利用Young不等式得

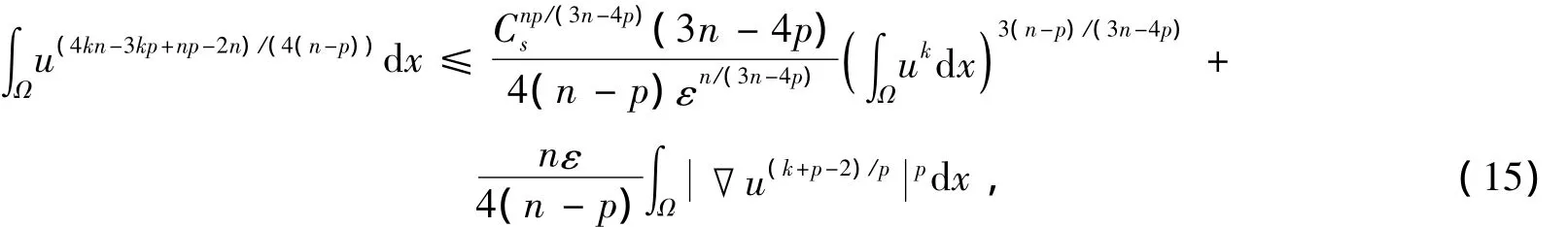
其中ε＞0為待定常數(shù).結(jié)合式(11)和式(15)有

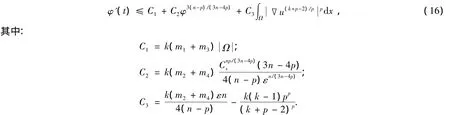
對微分不等式(17)在(0，t)上積分，可得證畢.

注1 定理1可以推廣到具變指數(shù)源的雙重退縮問題:

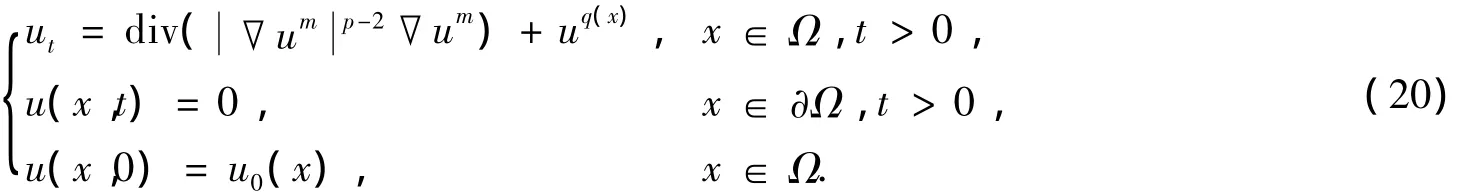
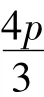
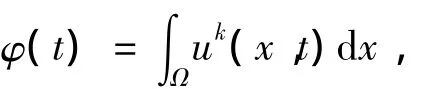
［1］ DiBenedetto E.Degenerate Parabolic Equations［M］.Berlin:Springer，1993.

［2］ WU Zhuoqun，ZHAO Junning，YIN Jingxue，et al.Nonlinear Diffusion Equations［M］.Singapore:World Scientific，2001.

［3］ Kaplan S.On the Growth of Solutions of Quasi-linear Parabolic Equations［J］.Commun Pure Appl Math，1963，16 (3):305-330.

［4］ Fujita H.On the Blowing up of Solutions of the Cauchy Problem for ut=Δ u+u1+α［J］.J Fac Sci Univ Tokyo Sect，1966，13:109-124.

［5］ Kalashnikov A S.Some Problems of the Qualitative Theory of Nonlinear Degenerate Second-Order Parabolic Equations［J］.Russian Math Surveys，1987，42(2):169-222.

［6］ Levine H A.The Role of Critical Exponents in Blow-up Theorems［J］.SIAM Rev，1990，32(2):262-288.

［7］ Lacey A A.Diffusion Models with Blow-up［J］.J Comp Appl Math，1998，97(1/2):39-49.

［8］ Payne L E，Schaefer P W.Lower Bounds for Blow-up Time in Parabolic Problems under Dirichlet Conditions［J］.J Math Anal Appl，2007，328(2):1196-1205.

［9］ Payne L E，Schaefer P W.Lower Bounds for Blow-up Time in Parabolic Problems under Neumann Conditions［J］.Appl Anal，2006，85(10):1301-1311.

［10］ Payne L E，Schaefer P W.Blow-up in Parabolic Problems under Robin Boundary Conditions［J］.Appl Anal，2008，87 (6):699-707.

［11］ Payne L E，Philippin G A，Schaefer P W.Bounds for Blow-up Time in Nonlinear Parabolic Problems［J］.J Math Anal Appl，2008，338(1):438-447.

［12］ Payne L E，Philippin G A，Schaefer P W.Blow-up Phenomena for Some Nonlinear Parabolic Problems［J］.Nonl Anal: Theory，Methods＆Applications，2008，69(10):3495-3502.

［13］ BAO Aiguo，SONG Xianfa.Bounds for the Blowup Time of the Solutions to Quasi-linear Parabolic Problems［J/OL］.Z Angew Math Phys，2013，doi:10.1007/s00033-013-0325-1.

［14］ ZHAO Junning.Existence and Noexistence of Solutions for ut=divp-2▽u)+f(▽u，u，x，t)［J］.J Math Anal Appl，1993，172(1):130-146.

［15］ YIN Jingxue，JIN Chunhua.Critical Extinction and Blow-up Exponents for Fast Diffusive p-Laplacian with Sources［J］. Math Method Appl Sci，2007，30(10):1147-1167.

(責任編輯:趙立芹)

Lower Bounds for the Blow-up Time of Solutions to a Class of p-Laplace Equation with Variable Sources

MENG Fanhui1，GAO Wenjie2
(1.Changchun Finance College，Changchun 130028，China; 2.College of Mathematics，Jilin University，Changchun 130012，China)

This paper deals with the blow-up properties of solutions to a class ofp-Laplace equation with variable sources.Constructing suitable auxiliary functions and making use of the first order differential inequality technique，the authors obtained a lower bound for the blow-up time of solutions to such equations under Dirichlet boundary conditions.

variable source;p-Laplace equation;lower bound for the blow-up time

O175.8

A

1671-5489(2014)03-0435-04

10.13413/j.cnki.jdxblxb.2014.03.06

2013-11-26.

孟繁慧(1965—)，女，漢族，碩士，副教授，從事偏微分方程的研究，E-mail:hui_2182@sina.com.通信作者:高文杰(1956—)，男，漢族，博士，教授，博士生導師，從事偏微分方程的研究，E-mail:wjgao@jlu.edu.cn.

國家自然科學基金(批準號:11271154)和吉林省高教研究重點項目(批準號:吉高教字2012［45］).