一類不定復空間型中Lagrange子流形的Chen型不等式

張 攀，張 量，宋衛(wèi)東

(安徽師范大學數(shù)學計算機科學學院，安徽蕪湖 241000)

一類不定復空間型中Lagrange子流形的Chen型不等式

張 攀，張 量，宋衛(wèi)東

(安徽師范大學數(shù)學計算機科學學院，安徽蕪湖 241000)

利用Riemann不變量和 Riemann流形上的最優(yōu)化方法得到一類不定復空間型中Lagrange子流形的Chen型不等式，并證明了等號成立時子流形一定為全測地的.

不定復空間型;Lagrange子流形;Chen型不等式;全測地

向量，在L中選取局部正交標架場}，使得=X.記RicL(X)義M上的Riemann不變量如下:

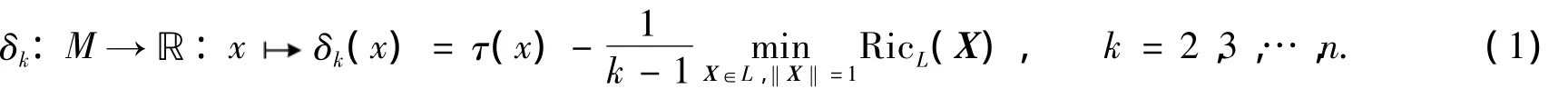
特別地，當k=2時，δk(M)=δM.此外，文獻［11］給出了復空間型中Lagrange子流形的一個Chen型不等式;文獻［12］證明了該Chen型不等式等號成立時當且僅當子流形是全測地的.

定理1 設Mn為(c)中Lagrange類空子流形，n≥4，則Riemann不變量δn(M)滿足

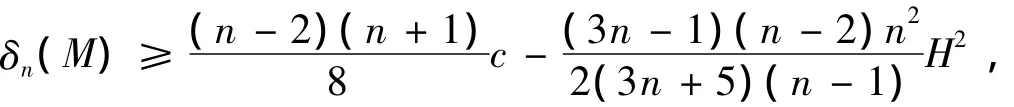
其中H為M的平均曲率.當?shù)忍柍闪r，Mn為全測地子流形.

1 預備知識

設Mn是Nnn/2(c)中實n維Lagrange類空子流形.在(c)上選取局部規(guī)范正交標架場:

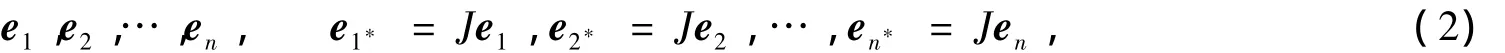
使得其限制于Mn時，{e1，e2，…，en}與Mn相切.本文約定各類指標取值范圍如下:

A，B，C，…=1，2，…，n，1*，2*，…，n*;i，j，k，…=1，2，…，n; α，β，γ，…=1*，2*，…，n*.設ωA為eA的對偶標架場，使得(c)的度量為εi=1;εα=-1.于是，(c)的結(jié)構(gòu)方程為

這里JAB為線性變換J關于{eA}的變換矩陣.

限制在Mn上，有

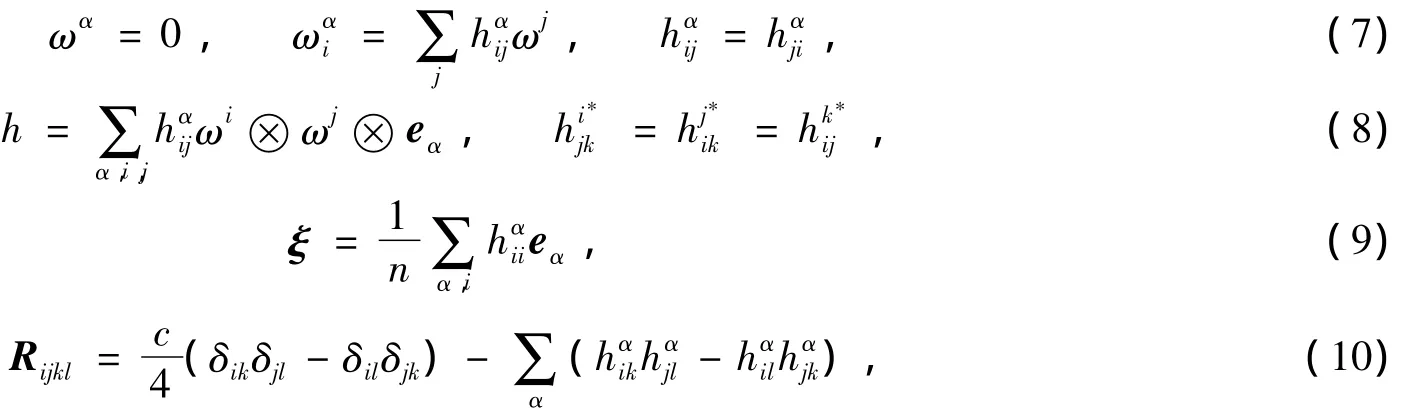
其中h，ξ，Rijkl分別是Mn的第二基本形式、平均曲率向量和曲率張量.定義H=‖ξ‖，Hα=()n×n.

設()為n維Riemann流形，M為N的m維子流形，N上的Riemann度量誘導了M上的Riemann度量g.設f:N→?為可微函數(shù).考慮條件極值問題:

可得:

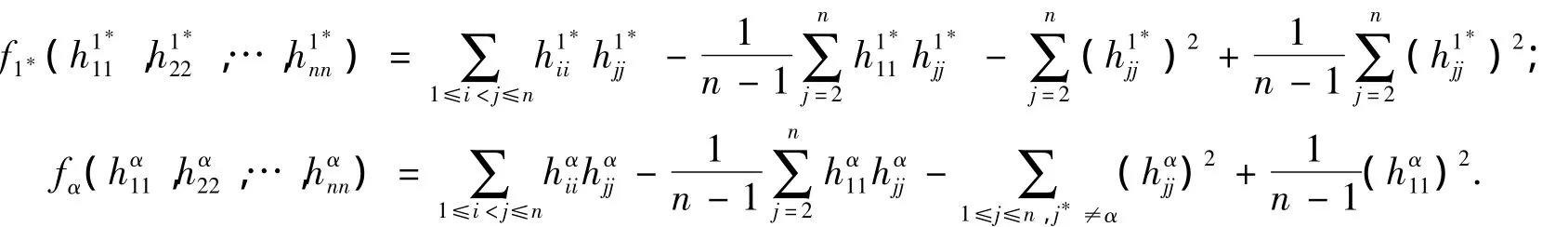
引理1［6］假設x0∈M是問題(11)的解，則:

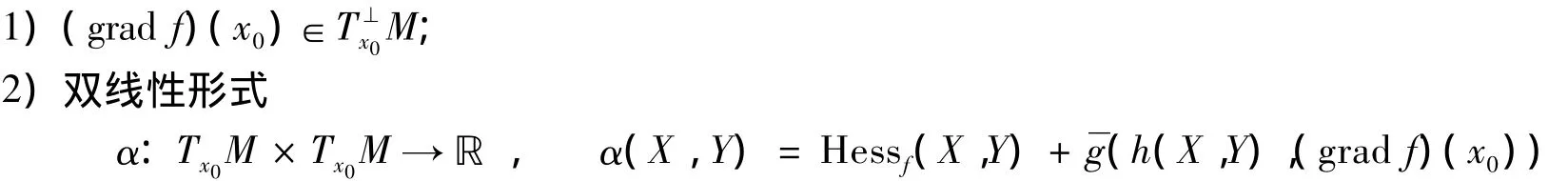
是半負定的，其中:gradf為函數(shù)f的梯度;h為M在N中的第二基本形式.

2 定理1中不等式的證明

對任意的x∈M，設單位切向量X∈TxM，且Mn在x點沿X方向的Ric曲率最小，在TxM和M中分別取標準正交基{e1，e2，…，en}和，…，}，使得e1=X.如果L=TxM，則由式(1)得

又由式(8)可得

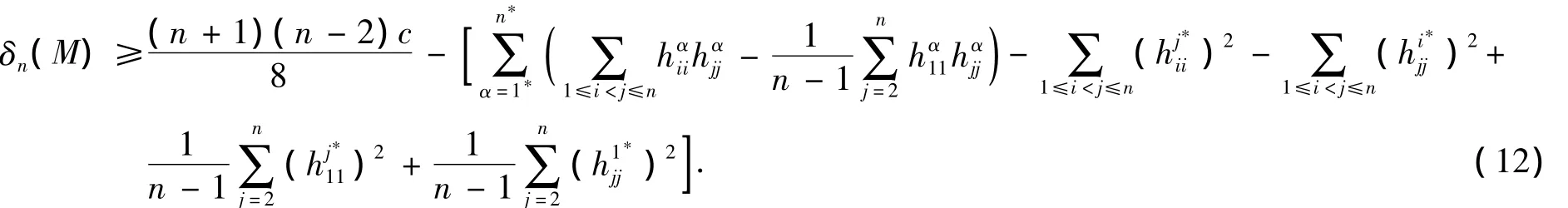
上，其中k1*為常數(shù).對函數(shù)f1*關于每個自變量求偏導，有

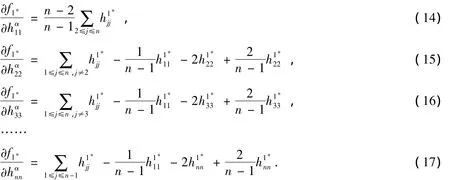
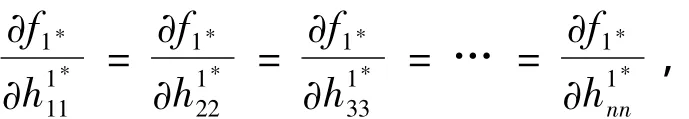
則由式(13)～(17)可得

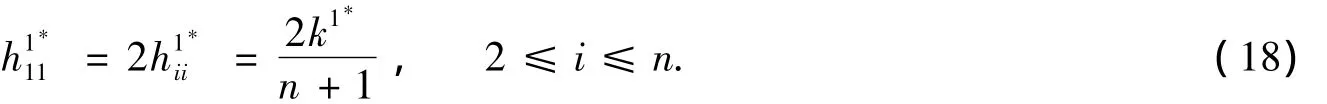
設q為P上的任意一點，則雙線性形式α:TqP×TqP→?為

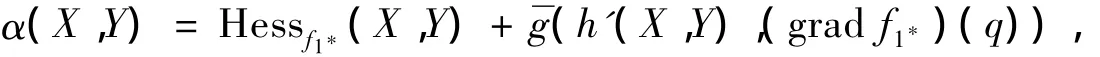
其中:h'為P上的第二基本形式;為?n上的Riemann度量.在?n的自然標架場下，的Hesse矩陣為

因為P為?n中的全測地子流形，考慮X∈TqP，易見

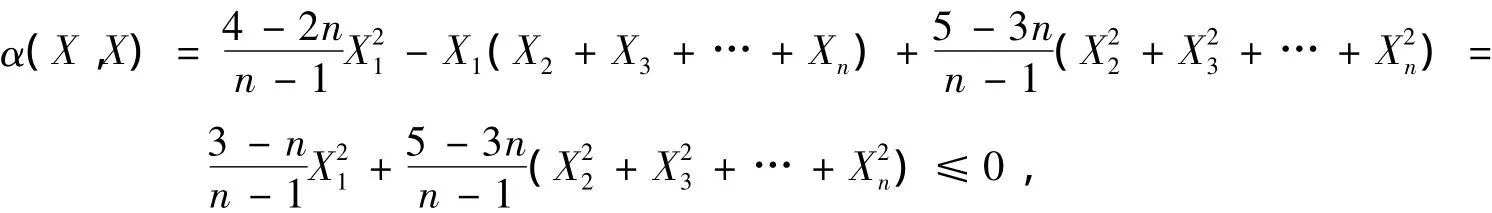
所以為凸函數(shù)，于是由式(18)給出的(，，…，)是最大值點，因此

考慮問題maxfα(α=2*，3*，…，n*)，限制在P:++…+=kα上，其中kα為常數(shù).同理可得fα的(，…，hαnn)最大值點滿足

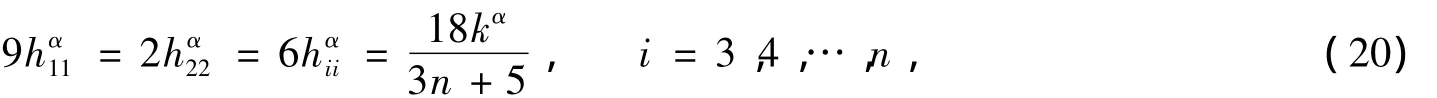
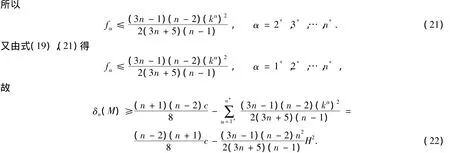
3 定理1中等號成立的證明

命題1 設Mn為(c)中Lagrange類空子流形，n≥3，x∈Mn，則δn(x)滿足

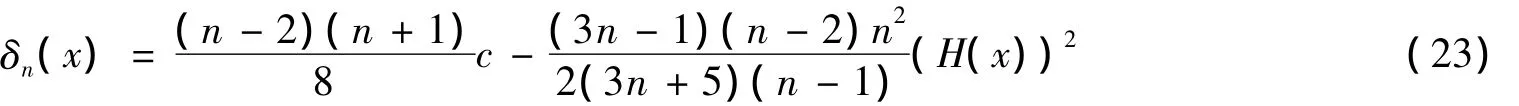
當且僅當TxM中存在標準正交基{e1，e2，…，en}，使得

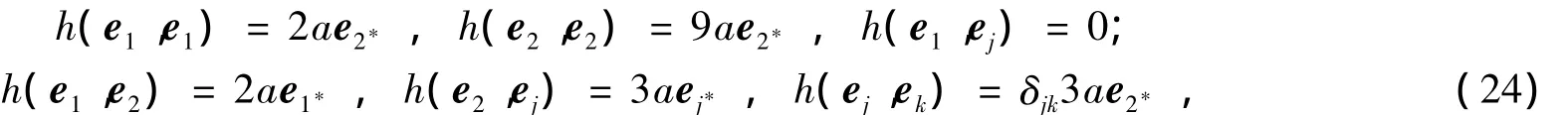
其中a為Mn上的函數(shù)，且j，k=3，4，…，n.

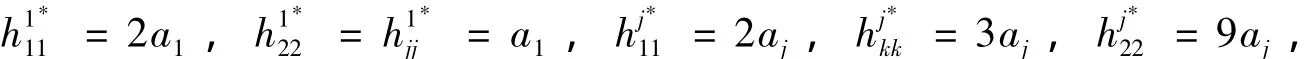
其中j，k=3，4，…，n且j≠k.

當?shù)忍柍闪r，注意到式(19)和式(21)，必有a1=0.在切空間TxM和法空間中分別取標準正交基{e1，e2，…，en}和，…，}，使得ξ=，再由式(8)可得式(24).證畢.

下面證明定理1中等號成立的結(jié)論.假設δn(x)滿足式(23)，Mn不是全測地的，不妨假設在x點h(x)≠0.由命題1知，TxM中存在標準正交基{e1，e2，…，en}，使得式(24)成立.注意到h(x)≠0，則a≠0.因為與平均曲率向量平行，所以可以在x點的一個開鄰域Ox將擴充為一個可微向量場，使得與平均曲率向量場平行.所以在開鄰域Ox內(nèi)任一點，Weingarten變換有3個特征值:2a，9a和3a，且重數(shù)分別為1，1，n-2.于是可將TxM的正交基{e1，e2，…，en}擴充為開鄰域Ox的局部標準正交基，使得對Ox內(nèi)任一點都有式(24)成立.

因為Mn為(c)的不變子流形［14］，所以對Mn上任意切向量場X，Y，Z，有

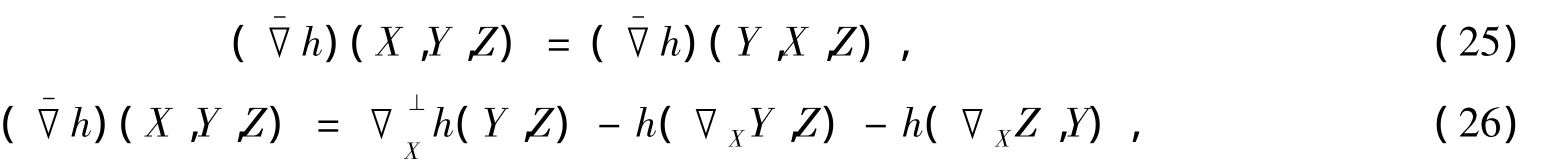
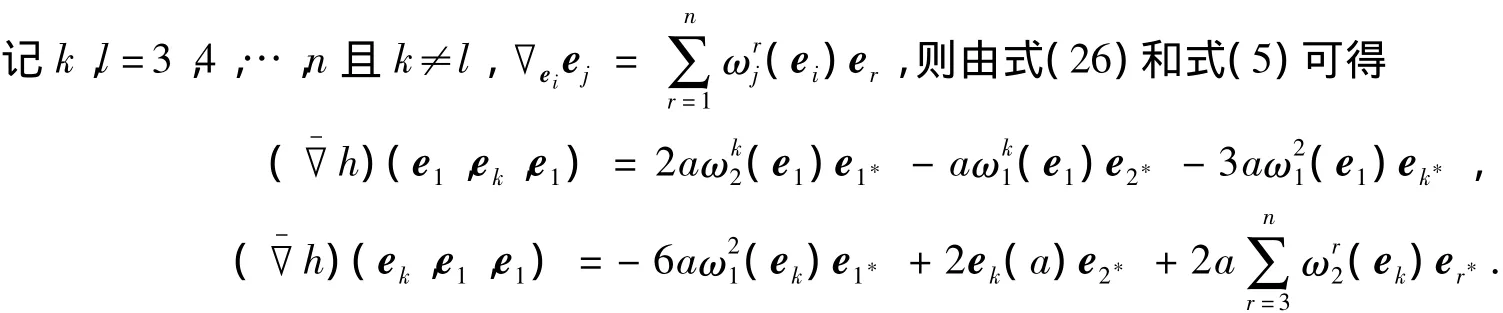
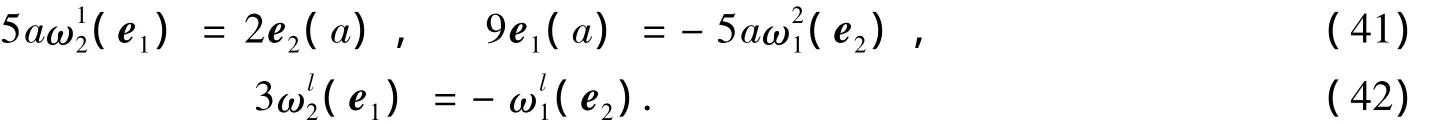
由式(29)，(33)可得ek(a)=0，再結(jié)合式(27)可得=0.由式(27)，(31)可得=0，再結(jié)合式(29)有=0.由式(40)，(41)有e1(a)=0，再結(jié)合式(32)有)=0.注意到式(34)，故有=0.由式(28)，(37)，(41)有)=0，再結(jié)合式(30)，(36)，(38)有=0.又由式(37)有

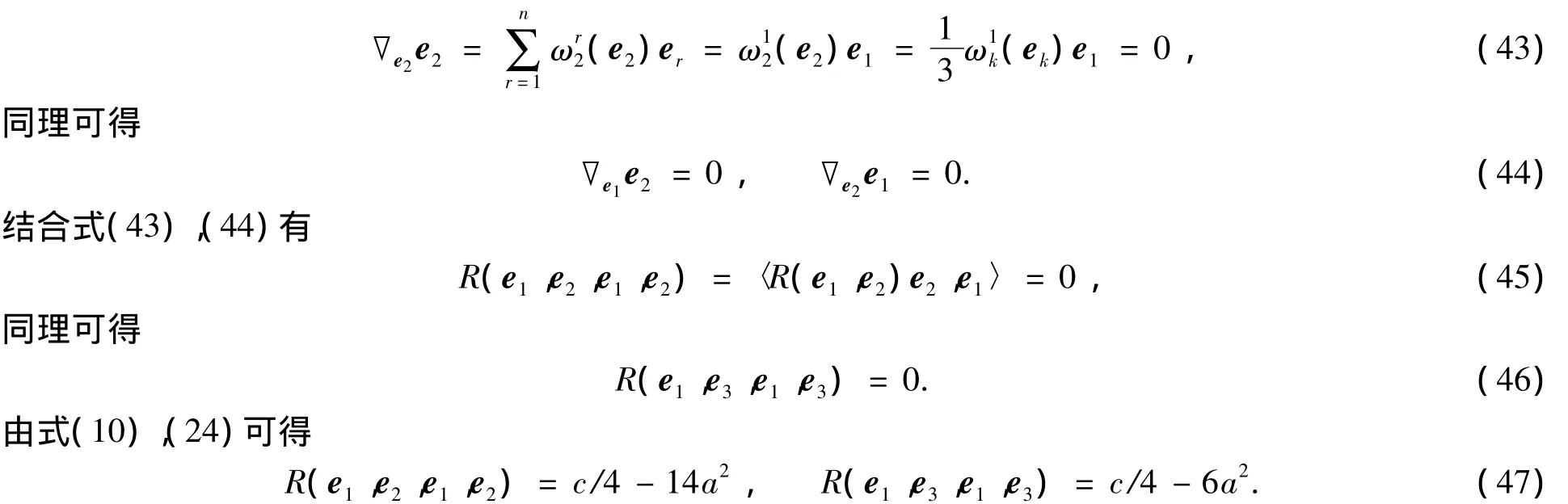
結(jié)合式(45)～(47)有a=0，這與a≠0的假設矛盾.故必有a=0，則Mn為全測地子流形.

［1］ CHEN Bangyen.Some Pinching and Classification Theorems for Minimal Submanifolds［J］.Arch Math，1993，60:568-578.

［2］ Chern S S.Minimal Submanifolds in a Riemannian Manifold［M］.Lawrence:University of Kansas Press，1968.

［3］ Chen B Y，Dillen F，Verstraelen L，et al.Totally Real Submanifolds of CPnSatisfying a Basic Equality［J］.Arch Math，1994，63(6):553-564.

［4］ Defever F，Mihai I，Verstraelen L.B.-Y.Chen’s Inequality for Submanifolds of Sasakian Space Forms［J］.Boll Unione Mat Ital，2001，4B(2):521-529.

［5］ Gülbahar M，Kilic E，Keles S.Chen-Like Inequalities on Lightlike Hypersurfaces of a Lorentzian Manifold［J］.Journal of Inequalities and Applications，2013，2013(1):266.

［6］ Oprea T.Optimizations Methods on Riemannian Submanifolds［J］.An Univ Buc，2005，1:127-136.

［7］ Oprea T.Chen’s Inequality in Lagrangian Case［J］.Colloq Math，2007，108:163-169.

［8］ Bolton J，Montealegre C R，Vrancken L.Characterizing Warped Product Lagrangian Immersions in Complex Projective Space［J］.Proc Edinb Math Soc，2009，52(2):273-286.

［9］ Tripathi M M.Improved Chen-Ricci Inequality for Curvature-Like Tensors and Its Applications［J］.Differential Geometry and Its Applications，2011，29(5):685-698.

［10］ CHEN Bangyen.Relations between Ricci Curvature and Shape Operator for Submanifolds with Arbitrary Codimensions［J］.Glasg Math J，1999，41(1):33-41.

［11］ Oprea T.On a Riemannian Invariant of Chen Type［J］.Rocky Mountain J Math，2008，38(2):567-581.

［12］ Dillen F，F(xiàn)astenakel J.On an Inequality of Oprea for Lagrangian Submanifolds［J］.Cent Eur J Math，2009，7(1): 140-144.

［13］ CHEN Bangyen，Dillen F.Classification of Marginally Trapped Lagrangian Surfaces in Lorentzian Complex Space Forms［J］.Journal of Mathematical Physics，2007，48(1):013509.

［14］ CHEN Bangyen，Ogiue K.On Totally Real Submanifolds［J］.Trans AMS，1974，193:257-266.

(責任編輯:趙立芹)

Inequalities of Chen Type for Lagrangian Submanifolds of a Class of Indefinite Complex Space Form

ZHANG Pan，ZHANG Liang，SONG Weidong
(College of Mathematics and Computer Science，Anhui Normal University，Wuhu 241000，Anhui Province，China)

We obtained an inequality of Chen type for Lagrangian submanifolds of a class of indefinite complex space form using the Riemannian invariant and the optimization method on the Riemannian manifolds.In particular，we also showed that a Lagrangian submanifold of the indefinite complex space form attaining equality in the inequality must be totally geodesic.

indefinite complex space form;Lagrangian submanifolds;inequality of Chen type;totally geodesic

O186.12

A

1671-5489(2014)03-0439-06

10.13413/j.cnki.jdxblxb.2014.03.07

0 引言及主要結(jié)果

2013-07-15.

張 攀(1991—)，男，漢族，碩士研究生，從事微分幾何的研究，E-mail:zhangpan1991622@sina.com.通信作者:張 量(1979—)，男，漢族，碩士，副教授，從事微分幾何的研究，E-mail:zhliang43@sohu.com;宋衛(wèi)東(1958—)，男，漢族，教授，從事微分幾何的研究，E-mail:swd@sina.com.

安徽省高校優(yōu)秀青年人才基金(批準號:2011SQRL021ZD).