橋式起重機吊重偏擺系統的動力學仿真

薛 偉，萬 雷

(東北林業大學 工程技術學院，哈爾濱 150040)

橋式起重機采用鋼絲繩連接起重小車和吊裝的重物，這種柔性連接方式一方面減少了起升時的沖擊載荷，另一方面，由于慣性的影響，吊重在橫向搬運時的速度與起重小車的速度不同步，使得吊重在鋼絲繩末端做小幅度球面擺動，擺動過程從大、小車的加速起動階段到穩定運行階段再到減速制動階段持續進行，吊重的擺動進而影響了大、小車運行的速度特性。吊重擺動角度的控制和起重小車的準確定位是一個關乎生產安全和生產效率的問題，而對吊擺系統振動特性的研究是對其控制方案設計的基礎和參照。

針對吊擺系統的代表性研究中，鐘斌將吊擺系統簡化為二維質點系運動，采用矢量力學建立了系統的數學模型[1]；薛偉應用拉格朗日方程建立了吊擺系統的4自由度動力學分析模型[2]，首次考慮了吊重的長度對擺動的影響并引入“質桿”作為其中一個研究對象；Lee在建模基礎上，分別采用模糊控制和神經網絡控制兩種方法進行防擺控制[3]；杜文正針對小車位移特性和吊重擺角特性分別設計了兩個PID控制器[4]。

1 吊擺系統的動力學模型

1.1 模型建立的基本假設

對吊擺系統做以下3個基本假設作為建模的必要條件：

(1)小車和吊重分別簡化為質點O和A，質量分別為M和m，不計吊重的水平扭轉。

(2)鋼絲繩有足夠的強度和剛度，忽略鋼絲繩因受力而引起的微小形變。

(3)忽略鋼絲繩的質量以及鋼絲繩和滑輪組之間的摩擦。

1.2 吊擺系統動力學模型的建立

文獻[5]研究表明，吊重在鋼絲繩末端做的小幅度球面擺動可以看作分別在大車和小車運行方向上做類似單擺運動的合成。在微擺條件下，某一方向上的擺角只與該方向上的速度特性和該平面內擺動阻尼有關而與其他方向上的因素無關。由于大、小車對各自運動平面內擺角的影響規律相同，且復合運動的研究較復雜，這里假設大車停止，只選擇吊擺系統在平面XOZ內的運動作為研究對象，研究轉化為3自由度平面運動問題。

起重機工作時，水平搬運和豎直起吊兩過程不同時進行，豎直起吊時小車制動，擺角近似為0[6]，故本文只研究水平搬運過程。吊擺系統模型如圖1所示。

圖1 吊擺系統模型示意圖

建立坐標系XOZ，其中：小車起始位置為坐標原點O，X和Z兩個軸向分別代表小車運行和吊重升降的方向，OB為鉛垂線，OA為繩長(擺線長度)，∠AOB為擺線與鉛垂線二維夾角。記∠AOB=θ，OA=l，吊擺系統的模型如圖1所示。

設小車質心坐標(XM，ZM)=(x，0)，則吊重質心坐標(Xm，Zm)=(x+lsinθ,-lcosθ)。

小車和吊重的速度分量分別是它們位置坐標的一階導數：

在忽略掉一些次要因素并做出必要的假設后，起重機吊擺系統就是一個典型的動力學系統。在分析這類小幅度振動問題時，可以用質點系的動能、勢能和廣義力之類的純量來描述總體系，本論文采用拉格朗日方程來建立起重機吊擺系統的數學模型。

拉格朗日方程的一般形式如下：

(1)

式中：L為拉格朗日函數，L=T-V，T為系統的動能；V為系統的勢能；qj為廣義坐標；Qj為廣義力。

吊擺系統的動能：

(2)

吊擺系統的重力勢能：

V=-mglcosθ。

(3)

拉格朗日函數：

(4)

將(4)式帶入(1)式的拉格朗日方程：

(5)

1.3 模型的線性化處理

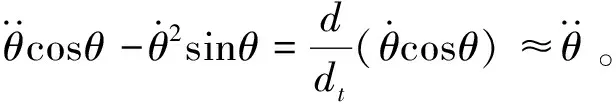
(6)

2 吊擺系統動力學仿真

2.1 仿真的數學模型

(1)小車起停階段。小車由靜止經電動機驅動加速運行到電動機停止驅動后小車被制動最終停止，研究吊擺系統在時域內的變化。由于鋼絲繩的擺動阻尼對偏擺運動起抑制作用，故起停階段忽略鋼絲繩阻尼，(6)改寫為左端只保留二階導數的形式(7)：

(7)

(8)

2.2 實例仿真

選擇QD32/5型號起重機作為實例仿真對象，額定起重量32 t，跨度22 m，最大起升高度13 m，小車質量11.5 t，小車運行電動機YZR160M-1(功率6.3 kW，轉速921 r/min)，制動器JWZ9-200/E23(制動力矩200 N·m)。應用Matlab/Simulink軟件分別對2.1中的公式(1)和公式(2)兩階段的三種工況：①m=25 t，l=10 m；②m=25 t，l=5 m；③m=12.5 t，l=10 m進行仿真。

(1)起停階段仿真時間12 s，其中電動機驅動8s，制動作用4 s。小車的運動曲線如圖2和圖3所示，吊重的擺動曲線如圖4和圖5所示。

(2)制動后吊重的擺動，鋼絲繩擺動阻尼600 N·s/m，仿真時間120 s，吊重在不同工況下的擺動角速度如圖6和圖7所示。

圖2 速度—時間曲線圖

圖3 位移—時間曲線

圖4 角速度—時間曲線

圖5 擺角—時間曲線

圖6 不同繩長的角速度—時間曲線

圖7 不同吊重質量的角速度—時間曲線

3 結 論

結合橋式起重機工作特點，應用分析力學建立了吊重偏擺系統的動力學模型，選取QD32/5型號起重機作為研究對象，采用Matlab/Simulink軟件對小車起停階段和制動后吊重的擺動情況進行仿真，得到了小車的運動特性和吊重的擺動特性。

(1)電動機驅動下，吊重后擺使小車速度呈現加速和勻速的周期性交替變化，3種工況下的周期分別約為1、1和2 s；制動時吊重的前擺程度較大，小車速度整體呈下降趨勢的過程中有周期性短暫加速，小車的速度不能穩定。工況①和②的位移曲線基本重合，說明影響小車定位的主要因素是吊重質量，而鋼絲繩長度的影響較小。

(2)吊重在電機驅動和制動器制動作用下做受迫擺動，兩階段周期基本相同；3種工況下，起動階段最大擺角分別為0.03、0.03和0.05 rad；制動階段最大擺角分別為0.12、0.12和0.18 rad。可見，對吊重系統擺角的控制主要是針對制動階段。

(3)小車制動停止后，吊重做有阻尼擺動，擺動周期分別為6.8、4.2和4.2 s，擺動完全消除需要的時間較長，都超過120 s。工況①和②的對比說明繩長主要影響擺動周期，縮短繩長可以使擺動周期減小，但增大了約0.2 rad/s的擺動角速度；工況①和③的對比說明吊重質量越小，擺動減弱的越快。

該分析模型和仿真結果接近實際情況，描述的吊運貨物時吊擺系統的運動情況，為小車定位控制和吊重的擺動控制提供了基礎，具有一定的實際意義。

【參 考 文 獻】

[1]鐘 斌，程文明，馬莉麗，等.起重機小車吊重動力學系統狀態空間重構[J].西南交通大學學報，2007，42(4)：436-441.

[2]薛 偉，郭永娟.林用起重機起吊木捆偏擺系統的動力學模型與仿真[J].東北林業大學學報，2011，39(6)：87-89.

[3]Lee H，Kun C S.A new fuzzy-logic anti-sway control for industrial three-dimensional overhead cranes [A].Proceeding of the 2001 IEEE International Conference on Robotic&Automation [C]，2001(5)：2956-2961.

[4]杜文正，童國林，強寶民，等.基于模糊自適應PID控制器的橋式起重機定位與防擺控制研究[J].制造業自動化，2012，34(11)：8-11.

[5]張則強.橋式起重機吊重二自由度擺角模型與仿真[J].西南交通大學學報，2006，41(6)：696-699.

[6]楊會珍，李 虹，趙 勇.門式起重機的減擺PID控制系統[J].起重運輸機械，2012(11)：16-20.

[7]王玥媛.基于模糊控制的橋式起重機防擺研究[D].大連：大連理工大學，2008.