帶形狀參數的Bernstein-Bézier曲面*
嚴蘭蘭
(東華理工大學理學院,江西 撫州 344000)
帶形狀參數的Bernstein-Bézier曲面*
嚴蘭蘭
(東華理工大學理學院,江西 撫州 344000)
雖然三角域上的曲面造型方法能有效解決不規則產品的幾何造型問題, 在實際工程中有著廣泛的應用, 但由于其結構的特殊性和復雜性, 目前對三角域曲面的擴展研究并不多。為了豐富三角域曲面的理論, 針對如何增強三角域曲面形狀表示的靈活性進行了專門的研究。首先構造了一組三角域上含一個參數的四次多項式基函數, 它是三角域上二次Bernstein基函數的擴展。然后用遞推的方式定義了三角域上含一個參數的n+2次多項式基函數, 它是三角域上n次Bernstein基函數的擴展。基于新的n+2次多項式基函數, 定義了相應的n階三角域曲面。分析了基函數和曲面的性質, 新曲面不僅具備三角域上Bernstein-Bézier曲面的基本性質, 而且還可以在不改變控制頂點的情況下, 通過改變參數的值來自由調整曲面的形狀。
曲面設計;形狀參數;三角域;Bernstein-Bézier曲面
1 引言
Bézier方法因為簡單、直觀而成為計算機輔助幾何設計中最常用的造型方法之一。傳統的Bézier方法既包括Bézier曲線、四邊域上的張量積Bézier曲面, 還包括三角域上的Bernstein-Bézier曲面。這三者在形狀表示方面各有各的優點, 但它們有一個共同的缺點, 就是不具備形狀可調性, 即在控制頂點固定的情況下, 它們的形狀是無法改變的。針對Bézier曲線的這一缺點, 目前已經有很多文獻提出了改進方法[1~4]。這些文獻中的方法可以歸納為, 通過構造含參數的、性質類似于Bernstein基函數的新的基函數, 使得由之定義的曲線在具備Bézier曲線基本性質的同時, 又具備形狀可調性。由于四邊域上的張量積Bézier曲面是Bézier曲線向曲面的直接推廣, 所以這些文獻中的方法在克服Bézier曲線的缺點的同時, 也克服了張量積Bézier曲面的缺點。但是,由于定義在三角域上的Bernstein-Bézier曲面結構的特殊性, 這些文獻中的方法不能直接推廣至三角域曲面, 因此, 必須單獨為三角域曲面構造含參數的基函數, 使得由之定義的曲面具備形狀可調性。
但是,目前關于這方面的研究成果很少, 迄今為止, 僅見到以下成果:鄔弘毅等[5]給出的三角域上帶多個形狀參數的Bézier曲面, 由于該方法中的參數較多, 無疑增加了構造曲面的復雜性。曹娟等[6]給出的三角域上帶一個形狀參數的三次Bernstein-Bézier曲面的擴展曲面, 于立萍[7]給出的三角域上帶兩個形狀參數的三次Bernstein-Bézier曲面的擴展曲面, 都具有靈活的形狀, 但這兩種方法都僅僅只解決了三次Bernstein-Bézier曲面的形狀調整問題, 不具備一般性。吳曉勤等[8]、CAO Juan等[9]、Yan Lan-lan等[4]給出的三角域上帶一個形狀參數的任意n次Bernstein-Bézier曲面的擴展曲面, 都較好地解決了三角域曲面的形狀調整問題, 并且都具有一般性。
為了提供更多的含參數的三角域曲面造型方法, 進一步充實現有的CAD系統, 本文在文獻[4,8,9]的基礎上構造了一種新的結構和性質類似于Bernstein-Bézier曲面的三角域曲面, 并通過實例表明該方法是正確有效的。
2 基函數的構造與性質
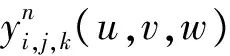
(1)
(2)
類Bernstein-Bézier基函數具有下列性質:
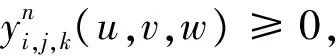
證明用數學歸納法。當n=2時, 類Bernstein-Bézier基函數可以表示成四次Bernstein-Bézier基函數的線性組合, 即:
(3)
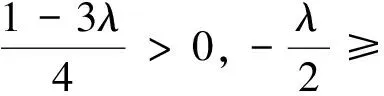
假設r階類Bernstein-Bézier基函數非負, 當n=r+1時, 由式(2)有:
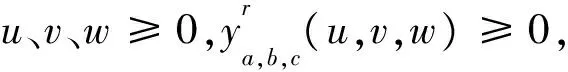
□
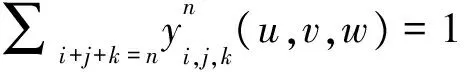
證明用數學歸納法。當n=2時, 由式(3)有:
假設當n=r時規范性成立, 當n=r+1時, 由式(2)有:
證畢。
□
(3) 輪換對稱性。對u、v、w≥0,u+v+w=1,有:
(4)
其中,i、j、k∈N,i+j+k=n,n≥2。
證明用數學歸納法。當n=2時, 由式(3)以及四次Bernstein-Bézier基函數的對稱性, 可知式(4)對n=2成立。假設式(4)對n=r成立, 由這一假設以及式(2), 可知當n=r+1時, 有:
其它幾種關系類似可證。
□
(4) 角點性質。當n≥2時, 對于i、j、k∈N,i+j+k=n, 有:
(5)
證明用數學歸納法。當n=2時, 對式(1)直接計算可知式(5)的正確性。假設式(5)對n=r成立, 當n=r+1時,
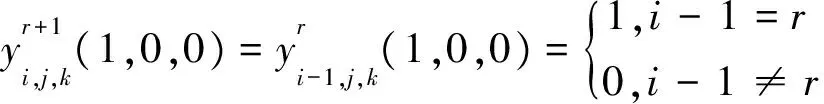

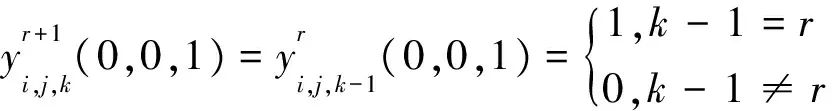
這些表明式(5)對n=r+1成立。證畢。
□
(5)角點導數。對u、v、1-u-v≥0,i、j、k∈N,i+j+k=n,n≥2, 有:
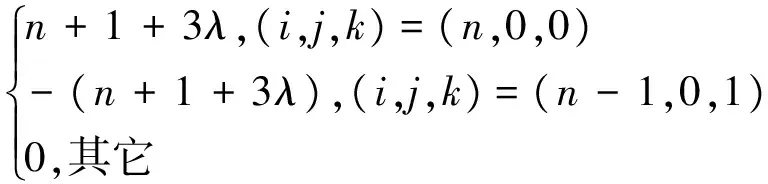
(6)

(7)
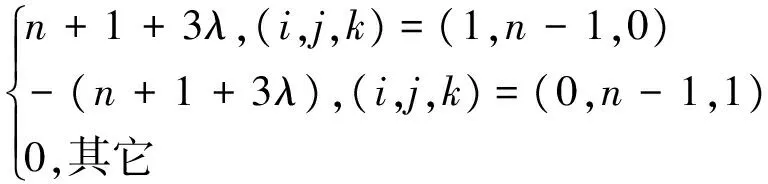
(8)
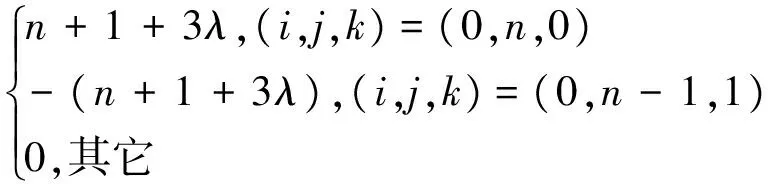
(9)
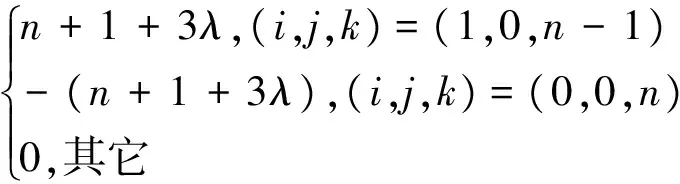
(10)
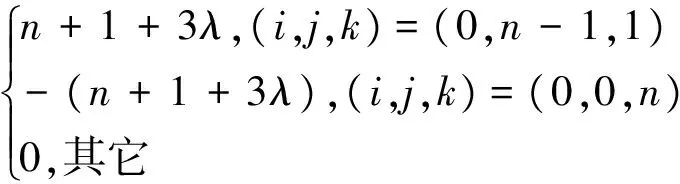
(11)
證明用數學歸納法。當n=2時, 直接計算易知式(6)~式(11)對n=2成立。假設式(6)對n=r成立, 當n=r+1時, 由式(2)有:
(12)
在式(12)兩端對u求導, 得到:
取點(u,v,1-u-v)=(1,0,0), 得到:
由式(5)中所列的在角點(1,0,0)處的性質, 以及歸納假設, 可得:
① 若(i-1,j,k)=(r,0,0), 即(i,j,k)=(r+1,0,0), 則:
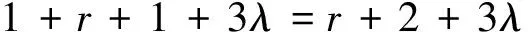
② 若(i,j,k-1)=(r,0,0), 即(i,j,k)=(r,0,1), 則:
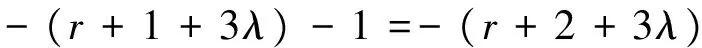
③ 若(i-1,j,k)≠(r,0,0)且(i,j,k-1)≠(r,0,0), 即(i,j,k)≠(r+1,0,0)且(i,j,k)=(r,0,1), 則:
這些結論表明式(6)對n=r+1成立。類似可證式(7)~式(11)也對n=r+1成立。
□
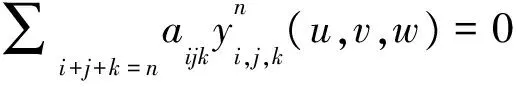
證明充分性是顯然的。下面用歸納法證明必要性。假設對所有的u、v、w≥0,u+v+w=1,有:
(13)
其中aijk∈R,i、j、k∈N,i+j+k=2。將式(3)代入式(13)并整理, 得到:
由四次Bernstein-Bézier基函數的獨立性, 可得式(14)。
將式(14)中的式(14-a)代入式(14-b)中, 可得式(15)。
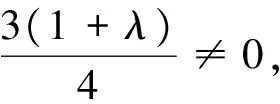
假設r階類Bernstein-Bézier基函數線性無關, 下面證明r+1階類Bernstein-Bézier基函數也線性無關。
(14)
(15)
假設對所有的u、v、w≥0,u+v+w=1, 有:
(16)
其中aijk∈R,i、j、k∈N,i+j+k=r+1。將式(2)代入式(16)并整理, 得到:
由u、v、w的任意性可得:
(17)
由歸納假設及式(17)中的式(17-a)可知, 對所有i、j、k∈N,i+j+k=r+1, 當i≥1時,aijk= 0;由式(17)中的式(17-b)可知, 對所有i、j、k∈N,i+j+k=r+1, 當j≥1時,aijk=0; 由式(17)中的式(17-c)可知, 對所有i、j、k∈N,i+j+k=r+1, 當k≥1時,aijk=0。故對所有的i、j、k∈N,i+j+k=r+1, 有aijk=0。這表明r+1階類Bernstein-Bézier基函數線性無關。
□
3 曲面的構造與性質
定義2給定(n+1)(n+2)/2個控制頂點Vi,j,k∈R3(i、j、k∈N,i+j+k=n), 三角域D= {(u,v,w)|u、v、w≥0,u+v+w=1},其中(u,v,w)為D中點的重心坐標, 稱:
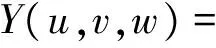
(18)
為定義在三角域D上的帶參數的n階類Bernstein-Bézier曲面。
由類Bernstein-Bézier基函數的性質, 容易推出類Bernstein-Bézier曲面具有下列性質:
(1) 凸包性。類Bernstein-Bézier曲面位于控制網格所在的凸包內。
(2) 仿射不變性。類Bernstein-Bézier曲面的形狀和位置與坐標系的選擇無關, 對曲面作仿射變換, 只需對其網格作此仿射變換。
(3) 角點插值性。曲面的3個角點分別插值于控制網格的3個角點, 即:
(4) 角點切平面。曲面在角點(1,0,0)、(0,1,0)、(0,0,1)處的切平面分別為由控制頂點Vn,0,0、Vn-1,1,0、Vn-1,0,1;V0,n,0、V1,n-1,0、V0,n-1,1;V0,0,n、V1,0,n-1、V0,1,n-1張成的平面。
(5) 形狀可調性。給定控制頂點, 普通Bernstein-Bézier曲面的形狀就唯一確定了, 而對于類Bernstein-Bézier曲面而言, 即使不改變控制頂點, 其形狀依然可以通過改變λ的值進行調整。
圖1和圖2給出了在相同的控制網格下, Bernstein-Bézier曲面與類Bernstein-Bézier曲面的對照圖。其中圖1a、圖2a分別為二次、三次Bernstein-Bézier曲面, 圖1b~圖1f、圖2b~圖2f分別為帶參數λ=-1、-3/4、-1/2、-1/4、0的二階、三階類Bernstein-Bézier曲面。從圖中可以看出,λ越大, 類Bernstein-Bézier曲面越接近其控制網格。
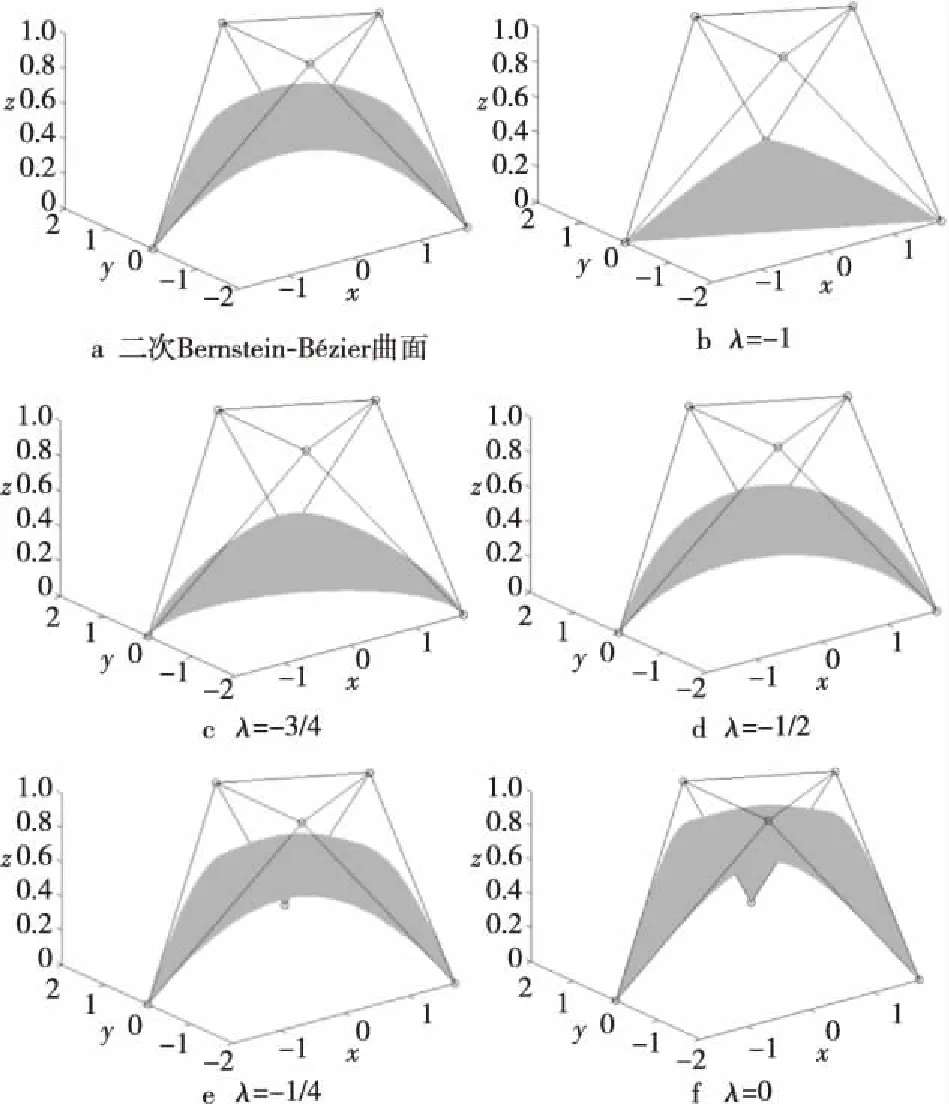
Figure 1 Contrast of the quadratic Bernstein-Bézier surface and the Bernstein-Bézier surface of order two圖1 二次Bernstein-Bézier曲面與 二階類Bernstein-Bézier曲面的對照圖

Figure 2 The contrast of cubic Bernstein-Bézier surface and the Bernstein-Bézier surface of order three圖2 三次Bernstein-Bézier曲面與 三階類Bernstein-Bézier曲面的對照圖
(6)遞推求值算法。給定參數u、v、w(u、v、w≥ 0,u+v+w=1), 可以用下面的算法來計算n階類Bernstein-Bézier曲面上相應的點Y(u,v,w)。
為了簡潔, 用τ表示u,v,w, 則:
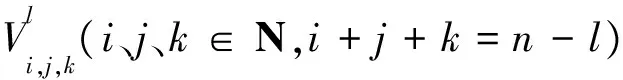
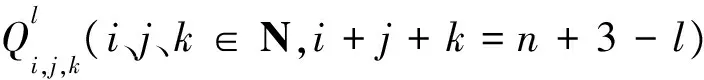
當l=n-1時,
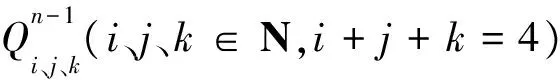
4 參數λ對曲面形狀的影響
在工程實際中主要應用的是低階的曲面, 為了方便應用, 下面分析參數λ的取值對二階、三階類Bernstein-Bézier曲面形狀的影響。
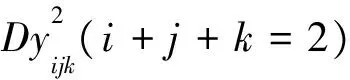
上面的結果表明,y200、y020、y002是關于λ的遞減函數, 而y110、y011、y101是關于λ的遞增函數。基函數的這種性質反映在二階類Bernstein-Bézier曲面的圖形上的特點是:在參數λ允許的范圍內,λ的值越大, 曲面越遠離由三個角點V200、V020、V002確定的平面, 同時越接近由三個中間點V110、V011、V101確定的平面, 見圖1b~圖1f。
由式(1)和式(2)可知,當n=3時,

(19)
式(19)表明y300、y030、y003是λ的遞減函數。y111是λ的遞增函數。當w=0時,y210、y120是λ的遞增函數; 當u=0時,y021、y012是λ的遞增函數; 當v=0時,y102、y201是λ的遞增函數。基函數的這種性質反映在三階類Bernstein-Bézier曲面的圖形上的特點是:在參數λ允許的范圍內,λ的值越大, 曲面越遠離由三個角點V300、V030、V003確定的平面, 越接近中心點V111, 同時三條邊界曲線分別越接近相應的控制邊V210V120、V021V012、V102V201,見圖2b~圖2f。
5 曲面的造型實例
本文提出的三角域曲面造型方法具有一般性, 任給(n+1)(n+2)/2個控制頂點(n≥2), 選擇恰當的參數λ, 便可以構造出想要的曲面。圖3~圖5給出了類Bernstein-Bézier曲面的造型實例。圖3中的兩張曲面均取參數λ=-1/2;圖4、圖5中的曲面均取參數λ=0。
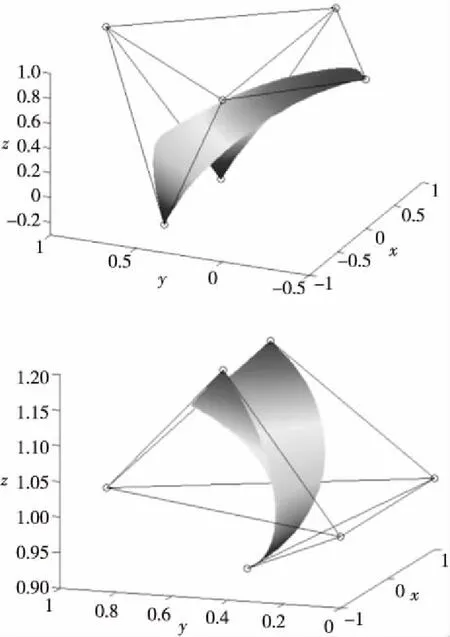
Figure 3 Bernstein-Bézier-like surfaces of order two圖3 二階類Bernstein-Bézier曲面
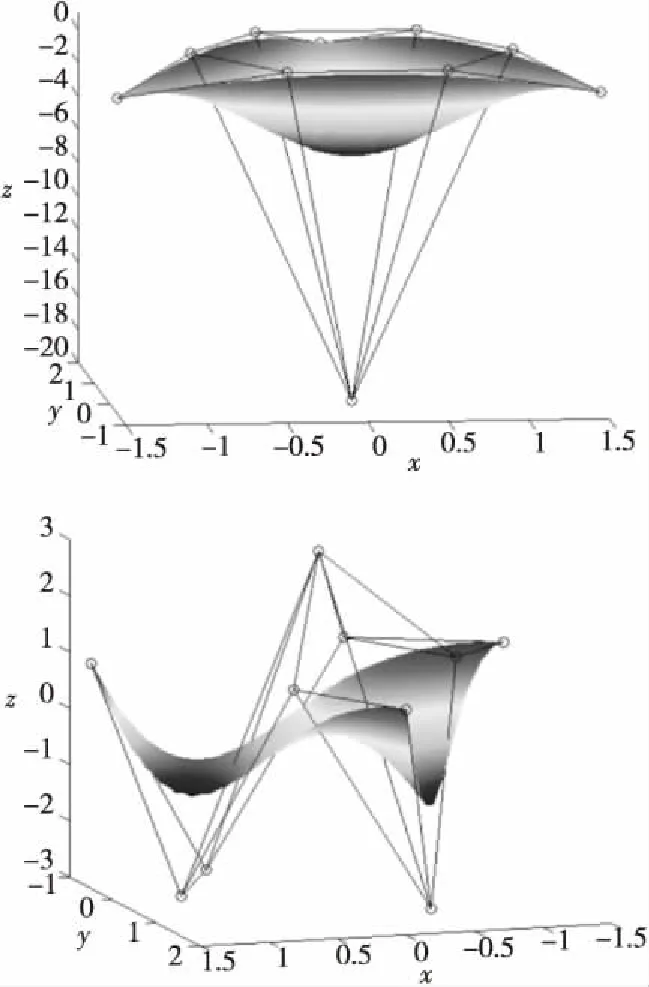
Figure 4 Bernstein-Bézier-like surfaces of order three圖4 三階類Bernstein-Bézier曲面
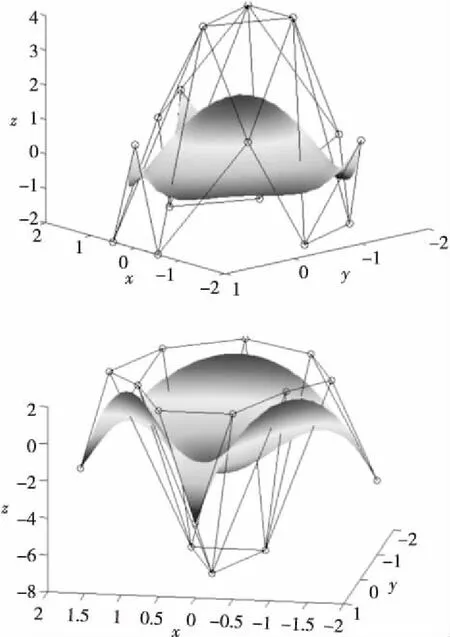
Figure 5 Bernstein-Bézier-like surfaces of order four圖5 四階類Bernstein-Bézier曲面
6 結束語
通過提高多項式的次數, 本文首先對三角域上的二次Bernstein-Bézier基函數進行推廣, 然后借助遞推公式對三角域上任意次的Bernstein-Bézier基函數進行推廣。新的基函數具有Bernstein-Bézier基函數的非負性、規范性、對稱性等諸多良好性質, 又因為新的基函數中含有參數, 所以由之定義的新的三角域曲面在具備普通Bernstein-Bézier曲面的凸包性、仿射不變性、角點插值性等優良性質的同時, 又具備了形狀可調性。要想改變新曲面的形狀, 只需簡單地改變形狀參數的值即可。形狀參數越大, 曲面越逼近控制網格, 形狀參數的這一直觀的幾何意義可以幫助我們快速確定合適的參數值來得到想要的形狀。
雖然本文提出的類Bernstein-Bézier曲面具備很多優點, 但由于單一的曲面片難以表示復雜的形狀, 所以為了使新曲面能更好地服務于工程實際, 研究該曲面間的光滑拼接條件迫在眉睫, 而這也正是下一步的研究內容。
[1] Wang Wen-tao, Wang Guo-zhao. Bézier curves with shape parameter [J]. Journal of Zhejiang University:Science A, 2005, 6(6):497-501.
[2] Wu Xiao-qin. Bézier curve with shape parameter [J]. Journal of Image and Graphics, 2006, 11(2):269-274. (in Chinese)
[3] Han Xi-an, Ma Yi-chen, Huang Xi-li. A novel generalization of Bézier curve and surface [J]. Journal of Computational and Applied Mathematics, 2008, 217(1):180-193.
[4] Yan Lan-lan, Liang Jiong-feng. An extension of the Beizer model [J]. Applied Mathematics and Computation, 2011, 218(6):2863-2879.
[5] Wu Hong-yi, Xia Cheng-lin. Extensions of Bézier curves and surfaces with multiple shape parameters [J]. Journal of Computer-Aided Design & Computer Graphics, 2005, 17(12):2607-2612. (in Chinese)
[6] Cao Juan, Wang Guo-zhao. Extension of the cubic Bernstein-Bézier surfaces over the triangular domain[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(9):1403-1407. (in Chinese)
[7] Yu Li-ping. Extension of Bézier surface with two shape parameters over the triangular domain [J]. College Mathematics, 2008, 24(5):58-62. (in Chinese)
[8] Wu Xiao-qin,Han Xu-li.Bézier triangular patch with a shape parameter[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(11):1735-1740. (in Chinese)
[9] Cao Juan, Wang Guo-zhao. An extention of Bernstein-Bézier surface over the triangular domain [J]. Progress in Natural Science, 2007, 17 (3):352-357.
附中文參考文獻:
[2] 吳曉勤. 帶形狀參數的Bézier曲線[J]. 中國圖象圖形學報, 2006, 11(2):269-274.
[5] 鄔弘毅, 夏成林. 帶多個形狀參數的Bézier曲線與曲面的擴展[J]. 計算機輔助設計與圖形學學報, 2005, 17(12):2607- 2612.
[6] 曹娟, 汪國昭. 三角域上三次Bernstein-Bézier參數曲面的擴展[J]. 計算機輔助設計與圖形學學報, 2006, 18(9):1403- 1407.
[7] 于立萍. 三角域上帶兩個形狀參數的Bézier曲面的擴展[J]. 大學數學, 2008, 24(5):58-62.
[8] 吳曉勤, 韓旭里. 帶有形狀參數的Bézier三角曲面片[J]. 計算機輔助設計與圖形學學報, 2006, 18(11):1735-1740.
YANLan-lan,born in 1982,MS,lecturer,her research interest includes computer aided geometric design.
Bernstein-Béziersurfacewithshapeparameters
YAN Lan-lan
(College of Science,East China Institute of Technology,Fuzhou 344000,China)
Because the surface modeling method over the triangular domain can effectively solve the geometric modeling problem of irregular products, it is widely used in practical engineering. However, due to the particularity and complexity of the structure, there are not many studies on the extension of triangular surface at present. In order to enrich the theory of triangular surface, the paper carries out a specialized research on how to enhance the flexibility of shape representation of triangular surface. Firstly, a set of polynomial basis functions of degree four with one parameter over the triangular domain is constructed, which is an extension of the quadratic Bernstein basis function over the triangular domain. Secondly, based on it, the basis functions of degreen+2 with one parameter is defined by a recursive way, which is an extension of the Bernstein basis function of degreen. Thirdly, based on the new basis function of degreen+2, the triangular surface of ordernis defined. The properties of the basis functions and the surfaces are analyzed. The new surfaces not only have the basic properties of the Bernstein-Bézier surfaces, but also enjoy shape adjustable property.
surface design;shape parameter;triangular domain;Bernstein-Bézier surface
2012-09-20;
:2012-12-21
國家自然科學基金資助項目(11261003)
1007-130X(2014)02-0317-08
TP391.4
:A
10.3969/j.issn.1007-130X.2014.02.021

嚴蘭蘭(1982-),女,湖北浠水人,碩士,講師,研究方向為計算機輔助幾何設計。E-mail:yxh821011@aliyun.com
通信地址:344000 江西省撫州市學府路56號東華理工大學理學院Address:College of Science,East China Institute of Technology,56 Xuefu Rd,Fuzhou 344000,Jiangxi,P.R.China

