利用二次B樣條曲線逼近的圖像壓縮方法*
李軍成
(湖南人文科技學(xué)院數(shù)學(xué)系,湖南 婁底 417000)
利用二次B樣條曲線逼近的圖像壓縮方法*
李軍成
(湖南人文科技學(xué)院數(shù)學(xué)系,湖南 婁底 417000)
提出了一種基于Hilbert掃描和二次B樣條曲線逼近的圖像壓縮方法。首先利用Hilbert掃描曲線將二維數(shù)字圖像轉(zhuǎn)化為一維的灰度序列;然后采用二次B樣條曲線對(duì)數(shù)據(jù)進(jìn)行分段逼近,同時(shí)利用逼近的最大絕對(duì)誤差小于最大允許誤差來確定最終分段;最后對(duì)每段數(shù)據(jù)的逼近參數(shù)進(jìn)行編碼。實(shí)驗(yàn)結(jié)果表明,該方法獲得的壓縮效果較好,且計(jì)算量適中,是一種簡單有效的數(shù)字圖像壓縮方法。
圖像壓縮;二次B樣條曲線;分段逼近;Hilbert掃描
1 引言
圖像數(shù)字化后,其所占的空間通常是很大的,為實(shí)現(xiàn)圖像的有效存儲(chǔ)和傳輸,對(duì)數(shù)字圖像進(jìn)行壓縮處理顯得尤為重要。數(shù)字圖像壓縮,就是通過選用有效的方法,去除或減少圖像中存在的冗余,從而降低圖像的存儲(chǔ)空間要求和傳輸帶寬要求。按照壓縮還原效果是否存在失真,圖像壓縮分為兩類:一類是壓縮后的數(shù)據(jù)可以完全恢復(fù)成原來的圖像,沒有任何信息損失,稱為無損壓縮;另一類是壓縮后的數(shù)據(jù)只能近似恢復(fù)原始圖像,信息有一定的損失,稱為有損壓縮。通常來說,有損壓縮可以獲得更高的壓縮效率。按照實(shí)施編碼支持域的不同,圖像壓縮編碼可分為空域法和頻域法[1]。空域法是直接對(duì)像素空間進(jìn)行操作,減少數(shù)據(jù)在時(shí)間和空間上的相關(guān)性,以達(dá)到壓縮數(shù)據(jù)的目的,如Huffman編碼、差值脈碼調(diào)制DPCM(Differential Pulse Code Modulation)編碼等。而頻域法則是通過正交變換,把分散在原圖像空間的數(shù)據(jù)在新空間中得到集中,并保留包含圖像主要信息的系數(shù),從而達(dá)到壓縮數(shù)據(jù)的目的,如離散余弦變換DCT(Discrete Cosine Transform)編碼、小波變換編碼等。
在對(duì)圖像進(jìn)行壓縮編碼時(shí),無論是采用空域法還是頻域法,其目的都是為了進(jìn)一步提高壓縮比和圖像壓縮質(zhì)量。為此許多學(xué)者開始致力于改進(jìn)傳統(tǒng)的圖像壓縮方法或?qū)ふ倚碌膱D像壓縮方法,比如有學(xué)者利用空間域提出了基于曲線曲面擬合的圖像編碼方法。文獻(xiàn)[2]討論了利用B樣條曲面擬合的圖像編碼方法,其基本思想是先用B樣條曲面擬合圖像的灰度值曲面,再對(duì)B樣條參數(shù)進(jìn)行編碼,以此提高壓縮比和改進(jìn)恢復(fù)后圖像的質(zhì)量;文獻(xiàn)[3, 4]提出了一種基于Hilbert掃描和分段局部二次Bernstein多項(xiàng)式逼近的圖像壓縮方法,取得了較好的圖像壓縮效果;文獻(xiàn)[5]提出了將三次Bernstein多項(xiàng)式作為逼近函數(shù)的圖像壓縮方法;文獻(xiàn)[6]針對(duì)交通實(shí)時(shí)路況圖像,提出了一種多項(xiàng)式擬合的圖像壓縮編碼方法,該方法通過對(duì)圖像數(shù)據(jù)的光柵掃描、單調(diào)化處理和多項(xiàng)式擬合系數(shù)保存等三個(gè)步驟來實(shí)現(xiàn)對(duì)圖像數(shù)據(jù)的壓縮;文獻(xiàn)[7]設(shè)計(jì)了一種基于正交多項(xiàng)式分段擬合的圖像壓縮編碼方法,以探索新的圖像壓縮編碼方法;文獻(xiàn)[8]針對(duì)多項(xiàng)式函數(shù)在逼近數(shù)據(jù)時(shí)雖能很好地反映數(shù)據(jù)的漸變性,但不能反映數(shù)據(jù)的突變性這一不足,提出了一種基于Hilbert掃描和二次有理Bézier曲線逼近進(jìn)行圖像壓縮的方法。實(shí)驗(yàn)結(jié)果表明,該方法比傳統(tǒng)的Bernstein多項(xiàng)式逼近方法在圖像的壓縮比和壓縮質(zhì)量方面都有所提高。進(jìn)一步地,文獻(xiàn)[9]又針對(duì)二次有理Bézier曲線在逼近曲線時(shí)不能表示拐點(diǎn)這一缺陷,提出了一種基于擬三次有理Bézier曲線逼近的圖像壓縮方法。
文獻(xiàn)[4, 5]所給出的二次與三次Bernstein多項(xiàng)式逼近方法實(shí)質(zhì)上可看成是相應(yīng)的二次與三次Bézier曲線逼近,利用Bézier曲線逼近進(jìn)行圖像壓縮時(shí),其基本思想是首先將圖像轉(zhuǎn)化為掃描數(shù)據(jù),然后采用分段逼近的方法對(duì)圖像進(jìn)行壓縮編碼。因此,曲線逼近的精度在很大程度上影響著圖像的壓縮比和壓縮質(zhì)量。
文獻(xiàn)[8, 9]提出的基于有理型Bézier曲線逼近的圖像壓縮方法相對(duì)于二次與三次Bézier曲線逼近方法而言,雖然其壓縮比和壓縮質(zhì)量方面都有所提高,但由于采用的是有理函數(shù)進(jìn)行比較,計(jì)算量稍顯偏大。由于Bézier曲線是一種特殊的B樣條曲線,且B樣條曲線比Bézier曲線具有更好的逼近性,因此利用B樣條曲線逼近進(jìn)行圖像壓縮是一種較好的選擇。
為進(jìn)一步減小逼近誤差,提高圖像的壓縮質(zhì)量和減少計(jì)算量,本文提出了一種基于二次B樣條曲線逼近的數(shù)字圖像壓縮方法。該方法首先利用Hilbert曲線掃描[3, 4]將二維形式的數(shù)字圖像轉(zhuǎn)化為一個(gè)一維的灰度數(shù)據(jù)序列,然后采用分段二次B樣條曲線對(duì)數(shù)據(jù)進(jìn)行逼近,最后利用逼近參數(shù)對(duì)圖像進(jìn)行壓縮編碼,從而達(dá)到壓縮圖像的目的。由于彩色圖像可分解成R、G、B三基色圖像,因此下面主要針對(duì)灰度圖像進(jìn)行討論。
2 二次B樣條曲線逼近方法
2.1 二次B樣條曲線
(1)
第二段曲線的表達(dá)式可寫為:
(2)
為方便應(yīng)用,將式(2)重新參數(shù)化,使其參數(shù)t∈[1,2],則式(2)可改寫為:
(3)
于是,整條二次B樣條曲線的表達(dá)式可寫為:
(4)
由式(3)易知:
(5)
(6)
(7)
式(5)~式(7)表明,整條二次B樣條曲線r(t)(1≤t≤2)通過首、末控制點(diǎn)且滿足C1連續(xù)。
由式(4)可得函數(shù)型二次B樣條曲線(簡稱為二次B樣條曲線)的表達(dá)式可寫為:
(8)
式中控制頂點(diǎn)di∈R1(i=0,1,2,3)。
2.2 逼近方法

由于二次B樣條曲線通過首、末控制點(diǎn),故可令d0=V0,d3=Vn,即二次B樣條曲線可寫為:
(9)
于是,只需由給定的數(shù)據(jù)求出控制頂點(diǎn)d1與d2就可實(shí)現(xiàn)二次B樣條曲線對(duì)數(shù)據(jù)Vi(i=0,1,2,…,n)的逼近。
(10)
解得:
(11)
綜合灌漿法:鉆機(jī)對(duì)中調(diào)平固定→開孔鉆至第一段→阻塞洗孔、壓水及灌漿→鉆至終孔段→一次性洗孔、壓水→自下而上分段灌漿至第二段→封孔。
(12)
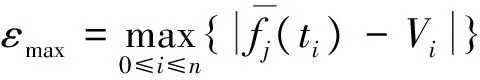
3 圖像壓縮方法
設(shè)某灰度圖像的大小為N×N,首先利用Hilbert掃描將二維形式的數(shù)字圖像轉(zhuǎn)化為一維的灰度值序列,并確定一個(gè)預(yù)分段長度作為分段的基準(zhǔn)值,記為L(一般取為N,N/2,N/4),然后按照每L個(gè)數(shù)據(jù)作為一段將整個(gè)圖像的掃描數(shù)據(jù)預(yù)分為若干段[9, 10]。于是,基于Hilbert掃描與二次B樣條曲線逼近的圖像壓縮方法的步驟為:
Step1將原始圖像通過Hilbert曲線掃描轉(zhuǎn)化為掃描數(shù)據(jù)。
Step2設(shè)置預(yù)分段長度L,對(duì)圖像的掃描數(shù)據(jù)進(jìn)行預(yù)分段。設(shè)定最大允許逼近誤差M。
Step3用二次B樣條曲線去逼近預(yù)分段的一組數(shù)據(jù),并計(jì)算最大絕對(duì)誤差εmax。
Step4如果εmax≤M,則將此段數(shù)據(jù)組成一個(gè)最終分段,轉(zhuǎn)到Step 5;如果εmax>M,則找出絕對(duì)誤差最大的第i個(gè)數(shù)據(jù),然后把前面的i個(gè)數(shù)據(jù)作為一組預(yù)分段數(shù)據(jù),轉(zhuǎn)到Step 3。
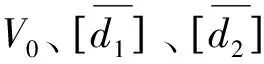
需要注意的是,由于構(gòu)造二次B樣條曲線至少需要4個(gè)數(shù)據(jù)點(diǎn),因此在對(duì)數(shù)據(jù)進(jìn)行分段逼近時(shí),若遇到數(shù)據(jù)個(gè)數(shù)少于4個(gè)的分段則要單獨(dú)考慮。對(duì)于僅有1個(gè)數(shù)據(jù)的分段,其逼近曲線退化為這個(gè)數(shù)據(jù)點(diǎn);僅有2個(gè)數(shù)據(jù)的分段,其逼近曲線退化為連接這2個(gè)數(shù)據(jù)點(diǎn)的直線段;含有3個(gè)數(shù)據(jù)的分段,可將通過這3個(gè)數(shù)據(jù)點(diǎn)的二次曲線作為其逼近曲線。而對(duì)于僅有1個(gè)數(shù)據(jù)的分段,存儲(chǔ)這個(gè)數(shù)據(jù)點(diǎn)即可對(duì)該段進(jìn)行編碼;僅有2個(gè)數(shù)據(jù)的分段,存儲(chǔ)這2個(gè)數(shù)據(jù)即可對(duì)該段進(jìn)行編碼;含有3個(gè)數(shù)據(jù)的分段,存儲(chǔ)其二次曲線的系數(shù)即可對(duì)該段進(jìn)行編碼。
由整個(gè)過程可見,這種圖像壓縮方法是一種有損壓縮。壓縮圖像的精度取決于事先設(shè)定的預(yù)分段長度L和最大允許逼近誤差M。
4 實(shí)驗(yàn)結(jié)果
在PC機(jī)上(CPU:Intel Pentium T4400, RAM:2 GB, OS:WIN7 Basic)通過MATLAB 7.0軟件對(duì)256×256 (8bit) 的Lena圖像進(jìn)行壓縮實(shí)驗(yàn)。
以峰值信噪比(PSNR)和壓縮比(BR)作為壓縮圖像的客觀評(píng)價(jià)指標(biāo),其中PSNR與BR分別定義為:
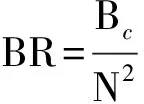
從客觀上看,PSNR越高,圖像的壓縮質(zhì)量越好;BR越小,表明壓縮后圖像的每個(gè)像素所需的比特?cái)?shù)越少,即圖像的壓縮比越高。
當(dāng)預(yù)分段長度L和最大允許誤差M分別取不同值時(shí),本文方法對(duì)Lena圖像進(jìn)行壓縮實(shí)驗(yàn)所得的BR和PSNR如表1所示。
當(dāng)預(yù)分段長度L=64,最大允許逼近誤差M=25時(shí),利用本文方法所得的Lena原圖像與恢復(fù)圖像的對(duì)比如圖1所示,其Hilbert掃描曲線對(duì)比如圖2所示。
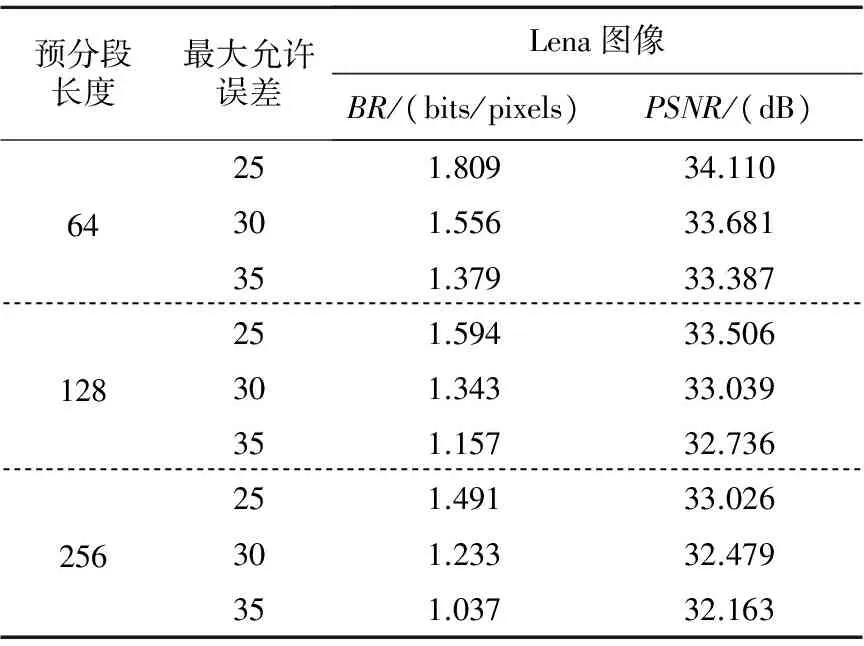
Table 1 Experimental results of Lena imageusing the proposed method表1 本文方法對(duì)Lena圖像的實(shí)驗(yàn)結(jié)果

Figure 1 Compression results contrast of Lena image using the proposed method圖1 本文方法對(duì)Lena圖像的壓縮效果對(duì)比圖

Figure 2 Hilbert curve scanning results contrast of Lena image using the proposed method圖2 本文方法對(duì)Lena圖像的Hilbert掃描曲線對(duì)比圖
為了對(duì)比本文方法與Bézier曲線逼近方法[4, 5]和有理Bézier曲線逼近方法[8, 9]的壓縮結(jié)果,將預(yù)分段長度L都取為256,在給定不同的最大允許誤差時(shí),不同方法對(duì)Lena圖像的實(shí)驗(yàn)對(duì)比結(jié)果如表2所示。
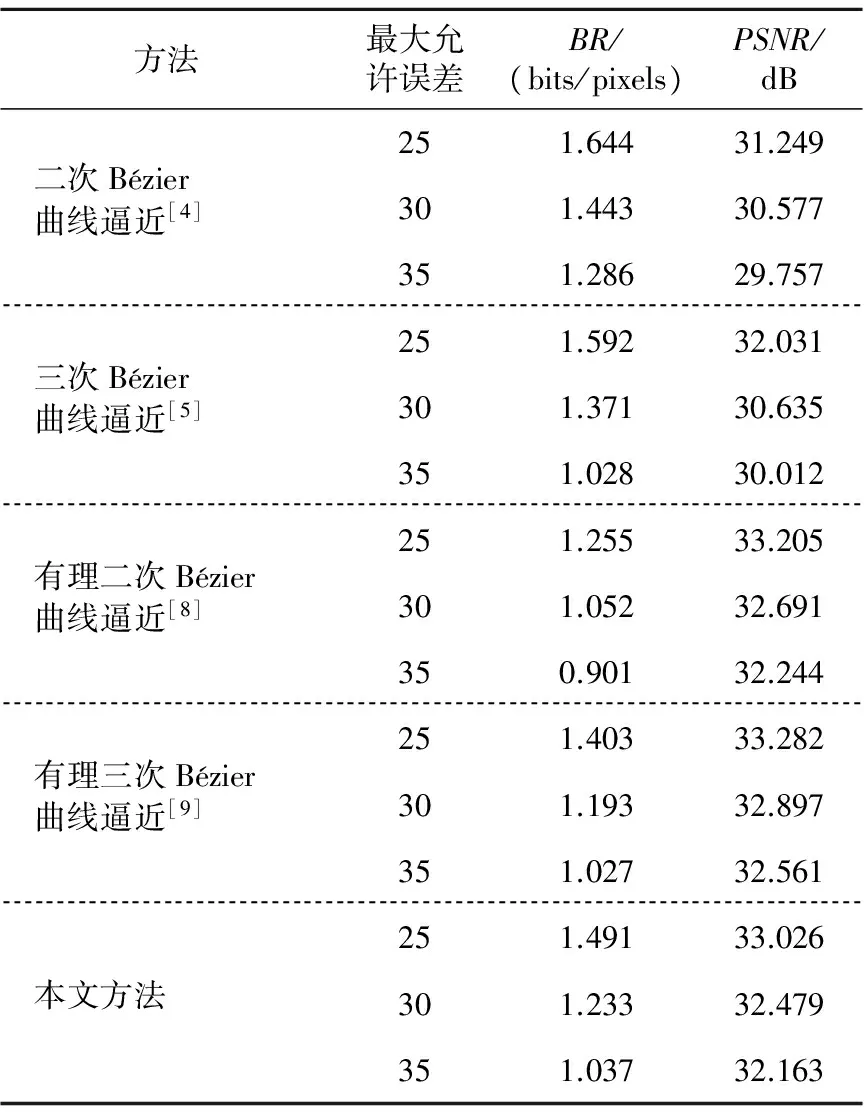
Table 2 Experimental results contrast ofLena image using different methods表2 不同方法對(duì)Lean圖像的實(shí)驗(yàn)結(jié)果對(duì)比
由表2可知,在相同條件下,有理Bézier曲線逼近方法[8, 9]所得的結(jié)果要好于相應(yīng)的Bézier曲線逼近方法[4, 5],且有理三次Bézier曲線逼近方法[9]與有理二次Bézier曲線逼近方法[8]在壓縮比和PSNR方面各占優(yōu)勢(shì);本文方法所得結(jié)果也要好于Bézier曲線逼近方法[4, 5],但比有理Bézier曲線逼近方法[8, 9]稍遜一籌。
分別利用不同方法對(duì)Lena圖像進(jìn)行壓縮實(shí)驗(yàn)(包括編碼與解碼),當(dāng)預(yù)分段長度L都取為256、最大允許誤差M都取為25時(shí),各方法所需的平均時(shí)間如表3所示。
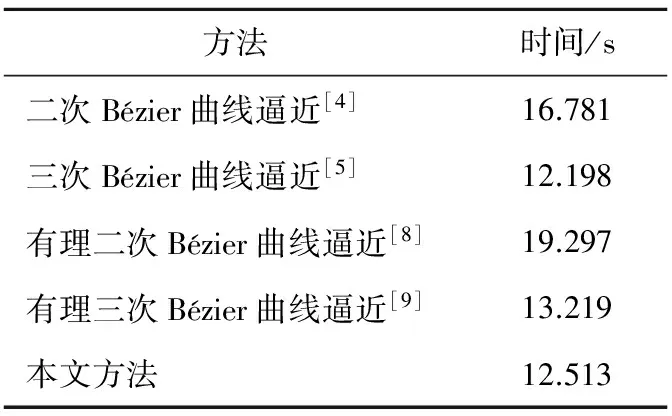
Table 3 Comparison of time using different methods表3 不同方法所需時(shí)間比較
由表3可知,本文方法所需時(shí)間與三次Bézier曲線逼近方法[5]基本相當(dāng),且要少于有理Bézier曲線逼近方法[8, 9]。由此可見,雖然本文方法的壓縮效果要略遜于有理Bézier曲線逼近方法[8, 9],但由于本文方法采用的是多項(xiàng)式函數(shù)逼近,其計(jì)算量明顯要小于采用有理函數(shù)逼近的方法,因此本文方法是一種簡單有效的數(shù)字圖像壓縮方法。
需要說明的是,對(duì)于同一幅圖像,預(yù)分段長度L和最大允許逼近誤差M越大,則圖像的壓縮比越高,但恢復(fù)圖像的PSNR越小,恢復(fù)圖像丟失的細(xì)節(jié)越多。因此,在實(shí)際操作時(shí),要想同時(shí)獲得較高的壓縮比和壓縮質(zhì)量,需根據(jù)所考察圖像的具體情況設(shè)定合理的預(yù)分段長度值和最大允許逼近誤差值。另外,由于本文方法是一種有損壓縮方法,因此相對(duì)于原始圖像而言,解碼后恢復(fù)圖像的質(zhì)量不可避免地會(huì)所有降低,此時(shí)可利用圖像增強(qiáng)或圖像修復(fù)等技術(shù)對(duì)恢復(fù)圖像進(jìn)行再次處理,以獲得質(zhì)量更高的存儲(chǔ)圖像。
5 結(jié)束語
利用曲線逼近方法進(jìn)行圖像壓縮時(shí),逼近誤差對(duì)壓縮圖像的壓縮比和壓縮質(zhì)量有較大的影響。本文提出了一種利用二次B樣條曲線逼近進(jìn)行圖像壓縮的方法,該方法首先通過Hilbert掃描將二維圖像轉(zhuǎn)化為一維灰度序列;然后采用二次B樣條曲線對(duì)數(shù)據(jù)進(jìn)行分段逼近,同時(shí)利用逼近的最大絕對(duì)誤差小于最大允許誤差來確定最終分段;最后對(duì)每段數(shù)據(jù)的逼近參數(shù)進(jìn)行編碼。實(shí)驗(yàn)結(jié)果表明,本文方法能獲得較好的壓縮效果,且計(jì)算量適中,是一種簡單有效的數(shù)字圖像壓縮方法。
[1] Taubman D, Marcellin M. JPEG2000:Image compression fundamentals,standards and practice [M]. Boston, MA:Kluwer, 2001.
[2] Pan J H, Liao Q M. Region coding using improved B-spline surface approximation [J]. Electronics Letters, 2000, 36(2):129-130.
[3] Biswas S. One-dimensional B-B polynomial and Hilbert scan for gray level image coding [J]. Pattern Recognition, 2004, 37(4):789-800.
[4] Biswas S, Lovell B C. Bézier and splines in image processing and machine vision [M]. London:Springer, 2008.
[5] Wang Qiao-long, Wang Zheng-xuan, Xu Zhi-wen, et al. Image compression algorithm based on third degree Bernstein polynomial [J]. Chinese Journal of Scientific Instrument, 2004, 25(S2):432-435. (in Chinese)
[6] Cao Wen-lun,Shi Zhong-ke,Feng Jian-hu.Traffic image coding method based on polynomial approach [J]. Computer Engineering and Applications, 2006, 42(19):183-185. (in Chinese)
[7] Yu Bo,Jian Wei,Chen Jian-xun,et al. A method based on orthogonal polynomial partitioned imitation for image compression coding [J]. Microcomputer Applications, 2007, 28(12):1316-1320. (in Chinese)
[8] Li Jun-cheng, Zhao Dong-biao, Lu Yong-hua. Image compression based on Hilbert scan and quadratic rational Bézier curve approximation [J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(1):21-25. (in Chinese)
[9] Li J C, Zhao D B, Lu Y H. Image compression using Hilbert scan and cubic rational Bézier curve approximation [J]. Journal of Computational Information Systems, 2011, 7(12):4311-4318.
[10] Zhu Xin-xiong. Technology for free curves and surfaces modeling [M]. Beijing:Science Press, 2000. (in Chinese)
附中文參考文獻(xiàn):
[5] 王巧龍, 王鉦旋, 許志聞, 等. 基于三次Bernstein多項(xiàng)式逼
近的數(shù)字圖像壓縮算法[J]. 儀器儀表學(xué)報(bào), 2004, 25(S2):432-435.
[6] 曹文倫, 史忠科, 封建湖.基于多項(xiàng)式擬合的交通圖像編碼方法[J]. 計(jì)算機(jī)工程與應(yīng)用, 2006, 42(19):183-185.
[7] 余波, 簡煒, 陳建勛, 等.基于正交多項(xiàng)式分段擬合的圖像壓縮編碼方法[J]. 微計(jì)算機(jī)應(yīng)用, 2007, 28(12):1316-1320.
[8] 李軍成, 趙東標(biāo), 陸永華. 基于Hilbert掃描與二次有理Bézier曲線逼近的圖像壓縮[J]. 華中科技大學(xué)學(xué)報(bào)(自然科學(xué)版), 2012, 40(1):21-25.
[10] 朱心雄.自由曲線曲面造型技術(shù)[M]. 北京:科學(xué)出版社, 2000.
LIJun-cheng,born in 1982,PhD,lecturer,CCF member(E200012001M),his research interests include computer aided geometric design, geometric modeling, and image processing.
ImagecompressionusingquadraticB-splinecurveapproximation
LI Jun-cheng
(Department of Mathematics,Hunan Institute of Humanities,Science and Technology,Loudi 417000,China)
A method for image compression, based on Hilbert scan and quadratic B-spline curve approximation, is proposed. Firstly, the two-dimensional digital image is converted to one-dimensional grayscale sequence by using Hilbert scanning. Secondly, piecewise quadratic B-spline curves are used to approximate the scanning data, while the condition that the approximate maximum absolute error is less than the maximum allowable error is used to determine the final section. Finally, the approximate parameters of each section are coded. Experimental results show that the proposed method has better compression effect and moderate amount of calculation, which is a simple and effective method for digital image compression.
image compression;quadratic B-spline curve;piecewise approximation;Hilbert scanning
2012-08-13;
:2012-11-30
湖南省自然科學(xué)基金資助項(xiàng)目(13JJ6081);湖南人文科技學(xué)院省級(jí)重點(diǎn)建設(shè)學(xué)科“計(jì)算機(jī)應(yīng)用技術(shù)”資助
1007-130X(2014)02-0325-06
TP391.41
:A
10.3969/j.issn.1007-130X.2014.02.022

李軍成(1982-),男,湖北漢川人,博士生,講師,CCF會(huì)員(E200012001M),研究方向?yàn)橛?jì)算機(jī)輔助幾何設(shè)計(jì)、幾何造型與圖像處理。E-mail:lijuncheng82@126.com
通信地址:417000 湖南省婁底市湖南人文科技學(xué)院數(shù)學(xué)系A(chǔ)ddress:Department of Mathematics, Hunan Institute of Humanities,Science and Technology,Loudi 417000,Hunan,P.R.China

