一種求解最小雙費(fèi)用流問題的算法
馬宇斌,謝 政,陳 摯
(國(guó)防科學(xué)技術(shù)大學(xué)理學(xué)院,湖南 長(zhǎng)沙 410073)
一種求解最小雙費(fèi)用流問題的算法
馬宇斌,謝 政,陳 摯
(國(guó)防科學(xué)技術(shù)大學(xué)理學(xué)院,湖南 長(zhǎng)沙 410073)
多目標(biāo)優(yōu)化是網(wǎng)絡(luò)最優(yōu)化的一個(gè)重要子問題。通過實(shí)際應(yīng)用案例,抽象出一種帶容量限制的雙費(fèi)用權(quán)網(wǎng)絡(luò)模型,并由此提出了相應(yīng)的最小雙費(fèi)用流問題。之后,借鑒網(wǎng)絡(luò)分層的思想,根據(jù)雙費(fèi)用權(quán)網(wǎng)絡(luò)的特點(diǎn)設(shè)計(jì)出一個(gè)求解該問題的雙層原始對(duì)偶算法,并嚴(yán)謹(jǐn)?shù)刈C明了算法的正確性,估計(jì)出算法的復(fù)雜度為O(n2v0)。此外,對(duì)算法進(jìn)行了推廣改進(jìn),使其能求解一般k費(fèi)用權(quán)網(wǎng)絡(luò)中的最小k費(fèi)用流問題。最后,通過一個(gè)實(shí)例來演示算法的執(zhí)行。
雙費(fèi)用權(quán)網(wǎng)絡(luò);最小雙費(fèi)用流;雙層原始對(duì)偶算法;復(fù)雜度
1 引言
網(wǎng)絡(luò)多目標(biāo)優(yōu)化問題作為組合最優(yōu)化和網(wǎng)絡(luò)圖論的一個(gè)交叉問題,一直以來在工程規(guī)劃、地理信息系統(tǒng)、通信網(wǎng)絡(luò)和交通運(yùn)輸?shù)阮I(lǐng)域有著十分廣泛的應(yīng)用。尤其是近年來,隨著通信和航天技術(shù)的發(fā)展,各國(guó)都在大力研發(fā)天基信息網(wǎng)絡(luò)系統(tǒng),以爭(zhēng)取在海、陸、空、天等領(lǐng)域取得自主控制權(quán);而對(duì)天基信息網(wǎng)絡(luò)的研究歸根到底就是求解一個(gè)多權(quán)網(wǎng)絡(luò)最優(yōu)化問題,其求解目標(biāo)會(huì)因研究側(cè)重點(diǎn)或分析方法的不同而不同。若將網(wǎng)絡(luò)鏈路上的信息通行代價(jià)和丟包率這兩個(gè)重要參數(shù)看成是特殊的“費(fèi)用”,再輔以鏈路帶寬約束,則問題就變成一個(gè)帶容量限制的雙費(fèi)用權(quán)問題。對(duì)于雙費(fèi)用權(quán)問題,傳統(tǒng)的網(wǎng)絡(luò)流算法[1~4]已經(jīng)不再奏效。王煥雄等[5]從不同角度討論了含有弧容量和弧費(fèi)用的雙權(quán)有向網(wǎng)絡(luò),給出了計(jì)算兩個(gè)節(jié)點(diǎn)間的使費(fèi)用與容量之比最小的路徑的多項(xiàng)式算法,但這種“雙權(quán)”包括了容量,實(shí)質(zhì)仍是單費(fèi)用網(wǎng)絡(luò);Zhu De-tong[6]針對(duì)廣義多品種最小費(fèi)用流問題,提出一種對(duì)偶理論,將問題轉(zhuǎn)化成一對(duì)含有內(nèi)、外層問題的雙水平規(guī)劃,并導(dǎo)出相應(yīng)的Kuhn-Tucker條件,但未給出具體算法及復(fù)雜性分析;孫小軍等[7]提出了單費(fèi)用運(yùn)輸網(wǎng)絡(luò)中的最少時(shí)間最小費(fèi)用路問題,即要求找出通行時(shí)間最短的最小費(fèi)用路,并給出了一個(gè)求解算法;Coello[8]于2006年針對(duì)雙目標(biāo)綜合優(yōu)化問題提出了基于計(jì)算效率的進(jìn)化算法,使運(yùn)算時(shí)間大幅下降,但在理論上無法保證算法收斂;敖友云等[9]對(duì)綜合優(yōu)化問題提出了一種差分進(jìn)化算法,通過引進(jìn)Paretoε-支配關(guān)系來控制進(jìn)化策略和參數(shù)范圍,提高了求解的成功率;吳潤(rùn)秀[10]對(duì)雙權(quán)網(wǎng)絡(luò)最優(yōu)化求解提出一種基于粒計(jì)算的分層算法,通過將雙權(quán)復(fù)雜網(wǎng)絡(luò)映射成一個(gè)分層網(wǎng)絡(luò),得到數(shù)據(jù)分布優(yōu)化的滿意解。
本文在對(duì)帶容量限制的網(wǎng)絡(luò)雙費(fèi)用權(quán)問題進(jìn)行分析和探討的基礎(chǔ)上,結(jié)合文獻(xiàn)[6]和原始對(duì)偶算法的思想,針對(duì)雙費(fèi)用權(quán)分主次的情況,提出了一種能有效求解此類最小雙費(fèi)用流問題的算法。
2 數(shù)學(xué)模型建立
對(duì)于天基信息網(wǎng)絡(luò),如果把衛(wèi)星抽象成節(jié)點(diǎn),把星際鏈路抽象成有向弧,將信息通行代價(jià)記為主單位費(fèi)用w1,將丟包率記為次單位費(fèi)用w2,那么該實(shí)際問題可以抽象成以下一般的數(shù)學(xué)網(wǎng)絡(luò)模型,本文稱之為最小雙費(fèi)用流問題:
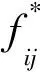
其中,{fij}為關(guān)于w1的最小費(fèi)用流,即{fij}為下面線性規(guī)劃模型的最優(yōu)解:
由于最小雙費(fèi)用流問題涉及兩個(gè)費(fèi)用權(quán)w1和w2,因此也稱之為最小(w1,w2)費(fèi)用流問題。本文將重點(diǎn)研究求解最小雙費(fèi)用流問題的方法,并提出一種雙層原始對(duì)偶算法。
在本文中所使用的概念和記號(hào)除特別聲明外,均見文獻(xiàn)[1]。另外,不失一般性,假設(shè)文中所涉及的網(wǎng)絡(luò)均是簡(jiǎn)單的。
3 雙層原始對(duì)偶算法
3.1 預(yù)備知識(shí)
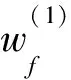
由假設(shè)知,D是簡(jiǎn)單網(wǎng)絡(luò),即D中任意一對(duì)節(jié)點(diǎn)間只有一條弧,故A+(f)∩A-(f)=?,記A(f)=A+(f)∪A-(f)。并且對(duì)?(vi,vj)∈A(f),令:
其中,k=1,2。
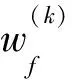
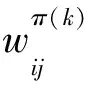
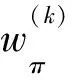
3.2 雙層原始對(duì)偶算法的思想與步驟
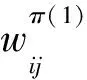
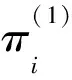
步驟2 若v0=v(f),結(jié)束,f為網(wǎng)絡(luò)D中的最小(w1,w2)費(fèi)用流;否則,轉(zhuǎn)步驟3。
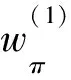
步驟6 沿由步驟5確定的P對(duì)f增廣,其中增廣的流值δ=min{c(P),v0-v(f)},轉(zhuǎn)步驟2。
3.3 算法正確性分析
下面的兩個(gè)定理保證了雙層原始對(duì)偶算法的正確性。
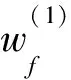
(2)G′(π(2))中任意一條(vs,vt)路都是D(f)中的最小(w1,w2)費(fèi)用路。
證明
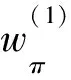
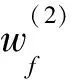
□
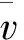

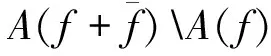
綜上有定理得證。
□
定理3 如果雙費(fèi)用權(quán)網(wǎng)絡(luò)D中存在雙費(fèi)用都可以達(dá)到最小的可行流,那么運(yùn)用雙層原始對(duì)偶算法求出的解必定也是兩種費(fèi)用都達(dá)到最小的。
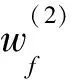
□
事實(shí)上,一旦在一個(gè)雙費(fèi)用權(quán)網(wǎng)絡(luò)中確定了費(fèi)用的主次,即可運(yùn)用上述的雙層原始對(duì)偶算法來求解出最小雙費(fèi)用流及其費(fèi)用值。
3.4 算法復(fù)雜性分析
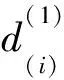
3.5 算法的進(jìn)一步推廣
上文分析的是在帶容量限制的雙費(fèi)用權(quán)網(wǎng)絡(luò)中求解最小雙費(fèi)用流的問題。類似地,如果將問題推廣到帶容量限制的k費(fèi)用權(quán)網(wǎng)絡(luò)中,要求解最小k費(fèi)用流問題,那么只需將上述算法稍作改進(jìn)。首先求出只由第一主費(fèi)用的最小費(fèi)用路構(gòu)成的子網(wǎng)絡(luò)G;然后在G基礎(chǔ)上求出只由第二主費(fèi)用的最小費(fèi)用路構(gòu)成的子網(wǎng)絡(luò)G′,再在G′的基礎(chǔ)上求出只由第三主費(fèi)用的最小費(fèi)用路構(gòu)成的子網(wǎng)絡(luò)G″…,依此類推,一直求到由第k主費(fèi)用的最小費(fèi)用路構(gòu)成的子網(wǎng)絡(luò)G*;最后將流值沿G*上的(vs,vt)路增廣到v0即可。可以看到,本文的算法具有巨大的應(yīng)用價(jià)值。
4 算例
求解圖1所示網(wǎng)絡(luò)D中流值為6的最小雙費(fèi)用流。其中每條弧旁三個(gè)參數(shù)由前往后分別是弧容量、主單位費(fèi)用和次單位費(fèi)用。
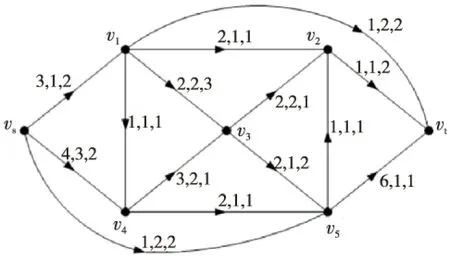
Figure 1 Netwok D圖1 網(wǎng)絡(luò)D
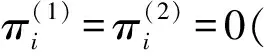
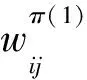
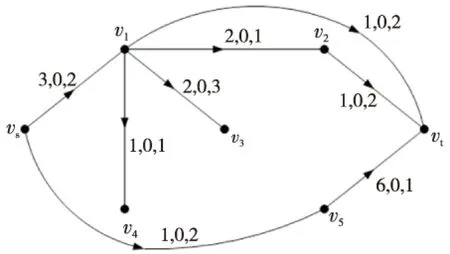
Figure 2 D′(f,π(1))圖2 D′(f,π(1))
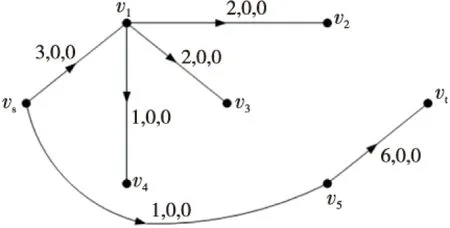
Figure 3 G′(π(2)) before augmentation圖3 未增廣時(shí)的G′(π(2))
接下來,類似地重復(fù)上述操作計(jì)算。由于G′(π(2))每條弧的參數(shù)中主單位費(fèi)用和次單位費(fèi)用均為0,為簡(jiǎn)便起見,在后面的作圖中對(duì)圖G′(π(2))的弧的參數(shù)只保留弧容量一項(xiàng)。
分別求出D′(f,π(1))和G′(π(2)),G′(π(2))如圖4所示,可找到增廣路P=vsv1vt,沿其增廣流值1,此時(shí),v(f)=2<6,返回步驟2繼續(xù)執(zhí)行算法;再次分別求出D′(f,π(1))和G′(π(2)),G′(π(2))如圖5所示,可找到增廣路P=vsv1v2vt,沿其增廣流值1,此時(shí),v(f)=3<6,返回步驟2繼續(xù)執(zhí)行算法。
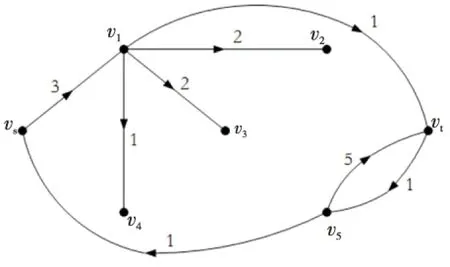
Figure 4 G′(π(2)) after the 1st augmentation圖4 增廣1次后的G′(π(2))
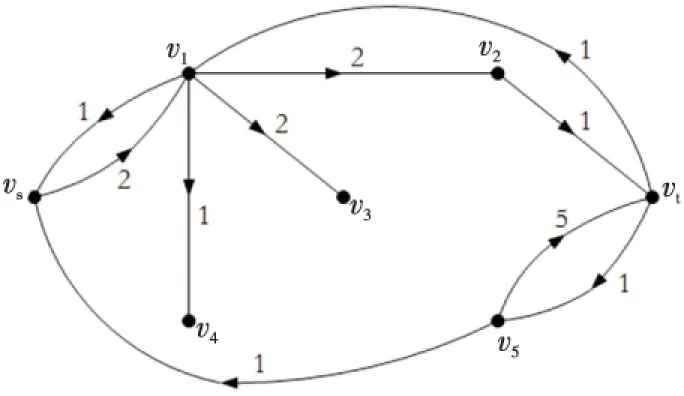
Figure 5 G′(π(2)) after the 2nd augmentation圖5 增廣2次后的G′(π(2))
分別求出D′(f,π(1))和G′(π(2)),G′(π(2))如圖6所示,可找到增廣路P=vsv1v4v5vt,沿其增廣流值1,此時(shí),v(f)=4<6,返回步驟2繼續(xù)執(zhí)行算法;繼續(xù)分別求出D′(f,π(1))和G′(π(2)),G′(π(2))如圖7所示,可找到增廣路P=vsv4v5vt,沿其增廣流值1,此時(shí),v(f)=5<6,返回步驟2繼續(xù)執(zhí)行算法。
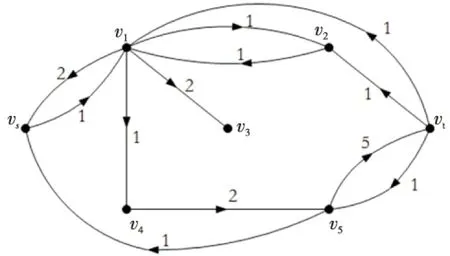
Figure 6 G′(π(2)) after the 3rd augmentation圖6 增廣3次后的G′(π(2))
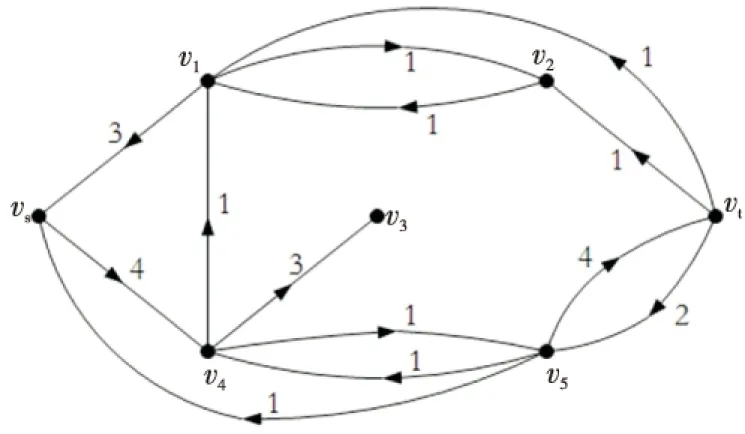
Figure 7 G′(π(2)) after the 4th augmentation圖7 增廣4次后的G′(π(2))
再次分別求出D′(f,π(1))和G′(π(2)),G′(π(2))如圖8所示,可找到增廣路P=vsv4v3v5vt,沿其增廣流值1,此時(shí),v(f)=6,算法結(jié)束,所求得的可行流f為最小雙費(fèi)用流,如圖9所示。
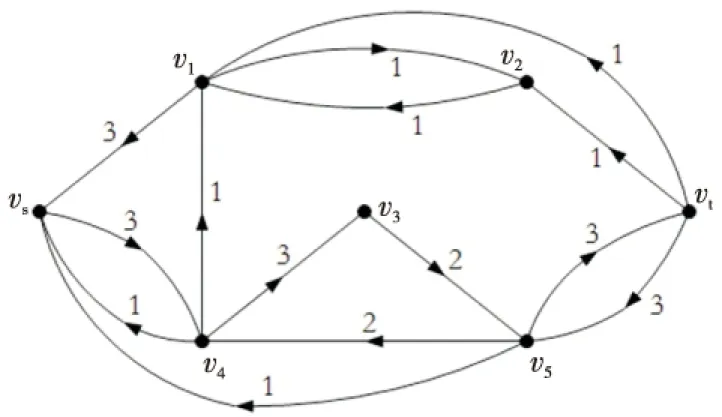
Figure 8 G′(π(2)) after the 5th augmentation圖8 增廣5次后的G′(π(2))
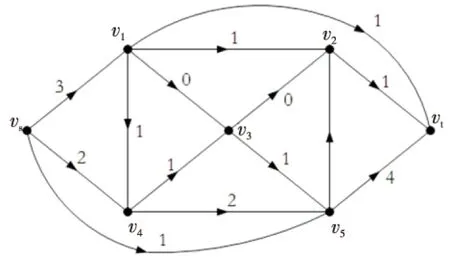
Figure 9 Flow scheme of f圖9 流f的流方案
5 結(jié)束語
本文在了解多目標(biāo)優(yōu)化問題研究現(xiàn)狀的前提下,通過對(duì)時(shí)下熱點(diǎn)天基信息網(wǎng)絡(luò)路由的討論分析,抽象出含主次雙費(fèi)用的雙費(fèi)用權(quán)網(wǎng)絡(luò)和相應(yīng)最小雙費(fèi)用流問題的模型,給出了其線性規(guī)劃形式,并給出了一種雙層原始對(duì)偶算法,巧妙地解決了最小雙費(fèi)用流問題。之后證明了算法的正確性,分析結(jié)果說明算法擁有令人滿意的復(fù)雜度。本文對(duì)算法的改進(jìn)推廣使其能求解一般多費(fèi)用權(quán)網(wǎng)絡(luò)的最小多費(fèi)用流問題。最后的例子演示表明,算法的執(zhí)行是行之有效的。
[1] Xie Zheng, Li Jiang-ping. Network algorithms and complexity theory[M]. 2nd edition. Changsha:National University of Defense Technology Press, 2003.(in Chinese)
[2] Klein M. A primal method for minimal cost flows with applications to the assignment and transportation problems[J]. Management Science, 1967, 14(3):205-220.
[3] Edmonds J, Karp R M. Theoretical improvements in algorithmic efficiency for network flow problems[J]. Journal of the ACM, 1972, 19(2):248-264.
[4] Ahuja R K, Magnanti T L, Orlin J B. Network flows:Theory, algorithms, and applications[M]. London:Prentice Hall, 1993.
[5] Wang Huan-xiong, Li Xi-jun. Optimal analysis of the path of the network with double weights[J]. Journal of Jilin Institute of Chemical Technology, 2001, 18(2):64-66.(in Chinese)
[6] Zhu De-tong. Dual theories of general multicommodity minimal cost flow problems[J]. OR Transactions, 2002, 6(3):17-26.
[7] Sun Xiao-jun, Jiao Jian-min. An algorithm for the problem of finding the minimal-cost path with the minimal time[J]. Computer Engineering & Science, 2008, 30(7):77-78.(in Chinese)
[8] Coello Coello C A. Evolutionary multiobjective optimization:A historical view of the field[J]. IEEE Computational Intelligence Magazine, 2006, 1(1):28-36.
[9] Ao You-yun, Chi Hong-qin. Differential evolution algorithm for multi-objective optimization[J]. Computer Engineering & Science, 2011, 33(9):88-94.(in Chinese)
[10] Wu Run-xiu. Double weighted hierarchical network algorithm based on granular computing[J]. Computer Engineering and Applications, 2011, 47(24):77-87.(in Chinese)
附中文參考文獻(xiàn):
[1] 謝政,李建平. 網(wǎng)絡(luò)算法與復(fù)雜性理論[M].第二版. 長(zhǎng)沙:國(guó)防科技大學(xué)出版社, 2003.
[5] 王煥雄, 李喜軍. 雙權(quán)網(wǎng)絡(luò)路徑的最優(yōu)化分析[J]. 吉林化工學(xué)院學(xué)報(bào), 2001, 18(2):64-66.
[7] 孫小軍, 焦建民. 一種求解最少時(shí)間最小費(fèi)用路問題的算法[J]. 計(jì)算機(jī)工程與科學(xué), 2008, 30(7):77-78.
[9] 敖友云, 遲洪欽. 多目標(biāo)優(yōu)化差分進(jìn)化算法[J]. 計(jì)算機(jī)工程與科學(xué), 2011, 33(9):88-94.
[10] 吳潤(rùn)秀. 基于粒計(jì)算的雙權(quán)網(wǎng)絡(luò)分層算法[J]. 計(jì)算機(jī)工程與應(yīng)用, 2011, 47(24):77-87.
MA Yu-bin,born in 1988,MS candidate,his research interest includes network optimization.

謝政(1960-),男,湖南衡陽人,教授,研究方向?yàn)榻M合最優(yōu)化。E-mail:xiezheng@nudt.edu.cn
XIE Zheng,born in 1960,professor,his research interest includes combination optimization.

陳摯(1965-),男,湖南湘鄉(xiāng)人,碩士,副教授,研究方向?yàn)榻M合最優(yōu)化。E-mail:chenzhi@nudt.edu.cn
CHEN Zhi,born in 1965,MS,associate professor,his research interest includes combination optimization.
An algorithm to solving minimum double-cost flow problem
MA Yu-bin,XIE Zheng,CHEN Zhi
(College of Science,National University of Defense Technology,Changsha 410073,China)
Multi-objective optimization is a critical part of network optimization. The paper derives a minimum double-cost flow problem in double-cost network model with limitations on capacity from a practical case. According to the thought of hierarchy and the feature of double-cost network, the corresponding minimum double-cost flow problem is introduced and a two-layer primal-dual algorithm is proposed to solve it. The correctness of our algorithm is proved and its complexity is estimated asO(n2v0). Besides, the algorithm is improved to solve the minimumk-cost flow problem ink-cost network. Finally, a case is used to exhibit how the algorithm works.
double-cost network;minimum double-cost flow;two-layer primal-dual algorithm;complexity
2012-06-21;
2012-12-19
1007-130X(2014)03-0446-06
TP301.6
A
10.3969/j.issn.1007-130X.2014.03.012

馬宇斌(1988-),男,廣東臺(tái)山人,碩士生,研究方向?yàn)榫W(wǎng)絡(luò)最優(yōu)化。E-mail:jhun31@126.com
通信地址:410073 湖南省長(zhǎng)沙市國(guó)防科學(xué)技術(shù)大學(xué)理學(xué)院學(xué)員五隊(duì)
Address:Team 5,College of Science,National University of Defense Technology,Changsha 410073,Hunan,P.R.China

