一種航天器有效迎風面積的求解方法

朱戰(zhàn)霞, 裴韶彬, 唐歌實, 李勰, 馬家瑨

(1.西北工業(yè)大學 航天學院, 陜西 西安 710072;2.航天飛行動力學國家重點實驗室, 北京 100094;3.北京航天飛行控制中心, 北京 100094)

0 引言

大氣阻力模型精度是影響軌道確定及預報精度的主要因素之一。對于低軌航天器,大氣阻力模型精度主要取決于大氣密度、阻力系數(shù)以及有效迎風面積的精度。現(xiàn)有大氣密度模型已比較精確并得到了普遍應用,如CIRA系列、DTM系列、Jacchia系列、MSIS系列等[1]。另外,由于軌道環(huán)境中自由分子流假設成立,故可認為在軌航天器的阻力系數(shù)為常數(shù)。因此,有效迎風面積就成為影響大氣阻力模型精度的一個關鍵因素。

目前,大氣阻力建模時,迎風面積通過兩種方式獲得,一種方式認為迎風面積為常值;另一種是將迎風面積作為參數(shù)和軌道參數(shù)一起估計。對于復雜外形且姿軌運動形式變化多樣的航天器,前一種精度太差,后一種不易求解。為此,國內(nèi)外學者提出了一些新方法[2-6],例如基于3DMAX和數(shù)據(jù)擬合技術[2]、B樣條曲線曲面造型和包含互斥理論[3]、各類幾何及拓撲變換模型[4]等新方法,可有效解決計算精度不高的問題,但這些方法以飛機為對象,對于航天器其適用性有待于進一步檢驗。另外,也有學者針對航天器研究了考慮遮擋的投影面積求解問題[5-6],對于較簡單的空間任務,可在一定程度上提高迎風面積的計算精度。但是針對未來復雜操作任務軌道的精確確定及預報,其精度還有待于進一步提高。

為此,本文提出基于微元思想建立航天器網(wǎng)格模型以求解有效迎風面積的方法,并通過結(jié)合Graham’s Scan法和射擊線掃描法,進行航天器各部分輪廓的確定,以實現(xiàn)有效迎風面積的準確求解。

1 航天器三維模型建立

1.1 基于微元劃分思想的三維建模方法

航天器在其速度矢量法平面上的投影,即為有效迎風面積。考慮到飛行過程中的姿態(tài)變化,各部分(例如主體、太陽能帆板、各類載荷等)之間會存在相互遮擋,且當航天器外形復雜、外表面有曲面時,三維建模將無法用較少的節(jié)點確定其形狀和輪廓,導致無法精確求解有效迎風面積。為此,本文引入微元劃分的思想進行航天器三維建模,即把航天器表面劃分為有限個微元,保證有足夠的節(jié)點信息描述各表面特性,以精確確定航天器的形狀和輪廓。建模時,基于Pointwise進行微元網(wǎng)格劃分,利用四邊形網(wǎng)格對航天器各表面進行逼近。

為了便于對航天器各部分獨立處理,本文提出采用分塊建模的思想建立三維網(wǎng)格模型,即在航天器本體坐標系下分別建立航天器主體、太陽能帆板及其他載荷的模型,但各部分模型均可獨立導出。這種網(wǎng)格模型建立方式,使航天器上活動部件的運動(太陽能帆板的旋轉(zhuǎn))能夠獨立描述,同時也使生成的網(wǎng)格模型具有很強的擴展性,并能充分利用已有的網(wǎng)格模型。例如,對于交會對接等任務,若兩航天器各自的網(wǎng)格模型已存在,則只需將其統(tǒng)一在同一坐標系下即可進行后續(xù)計算,可避免重復建模,減小網(wǎng)格建模工作量。

1.2 航天器網(wǎng)格模型在速度矢量法平面內(nèi)的投影

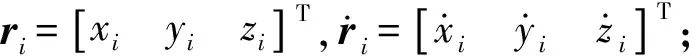
(1)

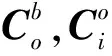
(2)

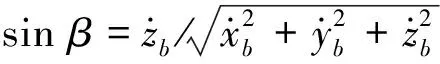
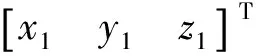
(4)

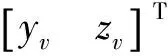
對于航天器三維網(wǎng)格模型上的所有節(jié)點,其在航天器速度坐標系下的投影將構(gòu)成一個點集。針對此點集,進行凸包求解以確定投影輪廓,進一步可求得有效投影面積。

2 航天器有效迎風面積的求解算法

針對航天器運動過程中各部件之間存在遮擋的情況,本文提出基于Graham’s Scan法和射擊線掃描法的有效投影面積求解算法,即采用Graham’s Scan法進行凸包求解以確定投影輪廓,之后采用射擊線掃描法進行有效迎風面積的求解。該方法可有效避免航天器實際飛行時各部分間的遮擋及太陽能帆板的旋轉(zhuǎn)引起的迎風面積重疊,實現(xiàn)有效迎風面積的準確求解[7]。

2.1 航天器各部分投影輪廓的確定

航天器各部分的投影輪廓通過求解網(wǎng)格節(jié)點在速度矢量法平面內(nèi)投影點集的凸包確定。目前,平面點集的凸包求解方法較多,其中最常用的是包裹法及Graham’s Scan法。由于Graham’s Scan法實現(xiàn)簡單、效率高且精度較好,故本文采取此方法進行凸包的求解。Graham’s Scan法是一種試探性增長凸包的方法,其思想如下:

(1)排序:設投影得到的平面點集為Q,在點集Q中,求得縱橫坐標都最小的點作為初始點p0。計算該點和其他各點的連線與橫坐標正向的角度,按從小到大將這些點排序,若有角度相同的情況,優(yōu)先排列最接近p0的點,經(jīng)過排列后,稱它們的對應點為p1,p2,p3,…,pn。

(2)掃描:從初始點開始,凸包上每條相鄰線段的旋轉(zhuǎn)方向應該一致,并與掃描的方向相反。如果發(fā)現(xiàn)新加的點使新線段與上一條線段的旋轉(zhuǎn)方向發(fā)生變化,則可判定上一個點必然不在凸包上。

若航天器某部分網(wǎng)格在投影平面內(nèi)的點集為Q,那么基于以上方法,求解點集Q所對應的凸包,即得到投影輪廓。

2.2 航天器有效迎風面積的確定

航天器有效迎風面積即航天器各部分在速度矢量法平面內(nèi)投影輪廓的并集。基于前面得到的投影輪廓,采用射擊線掃描法,可以求得航天器有效迎風面積。步驟如下:

(1)確定投影平面內(nèi)航天器各部分輪廓點的坐標范圍。找出航天器各部分投影輪廓點的yv坐標的最大值yvmax和最小值yvmin,zv坐標的最大值zvmax和最小值zvmin。

(2)劃分網(wǎng)格確定射擊線。由直線y=yvmax,y=yvmin和z=zvmax,z=zvmin確定其所圍成的平面矩形區(qū)域S。選定yv方向和zv方向的步長分別為Δyv和Δzv,將平面矩形區(qū)域S劃分成面積等于Δyv×Δzv的N個小網(wǎng)格,如圖1所示。在每個網(wǎng)格內(nèi)產(chǎn)生一條垂直于投影平面Oyvzv的射擊線(圖中的黑點),且使各射擊線在投影平面的投影點位于各個小網(wǎng)格的中心,共計N條。

(3)射擊線投影點的掃描判斷。生成N條射擊線后,若投影點在航天器任一部分的投影輪廓內(nèi),則認為該射擊線所在的面積為Δyv×Δzv的小網(wǎng)格屬于航天器各部分投影輪廓的并集區(qū)域。從射擊線1到射擊線N的順序?qū)教炱髟谒俣仁噶糠ㄆ矫鎯?nèi)的投影進行掃描,統(tǒng)計出滿足在航天器任一部分的投影輪廓內(nèi)的射擊線投影點的個數(shù),將其乘以每個小網(wǎng)格的面積(Δyv×Δzv)即可得到總面積St。

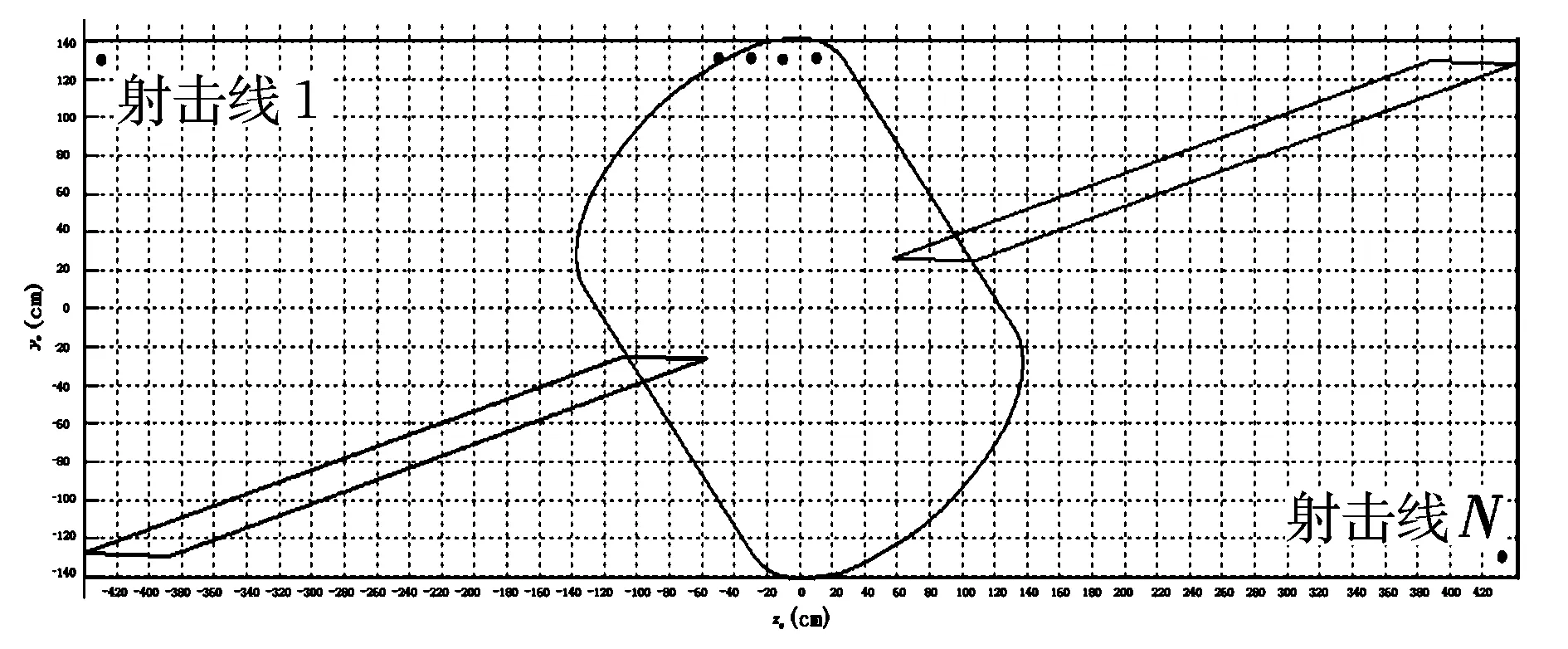
圖1 輪廓點坐標范圍的確定Fig.1 Confirmation of the coordinate scope of points

由于射擊線掃描法是按從射擊線1到射擊線N的順序依次掃過平面矩形區(qū)域S,投影點包含于航天器任一部分的投影輪廓內(nèi)即將該投影點計數(shù),如果射擊線投影點同時在多個部分的投影輪廓內(nèi),說明這幾個部分存在互相遮擋的情況,不再對該投影點進行重復計數(shù),故總面積St就等于航天器的有效迎風面積。因此,該方法有效地解決了傳統(tǒng)方法中有效迎風面積計算時遮擋面積重復計算的問題。

3 算例與分析

為驗證本文方法和算法的合理性與精度,以帶有太陽能帆板的航天器為例,對不同姿態(tài)、不同帆板旋轉(zhuǎn)角度下的有效迎風面積進行求解,并與參考值進行對比分析。給定航天器的外形參數(shù)如下:主體為圓柱體,底面直徑為1 m,高為1 m;太陽能帆板為長方形,長為3 m,寬為1 m,帆板旋轉(zhuǎn)軸通過航天器主體質(zhì)心,與航天器本體坐標系的zb軸平行。

利用前文所述的基于微元劃分思想建立該航天器的三維網(wǎng)格建模,并對主體和太陽能帆板單獨建模。對于主體,各邊節(jié)點均取為20,對于太陽能帆板,用四個頂點坐標表示。最終生成的網(wǎng)格模型如圖2所示。

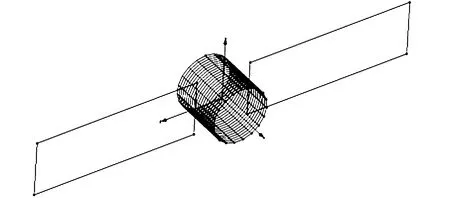
圖2 航天器的網(wǎng)格模型Fig.2 Grid model of spacecraft

基于此模型,利用本文算法進行有效迎風面積的計算。由于航天器需對地定向,故一般飛行過程中只考慮側(cè)滑角,表1給出了幾種典型飛行狀態(tài)下的有效迎風面積計算結(jié)果。表中參考值是通過在pro/e(專用軟件)中建立相應航天器模型由軟件直接給出的。

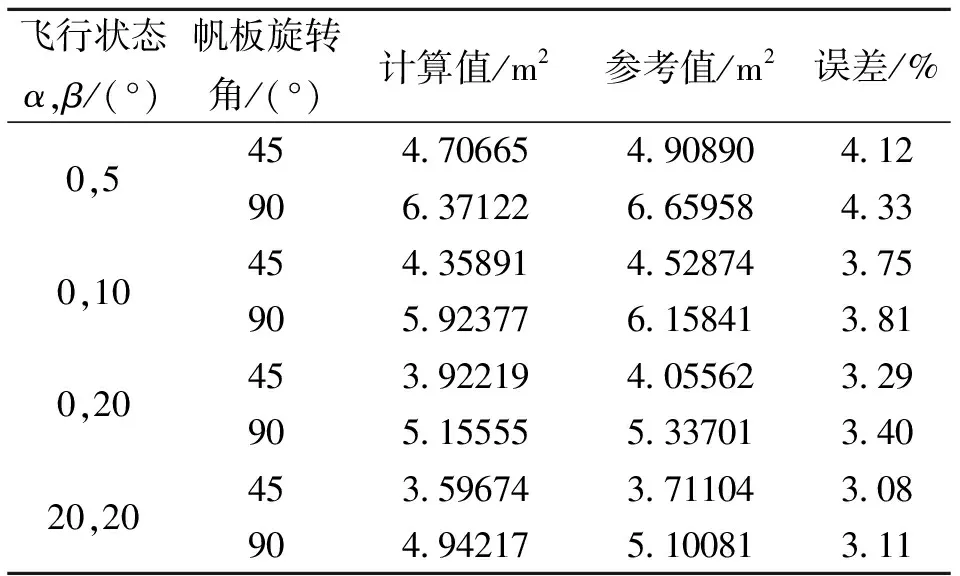
表1 不同飛行狀態(tài)及帆板旋轉(zhuǎn)角下航天器的有效迎風面積計算值及參考值 Table 1 Computed value and theory value of front face area under different flight conditions and sailboard rotating angle

將計算值與參考值比較可知,本文方法所得結(jié)果與參考值的誤差小于5%,說明算法比較合理。

另外,在研究過程中也針對其他飛行情況進行了大量的計算,對結(jié)果統(tǒng)計之后發(fā)現(xiàn),與參考值的誤差均在10%以內(nèi),進一步驗證了算法的合理性和精度。同時還發(fā)現(xiàn),有效迎風面積的計算精度受射擊線個數(shù)影響,射擊線個數(shù)越多,計算精度越高。究其原因在于本文算法中射擊線個數(shù)與網(wǎng)格個數(shù)相同(每個網(wǎng)格內(nèi)產(chǎn)生一條垂直于投影平面的射擊線),射擊線越多,則網(wǎng)格劃分越細,越接近于實際表面形狀和輪廓,因此計算精度越高。建議實際使用中可以適當增加射擊線個數(shù)以提高計算精度。

4 結(jié)束語

復雜外形航天器姿態(tài)變化過程中,有效迎風面積精確求解困難,會影響大氣阻力建模精度。本文基于微元劃分思想建立航天器三維網(wǎng)格模型,采用了分塊建模方法,可獨立描述航天器上不同活動部件,網(wǎng)格模型具有很強的擴展性,且能充分利用已有網(wǎng)格模型實現(xiàn)多載荷系統(tǒng)的快速建模。在此基礎上提出的航天器有效迎風面積求解方法,可解決航天器各部分間存在遮擋、太陽能帆板轉(zhuǎn)動情況下有效迎風面積準確求解的問題。該算法具有工程實用性,可提高低軌航天器大氣阻力模型精度,有利于航天器精細模型的建立。

參考文獻：

[1] AIAA.Guide to reference and standard atmosphere models[M].USA:American Institute of Aeronautics and Astronautics,2010.

[2] 王濤,唐宴虎,簡潔.基于3DMAX的飛機命中面積計算方法[J].火力與指揮控制,2008,33(8):62-68.

[3] 徐元銘,尤偉,王永慶.軍機易損性分析中多重遮擋投影面積計算[J].北京航空航天大學學報,2002,28(2):245-248.

[4] 何光武,張金鐘.飛機武器系統(tǒng)易損性評價中幾何描述研究[J].沈陽航空工業(yè)學院學報,1998,15(2):31-37.

[5] Erwan Mazarico,Zuber Maria T.Improved force modeling on mars-orbiting spacecraft[C]∥AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Honolulu,Hawaii:AIAA,2008.

[6] Erwan Mazarico.Study of the martian upper atmosphere using radio tracking data[D].USA:Massachusetts Institute of Technology, 2008.

[7] 裴韶彬.近地航天器大氣阻力精細建模研究[D].西安:西北工業(yè)大學,2013.