基于多次累加和函數擬合的結構初期沉降預測
劉書斌 周立波 沈 圣 張 浩
(1.無錫地鐵集團有限公司 江蘇無錫 214131;2.福州大學土木學院 福州 350108;3.石家莊鐵道大學土木學院 石家莊 050043)
基于多次累加和函數擬合的結構初期沉降預測
劉書斌1周立波1沈 圣2張 浩3
(1.無錫地鐵集團有限公司 江蘇無錫 214131;2.福州大學土木學院 福州 350108;3.石家莊鐵道大學土木學院 石家莊 050043)
傳統沉降預測方法對于量值小、相對波動大的短期沉降不適用,為此提出適用于結構沉降反復劇烈波動的自修正短期動態預測方法。該方法首先對已獲取的第1~n時刻的結構沉降數據進行多次累加,得到一條單調光滑數據累加曲線,然后對該曲線進行最高(n-1)次多項式擬合,外延得到第(n+1)時刻的沉降預測累加值,再通過回歸遞推,即得到第(n+1)時刻的沉降預測值。同時,對該方法引入“新陳代謝”思想,以更好地反映沉降變化趨勢的目前特征。最后,將某盾構施工現場結構沉降預測值與實測值進行比較。結果表明,該方法能取得較好的預測結果。
城市軌道交通;沉降預測;多次累加;多項式擬合;短期沉降;自修正
我國東部地區以軟土地基為主,大量的工程實踐表明,軟土地基的劇烈擾動(如深基坑開挖,盾構穿越等)都容易使其上結構物產生不同程度的沉降,而劇烈發展且不收斂的初期沉降則會引起結構迅速傾斜乃至倒塌。因此,對擾動區域的結構沉降進行觀測并基于觀測數據對后期沉降的發展做出預報,一直都是保證巖土工程施工和運營安全的重要參考之一。
國內外學者對于沉降已提出不少適用于工程的預測方法,如Peck法、雙曲線法、指數曲線法和Asaoka法等[1-4],近年來學者們還提出了許多基于上述方法的改進方法。但這些方法有一個共同的缺點,即對于量值較大且趨于收斂的后期沉降預測精度較好,而對于量值小、相對波動大的初期沉降預測精度較差。其主要原因有:雙曲線法、指數曲線法假設結構沉降曲線滿足具有單調遞增特性的雙曲線或者指數曲線形式,但只有處于收斂期的后期沉降符合上述假設,結構初期的沉降往往是往復波動的;Peck法、Asaoka法需要預先確定與土體性質相關的計算參數,而結構沉降初期的信息較為貧乏,難以準確獲取這些計算參數的準確值。
針對結構初期沉降具有量值較小、相對波動較大的特點,工程上目前主要采用灰色理論GM(1,1)模型[5],該模型的缺點是使用指數函數來模擬生成數據,要求原始數據服從一定的分布,因而只適用于變形呈指數趨勢變化情況,對在趨勢線上發生跳變的序數據出現異常(如指數偏離過大甚至減小)的情況難以考慮[6]。
針對結構初期沉降預測,筆者提出了一種基于多次累加和多項式擬合的自修正預測方法。與其他預測方法相比,該方法的優點是:這是一種純數學方法,不需要預先確定與土體性質相關的計算參數;該方法不需要假定沉降曲線形式,對于結構初期和后期沉降都適用;該方法適用于貧信息情況,還適于僅有少量初始沉降數據的實際工程預測。
1 基于多次累加和函數擬合的預測
該預測方法分為4個步驟:已知數據累加→曲線擬合→曲線外延→累加值累減。
1.1 已知數據累加
如果已知數據具有明顯的單調簡單光滑函數特征,從理論上說預測值也應該具有這種特征,若直接采用已知數據進行預測,則預測值的準確性較好。但現有沉降數據波動較大,可先將其轉化為具有單調簡單光滑函數特征的數據,下面采用的轉化方法為累加法。
假設已知第1~第n時刻的沉降值序列X(0)=(x(0)(1),x(0)(2),x(0)(3),…,x(0)(n - 1),x(0)(n)),對其進行一次累加,具體做法為

則得到了1-AGO(一次累加)序列X(1)
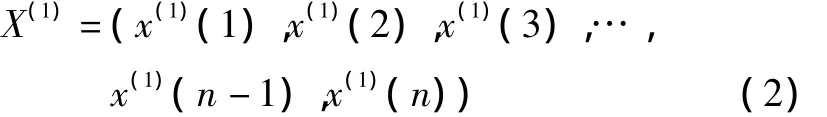
當累加數據形成的曲線具有較好的光滑性時,對其擬合的誤差就比較小。計算序列X(1)的光滑比序列ρ(0)(j)

參照灰色理論 GM(1,1)法[5]的取值,ρ(0)(j)需要滿足以下條件,可認為X(1)滿足光滑性要求

如光滑性條件不滿足,則需要進行多次累加,以使數據序列達到建模所需的單調平滑曲線要求。假定共累加了k次,則得到了k-AGO(k次累加)序列X(k),其中第j次累加的計算公式為

1.2 曲線擬合
得到沉降數據的若干次累加序列后,即可用簡單函數對該序列進行擬合。下面采用多項式擬合,由于有n組數據,可用最高(n-1)次多項式進行擬合。
1.3 曲線外延
得到擬合多項式后,即可外延得到第(n+1)時刻對應的沉降累加值x(k)e(n+1),其中下標e表示該值為外延得到的預測值。
1.4 累加值累減
將沉降累加值做累減處理即可得到第(n+1)時刻的沉降預測值x(0)e(n+1),第j次累減計算公式為

1.5 后續沉降值預測
由于事物發展總是存在一定的連續性以及因果相關性,把未來看成是當前狀態下的延續一般是合理的。則第(n+1)時刻的沉降值總是與第n時刻的沉降值關系較大,與第(n -1),(n -2),…,2,1 時刻的沉降值關系緊密程度則是依次遞減。因此,在預測第(n+2)時刻的沉降值x(0)e(n+2)時,在X(0)序列中剔除第1時刻的實測沉降值x(0)(1),增加第(n+1)時刻的實測沉降值x(0)(n+1);在預測第(n+3)時刻的沉降值x(0)e(n+3)時,在X(0)序列中繼續剔除第2時刻的實測沉降值x(0)(2),增加第(n+2)時刻的實測沉降值x(0)(n+2),后續依次類推,這樣就實現了隨著時間變化沉降預測值的自修正。
另外需要說明的是,使用該方法預測時需要多少前期已知數據(即n的取值),可根據少量后期沉降實測數據試算后比較得出。在多項式擬合時,擬合多項式次數的最佳取值也可根據少量后期沉降實測數據試算得出。
2 模型預測精度及其評價指標
預測精度是指預測值與真實值之間的誤差程度。被廣泛應用的精度指標有:平均絕對百分誤差(MAPE)、絕對誤差平方和(SSE)、相對誤差平方和(SSPE)、標準差(SE)和相對標準差(SPE)等[6]。
假定預測開始后第1時刻到第n時刻沉降預測值為 X*(0)=(x*(0)(1),x*(0)(2),…,x*(0)(n -1),x*(0)(n)),沉降真實值 X(0)=(x(0)(1),x(0)(2),…,x(0)(n-1),x(0)(n)),誤差 e(i)=x*(0)(i)- x(0)(i),則MAPE、SSE、SSPE、SE 和 SPE 的表達式為

顯然,無論采用上述何種指標,指標數值越小表示預測精度越高。下面將用上述指標對該方法的預測精度進行評價。
3 工程應用算例
3.1 工程簡介
某市清水庫為鋼筋混凝土箱型結構,使用年限較長,且底板相對較薄。有地鐵盾構施工下穿該清水庫,為了掌握盾構隧道施工引起地表建筑物沉降的情況,防止底板混凝土開裂,采用靜力水準系統對蓄水池的沉降進行自動化監測。有限元分析及前期現場監測結果均表明,清水庫西南角處靜力水準觀測值及波動幅度最大,為監測系統中最有代表性的靜力水準測點,取該處初期沉降的監測值作為應用案例以評估該方法的適用性。
3.2 沉降預測值與沉降實測值的對比分析
盾構穿越自2013年4月6日起,至4月28日完成,持續23 d,4月6日沉降初值為0。該預測方法于4月8日1:00介入直至項目完成,持續21 d。清水庫西南角沉降值隨著時間推移上下波動,波動周期約為24 h,這說明結構短期沉降變化受到溫度的影響較大。結構在監測期內的沉降變化幅值約為1.3 mm,每天位移波動幅值可達0.4~0.5 mm,波動幅值占整體幅值的30%~40%,因此傳統的預測方法在該項目監測上存在較大困難(見表1)。

表1 本文預測值、GM(1,1)預測值與實測值的比較
選取了4月21日1:00~4月22日1:00 24 h的沉降作為預測對象,采用該方法進行預測,并同時采用GM(1,1)模型作為對比。采用該測點7日晚20:00~24:00的數據作為算例起始序列,其值分別為1.23、1.21、1.18、1.14 和1.11 mm。通過試算,進行2 次累加并采用4次多項式進行擬合即可。表2給出了該方法和GM(1,1)模型得到的預測沉降和實測沉降的對比。根據表1中各預測結果,繪出擬合曲線對比(見圖1)。表2則給出了采用第2節中所列指標對各方法的比較結果。
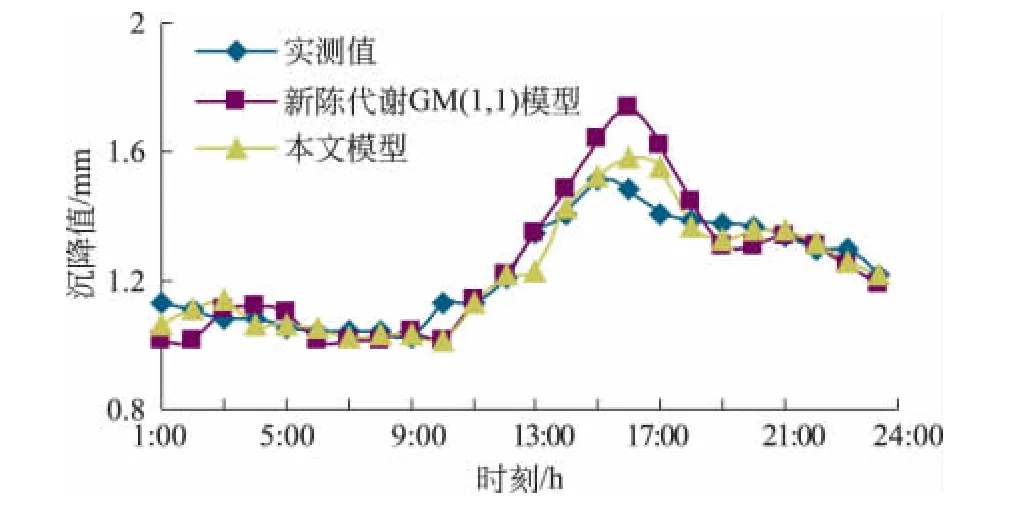
圖1 本文模型預測值、GM(1,1)模型預測值與實測沉降值對比

表2 各預測模型的精度指標值比較
通過圖1可知,受到10:00沉降值的突然上升影響,由于曲線本身具有相關性及慣性,導致該時刻兩種模型的預測誤差都有所增長,由于系統本身具有自修正性,11:00預測誤差迅速減小。但13:00后該方法的預測精度明顯高于GM(1,1),直至17:00兩種方法的預測精度又重新接近,這說明該模型相對于GM(1,1)具有更好的自修正性能,故隨著沉降趨勢的變化,該預測模型能夠快速自我修正,準確預測沉降的發展趨勢,有利于施工單位及時調整方案,對施工具有很強的指導意義。
另外,同時比較表1、圖1和表2所列數據可知,兩種預測模型基本都可以反映沉降整體的發展趨勢,兩者的相關系數都在0.9以上,具有不錯的相關性,但從各類評價指標來看,該模型的預測精度明顯優于GM(1,1)。這說明,相對于目前工程上普遍使用的GM(1,1)方法,該方法具有更好的預測精度和更強的適用性。
4 結語
自修正預測方法通過對源數據的多次累加處理,減少了數據波動對模型帶來的影響,并使用多項式曲線擬合,對曲線未來的發展趨勢做出較好的擬合。通過模型數據的不斷更新,使得模型具備自修正的能力,可適應結構初期沉降具有的量值較小、相對波動較大的特點,且計算快速、簡便。
通過工程實際數據,采用多種理論評價指標對自修正預測方法與GM(1,1)進行比較。比較結果說明,該方法能很好預測結構初期波動較大的沉降,相對于目前工程上普遍使用的GM(1,1)方法,具有更好的預測精度和更強的適用性。該方法對于各種條件相對穩定情況下的沉降值,能夠實現較為精準的預測,對由下部施工及其他環境因素引起的沉降量突變的情況,具有較快的自修正能力,并能及時反應未來沉降的發展趨勢,可為地下隧道的開挖和施工安全提供有力的數據支撐。
[1]Attewell P B,Yeates J,Selby A R.Soil movements induced by tunnelling and their effects on pipelines and structures[M].Glasgow:Blackie,1986:10-50.
[2]龔曉南.高等土力學[M].杭州:浙江大學出版社,1996.
[3]龔曉南,王吉望,于偉堂,等.地基處理手冊[M].2版.北京:中國建筑工業出版社,2000.
[4]Asaoka A.Observational Procedure of Settlement Prediction[J].Soils and Foundations,1978,18(4):87-101.
[5]鄧聚龍.灰色系統基本方法[M].武漢:華中理工大學出版社,1988.
[6]劉思峰,黨耀國,方志耕.灰色系統理論及其應用[M].北京:科學出版社,2004.
Forecasting Method Based on Multi-accumulation and Polynomial Fitting for the Early-stage Structure Settlement
Liu Shubin1Zhou Libo1Shen Sheng2Zhang Hao3
(1.Wuxi Metro Group Co.,Ltd.,Wuxi214131;2.College of Civil Engineering,Fuzhou University,Fuzhou 350108;3.College of Civil Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043)
Abstract:Traditional forecasting methods are proved to be difficult to forecast small and short-term fluctuant settlements in structures.This paper proposed a forecasting method for repeated fluctuant settlements based on multi-accumulation and polynomial fitting.Firstly,it cumulates the observed repeated structural settlements from No.1 to No.n to get a smooth curving data line.Secondly,a maximum n-1 power polynomial fitted function is used for fitting the data line to achieve the forecasting accumulative value on the time of No.n+1.Then the forecasting value on the time No.n+1 can be derived by multi-regressive recursion.Another characteristic of this method is self-correcting forecasting which helps to reflect the change tendency more accurately.At last,a comparison between forecasting and real settlements in a structure near an under-passing subway tunnel construction is carried out.The forecasting value was compared with test value for one shield settlement and the comparing results show that the proposed method can forecast the small and fluctuant settlements with reasonable accuracy.
Key words:urban rail transit;settlement forecasting;multiaccumulation;polynomial fitting;short-time settlement;self-correcting
TU433
A
1672-6073(2014)01-0090-04
10.3969/j.issn.1672-6073.2014.01.022
收稿日期:2013-06-06
2013-07-06
作者簡介:劉書斌,男,大學本科,高級工程師,地下工程與軌道交通方向,從事地鐵、隧道及地下工程領域的設計、施工及咨詢管理工作,zlb00349@wxmetro.net
國家自然科學基金(51208113);河北省自然科學基金(E2013210122);無錫地鐵集團科技項目(2012-353)
(編輯:郝京紅)

