鋰離子電池參數(shù)辨識(shí)與SOC估算研究*

朱 浩，劉云峰，趙 策

(湖南大學(xué) 汽車車身先進(jìn)設(shè)計(jì)制造國(guó)家重點(diǎn)實(shí)驗(yàn)室，湖南 長(zhǎng)沙 410082)

電池的SOC估算精度是影響電動(dòng)汽車性能的重要參數(shù)之一.準(zhǔn)確的電池SOC估計(jì)能夠?yàn)檎嚬β史峙涮峁┮罁?jù)，同時(shí)結(jié)合電池管理系統(tǒng)的軟件，可以優(yōu)化電池的運(yùn)行情況，提高電池的使用壽命.

目前電池SOC估算方法主要有開路電壓法、安時(shí)計(jì)量法、卡爾曼濾波法、神經(jīng)網(wǎng)絡(luò)法以及前面幾種方法的聯(lián)合估算法等[1].開路電壓法需要電池長(zhǎng)期靜置來(lái)測(cè)量開路電壓，不適宜在汽車啟停頻繁時(shí)使用；神經(jīng)網(wǎng)絡(luò)法由于模型復(fù)雜，模型精度依賴于訓(xùn)練數(shù)據(jù)集的完備性，因此還停留于理論研究階段；安時(shí)計(jì)量法是目前主要的電池SOC估算方法，但極易受到SOC初值以及傳感器誤差的影響，使得電池SOC估算精度降低；卡爾曼濾波法采用狀態(tài)空間描述電池所處狀態(tài)，根據(jù)模型輸出與測(cè)量輸出偏差校正電池狀態(tài)，相比經(jīng)典的Wiener濾波法，卡爾曼濾波器具有遞推形式，不需要存儲(chǔ)全部歷史數(shù)據(jù)，易于在計(jì)算機(jī)上實(shí)現(xiàn)，但需要精確的系統(tǒng)模型以及噪聲的統(tǒng)計(jì)特性[2].本文以某國(guó)產(chǎn)三元材料鋰電池包為研究對(duì)象，額定電壓55.5 V，額定容量60 Ah，單體電池額定電壓3.7 V，單體容量30 Ah.基于SAFT公司提出的RC模型，采用多元線性回歸方法辨識(shí)模型參數(shù)，然后采用模糊自適應(yīng)卡爾曼濾波算法估算電池的SOC.

1 RC等效電路模型

圖1所示的電池電路模型是SAFT所提出的.模型包含兩個(gè)電容和3個(gè)電阻，Cb為一個(gè)容量很大的電容，描述電池存儲(chǔ)的容量，Cc為一個(gè)容量相對(duì)較小的電容，主要描述電池的極化現(xiàn)象；Rt為歐姆內(nèi)阻，Re為終止電阻，Rc為容性電阻．它們都是電池SOC的函數(shù).

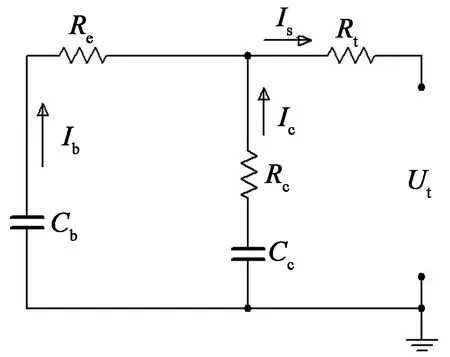
圖1 RC等效電路模型

由圖1所示的電路圖采用基爾霍夫電壓電流定律可求出端電壓的表達(dá)式如式(1)：

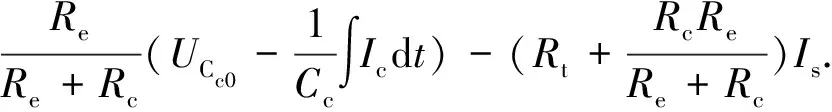
(1)

UCb0和UCc0表示初始時(shí)刻兩個(gè)電容上的電壓，Ib和Ic分別為流過(guò)Re和Rc上的電流，電流方向如圖1所示.

以Cb和Cc上的電壓為狀態(tài)量，端電流Is為輸入量，建立電池的狀態(tài)空間模型如式(2)：

(2)

模型的輸出量為端電壓Ut，輸出方程為：

(3)

2 模型參數(shù)辨識(shí)

為了辨識(shí)電池的模型參數(shù)，采用脈沖放電實(shí)驗(yàn)，得到電池端電壓的脈沖響應(yīng)，根據(jù)得到的數(shù)據(jù)采用多元線性回歸的方法辨識(shí)系統(tǒng)參數(shù).脈沖放電實(shí)驗(yàn)在相等間隔為10%的SOC點(diǎn)之間進(jìn)行，實(shí)驗(yàn)過(guò)程中保持溫度不變，每個(gè)脈沖實(shí)驗(yàn)的間隔時(shí)間為1 h，以讓電池達(dá)到穩(wěn)定狀態(tài).在開始脈沖實(shí)驗(yàn)之前測(cè)量電池的開路電壓，得到對(duì)應(yīng)SOC的開路電壓值.脈沖放電的示意圖如圖2所示，采樣時(shí)間間隔為T=0.05 s，放電電流為60 A，放電時(shí)間持續(xù)18 s，之后將電池靜置90 s，電池端電壓響應(yīng)曲線如圖3所示.

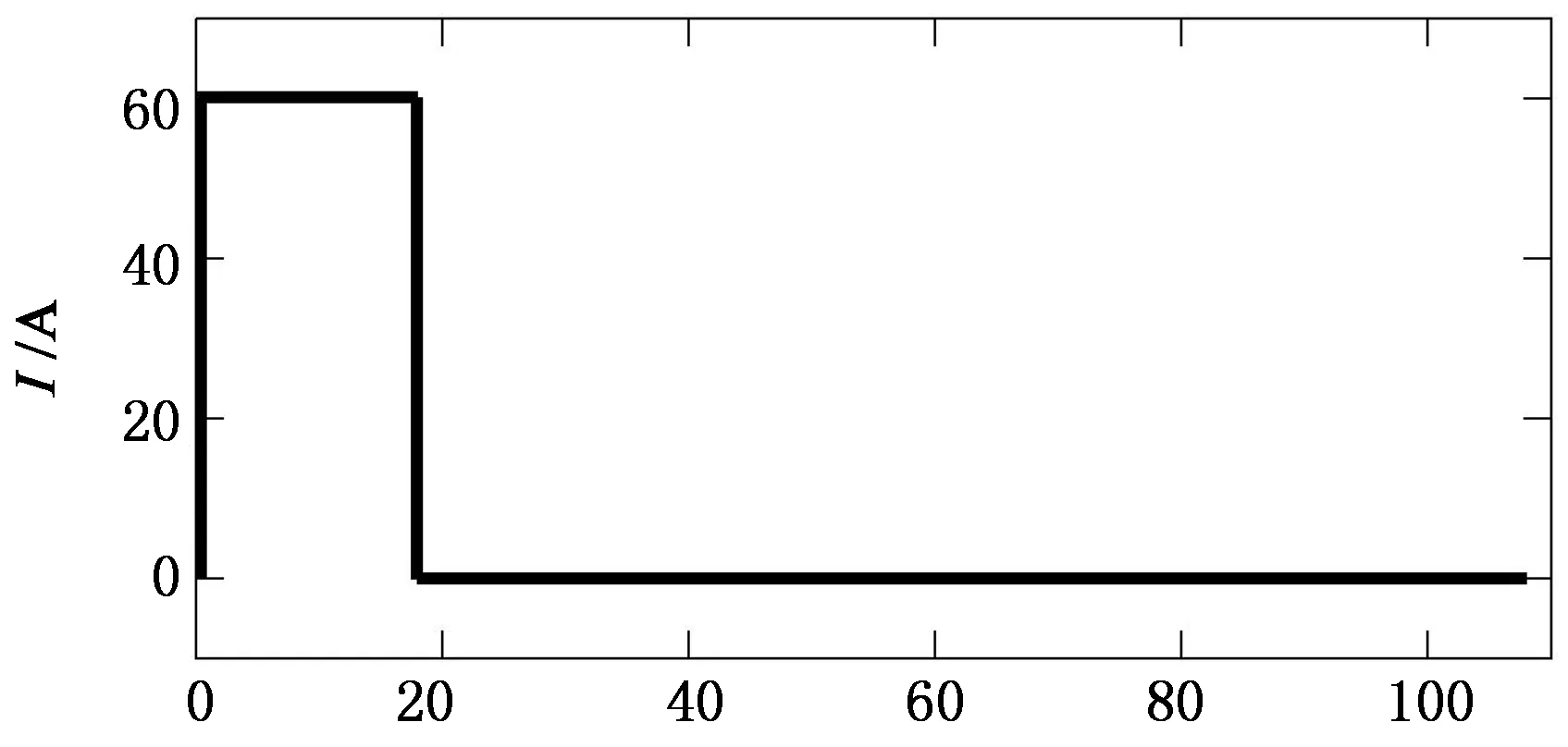
t/s

t/s

根據(jù)實(shí)驗(yàn)獲得的數(shù)據(jù)擬合開路電壓與SOC關(guān)系，通過(guò)觀察各階曲線對(duì)實(shí)驗(yàn)數(shù)據(jù)的擬合效果，最后選取五階曲線作為SOC關(guān)系與開路電壓的函數(shù)關(guān)系式,測(cè)量數(shù)據(jù)與五階擬合曲線的對(duì)比結(jié)果如圖4所示.SOC與開路電壓的表達(dá)式為：

Uocv=-106.73 SOC5+

248.25 SOC4-181.31 SOC3+

34.14 SOC2+17.27 SOC+46.88．

(4)

在每次脈沖放電測(cè)試開始前，電池都經(jīng)過(guò)了一段時(shí)間的靜置，達(dá)到穩(wěn)態(tài)，所以，初始時(shí)刻電容Cb和Cc上的電壓相等，即

UCb0=UCc0=Uinit．

此時(shí)電池的開路電壓等于電容Cb，Cc上的電壓，即Uinit，根據(jù)已知的SOC與開路電壓的關(guān)系可以求得在特定SOC點(diǎn)的Uinit.

以圖1中3個(gè)電阻連線的交叉點(diǎn)作為參考點(diǎn)，應(yīng)用基爾霍夫電壓電流定律，得到如式(5)的方程組：

(5)

化簡(jiǎn)上述方程組得到如式(6)的非齊次微分方程：

(6)

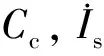
(7)

求解該微分方程，得到Ib，Ic的瞬態(tài)響應(yīng)如式(8)：

Ib=Is(1-Ce-t/τ)．

(8)

在脈沖放電開始后的初始時(shí)刻，電流Ib的大小為：

(9)

根據(jù)初始條件即可解得Ib的瞬態(tài)響應(yīng)為：

Ib=Is(1-ae-t/τ)．

(10)

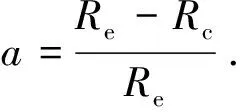
將Ib代入方程組(5)，即可求得Ic的瞬態(tài)響應(yīng)，進(jìn)而將求得的Ib，Ic代入方程(1)，求得端電壓在脈沖放電實(shí)驗(yàn)下的響應(yīng)方程為：

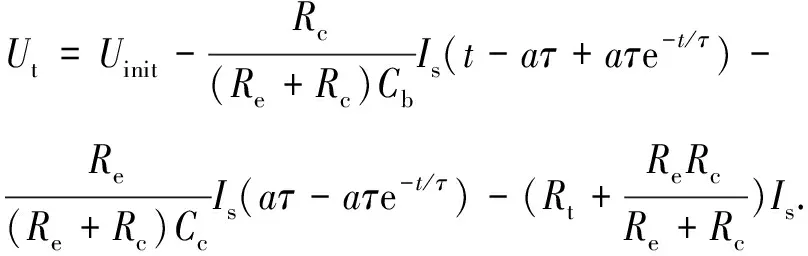
(11)

撤除脈沖電流后，端電壓的響應(yīng)方程為：

(12)

式中：UCb0′，UCc0′表示撤除脈沖電流后，Cb，Cc上的初始電壓．

由式(12)可知，電池端電壓在撤除電流后是一個(gè)緩慢變化的曲線，根據(jù)測(cè)量得到的數(shù)據(jù)采用最小二乘曲線擬合方法即可求得電池的時(shí)間常數(shù)τ.

電池在經(jīng)過(guò)相當(dāng)長(zhǎng)時(shí)間的靜置達(dá)到穩(wěn)定后，電池的端電壓即為電池的開路電壓，由方程(12)可知，穩(wěn)定后的開路電壓為：

(13)

根據(jù)獲得的數(shù)據(jù)對(duì)方程(11)采用多元線性回歸的方法，辨識(shí)電池的模型參數(shù).回歸模型由方程組(14)給定，a1,a2和a3為待辨識(shí)參數(shù).在進(jìn)行參數(shù)辨識(shí)之前，需要假定a值，用多元線性回歸系數(shù)r2來(lái)判定回歸精度，只要超過(guò)0.99即可[3]．

(14)

最后根據(jù)求得的a1，a2和a3，時(shí)間常數(shù)τ以及假定的a計(jì)算電池模型的參數(shù).表1為在25 ℃時(shí)辨識(shí)得到的電池參數(shù)值.

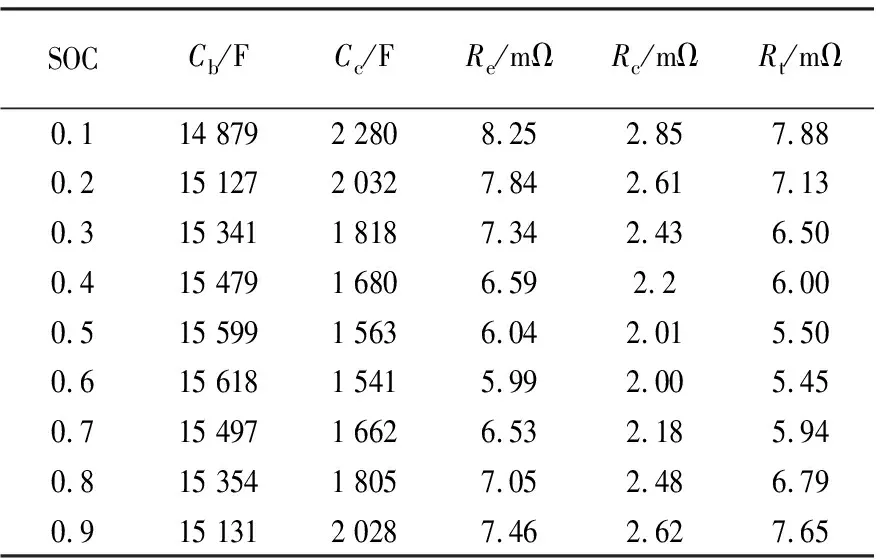
表1 鋰離子電池包等效電路模型參數(shù)

3 電池SOC估計(jì)

對(duì)電池荷電狀態(tài)進(jìn)行估計(jì)，影響估算精度的因素主要是電池模型精度和傳感器所采集信號(hào)的精度.實(shí)際測(cè)量得到的信號(hào)都含有噪聲，需要采用合適的方法濾除噪聲干擾.卡爾曼濾波算法采用最小均方誤差為估計(jì)準(zhǔn)則，在實(shí)際應(yīng)用中需要已知噪聲的統(tǒng)計(jì)特性，實(shí)際信號(hào)中所含噪聲統(tǒng)計(jì)特性往往是未知的，且由傳感器采集信號(hào)中的白噪聲在經(jīng)過(guò)電路放大環(huán)節(jié)后會(huì)改變?cè)肼暤慕y(tǒng)計(jì)特性.因此有必要采用自適應(yīng)卡爾曼濾波，實(shí)時(shí)估計(jì)噪聲的統(tǒng)計(jì)特性，提高電池SOC估算的精度.

由方程(13)可知，通過(guò)實(shí)時(shí)估算電容Cb和Cc上的電壓，就可以知道對(duì)應(yīng)狀態(tài)穩(wěn)定之后的開路電壓，進(jìn)而根據(jù)擬合的開路電壓與SOC的函數(shù)關(guān)系式求得SOC.

以方程(2)，(3)作為自適應(yīng)卡爾曼濾波的狀態(tài)方程和輸出方程，以文獻(xiàn)[4]中的離散化方法將其離散.設(shè)采樣時(shí)間T=0.05 s，輸入量采用零階保持器，并考慮過(guò)程噪聲和測(cè)量噪聲的存在，得到式(15)的狀態(tài)估計(jì)模型：

(15)

系統(tǒng)參數(shù)A，B，C和D的值采用MATLAB中的函數(shù)ss，c2d和ssdata計(jì)算得到.A，B，C和D是SOC的函數(shù)，在不同采樣點(diǎn)上擁有不同的值，在此假定兩個(gè)相鄰采樣點(diǎn)[k，k+1]區(qū)間內(nèi)的系統(tǒng)參數(shù)值A(chǔ)，B，C和D為常數(shù)，采用k時(shí)刻的值.

自適應(yīng)卡爾曼濾波，根據(jù)觀測(cè)得到的數(shù)據(jù)不斷地修正噪聲的統(tǒng)計(jì)特性，以提高濾波精度.Sage和Husa提出了基于觀測(cè)的噪聲統(tǒng)計(jì)極大后驗(yàn)次優(yōu)無(wú)偏估計(jì)器[5]，根據(jù)最新得到的新息更新噪聲統(tǒng)計(jì)特性，更新過(guò)程中賦予每一時(shí)刻的噪聲相同的權(quán)值.文獻(xiàn)[6]提出在更新噪聲統(tǒng)計(jì)特性時(shí)，應(yīng)著重考慮新近數(shù)據(jù)對(duì)噪聲統(tǒng)計(jì)特性的修正作用，采用指數(shù)加權(quán)系數(shù).由于加權(quán)系數(shù)在初始時(shí)刻給予修正量較大的權(quán)值，容易使得濾波器由于突然較大的擾動(dòng)而發(fā)散.為了克服上述缺點(diǎn)，本文采用模糊邏輯自適應(yīng)卡爾曼濾波，通過(guò)監(jiān)測(cè)新息均值和協(xié)方差的變化，對(duì)系統(tǒng)噪聲和觀測(cè)噪聲的權(quán)值進(jìn)行模糊調(diào)節(jié).

狀態(tài)估計(jì)的步驟為：

根據(jù)上一時(shí)刻的狀態(tài)量后驗(yàn)估計(jì)值Xk|k以及當(dāng)前時(shí)刻的輸入量Uk計(jì)算當(dāng)前時(shí)刻狀態(tài)量的先驗(yàn)估計(jì)值Xk+1|k.

Xk+1|k=AXk|k+BUk．

(16)

計(jì)算當(dāng)前時(shí)刻協(xié)方差矩陣的先驗(yàn)估計(jì)值Pk+1|k：

Pk+1|k=APk|kAΤ+ΓQkΓΤ．

(17)

計(jì)算卡爾曼增益Kk+1和殘差RESk+1：

Kk+1=Pk+1|kCΤ(CPk+1|kCΤ+Rk)-1，

(18)

RESk+1=Zk+1-CXk+1|k-DUk+1．

(19)

(20)

對(duì)狀態(tài)量和協(xié)方差更新：

Xk+1|k+1=Xk+1|k+αKkRESk，

(21)

Pk+1|k+1=Pk+1|k-KkCPk+1|k．

(22)

α為增益矩陣的加權(quán)系數(shù)，將式(17)代入式(18)可得：

(23)

由式(23)可知:增益矩陣與系統(tǒng)噪聲和測(cè)量噪聲直接相關(guān).調(diào)整α的值，相當(dāng)于調(diào)整增益矩陣的值，也就相當(dāng)于調(diào)整系統(tǒng)噪聲和測(cè)量噪聲的值，使得系統(tǒng)模型更貼近于實(shí)際模型，提高了濾波精度.

加權(quán)系數(shù)α的值，采用模糊邏輯控制器求得.本文采用Sugeno模糊系統(tǒng)[7]，輸入量是殘差協(xié)方差理論值與實(shí)際值的差值dk+1.

N為一段時(shí)間內(nèi)的統(tǒng)計(jì)次數(shù)，根據(jù)殘差在穩(wěn)態(tài)濾波下的平穩(wěn)遍歷性質(zhì)，其實(shí)際協(xié)方差可以用式(24)進(jìn)行近似[8]:

(24)

殘差的理論協(xié)方差與實(shí)際協(xié)方差的差值dk+1如式(25):

(25)

當(dāng)dk+1等于0時(shí)說(shuō)明正在進(jìn)行最優(yōu)濾波，此時(shí)加權(quán)系數(shù)α應(yīng)為1；當(dāng)dk+1的絕對(duì)值遠(yuǎn)大于0時(shí)，該測(cè)量時(shí)刻的數(shù)據(jù)應(yīng)視為無(wú)效，α應(yīng)取0值，其他情況時(shí)0<α<1.根據(jù)dk+1值的大小，劃分5個(gè)模糊子集，分別為NL(負(fù)大),NS(負(fù)小),Z(零),PS(正小),PL(正大).相應(yīng)的隸屬度函數(shù)如圖5所示.

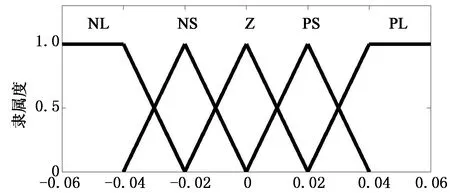
dk+I

模糊邏輯系統(tǒng)的輸出規(guī)則如下：

Ifdk+1isAi,then αi=fi(dk+1);i=1，2，…，M．

Ai表示NL(負(fù)大),NS(負(fù)小),Z(零),PS(正小),PL(正大)中的一種，fi(dk+1)為dk+1的線性函數(shù).M為規(guī)則的條數(shù)，在此M=5.整個(gè)模糊系統(tǒng)的輸出α是各條規(guī)則輸出αi按式(26)加權(quán)平均求得[9].

(26)

其中wi為加權(quán)系數(shù)：

(27)

為了比較模糊自適應(yīng)卡爾曼濾波算法與傳統(tǒng)卡爾曼濾波算法的差異，根據(jù)參數(shù)辨識(shí)得到的電池模型，采用城市道路循環(huán)工況(UDDS)進(jìn)行仿真，初始SOC值設(shè)為0.7.圖6是截取的仿真過(guò)程中通過(guò)實(shí)時(shí)估算Cb,Cc值而計(jì)算得到的電池開路電壓OCV的部分變化曲線，參考曲線表示在沒(méi)有噪聲條件下根據(jù)方程組(15)中的第一個(gè)方程計(jì)算得到的OCV值.根據(jù)估算的OCV值采用方程式(4)可以計(jì)算出仿真過(guò)程的SOC，圖7是截取的仿真過(guò)程中經(jīng)過(guò)放大后的部分SOC值曲線.圖8是整個(gè)仿真過(guò)程中根據(jù)SOC參考值計(jì)算得出的SOC估計(jì)誤差.

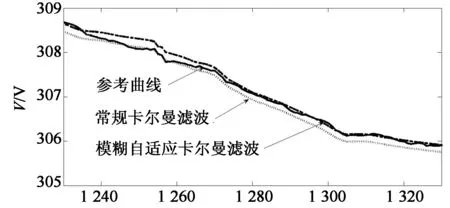
仿真時(shí)間/s

仿真時(shí)間/s

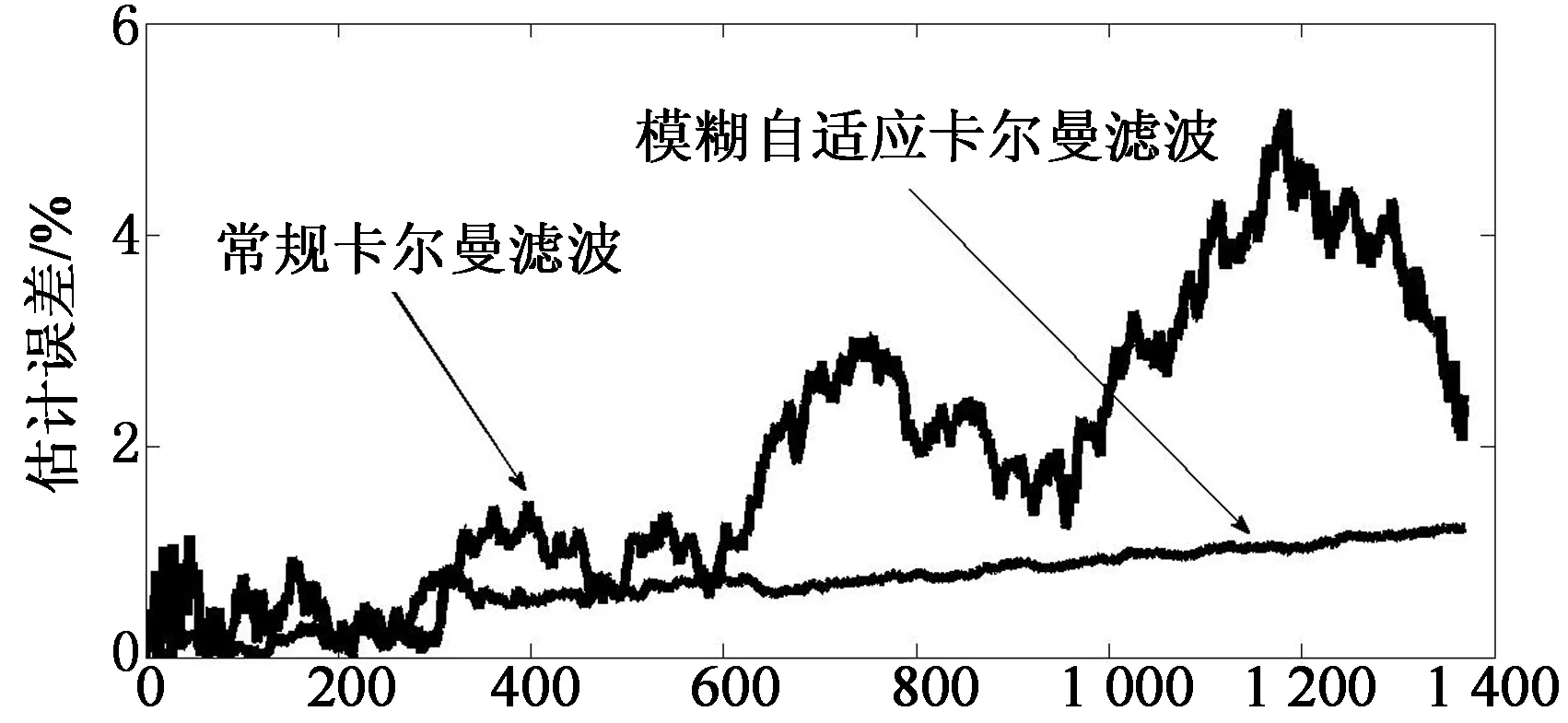
仿真時(shí)間/s

從圖8可以看出，采用模糊邏輯自適應(yīng)卡爾曼濾波的SOC估計(jì)誤差比傳統(tǒng)卡爾曼濾波要小.且濾波誤差增長(zhǎng)較為平穩(wěn)，整體最大誤差不超過(guò)2%，能夠較為準(zhǔn)確地估計(jì)電池的SOC.

4 結(jié) 論

針對(duì)SAFT公司提出的鋰離子電池RC電路模型，提出了采用脈沖放電試驗(yàn)，以實(shí)驗(yàn)數(shù)據(jù)運(yùn)用多元線性回歸來(lái)辨識(shí)電池模型參數(shù)；在運(yùn)用辨識(shí)到的模型估計(jì)電池SOC值時(shí)，采用了模糊自適應(yīng)卡爾曼濾波算法，并與傳統(tǒng)的卡爾曼濾波算法做了對(duì)比，結(jié)果顯示本文提出的模糊自適應(yīng)卡爾曼濾波算法，由于具有自動(dòng)校正模型的功能，相比傳統(tǒng)卡爾曼算法，能夠較為精確地估計(jì)電池的SOC.

[1] 夏朝英，張術(shù)，孫宏濤. 基于推廣卡爾曼濾波算法的SOC估算策略[J]. 電源技術(shù)，2007, 5(2)：414-417.

XIA Chao-ying, ZHANG Shu, SUN Hong-tao. A strategy of estimating state of charge based on extended Kalman filter[J]. Chinese Journal of Power Sources, 2007, 5(2): 414-417.(In Chinese)

[2] WANG J P, GUO J G, DING L. An adaptive Kalman filtering based state of charge combined estimator for electric vehicle battery pack[J]. Energy Conversion and Management, 2009, 50(12):3182-3186.

[3] SANFORD W. Applied linear regression[M]. Hoboken:A John Wiley & Sons, Inc, Publication, 2005：19-32.

[4 ] 張桂香. 計(jì)算機(jī)控制技術(shù)[M]. 長(zhǎng)沙：湖南大學(xué)出版社，2008：86-87.

ZHANG Gui-xiang. Computer control technology[M]. Changsha: Hunan University Press, 2008：86-87.(In Chinese)

[5] SAGE A P, HUSA G W. Adaptive filtering with unknown prior statistics[C]//Proceeding of the Joint American Control Conference. Boulder Colorado: 1969：769-774.

[6] 熊瑞，孫逢春，何洪文. 自適應(yīng)卡爾曼濾波器在車用鋰離子動(dòng)力電池SOC估計(jì)上的應(yīng)用[J]. 高技術(shù)通訊，2012，22(2): 198-204.

XIONG Rui, SUN Feng-chun, HE Hong-wen. State of charge estimation of lithiumion batteries in electric vehicles based on an adaptive extended Kalman filter[J]. High Technology Letters, 2012, 22(2): 198-204.(In Chinese)

[7] TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transaction on SMC, 1985, 15(1): 116-132.

[8] ESCAMILLA-AMBROSIO P J, MORT N. A hybrid Kalman filter-fuzzy logic architecture for multisensor data fusion [C]//Proceeding of 2001 International Conference on Artificial Intel ligence. Mexico City: Intelligent Control．2001：364- 369.

[9] SASIADEK J Z, WANG Q, ZEREMBA M B. Fuzzy adaptive Kalman filtering for INS/GPS data fusion[C]//Proceeding of the 2000 IEEE international Symposium on Rio Patras:Intelligent Control, 2000:181-186.