正交變傳動比面齒輪的設計及三維造型*

林 超，李莎莎，龔 海

(重慶大學 機械傳動國家重點實驗室，重慶 400044)

面齒輪傳動是一種圓錐齒輪與圓柱齒輪相互嚙合的齒輪傳動[1]，圓錐齒輪(面齒輪)采用直齒漸開線齒輪刀具經范成加工而成.常見的面齒輪按傳動位置關系可分為正交、非正交、偏置正交和偏置非正交4種情形[2-5].按照齒形分為直齒面齒輪、斜齒面齒輪和弧齒面齒輪[6-11].目前，相交軸間的變傳動比傳動主要是利用非圓錐齒輪副來實現的[12]，然而非圓錐齒輪副的設計與加工相當困難，正交變傳動比面齒輪副是在深入研究非圓錐齒輪副的基礎上設計的，由一個非圓柱齒輪和特殊非圓錐齒輪(變傳動比面齒輪)組成.與非圓錐齒輪副相比，正交變傳動比面齒輪副的最大特點是設計與加工更簡單，可以利用現有的機床和刀具對其進行加工，易實現批量生產.正交變傳動比面齒輪在紡織機械、農用機械、工程機械、汽車等場合有著廣闊的應用前景，所以對正交變傳動比面齒輪的研究有很重要的理論意義和工程應用價值[13].

正交變傳動比面齒輪目前還無法通過三維軟件對其進行直接造型，而齒輪的三維模型是進行有限元分析、機構仿真、數控加工等不可缺少的，為此，從正交變傳動比面齒輪設計基本原理和插齒加工原理出發，利用VB和Solidworks的二次開發工具，開發一套該面齒輪參數化設計及仿真加工系統，實現快速設計，大大減少重復設計量，縮短設計周期、提高設計效率.正交變傳動比面齒輪仿真加工系統可在計算機上模擬加工過程，得到該面齒輪三維模型并真實、直觀地展現其展成原理、復雜加工過程和效果，為進一步的分析及制造研究奠定基礎.

1 幾何設計

1.1 節曲線設計

本文討論的非圓柱齒輪節曲線為橢圓曲線(包括低階橢圓和高階橢圓)，其節曲線方程為[14]：

(1)

式中:a為橢圓的長軸半徑；k1為橢圓的偏心率，n1為橢圓的階數.

建立正交變傳動比面齒輪副的坐標系如圖1所示：坐標系s1(x1,y1,z1)和s2(x2,y2,z2)為動坐標系分別與非圓柱齒輪和正交變傳動比面齒輪剛性固接.坐標系s10(x10,y10,z10)和s20(x20,y20,z20)為定坐標系，與切齒機床的機座剛性固接.初始時，坐標系s1和s10，s2和s20重合.R為正交變傳動比面齒輪節曲線所在圓柱齒輪的半徑，θ1，θ2分別為非圓齒輪、正交變傳動比面齒輪轉角.

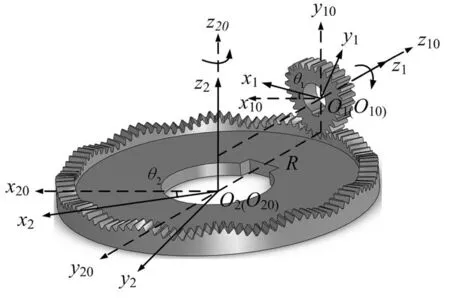
圖1 正交變傳動比面齒輪副設計坐標系

根據空間嚙合原理及空間坐標變換關系得到由s1(x1,y1,z1)轉換到s2(x2,y2,z2)轉換矩陣為：

(2)

根據齒輪嚙合原理的推導，正交變傳動比面齒輪的節曲線在坐標系s2(x2,y2,z2)用下列矩陣方程表示：

(3)

定義n2為正交變傳動比面齒輪的階數，表示該面齒輪節曲線在0～2π范圍內變化的周期個數.根據節曲線封閉的條件有：

(4)

式中：i12為正交變傳動比面齒輪副傳動比.

根據式(1)(4)算得R,帶入式(2)得到正交變傳動比面齒輪節曲線參數方程為：

(5)

由式(3)可以看出，正交變傳動比面齒輪節曲線的x，y坐標表示的是一個半徑為定值R的圓，而z坐標則是隨著θ1變化的，所以正交變傳動比面齒輪的節曲線是圓柱面上的空間曲線.

1.2 齒頂齒根曲線設計

正交變傳動比面齒輪的齒頂高和齒根高沿其節曲線法線方向計算，其齒頂曲線與齒根曲線是節曲線的等距曲線，它們與節曲線之間的法向距離分別是齒頂高ha和齒根高hf.由于直接基于圓柱面求齒頂曲線和齒根曲線的表達式比較困難，將正交變傳動比面齒輪節曲線展開為平面曲線，推導出其齒頂、齒根曲線方程.參照非圓齒輪的齒頂齒根計算方法，得到正交變傳動比面齒輪的齒頂曲線直角坐標表達式：

(6)

齒根曲線直角坐標表達式：

(7)

式中：

1.3 齒面方程

如圖2所示，刀具漸開線齒面方程為：

(8)

式中：τ=θos+θs，rbs為刀具基圓半徑，θs為刀具漸開線上一點的角度參數，μs為刀具漸開線上一點的軸向(沿zs方向)參數，θos確定刀具在基圓上的齒槽寬，并且對標準漸開線刀具用式(9)方程表示：

(9)

式中：Zs為刀具齒數；α0為壓力角.

根據空間坐標變換關系得刀具坐標系osxsyszs到正交變傳動比面齒輪動坐標系s2(x2,y2,z2)的轉換矩陣[15]為：

(10)

式中：γ=ψ+θ1；

A=Dsinβ2sinθ2-Rcosθ2；

B=-Dsinβ2cosθ2-Rsinθ2；

C=r(π)-Dcosβ2．

ψ由公式(17)給出，D,β2在圖4中標出．

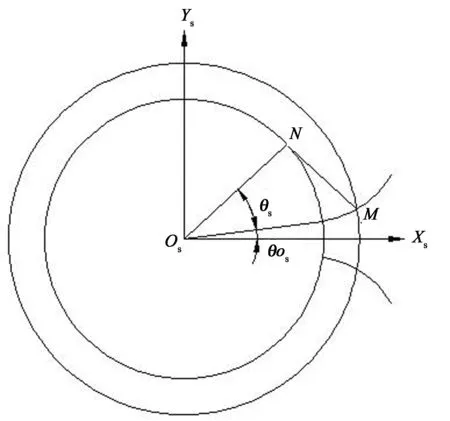
圖2 刀具漸開線齒廓

正交變傳動比面齒輪齒面Σ2是由刀具齒面Σs包絡而成，Σ2可表示為：

(11)

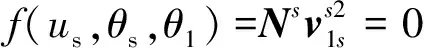
1.4 齒寬設計

1.4.1 正交變傳動比面齒輪不根切的最小內半徑

正交變傳動比面齒輪與一般的定傳動比面齒輪傳動一樣，也存在根切現象.由于根切的存在，正交變傳動比面齒輪的齒寬會受到限制，因此對其根切現象的研究是十分必要的，根據齒輪傳動無根切的通用條件[16]，可以得到加工刀具根切界限線的方程組：

(12)

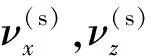
(13)

式中：ras為刀具齒頂圓半徑.

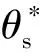
(14)

1.4.2 正交變傳動比面齒輪不變尖的最大外半徑

正交變傳動比面齒輪齒頂變尖的幾何特征是輪齒兩側齒面相交其齒頂厚等于零.圖3是正交變傳動比面齒輪y2o2z2平面的軸截面示意圖，R1和R2分別表示其最小內半徑和最大外半徑.因為y2o2z2平面是正交變傳動比面齒輪輪齒兩側齒廓的對稱平面，所以正交變傳動比面齒輪齒頂變尖處應在y2o2z2平面上，參考圖3，則變尖出的坐標為：

x2=0,y2=-R2,z2=-rsm．

(15)

正交變傳動比面齒輪的齒面方程是關于θs和θ1兩個未知數的方程.由其齒面方程(11)和式(15)的第一和第三式可解出θs和θ1，從而得到正交變傳動比面齒輪不變尖的最大外半徑R2.

求得了正交變傳動比面齒輪不根切的最小內半徑和不變尖的最大外半徑，正交變傳動比面齒輪的齒寬可表示為：

B=R2-R1．

(16)

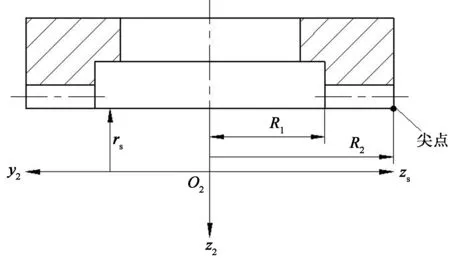
圖3 最大外半徑

2 三維造型

正交變傳動比面齒輪齒面是很復雜的曲面，參考一般定傳動比面齒輪的建模方法，基于現有的三維軟件，主要的建模方法有NURBS自由曲面重構和虛擬加工方法.前者是根據面齒輪齒面方程運用數值方法求解齒面離散點，再在三維軟件中進行曲面重構，實現面齒輪的幾何建模.后者是基于布爾運算原理，模擬刀具和面齒輪毛坯的范成運動，在三維軟件中直接實現面齒輪的幾何建模.由于正交變傳動比面齒輪數值求解過程抽象而繁瑣，因此，本文選用虛擬加工方法在Solidworks軟件中實現正交變傳動比面齒輪的三維造型.

2.1 虛擬加工原理

正交變傳動比面齒輪齒面是通過漸開線齒輪刀具與該面齒輪毛坯做范成運動形成的，運動過程中假想刀具與非圓齒輪內嚙合.由于在Solidworks中無法實現實體的連續運動并且進行相關布爾運算，因此，可以靠每次微小角度的轉動來模擬刀具和正交變傳動比面齒輪毛坯的范成運動.切削該面齒輪的過程，實際上就是正交變傳動比面齒輪毛坯與刀具作布爾減運算的過程.根據相對運動原理，可以假設其毛坯固定，刀具的節曲線在毛坯節曲線上作純滾動，只要確定每一瞬時刀具的空間運動關系，再完成布爾減運算就能得到正交變傳動比面齒輪的三維模型.由于在布爾減運算結果僅余被減物體，因此每次布爾減運算后，都應該對刀具進行復制，實際上每次正交變傳動比面齒輪毛坯與刀具的布爾減運算，減去的是刀具的副本，刀具本身沒有變化.仿真模型的精度是由每次刀具齒輪轉動的步進角控制的，步進角越小，精度越高.

根據嚙合原理和空間幾何關系，加工刀具空間運動關系如圖4所示.φ1，φ2分別為非圓齒輪、正交變傳動比面齒輪轉角，r3為刀具節圓半徑.

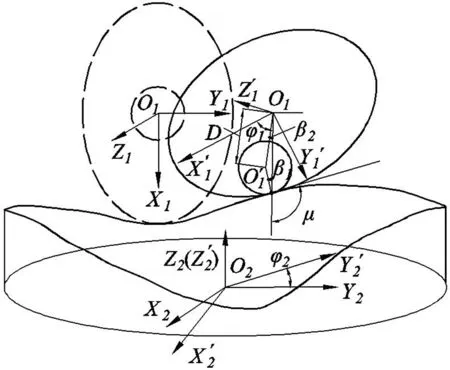
圖4 刀具空間運動關系示意圖

刀具繞自身軸線旋轉角度：

(17)

由微分幾何可得：

(18)

由刀具發生純滾動的弧長與非圓齒輪φ1角對應的弧長相等可得：

(19)

根據余弦定理：

(20)

(21)

x=Dcos (φ1-β2)．

(22)

y=Dsin (φ1-β2)．

(23)

由傳動比關系得，刀具繞面齒輪軸線旋轉角：

(24)

正交變傳動比面齒輪參數化仿真加工模塊的程序流程圖如圖5所示．

2.2 軟件設計

根據以上設計過程及仿真加工原理，基于visual basic語言與Solidworks開發平臺，并結合matlab數學計算軟件，設計出正交變傳動比面齒輪參數化設計及仿真加工軟件，其界面如圖6所示．

參數化設計計算完成后，在仿真加工模塊輸入加工精度，加工起始角度和加工終止角度，依次點擊生成刀具、生成毛坯、仿真加工按鈕，程序會自動調用Solidwork軟件，開始虛擬加工.

2.3 仿真加工實例

分別取n1= [2，3]，n2=[8,12]，k=0.1，z1=[26，27]，m=3，由正交變傳動比面齒輪仿真加工程序得到三維實體后，利用三維軟件自帶的合并曲面功能，將仿真加工時產生的小曲面合并，分別得到的8階和12階正交變傳動比面齒輪模型如圖7所示.

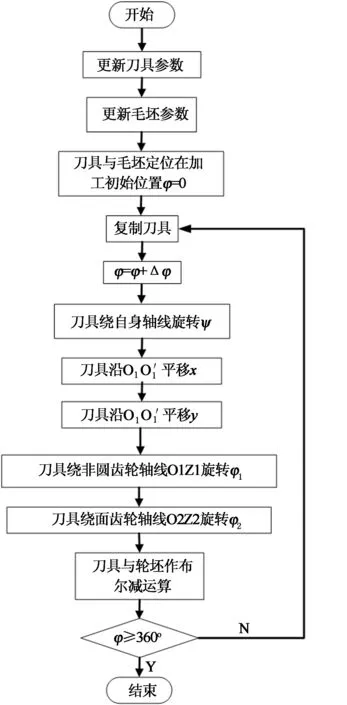
圖5 程序流程圖

圖6 軟件界面

圖7 虛擬加工模型圖

3 實體加工及實驗研究

3.1 實體加工

分別用三軸數控銑削加工和數控電火花線切割加工方法加工出八階正交變傳動比面齒輪和二階非圓齒輪實體.仿真加工模型與實體如圖8所示.由圖8(c)可見，仿真加工模型與實體一致，表明該正交變傳動比面齒輪副的參數化設計及仿真系統的正確性.

圖8 實體加工

3.2 實驗研究

正交變傳動比面齒輪副的試驗臺由變頻直流電動機、轉速扭矩測量儀、正交變傳動比面齒輪副傳動箱、試驗臺架、變速箱綜合測試系統等儀器及設備組成.傳動試驗臺如圖9所示.

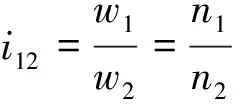
圖9 試驗臺布置

如圖10所示，實驗測定的實際傳動比曲線和理論傳動比曲線在有些部位表現出差異，導致這種差異的原因是齒輪副加工過程存在加工誤差，齒輪的安裝過程存在安裝誤差，同時，傳感器采集數據本身及后期的數據處理過程也有一定的誤差.但是，其變化規律基本相同，變化趨勢基本一致，表明正交變傳動比面齒輪副的設計及三維造型方法是可行的.

4 結 論

1) 建立了正交變傳動比面齒輪嚙合坐標系，由空間坐標轉換原理，得出了各坐標的相互轉換關系，進而推導出了正交變傳動比面齒輪的節曲線、齒頂曲線以及齒根曲線的參數方程.

2) 根據共軛齒廓理論，分析了加工過程中刀具的空間走刀軌跡，推導得到了正交變傳動比面齒輪的齒面參數方程.

3) 由空間齒輪嚙合原理，對正交變傳動比面齒輪的根切和變尖現象進行了詳細的研究，得出了正交變傳動比面齒輪無根切的最小內徑及不產生變尖最大外徑計算方法.

4) 利用Solidworks三維造型功能以及應用程序接口(API)，結合編程軟件VB，開發了正交變傳動比面齒輪的設計與仿真加工系統，得到了正交變傳動比面齒輪的三維實體及其裝配模型，實現了正交變傳動比面齒輪的可視化.

5) 完成了正交變傳動比面齒輪的加工，搭建了正交變傳動比面齒輪副的傳動實驗臺，通過實驗研究，驗證了設計分析方法及加工制造方法的正確性和可行性.

[1] LITVIN F L, ALFONSO F, MATT H． Design generation and TCA of new type of asymmetric face-gear drive with modified geometry[J]. Computer Methods in Applied Mechanics and Engineering, 2001,19(43/44):5837-5865.

[2] 王 志,石照耀,劉建煒,等.正交面齒輪計算機仿真加工[J].北京工業大學學報,2012,38(7):1004-1007.

WANG Zhi,SHI Zhao-yao,LIU Jian-wei,etal. Simulation of orthogonal face gear proceeding[J]. Journal of Beijing University of Technology,2012,38(7):1004-1007. (In Chinese)

[3] 李大慶,鄧效忠,魏冰陽,等.偏置斜齒面齒輪幾何設計及齒寬特性分析[J].機械設計,2011,28(9):59-62.

LI Da-qing, DENG Xiao-zhong, WEI Bing-yang,etal. Tooth geometry design and tooth width characteristics analysis of offset helical face-gear[J]. Journal of Machine Design,2011,28(9):59-62. (In Chinese)

[4] 張會會.非正交面齒輪傳動設計研究[D].濟南:山東大學機電工程學院,2012.

ZHANG Hui-hui.Research on the non-orthogonal face gear drive design[D].Jinan:College of Mechanical and Electrical Engineering, Shandong University,2012. (In Chinese)

[5] MICHELE G, JEAN-PIERRE D V, COLIN-YANN J. Quasi-static analysis of a face gear under torque[J]. Computer Methods in Applied Mechanics and Engineering, 2005,194(39/41): 4301-4318.

[6] FRACKOWIAK P. Modeling and cutting a face-gear with straight line on CNC milling-machine[J]. Manufacturing Engineering, 2010,9 (3):19-21.

[7] FRACKOWIAK P. Forming and geometrical dependences in the nom-homogeneous face-gear with involute line[J]. Manufacturing Engineering ,2010,9 (4): 28-30.

[8] OHSHIMA F , YOSHINO H, NADEHIRO E. A study on high reduction face gears (2nd report, cutting of face gear) [J]. Transactions of the Japan Society of Mechanical Engineers, Part C, 2009,75(758):2816-2821.

[9] WANG Yan-zhong, WU Can-hui,GONG Kang,etal. Loaded tooth contact analysis of orthogonal face-gear drives[J]. Proceedings of the Institution of Mechanical Engineers, 2012,226(9):2309-2319.

[10]ZHAO N, GUO H, FANG Z D,etal. Loaded tooth contact analysis of modified helical face gears[C]// YAN X T, EYNARD B, ION W J，etal. Global Design and Manufacture to Gain a Competitive Edge． London: Springer Verlag, 2008:45-54.

[11]LITVIN F L, ZHANG Y,WANG J C,etal. Design and geometry of face-gear drives[J]. Journal of Mechanical Design,1992,114(4): 642-647.

[12]林超,侯玉杰,龔海,等.高階變性橢圓錐齒輪傳動模式設計與分析[J].機械工程學報,2011,47(13) :131-139.

LIN Chao, HOU Yu-jie, GONG Hai,etal. Design and analysis of transmission mode for high-order deformed elliptic bevel gears[J]. Journal of Mechanical Engineering,2011, 47(13):131-139. (In Chinese)

[13]龔海.正交非圓面齒輪副的傳動設計與特性分析[D].重慶:重慶大學機械工程學院,2012.

GONG Hai. Transmission design and characteristic analysis of orthogonal non-circular face gear drive[D].Chongqing: College of Mechanical Engineering, Chongqing University,2012. (In Chinese)

[14]吳序堂,王貴海.非圓齒輪及非勻速比傳動[M].北京：機械工業出版社,1997:17-19.

WU Xu-tang, WANG Gui-hai. Transmission of noncircular gears and variable ratio[M].Beijing:China Machine Press,1997:17-19. (In Chinese)

[15]楊俊,譚建平,楊武,等.大型水壓機閥芯驅動系統雙圓弧凸輪設計及應用[J].湖南大學學報:自然科學版，2013,40(7):53-58.

YANG Jun , TAN Jian-ping, YANG Wu,etal. Design and application of cam with two arc curvein the spool opening of large water hydraulic press[J]. Journal of Hunan University：Natural Sciences,2013,40(7):53-58.(In Chinese)

[16]李特文 F L.齒輪幾何學與應用理論[M].上海:上海科學技術出版社,2008:112-115.

LITVIN F L. Gear geometry and applied theory[M]. Shanghai: Shanghai Science Press, 2008:112-115. (In Chinese)