廣義直覺模糊軟集的格結構*

周小強, 李慶國

(1. 湖南大學 數學與計量經濟學院, 湖南 長沙 410082; 2.湖南理工學院 數學學院, 湖南 岳陽 414006)

在我們的日常生活中存在許多不確定性問題，現有的處理不確定性問題的工具如模糊集、粗糙集與區間數學等均存在一定的不足，對有些問題不能有效處理.為此，Molodsov提出一種新的處理不確定性問題的數學工具——軟集理論[1].隨后，國內外許多學者從不同角度對軟集進行了深入研究，使軟集理論及其應用得到了迅猛的發展.Maji等將軟集與模糊集相結合，提出了模糊軟集的概念[2].文獻[3-5]將模糊軟集進一步推廣，分別得到直覺模糊軟集、區間值模糊軟集和廣義模糊軟集模型，使軟集的應用更為廣泛.文獻[6-7]從格論的角度分別討論了軟集與模糊軟集的代數性質.本文結合廣義模糊軟集與直覺模糊集，介紹了廣義直覺模糊軟集的概念與相關算子，研究了廣義直覺模糊軟集的代數性質，給出了廣義直覺模糊軟集的兩種具體格結構，并得到了這兩種格都是有界分配格.

1 基本定義

設U是初始論域，E是參數集，P(U)表示U的冪集，序對(U,E)為軟論域，F(U)和IF(U)分別表示U上的所有模糊子集與直覺模糊子集，A,B,C?E，α,β和γ分別表示A,B和C的直覺模糊子集.下面介紹一些基本概念.

定義1[1]設U是初始論域，E是參數集，稱序對(F,A)是軟論域(U,E)上的軟集，其中F:A→P(U)是一個映射.

定義2[8]設U為論域，如果映射μX:U→[0, 1]，νX:U→[0, 1]或記作(μX,νX):U→[0, 1]2，且對h∈U有μX(h)+νX(h)≤1，則稱X={(h,μX(h),νX(h))|h∈U}為U上的一個直覺模糊子集.

定義3[8]設X和Y為論域U的直覺模糊集.直覺模糊集的子集、交、并和補分別定義如下：

1)X?Y?對任意的h∈U有μX(h)≤μY(h)且νX(h)≥νY(h).

2)X∩Y={(h,μX(h)∧μY(h),νX(h)∨νY(h))|h∈U}.

3)X∪Y={(h,μX(h)∨μY(h),νX(h)∧νY(h))|h∈U}.

定義4[3]設U是初始論域，E是參數集，A?E且F:A→IF(U)是一個映射，稱序對(F,A)為軟論域(U,E)上的一個直覺模糊軟集.

定義5[5]設U是初始論域，E是參數集，F:E→F(U)是一個函數，λ是E的模糊子集,也就是μλ:E→[0,1].定義函數Fλ:E→F(U)×[0, 1]，使得對任意的e∈E，Fλ(e)=(F(e),μλ(e))，其中F(e)∈F(U)，μλ(e)∈[0,1].則稱Fλ是軟論域(U,E)上的廣義模糊軟集.

2 廣義直覺模糊軟集及其算子

在本節中，介紹廣義直覺模糊軟集的概念、一些算子及其性質.

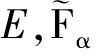
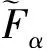
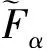
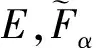
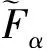
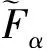
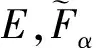
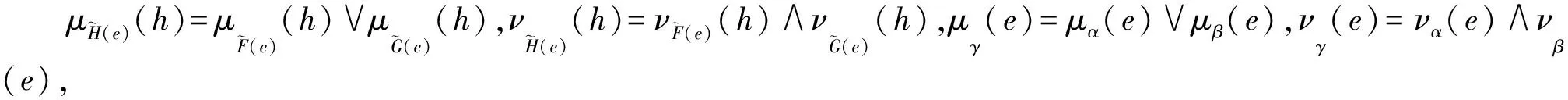
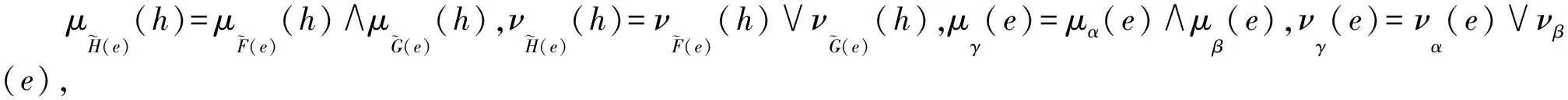
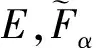
(μγ(e),νγ(e))．

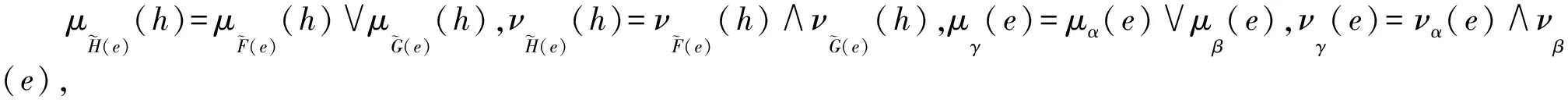
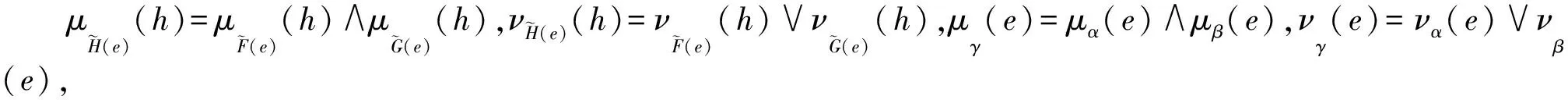
根據以上定義，可以得到以下結論.

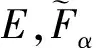
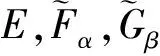
3 廣義直覺模糊軟集的格結構

設GIFS(U,E)表示軟論域(U,E)上的所有廣義直覺模糊軟集的全體, 即GIFS(U,E)=

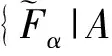
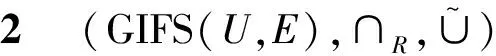
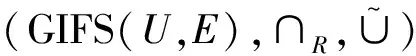
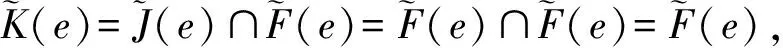
νη(e)=να(e)∨να(e)=να(e).

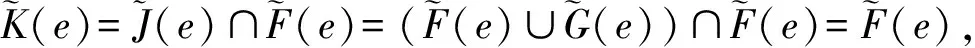
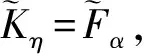
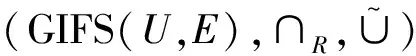
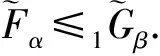
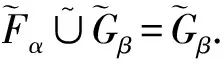
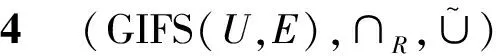
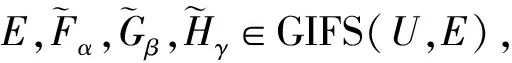
(i) 當e∈B且e∈C時，

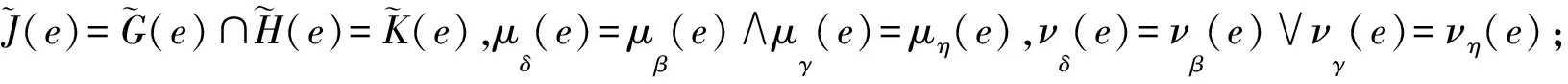
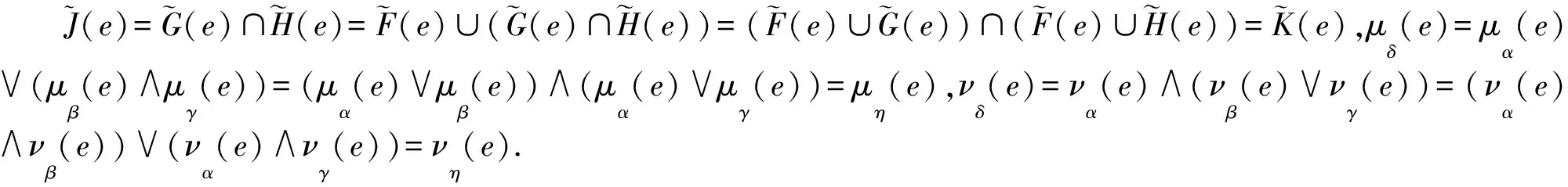
(ii) 當e∈A時，

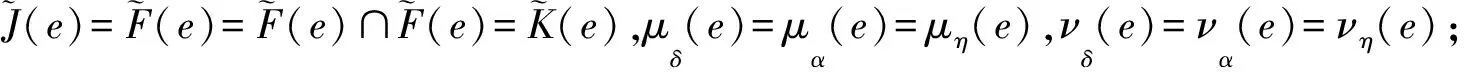
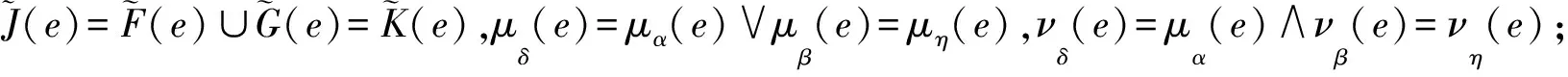
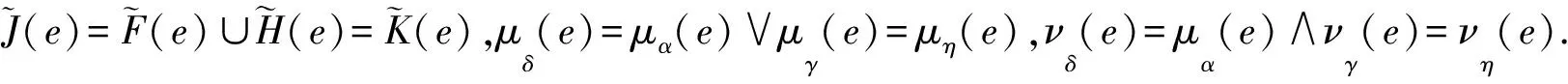
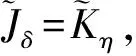
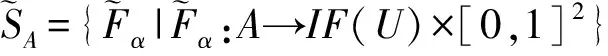
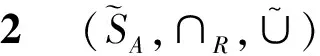
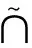
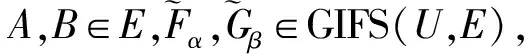
證明與定理2的證明類似(略).

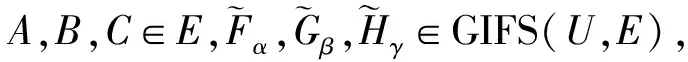
證明與定理4的證明類似(略).

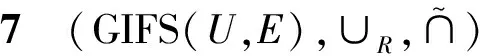
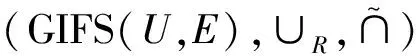
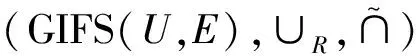
證明與定理3的證明類似(略).

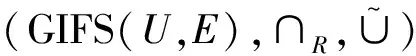
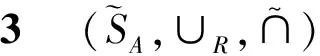
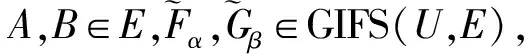
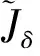
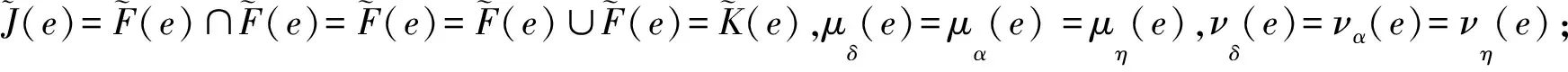
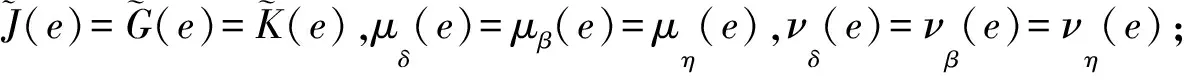
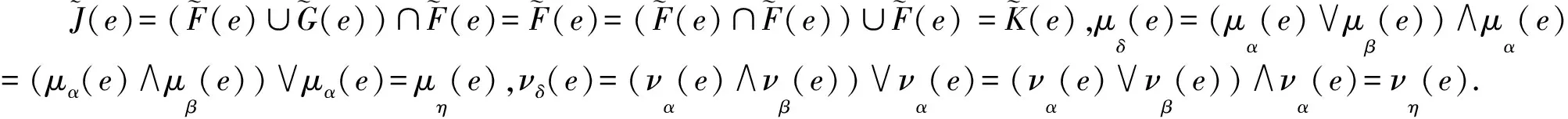
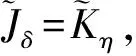
2) 與1)的證明類似.

[1] MOLODTSOV D. Soft set theory-First results [J]. Computers & Mathematics with Applications, 1999, 37: 19-31.

[2] MAJI P K, BISWAS R, ROY A R. Fuzzy soft sets [J]. Journal of Fuzzy Math, 2001, 9:589-602.

[3] MAJI P K, BISWAS R, ROY A R. Intuitionistic fuzzy soft sets [J]. The Journal of Fuzzy Mathematics, 2001, 9: 677-692.

[4] YANG Xi-bei, LIN Young-tsau, YANG Jing-yu,etal. Combination of interval-valued fuzzy set and soft set [J]. Computers & Mathematics with Applications, 2009, 58: 521-527.

[5] MAJUMDAR P, SAMANTA S K. Generalised fuzzy soft sets [J]. Computers & Mathematics with Applications, 2010, 59: 1425-1432.

[6] QIN Ke-yun, HONG Zhi-yong. On soft equality [J]. Journal of Computational and Applied Mathematics, 2010, 234: 1347-1355.

[7] QIN Ke-yun, ZHAO Hua. Lattice structures of fuzzy soft sets [J]. Lecture Notes in Computer Science, 2010, 6215: 126-133.

[8] ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20: 87-96.