平流層飛艇滑模姿態控制系統設計

王領, 郭建國, 周軍, 王國慶

(1.西北工業大學 精確制導與控制研究所, 陜西 西安 710072;2.中國運載火箭技術研究院 研究發展中心, 北京 100076)

0 引言

隨著對臨近空間飛行器研究的不斷深入,平流層飛艇越來越受到世界各國的重視[1-2],其控制技術也成為研究的熱點。針對平流層飛行環境所帶來的特殊問題,以及飛艇自身的飛行控制特性,不少學者開展了平流層飛艇的姿態控制技術研究。文獻[2]針對平流層環境,較為詳細地提出了飛艇的總體結構和動力學建模,并給出了控制方案;文獻[3]針對一種自主飛艇提出動力學建模方法;文獻[4]應用輸入輸出反饋線性化的控制方法設計了飛艇姿態魯棒控制系統;文獻[5]基于神經網絡和變結構控制相結合方法設計了魯棒自適應飛艇控制系統。

針對飛艇在平流層實現定點駐留的任務需求,同時考慮到在平流層飛行的特殊飛行環境中飛艇姿態所產生的通道耦合和不確定性,本文應用反演法[6]來設計動態的滑動模態,以抑制不確定性對姿態的影響,同時也避免了反演法的微分膨脹問題。通過兩個滑動平面的設計,利用Lyapunov穩定理論,設計了一種新的飛艇姿態控制系統,實現了飛艇姿態的穩定控制,并通過數學仿真證明了設計方法的有效性。

1 飛艇姿態控制系統模型

平流層飛艇的姿態動力學模型可借助文獻[2]中給出的非線性姿態動力學模型的建模方法。不失一般性,這里僅考慮俯仰通道姿態動力學模型,該模型不僅考慮到平流層飛行環境對飛艇姿態產生了許多不確定性因素,而且還包含了飛艇的建模誤差和通道耦合。平流層飛艇俯仰通道姿態非線性動力學模型為[3]:

(1)

式中,θ，φ分別為俯仰角和滾轉角;q,r和p分別為繞艇體各軸的角速度分量;Ix,Iy,Iz分別為x,y,z軸向的轉動慣量;Ixz為慣性積；zG,xG為重心在艇體坐標系下的坐標;u,v和w分別為沿艇體各軸的速度分量;M1為除氣動舵面之外產生的其他力矩;aδz為氣動舵面控制力矩,a為飛艇的氣動控制力矩系數。

這里不采用線性化的建模方式,直接針對非線性模型(1),令x1=θ,x2=q,u=δz,則模型(1)可寫為:

(2)

其中：

b=a/Iy，d=x2(cosφ-1)-rsinφ

f(x)= -[(Ix-Iz)pr+Ixz(p2-r2)+

pv-qu)-M1]/Iy

2 非線性姿態控制系統設計

為了使飛艇俯仰通道獲得姿態穩定,這里總體上采用變結構控制方法,在滑動模態上,基于反演法設計自適應的動態滑模,來設計飛艇的姿態控制系統。

設俯仰通道的指令姿態角為θm,則俯仰角跟蹤誤差為:

e=x1-θm

(3)

選擇第一個滑動模態為:

s1=e

(4)

選擇:

(5)

式中,k1>0;ε1>|d|。由此,可得虛擬控制:

x2m=-k1s1-ε1sgn(s1)

(6)

為了避免虛擬變量x2m的直接微分,設計一階動態濾波器:

(7)

式中,τ>0。再選擇第二個滑動模態為:

s2=x2-x2c

(8)

選擇:

(9)

式中,k2>0;ε2大于通道間的未知耦合量的大小。可得姿態控制律:

(10)

由此可得以下定理:

定理1:針對給定的平流層飛艇姿態控制系統(1),如果控制律采取式(10),則在有限時間內飛艇姿態系統中俯仰角達到穩定,并具有一定的魯棒性。

顯然為了說明姿態系統的穩定性,可分別取Lyapunov函數為:

(11)

或

(12)

由式(5)可得飛艇姿態系統中俯仰角在有限時間內收斂到期望角度。只要式(5)成立和式(9)中ε2滿足大于通道間的未知耦合量的大小條件,則飛艇姿態控制系統具有一定的魯棒性。

此外,考慮到變結構控制律(10)含有不連續的符號函數,用飽和函數代替即可,控制律變為:

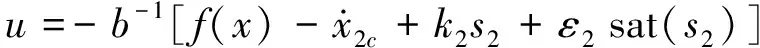
(13)

3 數學仿真及分析

為了說明所設計的飛艇姿態控制系統的有效性,以文獻[2]提供的平流層飛艇數據為例,采用本文設計的滑模姿態控制系統進行數學仿真[7]。考慮飛艇的飛行高度為21 km,環境風速為20 m/s,飛艇初始姿態角均設為1°,同時設定期望的俯仰角為3°。具體仿真參數設定為:k1=0.1,ε1=1,k2=0.1,ε2=1,τ=0.1。

飛艇在俯仰通道上的俯仰角和舵面偏轉角的變化曲線如圖1和圖2所示。從圖1中可以看出,俯仰角在80 s內逐漸收斂并接近3°,由于存在一定的測量誤差,最終俯仰角誤差在0.5°之內;從圖2中可以看出,采用式(13)的變結構控制律,可以有效地削弱原來變結構控制中固有的振蕩問題。

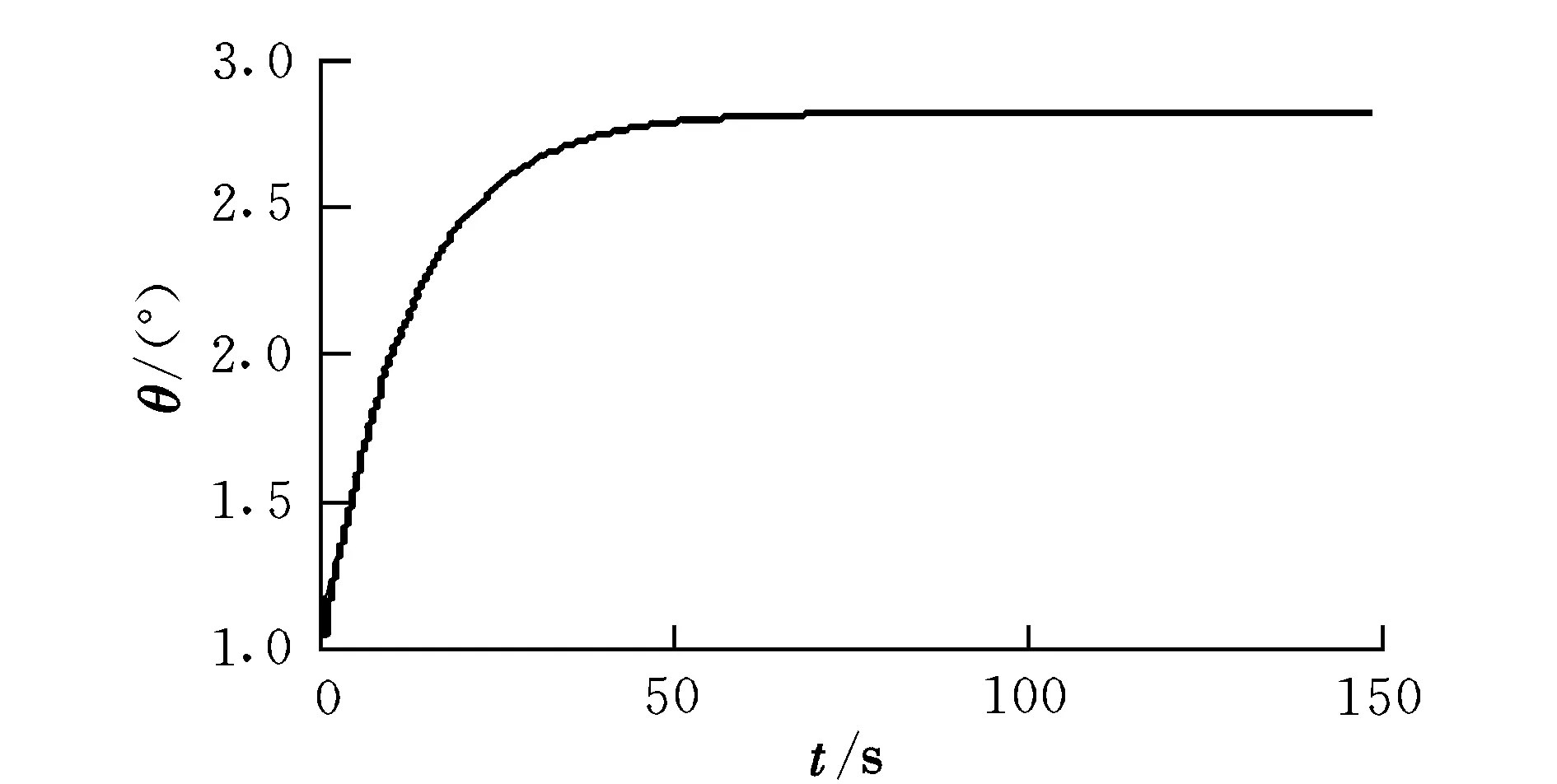
圖1 俯仰角響應曲線Fig.1 Behaviour of pitch angle

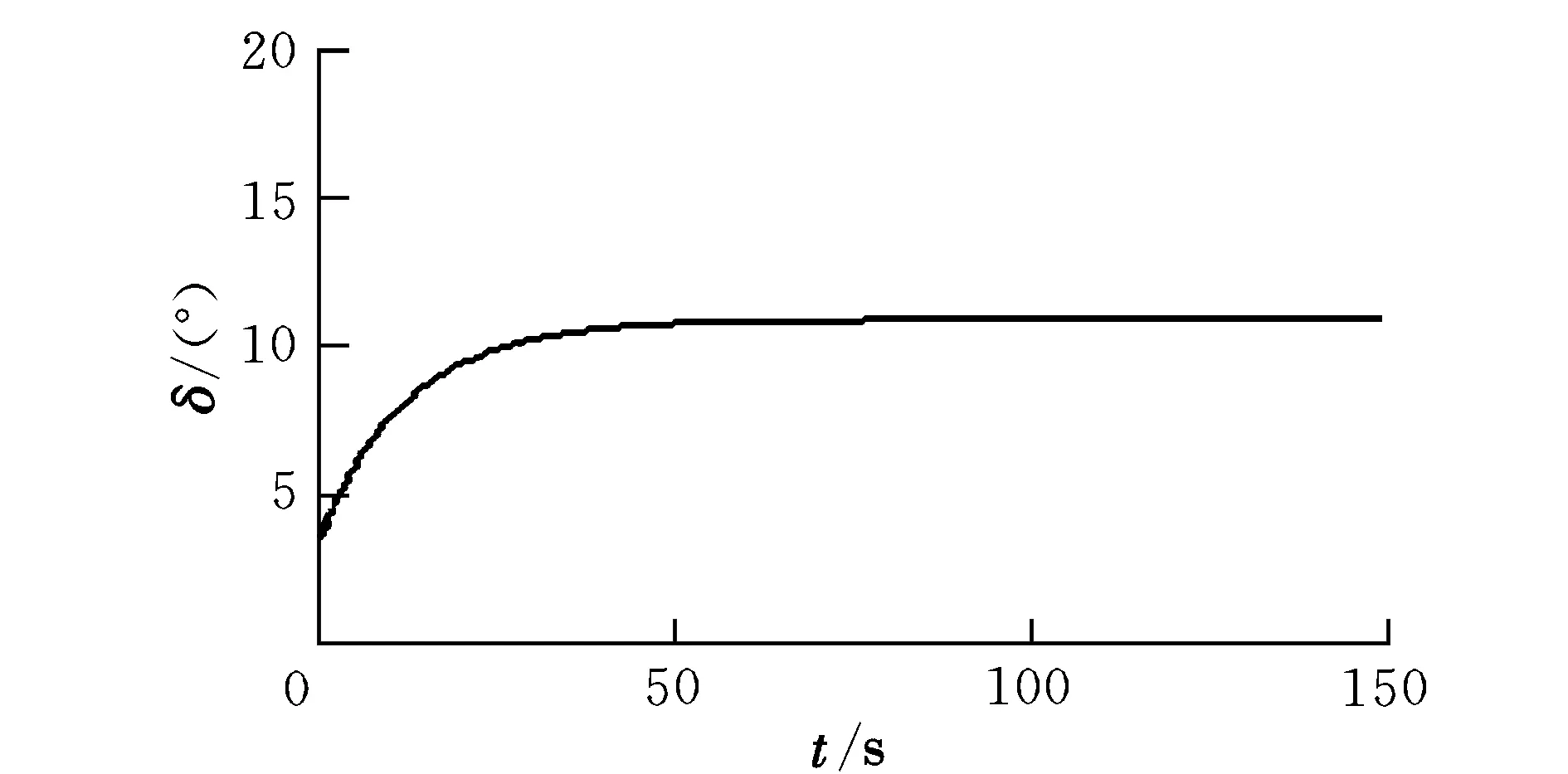
圖2 舵面控制指令Fig.2 Command of control surface

此外,從整個飛艇姿態所獲得的其他通道的仿真結果和俯仰通道的情況相一致,因此,采用反演法和變結構相結合的姿態控制系統,能夠使飛艇適應平流層環境和內部結構參數的影響,并實現良好的跟蹤控制效果。

4 結論

本文針對平流層飛艇設計了魯棒的非線性姿態控制,得到以下結論:采用反演法和變結構設計的動態滑模可以有效地解決飛艇在平流層飛行環境中所存在的不確定性因素,實現姿態的穩定,具有良好的魯棒性。可以將該方法應用于飛艇的定點控制中,便于工程實現。

參考文獻：

[1] Eguchi K,Yokomaku Y,Mori M.Feasibility study program on stratospheric platform airship technology in Japan [R].AIAA-1999-3912,1999.

[2] Joseph B M,Michael A P,Zhao Yiyuan.Development of an aerodynamic model and control law design for a high altitude airship[C]//AIAA 3rd Unmanned Unlimited Technical Conference,Workshop and Exhibit.Chicago,2004:415-431.

[3] Cai Z L,Qu W D,Xi Y G.Dynamic model for airship equipped with ballonets and ballast[J].Applied Mathematics and Mechanics,2009,26(8):1072-1082.

[4] 王曉亮,單雪雄.平流層飛艇姿態魯棒控制研究[J].系統仿真學報,2006,18(5):1271-1274.

[5] 郭建國,周軍.基于滑模神經網絡的自主飛艇姿態控制[J].飛行力學,2009,27(1):40-42.

[6] Zhang T,Zhu Q,Yang Y.Adaptive neural control of non-affine pure-feedback nonlinear systems with input nonlinearity and perturbed uncertainties[J].International Journal of Systems Science,2012,43(4):691-706.

[7] 劉金琨.滑模變結構控制Matlab仿真[M].北京:清華大學出版社,2005:251-255.