自適應視野的人工魚群算法求解最短路徑問題

馬憲民，劉妮

（西安科技大學 電氣與控制工程學院，陜西 西安 710054）

1 引言

最短路徑是智能車輛導航系統(tǒng)中的一個關(guān)鍵問題，在求解最短路徑的算法中，目前國內(nèi)外公認的較好算法有經(jīng)典的迪杰斯特拉(Dijkstra)及弗洛伊德(Floyd)算法，但時間復雜度是此2種算法的瓶頸[1~3]。隨著人工智能研究的深入，一些新的智能優(yōu)化算法不斷被提出，包括遺傳算法、蟻群算法、粒子群算法、人工魚群算法等。遺傳算法的主要缺點是對于結(jié)構(gòu)復雜的組合優(yōu)化問題，搜索空間大，搜索時間比較長，往往會出現(xiàn)早熟收斂的情況；對初始種群很敏感，初始種群的選擇常常直接影響解的質(zhì)量和算法效率[4]。基本蟻群算法搜索時間長，而且容易出現(xiàn)停滯，存在著收斂速度慢、易陷入局部最優(yōu)等缺陷；而模型中各參數(shù)的取值更直接關(guān)系到算法的收斂速度和全局搜索能力[4,5]。粒子群算法雖然收斂速度較快，但精度較低、易發(fā)散，容易陷入局部最優(yōu)解[4]。而人工魚群算法（AFSA，artificialfish swarm algorithm）頑健性強、對初值的敏感性小、簡單（只需比較目標函數(shù)）、易實現(xiàn)，而且具有較強的跳出局部極值點的能力，即全局收斂性好，這就能為最短路徑問題搜索到準確的全局最優(yōu)解。

例如，文獻[6]將改進的人工魚群算法應用于交通路徑誘導系統(tǒng)數(shù)據(jù)庫優(yōu)化查詢中，算法提高了最優(yōu)路徑查詢的效率。文獻[7]基于有限適合啟發(fā)式算法與人工魚群算法相結(jié)合，完成了車輛最優(yōu)調(diào)度路徑的準確迭代計算，縮短了計算時間，克服了傳統(tǒng)方法收斂速度慢的缺陷，高效地完成了最優(yōu)路徑的準確選擇。

因此，本文選擇人工魚群算法求解靜態(tài)道路網(wǎng)絡(luò)上指定起點到終點的最短路徑，并且針對基本人工魚群算法在后期收斂速度慢和計算量大的缺陷，提出了基于視野自適應的改進算法。該改進算法只對人工魚的覓食行為的視野進行改變，使其隨著迭代次數(shù)的增加而逐漸減小，從而有效地加快了算法的收斂速度，減小了計算量。

2 基本人工魚群算法

人工魚群算法是我國學者李曉磊等人在 2002年模仿魚類行為特點提出的一種基于動物自治體的優(yōu)化策略[8]。該算法的基本思想是[9]：在一片水域中，魚類聚集最多的地方一般就是這片水域中食物最為豐富的地方；根據(jù)魚類的這個特點構(gòu)造人工魚，模仿魚群的覓食、聚群、追尾等行為，每條人工魚對應一個優(yōu)化解，人工魚生存的虛擬水域?qū)趦?yōu)化問題的解空間，食物濃度對應于目標函數(shù)值，通過人工魚群在虛擬水域中游動實現(xiàn)尋優(yōu)。人工魚群行為的算法描述如下。

1) 覓食行為：設(shè)人工魚的當前狀態(tài)為aX，在其視野范圍內(nèi)隨機選擇一個狀態(tài)bX ，為

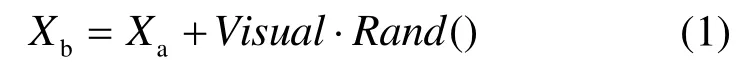
其中，函數(shù) ()Rand 產(chǎn)生0到1之間的隨機數(shù)，Visual為視野范圍。如果食物濃度(求極小值問題)則向該方向前進一步，為

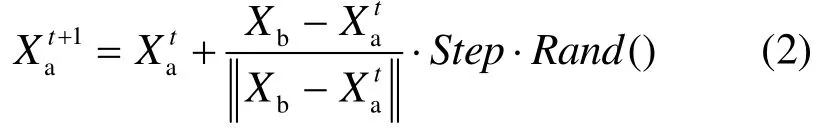
其中，Step為移動步長。反之，再重新隨機選擇狀態(tài)bX，判斷是否滿足前進條件；試探一定次數(shù)后，如果仍不滿足前進條件，則執(zhí)行其他行為，如隨機移動行為

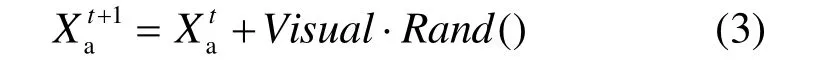
2) 聚群行為：設(shè)人工魚的當前狀態(tài)為aX，探測其鄰域的伙伴數(shù)目nf，如果表明伙伴中心有較多的食物且不太擁擠，并且Ya＞Yc，則向中心位置Xc前進一步，為

否則，執(zhí)行其他行為（如覓食行為）。

3) 追尾行為：設(shè)人工魚當前狀態(tài)為 Xi，探測其鄰域內(nèi)狀態(tài)最優(yōu)的鄰居 Xmax，如果，并且Xmax的鄰域內(nèi)伙伴數(shù)目nf滿足＜ 1 )，表明 Xmax附近有較多的食物且不太擁擠，則向 Xmax的方向前進一步，為

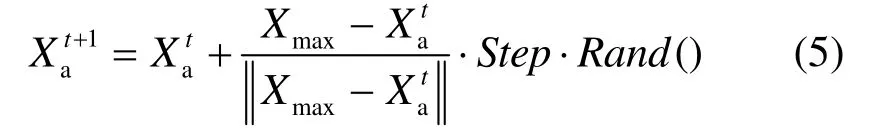
否則執(zhí)行覓食行為。

4) 隨機行為：人工魚在視野范圍內(nèi)隨機選擇一個狀態(tài)，然后向該方向移動，其實是覓食行為的一個默認缺省行為

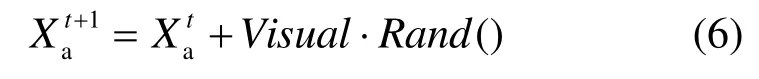
5) 公告板：主要用于記錄優(yōu)化過程中最優(yōu)人工魚個體的狀態(tài)。

3 改進人工魚群算法求解最短路徑問題的原理

3.1 基本人工魚群算法求解最短路徑問題的缺陷

從人工魚的基本行為算法描述中可以看出，視野在尋優(yōu)過程中是非常重要的。在反復的實驗過程中發(fā)現(xiàn)，參數(shù)視野固定不變，導致算法后期收斂速度慢，且算法的計算量較大；當路網(wǎng)的節(jié)點數(shù)目較大時，甚至陷入局部最優(yōu)，無法搜索到全局最優(yōu)解。

因為在參數(shù)視野不變的情況下，當人工魚逐漸逼近最優(yōu)解時，只有很少的人工魚狀態(tài)不同于最優(yōu)解的人工魚狀態(tài)，所以，人工魚在最優(yōu)解附近以原始的視野進行覓食是盲目的。在這種情況下，當給定的視野很大，算法的前期收斂很快，但后期收斂很慢，且Trynumber的試探次數(shù)會很大，增加算法的計算復雜性；如果給定的視野很小，則會使收斂變慢，計算量大，甚至陷入局部最優(yōu)。這將降低最短路徑搜索效率和準確性。

3.2 解決的辦法

為了解決上述問題，提出視野自適應的人工魚群算法（AVAFSA，artificial fish-swarm algorithm based on adaptive vision)。

由于人工魚的覓食行為是算法收斂的基礎(chǔ)，所以聚群行為和追尾行為的視野保持不變，只對覓食行為的視野改進，采用自適應的視野，在算法的初始階段，給覓食行為一個較大的視野，隨著算法的迭代進行，逐漸減小視野。

但是，經(jīng)測試發(fā)現(xiàn)，當算法后期的視野太小，算法搜索到全局最優(yōu)解的概率會變小。所以，在該視野自適應的改進人工魚群算法中，當視野的當前值小于初始值的一半時，停止減小，使其保持為初始值的一半（當然也可以根據(jù)具體問題設(shè)置參數(shù)視野值的下限）。算法的表達式為

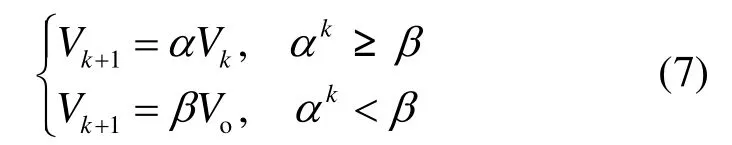
3.3 自適應視野人工魚群算法最短路徑實現(xiàn)原理

人工魚群算法是求解 TSP問題的一個有效方法，而TSP問題與指定起點到目標點的靜態(tài)最短路徑問題的相同點是：兩者都屬于組合優(yōu)化問題。區(qū)別在于：TSP的每一種路徑都要遍歷所有的城市，而指定 2點間的最短路徑問題不需要遍歷每個節(jié)點。所以，本文在人工魚群算法求解最短路徑問題中，借鑒了文獻[10]中人工魚群算法求解TSP的編碼方式，但算法模型有2點不同。

1) 目標函數(shù)：從起點到目標點所經(jīng)過的路徑段的道路權(quán)重(經(jīng)濟、時間、距離的加權(quán)組合)求和。若某條人工魚所代表的路徑（以6個網(wǎng)絡(luò)節(jié)點為例）為：N4、N1、N2、N3、N6、N5，要求的路徑為起始節(jié)點1到終點節(jié)點6的最短路徑，則該人工魚的目標函數(shù)

2) 新路徑的產(chǎn)生

（a）交換節(jié)點與節(jié)點在路徑序列中的位置，將得到新的路徑；

（b）從起點到目標點所經(jīng)過的節(jié)點數(shù)目不同，也將產(chǎn)生新的路徑。

3.4 改進人工魚群算法求解最短路徑問題的步驟

算法的實現(xiàn)步驟如下。

1) 輸入原始數(shù)據(jù)，獲取路網(wǎng)節(jié)點數(shù) P o i ntNum、各節(jié)點的具體坐標位置 P o i ntP osition[]、節(jié)點的權(quán)值矩陣 e dge[]、獲取人工魚群的群體規(guī)模FishNum、最大迭代次數(shù) I terate_times、人工魚的視野初始值Visual、最多試探次數(shù)Trynumber、人工魚的最大移動步長Step、擁擠度因子δ等參數(shù)。

2) 當前迭代次數(shù) P assed _ t imes= 0 ，生成FishNum個人工魚個體，形成初始魚群，每一個人工魚代表從起點到目標點的一種路徑，即從起點至終點的隨機序列。

3) 各人工魚分別模擬執(zhí)行覓食行為、追尾行為和聚群行為；選擇最優(yōu)行為執(zhí)行，缺省行為方式為覓食行為。

4) 各人工魚每行動一次后，檢驗自身狀態(tài)與公告牌狀態(tài)，若自身狀態(tài)優(yōu)于公告牌狀態(tài)，則以自身狀態(tài)取代公告牌狀態(tài)。

5) 終止條件判斷。判斷 p assed _ times是否已達到預置的最大迭代次數(shù) I terate_times，若是，則輸出計算結(jié)果（公告牌的值）；否則， P assed _ times=Passed _ t imes+ 1，轉(zhuǎn)步驟3)。

4 算法的仿真

4.1 道路網(wǎng)拓撲結(jié)構(gòu)

某道路網(wǎng)的無向賦權(quán)拓撲如圖1所示，路網(wǎng)中共有9個節(jié)點。用 wi,j(t)表示每一路段的非負權(quán)值，靜態(tài)環(huán)境下，常數(shù)，表示從節(jié)點 vi出發(fā)到達節(jié)點 vj所需要的行駛代價（時間或費用），若路段(vi, vj)不連通，則其權(quán)重，同一個節(jié)點的權(quán)重為

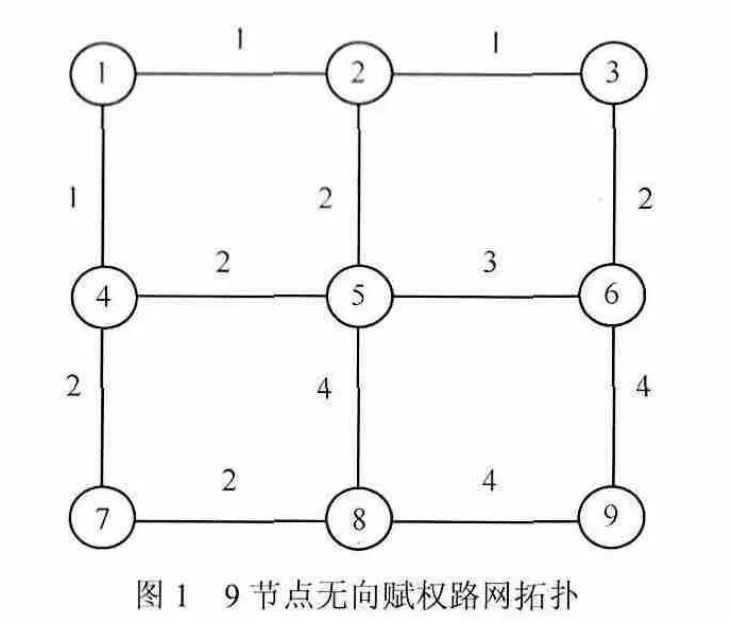
圖1 9節(jié)點無向賦權(quán)路網(wǎng)拓撲

則路網(wǎng)中的權(quán)重可用矩陣表示為

4.2 仿真結(jié)果與數(shù)據(jù)分析

9節(jié)點路網(wǎng)拓撲圖如圖1所示，假設(shè)起點為節(jié)點1，終點為節(jié)點9，權(quán)重矩陣如式（8）所示，則利用人工魚群算法計算這2點間的靜態(tài)最短路徑。

現(xiàn)在將對上述改進型的自適應視野人工魚群算法求解最短路徑方法進行仿真，并與基本人工魚群算法及蟻群算法優(yōu)化結(jié)果進行對比。仿真環(huán)境為：Pentium（R）Dual-Core，2.19 GHz，2.00 G內(nèi)存的計算機。仿真工具為： Matlab R2010a。參數(shù)路阻∞=100，人工魚群算法參數(shù)：人工魚數(shù)目FishNum= 1 0，最大迭代次數(shù) I terate_ t imes= 2 00，最大試探次數(shù) T rynumber= 1 00，初始化視野 V isual=5（根據(jù)節(jié)點數(shù)給定），擁擠度因子deta = 0 .8。蟻群算法參數(shù)：最大迭代次數(shù) N cMax= 2 00，蟻群規(guī)模m=10，留在每個節(jié)點上的信息量受重視程度α=0.1，啟發(fā)式信息受重視程度β=2，信息的保留率ρ=0.1。

因為蟻群算法、基本人工魚群算法和自適應視野的改進人工魚群算法最終都以 100%的成功率搜索到了全局最優(yōu)解，所以圖2給出改進算法求得的最短路徑。所求的最優(yōu)解為 8，得出的路徑為1→2→3→6→9→8→4→7→5；其中 1→2→3→6→9為所求的從起點1至目標點9的最短路徑。

圖3為9節(jié)點路網(wǎng)中基本蟻群算法、基本人工魚群算法及自適應視野的改進人工魚群算法的尋優(yōu)過程對比。3種算法分別在第2次、5次、3次迭代后搜索到全局最優(yōu)解。可以看出改進魚群算法比基本魚群算法的收斂速度快。蟻群算法雖然以最快速度搜索到最優(yōu)解，但搜索過程中出現(xiàn)“之”字形路徑，不穩(wěn)定。

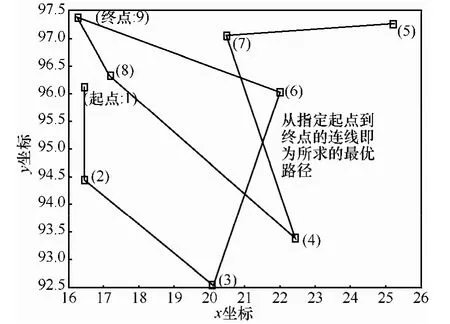
圖2 視野自適應人工魚群算法（AVAFSA）搜索的最短路徑

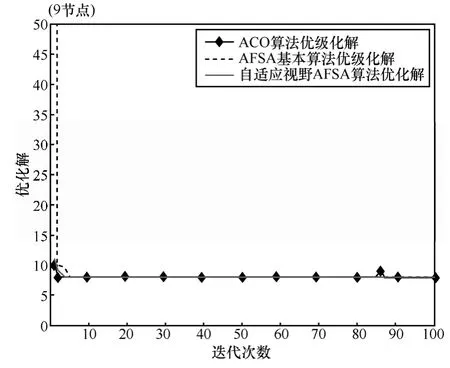
圖3 ACO、基本AFSA與改進的AVAFSA收斂曲線

下面重點對3種算法的計算量和收斂速率進行比較，仿真環(huán)境和初始條件不變，對比實驗結(jié)果如表1所示。

表1對3種算法各取5次仿真實驗數(shù)據(jù)，其中，BEST_GEN表示算法首次搜索到最優(yōu)解的迭代次數(shù)，BEST表示最優(yōu)解（即最短路徑總長度），TIME表示算法迭代200次花費的時間。分析表1的實驗數(shù)據(jù)，可以明顯地看出，基本蟻群算法在求解簡單路網(wǎng)的最短路徑時，速度還是很快的。改進人工魚群算法比基本人工魚群算法的運算量小，收斂性好。也驗證了自適應視野改進算法的可行性和高效性。

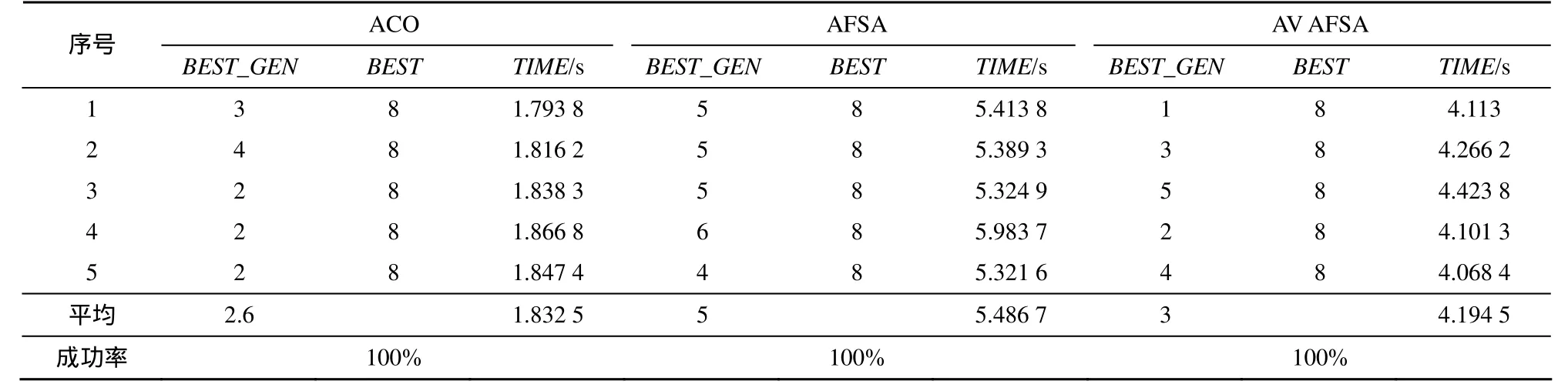
表1 9節(jié)點ACO、AFSA及AVAFSA算法的對比實驗結(jié)果

為了驗證算法的高效、穩(wěn)定性，假設(shè)路網(wǎng)更復雜些，抽象為 16節(jié)點的賦權(quán)無向圖，其道路權(quán)重的鄰接矩陣為

圖4為改進的自適應視野人工魚群算法得出的16節(jié)點靜態(tài)最優(yōu)路徑為7→4→3→2→12→14→1→5→9→10→11→15→16→6→13→8，其中，1→5→9→10→11→15→16為所求的從起點1到終點16的最短路徑。最優(yōu)值為19。

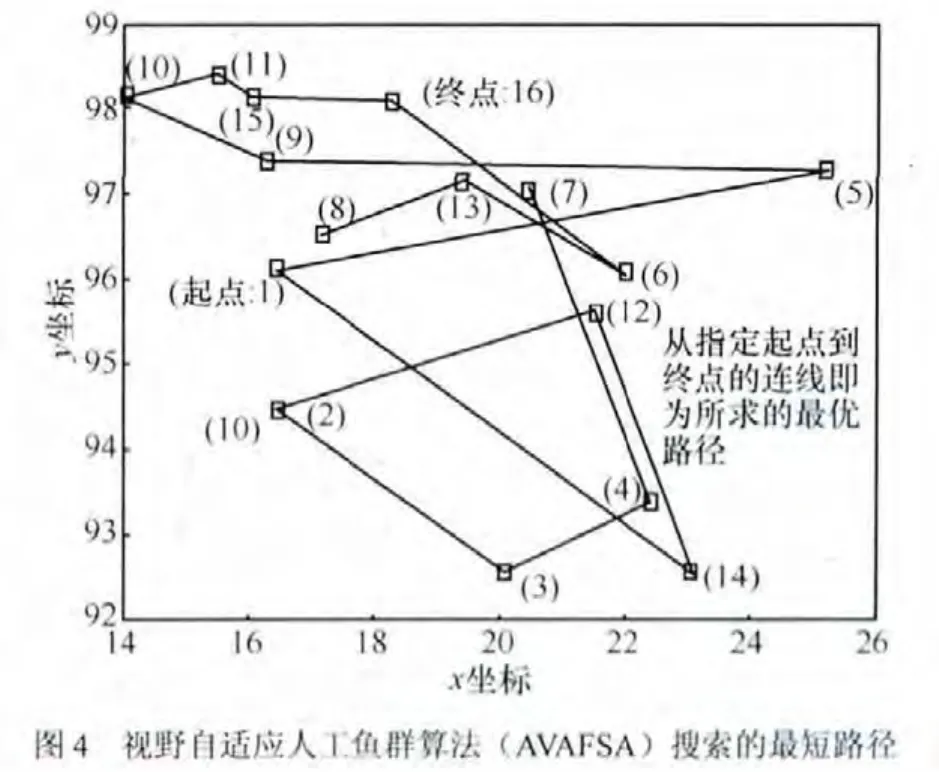
圖4 視野自適應人工魚群算法（AVAFSA）搜索的最短路徑

圖5 為16節(jié)點路網(wǎng)中，基本蟻群算法、基本人工魚群算法及自適應視野的改進人工魚群算法的尋優(yōu)過程對比。可以看出蟻群算法由于沒有方向性引導，在路網(wǎng)變復雜時，搜索過程中的“之”字形路徑現(xiàn)象更嚴重；又因為其概率性和正反饋作用，使算法陷入了局部最優(yōu)，最終不能得到全局最優(yōu)解。基本人工魚群算法在迭代93次后得到全局最優(yōu)解，而改進人工魚群算法在迭代35次后就得到全局最優(yōu)解。顯然，改進的自適應視野的人工魚群算法比基本魚群算法的后期收斂速度快，而且，路網(wǎng)越復雜（節(jié)點越多），該改進算法的優(yōu)勢越明顯。

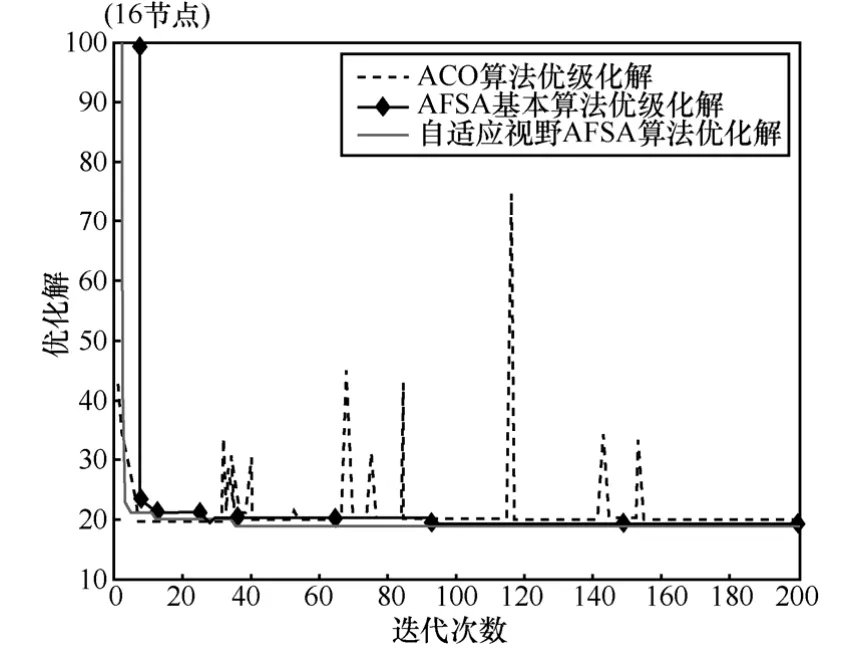
圖5 ACO、基本AFSA及AVAFSA收斂曲線

下面對ACO、AFSA和AVAFSA的計算量和收斂速率進行比較，仿真環(huán)境和初始條件與上面的 9節(jié)點完全相同，對比實驗結(jié)果如表2所示。

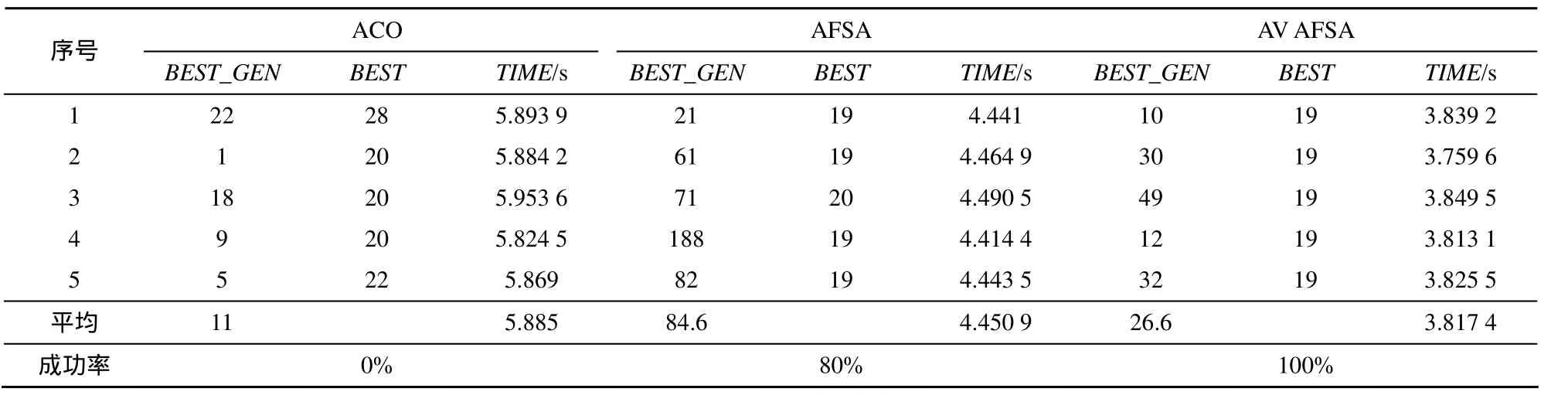
表2 16節(jié)點ACO、AFSA及AVAFSA算法的對比實驗結(jié)果

從表2可以明顯地看出，基本蟻群算法在路網(wǎng)復雜時，搜索不到全局最優(yōu)解，只能得出較優(yōu)解，而且算法時間復雜度明顯增加。而本文視野自適應的改進人工魚群算法比基本人工魚群算法收斂速度快、運算量小，而且準確性高。與表 1對比，得出路網(wǎng)越復雜，該改進算法的優(yōu)越性越突出，說明該改進算法是一種高效、穩(wěn)定的最短路徑求解方法。

5 結(jié)束語

針對基本人工魚群算法因參數(shù)視野固定不變而導致算法后期收斂速度慢、運算量大、陷入局部最優(yōu)的缺陷，本文根據(jù)車輛導航系統(tǒng)中的靜態(tài)最短路徑問題的特點，對人工魚群算法進行了改進。該改進算法只對人工魚的覓食行為的視野進行調(diào)整，使其隨著迭代次數(shù)的變化而自適應地變化，并設(shè)置了視野值的下限，以防視野過小，算法又陷入局部最小。實驗結(jié)果表明，改進型人工魚群算法的收斂速度、計算量、尋優(yōu)精度和準確性均優(yōu)于基本蟻群算法及基本人工魚群算法，而且道路越復雜，節(jié)點越多，這種優(yōu)勢越顯著。

[1] 孫中華. GIS路徑尋優(yōu)中的蟻群算法研究[D]. 南京: 南京理工大學,2009.SUN Z H. Research on Ant Colony Algorithm in GIS Path Optimization[D]. Nanjing: Nanjing University of Science and Technology, 2009.

[2] 譚國真, 高文. 時間依賴網(wǎng)絡(luò)最小時間路徑算法[J]. 計算機學報,2002, 25(2):165-172.TAN G Z, GAO W. The minimum time path algorithm of the time-dependent network[J]. Chinese Journal of Computers, 2002,25(2):165-172.

[3] 王海梅. 基于 GIS的最優(yōu)路徑算法研究與實現(xiàn)[D]. 南京: 南京理工大學, 2008.WANG H M. Research and Implementation of the Optimal Path Algorithm Based on the GIS[D]. Nanjing: Nanjing University of Science and Technology, 2008.and Technology, 2008.

[4] 甘榮偉. 蟻群優(yōu)化算法及其應用研究[D]. 廣州: 中山大學, 2009.GAN R W. Research on Ant Colony Optimization and Its Application[D]. Guangzhou: Sun Yat-sen University, 2009.

[5] 張學敏, 張航. 基于改進蟻群算法的最短路徑問題研究[J]. 自動化技術(shù)與應用, 2009, 28(6):4-7.ZHANG X M, ZHANG H. Research on the shortest path problem based on an improved ant colony algorithm[J]. Automation Technology and Application, 2009, 28(6):4-7.

[6] 潘海珠, 杜曉昕, 王波. 基于人工魚群的交通誘導系統(tǒng)最優(yōu)查詢研究[J]. 齊齊哈爾大學學報, 2012,28(5):6-9.PAN H Z, DU X X, WANG B. Research on the optimal query research of traffic guidance system based on artificial fish-swarm algorithm[J].Journal of Qiqihar University, 2012, 28(5):6-9.

[7] 鄭根讓. 基于混合人工魚群算法車輛擁堵調(diào)度方案[J]. 計算機仿真, 2012, 29(6):328-331.ZHEN G R. Vehicle congestion scheduling scheme based on a mixed artificial fish-swarm algorithm[J]. Computer Simulation, 2012, 29(6):328-331.

[8] 李曉磊, 邵之江, 錢積新. 一種基于動物自治體的尋優(yōu)模式：魚群算法[J]. 系統(tǒng)工程理論與實踐, 2002, 22(11):32-38.LI X L, SHAO Z J, QIAN J X. An optimization mode based on Autonomous: fish-swarm algorithm[J]. Systems Engineering Theory and Practice, 2002, 22(11):32-38.

[9] 李曉磊. 一種新型的智能優(yōu)化方法—人工魚群算法[D]. 杭州: 浙江大學, 2003.LI X L. A New Type of Intelligent Optimization Method: Artificial Fish-swarm Algorithm[D]. Hangzhou: Zhejiang University, 2003.

[10] 江銘炎, 袁東風. 人工魚群算法及其應用[M]. 北京: 科學出版社,2012.JIANG M Y, YUAN D F. Artificial Fish-swarm Algorithm and Its Application[M]. Beijing: Science Press, 2012.