一種基于C均值的模糊核聚類圖像分割算法

彭建喜

(佛山職業技術學院，廣東佛山 528000)

圖像分割是把圖像分解成具有特殊含義的不相交的空間區域，然后分離出有價值目標的技術和過程，是成功進行圖像分析、模式識別與理解和圖像編碼的關鍵技術之一，圖像分割的質量直接到影響后面進行的分析、識別和解釋的質量［1-2］。近年來，隨著人們對圖像分割進行深入的研究，提出了各種圖像分割方法，包括直方圖閾值的方法、最大熵值方法、區域分割增長的方法和微粒群優化的分割方法等，其中Bezdek提出的模糊聚類算法FCM，是一種基于目標函數的非線性迭代最優化方法，通過引入像素聚類樣本到聚類中心的隸屬度來表示像素樣本的隸屬度，該類隸屬度的大小能夠客觀反映出算法中樣本點隸屬于某一類的程度［3］。但FCM算法對初值敏感，很大程度上依賴初始聚類中心的選擇，并且容易收斂于局部極小值，用于圖像分割時，隸屬度的計算只考慮了圖像中當前的像素探值，而未考慮鄰域像素點的空間信息，故對分割含有噪聲圖像不理想。為了有效解決FCM圖像分割方法所存在的問題，Yang和Chuang等人從不同角度考慮了像素點的空間信息，Gomez提出了一種自適應的空間聚類算法，該算法提出在模糊C均值聚類算法的目標函數中加入像素點空間信息，提高算法的魯棒性，但對于對低灰度信息的圖像分割，該算法就會失效。劉剛等采用輪廓波變換在變換域對圖像做降噪預處理，但容易在處理結果中產生偽吉布斯效應，Chuang為解決低灰度信息問題，通過在目標函數中加入徑向基函數來區分像素點之間的相似度［4-10］。針對以前方法的進行研究與分析，本文對FCM分割算法的改進主要在兩個方面:首先，建立一種新的稱為近似模糊C均值聚類算法，通過數據約簡大幅度降低數據個數，節省計算時間;然后在FCM算法中利用核函數將約簡后的數據映射到非線性高維空間中進行聚類劃分，最后使用像素點的空間鄰域信息修正當前像素空間的隸屬度值，得到更加準確的聚類結果。

1 經典的模糊C均值聚類分割算法

由Bezdek提出的模糊C均值聚類算法，其實質是根據圖像分解后像素樣本與每個聚類中心的加權相似性測度，通過對目標函數進行非線性迭代優化方法，然后確定最優聚類，它給出每個樣本隸屬于某個聚類的隸屬度，即使對于很難明顯分類的變量，FCM也能得到較為滿意的效果。FCM通過將圖像I={f(x，y)，0≤x＜m，0≤y＜n}分成C類來實現圖像的分割，其中f(x，y)為特征數據，Qk(x，y)是f(x，y)對于第k類的隸屬度，為了計算各個樣本點相對于聚類中心的隸屬度，聚類目標函數可定義為

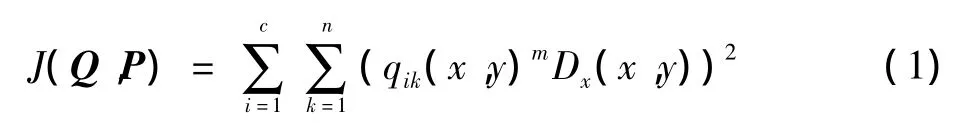
式中:Q=［qik(x，u)］為模糊分類矩陣;P=［p1，p2，…，pc］為聚類中心集合;m∈［1，∞)是控制聚類結果的權指數，一般賦值為2;Dx(x，y)為f(x，y)到聚類中心pk的距離，表示為

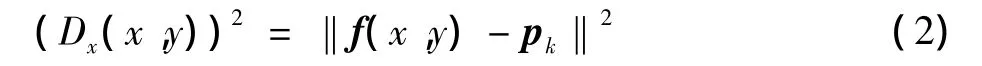
圖像FCM分割就是通過多次迭代確定隸屬度函數和聚類中心，使目標函數獲得最小值。利用拉格朗日乘數法來求解使得J(Q，P)達到最小值的滿足下列等式

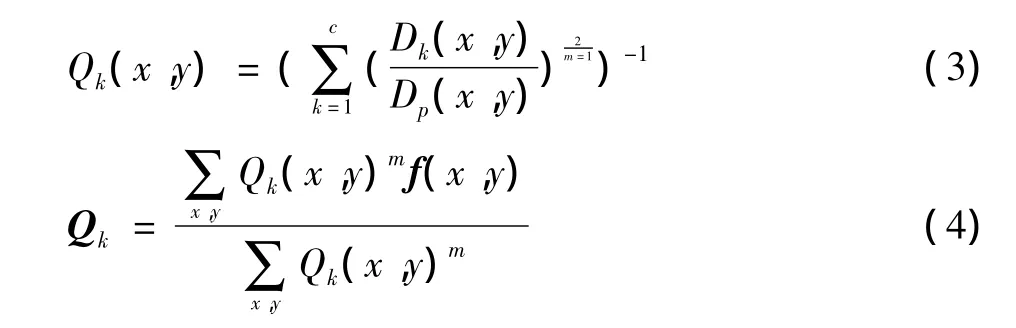
Bezdek利用梯度下降方法，通過對模糊分類矩陣Q與聚類中心矩陣V不斷進行迭代算法，以修正聚類中心值以及各樣本的隸屬度，最終尋找出樣本數據所含有的分類特性，使各樣本劃分到其隸屬度最大的一類中。該算法對初始聚類中心或隸屬度矩陣有較為敏感，參數初值選取決定著聚類結果的優劣和穩定性;當初始聚類中心偏離全局最佳聚類中心比較大時，FCM很有可能陷入局部最小值。

2 近似模糊C均值聚類的中心初始化

2.1 數據約簡

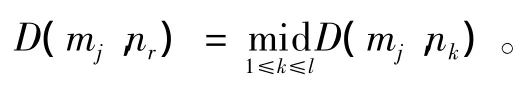
3)如果D(mj，nr)＞γ，l=l+1，nl=mj;否則，令nr=nr∪mj，j=j+1 。

4)如果j＜i，則轉到步驟2);否則，將nk更新為其自身數據集合的平均值。

2.2 加入特征空間中的模糊核聚類算法

在線性空間中難以劃分的問題利用核映射處理來處理，將數據從線性空間映射到高維的非線性空間解決。

先通過一個非線性映射Φ:X→F(X∈Rp→Φ(x)∈Rq，q＞p)將輸入空間X變換至高維特征空間F;然后在特征空間F中進行聚類。

對在FCM目標函數中使用核映射，則得到目標函數息，得到與模糊C均值接近的聚類中心。

設原始數據集合M中含有i個不同的樣本M={m1，m2，…，mn}?Rs。分析聚類問題就是將 {m1，m2，…，mi}區分為M中的c(2≤c＜i)個子集，相似的樣本應要求盡量在同一子集(聚類)內，c為聚類數目。約簡后數據集合為N={n1，n2，…，ni}?Rs。D(m，S)表示數據m與數據集合S間的距離。則數據約簡算法的步驟如下:

1)初始化閾值，其中 γ，l=1，nl=m1，j=2 。

2)對聚類樣本數據mj，計算整數值r，使其滿足

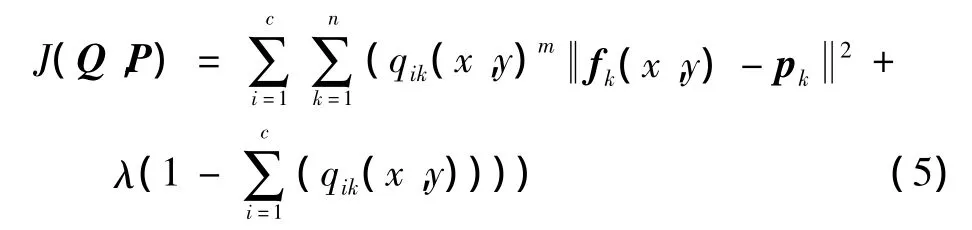
其中

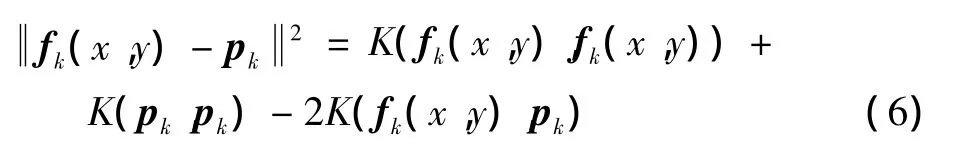
由核代入技巧知，上述內積定義了F中的一個核函數K(x，y)，滿足K(x，y)=(fk(x，y)－pk)T(fk(x，y)－pk)。Dx(x，y)為特征空間中的歐氏距離，由于核的代入，在原輸入空間中誘導出了一類核依賴的新的距離度量，由此將FCM在歐氏距離下的執行推廣到了同一空間中不同距離度量的新的聚類。

本文將式(6)中高斯核函數代入式(5)中，得到目標函數為

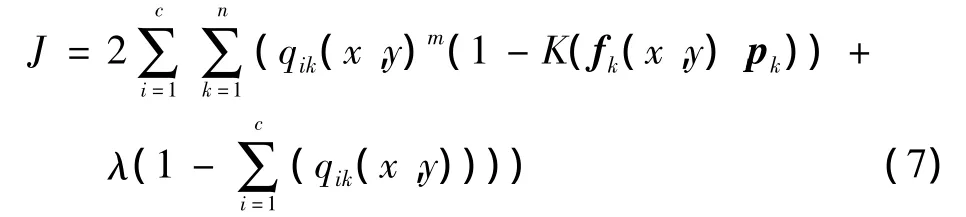
使用拉格朗日數乘法，首先對qk(x，y)m求偏導數，得到隸屬度迭代式

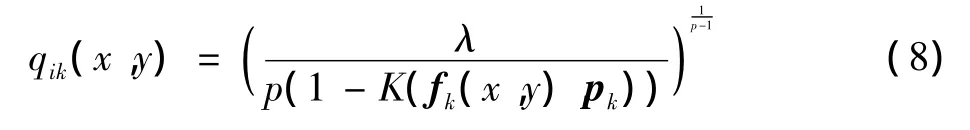
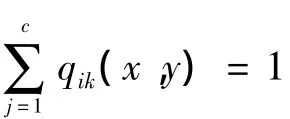
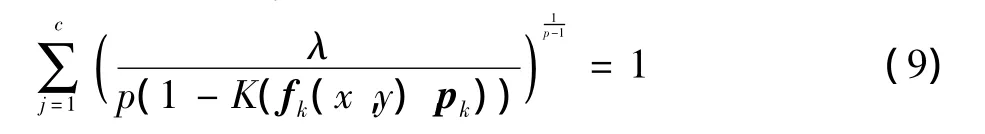
求出λ代入式(9)

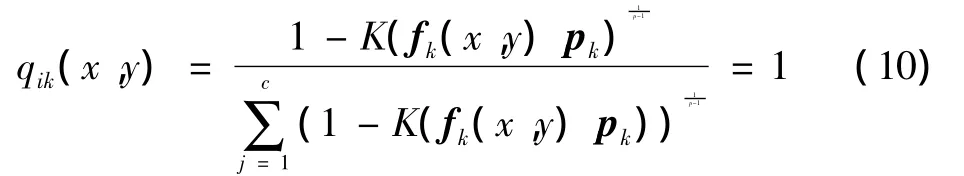
利用高斯核函數，代入高斯核函數，則目標函數變為

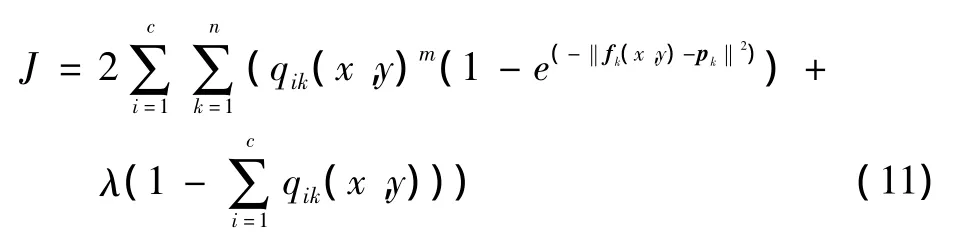
可以解得聚類中心迭代表達式

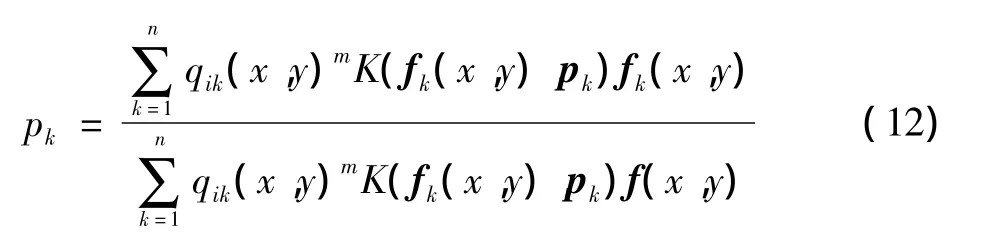
2.3 加入空間約束信息

對圖像進行非線性高維聚類劃分后，通過表征空間鄰域像素對初始聚類中心作用的先驗概率來修正各像素樣本的聚類劃分，形成最終修正的分割效果。利用Chuang Keh-Shih的研究成果，對已完成高維非線性空間核聚類劃分后并進行數據約簡的圖像進行空間鄰域隸屬度約束處理。劃分后的鄰域信息為

式中:NB(fj(x，y))表示像素fj(x，y)的領域大小;qim(x，y)表示像素fm(x，y)屬于i類的隸屬度值。Hik的值是除了當前空間像素領域區域內其他像素屬于i類的隸屬度和。經過鄰域隸屬度約束修正后的隸屬度的迭代表達式為

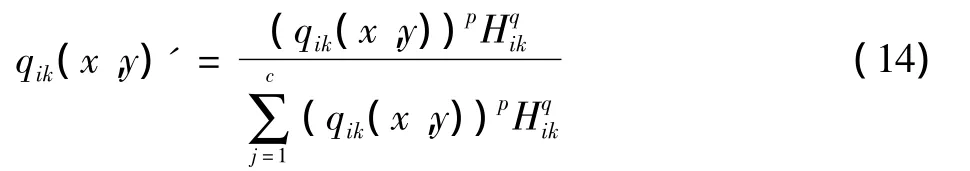
式中:p，q是正則化參數，用于控制最終隸屬度值的控制參數。式(14)表示鄰域空間中某一類的像素和其空間鄰域中像素同屬于一個類時Hik的值就越大，對原始隸屬度的修正就越大，反之則像素隸屬度值就減小。最終本文的分割算法過程步驟如下:

1)選擇聚類有效性指標計算方法，設置模糊系數m，設定聚類個數的最小值cmin、最大值cmax。

2)采用本文2.1節的方法得到約簡后的數據集合Nc={n1，n2，…nic}?Rs。

3)采用核估計方法實現聚類中心的估計，確定初始聚類中心。

4)再根據式(12)與式(10)分別計算或更新初始聚類中心和劃分矩陣。

5)利用式(14)修正隸屬度原型模式。

6)判斷迭代次數達到事先設定的最大次數，達到迭代次數則停止，否則繼續迭代。

3 實驗結果分析

為驗證本文所提算法的有效性，對正常大腦磁共振圖像進行實驗。初始參數設置:矩陣指數m=2，單步最小變化為0.000 5，最大迭代次數為100，聚類類別數為8，核參數均為150。參與比較的算法為原始的模糊C均值聚類算法、PSOFCM算法、KFCM算法、DWKFCM和本文算法，所有算法收斂精度相同且為ε，其他參數按原有文獻設定，運行20次取平均值。

為了驗證幾種分割算法的量化比較，采用合成圖像的分割精度和運行時間均值作為分割評價指標，定義合成圖像的分割精度為

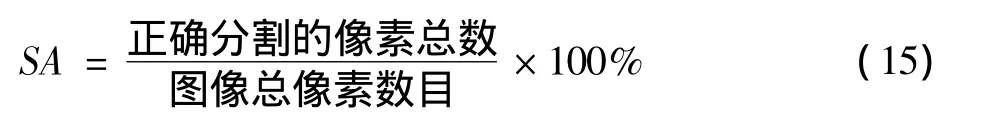
圖1為FCM算法、PSO_FCM算法、KFCM算法、DWKFCM算法及本文算法分割后圖像與本文算法的比較結果。

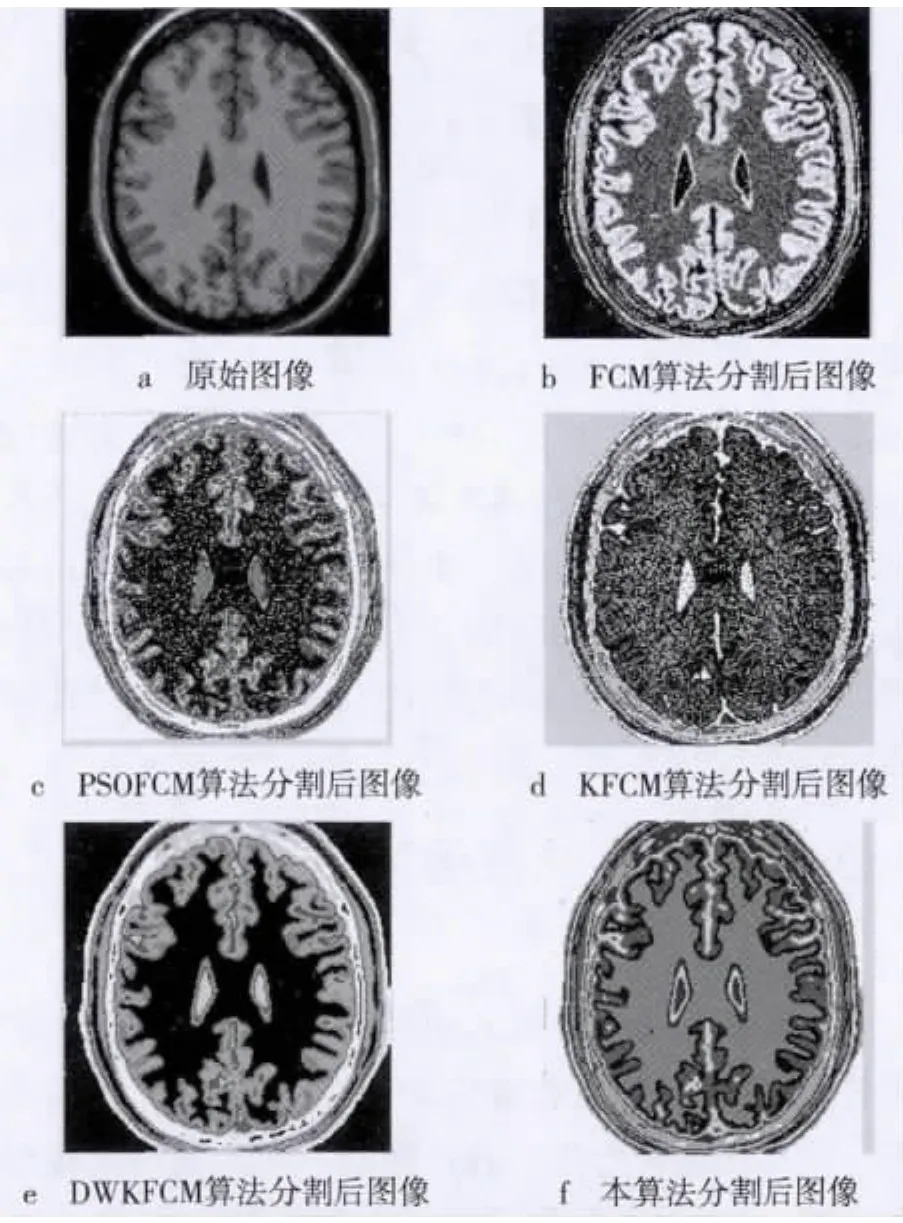
圖1 大腦磁共振圖像分割結果對比圖

圖1a為是一幅181×181像素的大腦磁共振圖像，圖1b為原始FCM算法，圖像分割效果有些模糊，一些細節還沒有分割出來，圖1c分割效果對比FCM算法稍好，但在中間部位的信息有一定的丟失。可以看出，本算法分割效果不錯，不但誤分割很少，且分割的腦灰質和腦白質邊緣也很光滑，在傳統模糊核聚類算法與動態加權模糊核聚類算法的分割結果里，都有較多的腦白質被誤分為腦灰質和腦脊液，同時分割的目標邊緣也毛糙;減小了過度分割的現象，又保留了圖像的細節部分，圖像中的主要目標較為準確、清晰地分割出來。

圖2是FCM、KFCM、DWKFCM和本文算法四種算法對圖1a進行分割時的算法收斂次數對比圖。從圖2可以看出，本文算法收斂次數很少，在很短時間內就能找到目標函數的最小值，具有明顯的速度優勢。

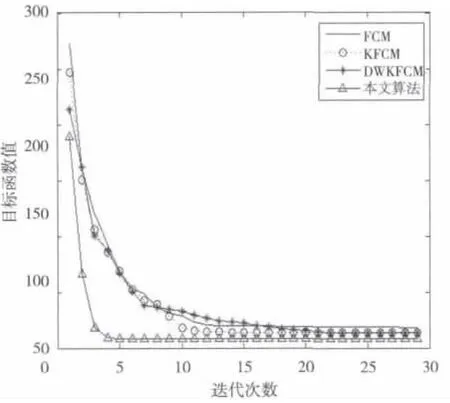
圖2 幾種算法的目標函數收斂對比圖

表1為FCM、PSOFCM、KFCM、DWKFCM和本文算法的性能比較結果。

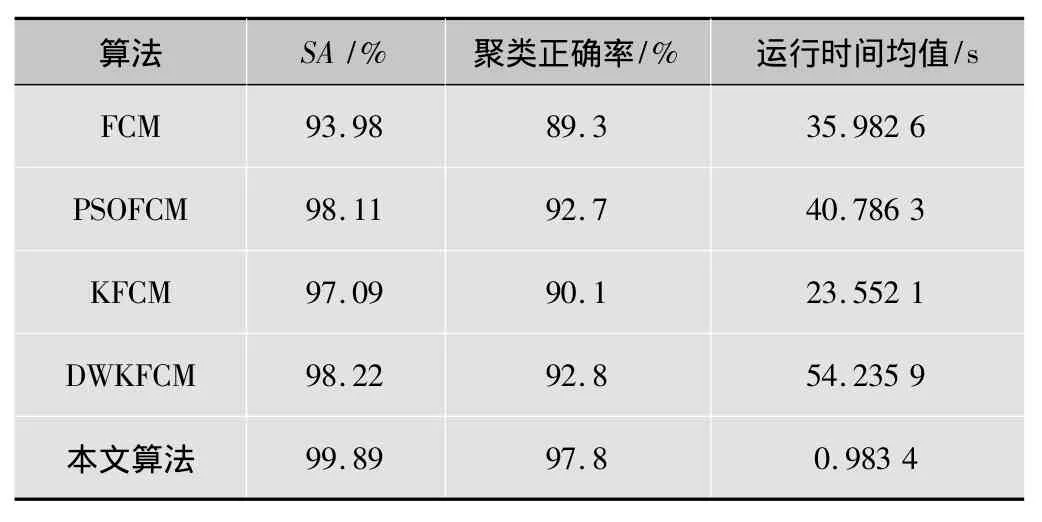
表1 幾種算法性能比較表

從表1可以看出，在同一迭代次數處，本文算法從圖像分割精度和運行時間上都大大高于其他幾種算法，實驗表明本算法具有較好的適應性和魯棒性。

4 結束語

針對傳統模糊核聚類算法存在的問題，本文將數據約簡技術與模糊核聚類算法相結合提出一種新的算法，先通過數據約簡大幅度降低數據個數，節省計算時間;然后在FCM算法中利用核函數將約簡后的數據映射到非線性高維空間中進行聚類劃分;最后使用像素點的空間鄰域信息修正當前像素空間的隸屬度值，得到更加準確的聚類結果。改進的受空間約束的模糊核聚類算法簡單且運算速度更快，再結合空間鄰域信息修正當前像素的隸屬度值，得到更加準確的聚類結果。實驗結果表明，該算法具有較好的分割圖像質量，相比其他幾種圖像算法有更快的分割速度及更準確的分割精度，表現出了較強的魯棒性和較好的工程價值。

:

［1］劉剛，梁曉庚，張京國.基于輪廓波變換和改時模糊C均值聚類的紅外圖像分割［J］.系統工程與電子技術，2011，23(2):443-448.

［2］曲福恒.一類模糊聚類算法研究及其應用［D］.長春:吉林大學，2009.

［3］CHUANG K，TZENG H，CHEN S，et al。Fuzzy C mean clustering with spatial information for image segmentation［J］.Elsevier Science，2006(30):9-15.

［4］楊潤玲，周軍妮，劉利.基于改進型FCM聚類的圖像分割新方法［J］.電視技術，2008，32(6):12-14.

［5］丁震，胡鐘山，楊靜宇，等.FCM算法用于灰度圖像分割的研究［J］.電子學報，1997，25(5):39-43.

［6］匡泰，朱清新，孫躍.FcM算法用于灰度圖像分割的初始化方法的研究［J］.計算機應用，2006，26(4):784-786.

［7］高新波.模糊聚類算法的優化及應用研究［D］.西安:西安電子科技大學，1999.

［8］龐冬冬，史健芳.基于改進主動輪廓模型的圖像分割算法［J］.電視技術，2013，37(1):41-44.

［9］WANG S.A new integrated clustering algorithm GFC and switching regressions［J］.Int.J.Pattern Recognition and Artificial Intelligence，2002，16(4):433-447.

［10］GOKCAY E，PRINCIPE J.Information theoretic clustering［J］.IEEE Trans.PAMI，2002，24(2):158-171.