一種球頭銑刀“S”形刃口曲線的數學建模方法*

龐思勤，喬小峰，王西彬，彭 松

(北京理工大學 先進加工技術國防重點學科實驗室，北京 100081)

由于球頭立銑刀加工復雜曲面時有較好的自適應性和減振性，可以十分方便地加工模具內腔型面以及其他復雜曲面，廣泛應用于加工自由曲面機械構件、模具等產業[1].同時，由于刀刃曲線一般為變導程弧形曲線且經過回轉軸線，球頭立銑刀具有切削力小，波動范圍不大，耐用度高，切削過程平穩等優點[2].除此之外，球頭立銑刀的切削性能和加工質量在很大程度上也取決于刀刃曲線的合理設計[3].早期的刀刃曲線以直線刃為主，隨著工件加工精度要求的提高，隨后便出現了一般曲線刃和螺旋線刀刃.目前，對“S”形刃口曲線的研究和應用較廣泛，有關“S”型刃口曲線設計和優化方法的文獻層出不窮，易德明等人在分析球頭立銑刀刃磨方法的基礎上，建立了“S”形刃球頭立銑刀的前、后刀面及切削刃的數學模型[4].廖鋼等人對“S”形刃球頭立銑刀幾何參數進行了分析與優化，并對切削機理進行了研究[5].胡思節等人根據球頭立銑刀的刃磨參數所需滿足的條件，對“S”形刃口曲線進行了數學建模[6].汪云濤等人在已建立球頭銑刀前刀面和后刀面數學模型的基礎上，研究了“S”形刃口球頭銑刀的誤差數學模型[7].Lee等人提出在球頭銑刀球面部分，以一個與刀軸垂直的圓柱面與之相交而形成的“S”形刃口曲線模型[8].Tai等人使用多項式構造了“S”形刃口曲線模型[9].盛尚雄等人根據加工時前刀面的成形運動,分別研究了圓柱和圓錐球頭立銑刀球頭部分的“S”形刃口曲線數學模型[10].Lin等人討論了“S”刃口球頭銑刀的制造問題[11].

由于球頭銑刀在切削加工時的點接觸狀態會使加工效率降低，隨著五軸數控機床的廣泛引入，球頭銑刀在某些加工領域已被側銑刀所代替.但是，為了降低生產成本，二軸及三軸數控機床加工過程中仍然廣泛使用球頭銑刀，對球頭銑刀的深入研究是有必要的.目前，對球頭銑刀“S”形刃口曲線的研究較為廣泛，但是對球面與多個平面相交而成的刀刃曲線數學建模問題的研究少之又少.本文在推導文獻[12]中提到的“S”形刃口曲線的過程中，結合空間幾何理論和微分幾何理論，首次提出了“單球法”和“雙球法”兩種數學建模方法，可以應用于球頭銑刀球面與兩個成一定夾角空間平面相交所形成的“S”形刃口曲線的數學模型推導問題，也可以應用到多個空間平面與球面相交的問題.

1 球面刀刃曲線通用數學模型

如圖1所示，設點M為球頭銑刀刀刃曲線上任意一點，刀刃曲線方程為：

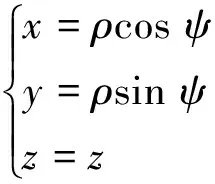
(1)

式中ρ為M點處矢徑，ψ為相對于zox平面的偏轉角，顯然，其均為z的函數，即有：ρ=ρ(z),ψ=ψ(z).據此可以求出刀刃曲線上M點處的單位切矢量τ，回轉面輪廓母線在M處的切矢量τ0和輪廓表面在M點處的單位法矢量n0分別為：

τ=

(2)

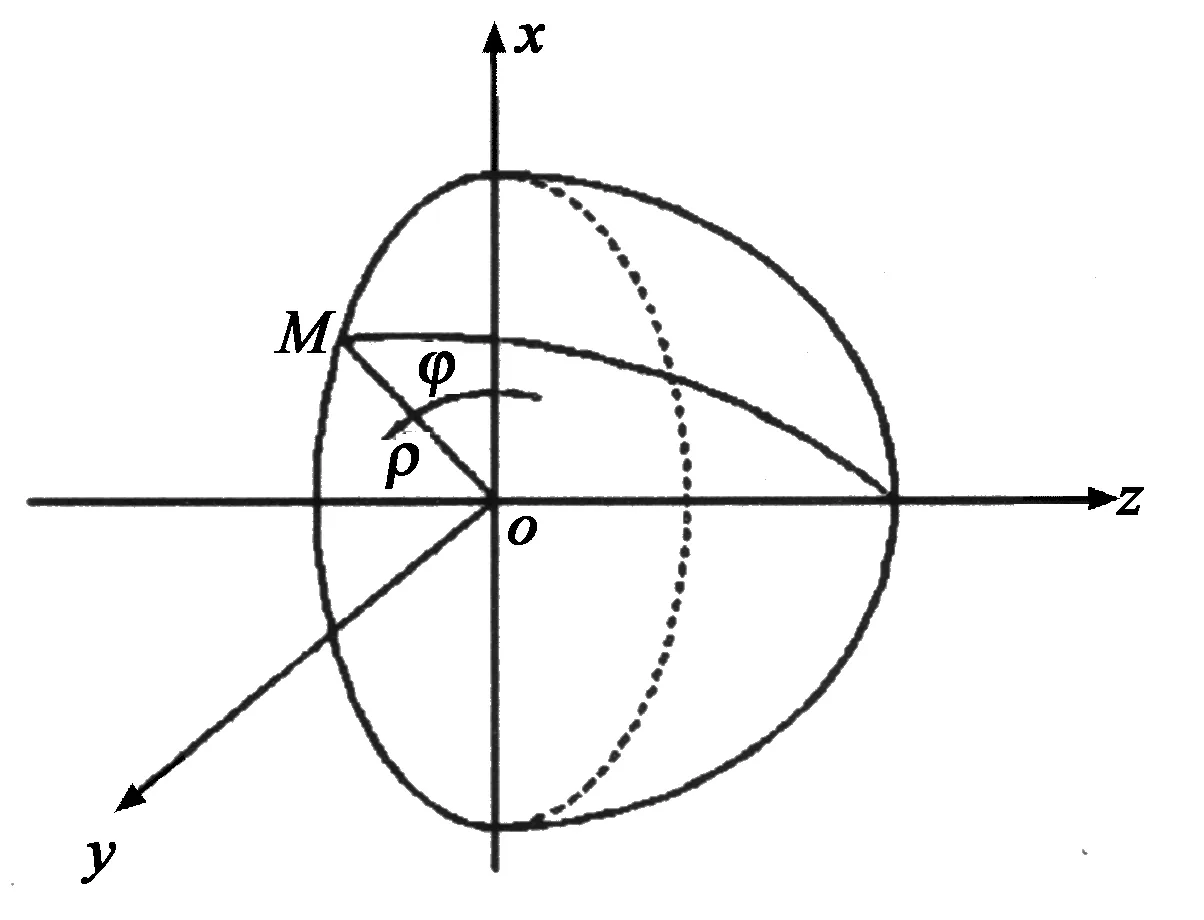
圖1 球面“S”形刃口曲線

由于錐面為回轉面，所以在其經線上dψ/dz=0，代入式(2)可得：

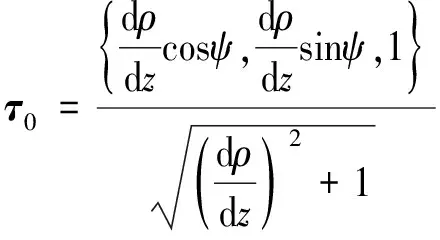
(3)

n0=τ×τ0

(4)

根據螺旋角的定義，刀刃M點處螺旋角為單位切矢量τ和τ0之間的夾角，即

cosβ=τ·τ0

(5)

將式(2)，(3)代入式(5)，得到偏轉角的微分方程表達式：

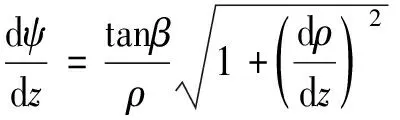
(6)

由式(6)解得ψ并代入式(1)，便可求得球面刀刃曲線參數方程如式(7)所示:

(7)

2 球面上平面刀刃曲線的簡化數學模型

在刀刃曲線設計過程中，為使刀刃過銑刀回轉軸，球面部分采用復合型切削刃，即在刀尖點附近，采用平面曲線刀刃，而在遠離刀尖點的部位，采用能與平面曲線刀刃光滑連接的刀刃曲線，通常為螺旋線刀刃曲線，也可以為不同平面上的刀刃曲線，本文主要對兩個不同平面上的兩段平面刀刃曲線進行數學建模.

如圖2(a)所示，平面Ⅰ，Ⅱ相交于球的一條直徑線，在平面Ⅰ內過直徑線的一個端點作球面的切線t，過切線t作另一個平面Ⅲ，平面Ⅱ，Ⅲ和球面相交于球面上一點M，球面角β即為平面刀刃曲線上任意一點M處的螺旋角，平面Ⅰ，Ⅱ之間的夾角即為平面刀刃曲線上任意一點M處的偏轉角ψ的余角.

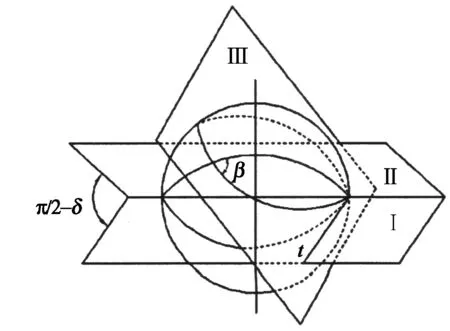
(a)點M處偏轉角和螺旋角關系圖

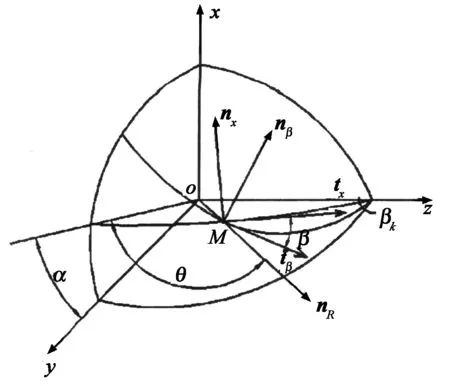
(b)點M處矢量圖

如圖2(b)所示，平面Ⅱ，Ⅲ和球面的相交點M坐標、M點在球面上的法矢量nR、平面Ⅱ的法線矢量nx和平面Ⅲ的法線矢量nβ分別如式(8)～(11)所示：

(8)

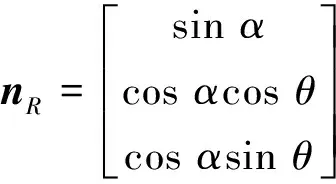
(9)

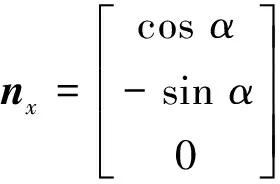
(10)

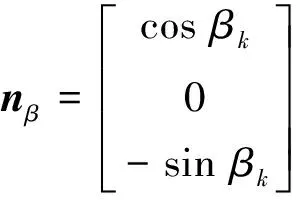
(11)

式中R為球面半徑；α，θ為球面參數；βk為平面與z坐標軸的夾角，且有：

(12)

平面Ⅱ和球面的交線與平面Ⅲ和球面交線在相交點M處的切向量為tx和tβ：

tx=nx×nR，tβ=nβ×nR

(13)

由平面Ⅱ和平面Ⅲ在球面上的球面角β的定義，可得：

(14)

將式(9)、(10)和式(11)代入式(13)，得：

即，用過球面直徑線端點的切線作任一平面Ⅲ，平面Ⅲ和球面的交線與過同一端點的球面經線所形成的球面角β，與過球面經線的平面Ⅱ和過直徑線端點切線的平面Ⅰ相交于直徑線所形成的二面角α在數值上相等，如圖2所示.如圖1中所示，設平面Ⅰ為yoz坐標平面，平面Ⅰ，Ⅱ相交所得直徑線為z坐標軸，則平面Ⅲ和球面的交線為球頭銑刀刀刃曲線，球面角β為刀刃曲線上任意一點M處的螺旋角，二面角α為點M處偏轉角的余角，即：

(15)

聯立式(12)，(15)，便可求得刀刃上任意一點M處的偏轉角為：

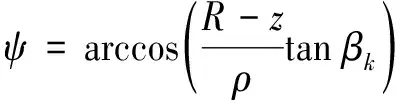
(16)

將式(16)代入式(1)，得球面上簡化的平面刀刃曲線的參數方程如式(17)所示：

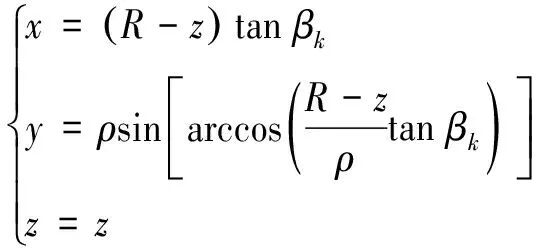
(17)

對比式(17)和式(7)，可以明顯看出刀刃曲線方程得到了有效簡化，更易于求解.

3 一種“S”形刃口曲線的數學模型

3.1 新型“S”形刃口曲線特征

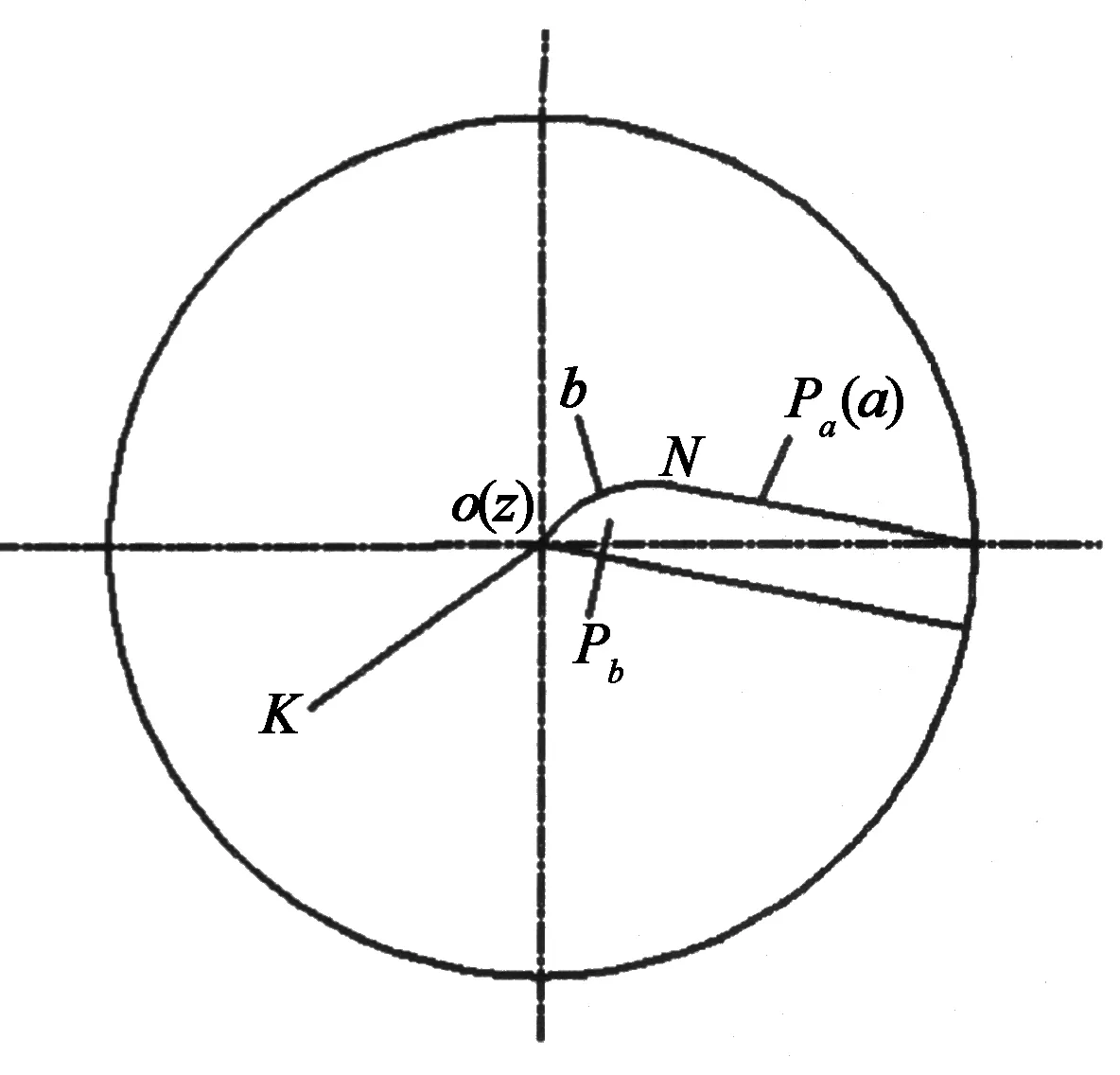
本文應用簡化的平面刀刃曲線的參數方程，對文獻[12]提出的球頭銑刀“S”形刃口曲線進行數學建模.如圖3所示，該球頭銑刀的刃型特點有以下特征[12]：

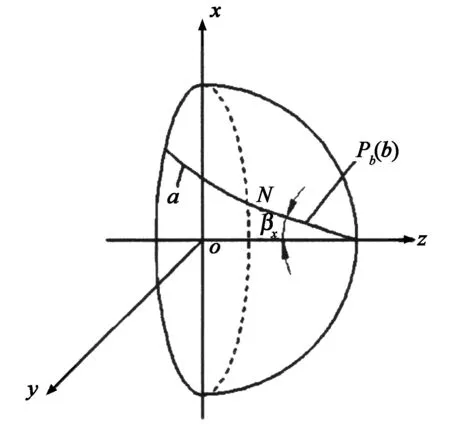
1)刃型曲線由平面Pa與球面的交線和平面Pb與球面的交線組合而成，即由圖3所示的兩段平面圓弧a和b組成.圓弧b的一端與圓弧a相切于點N，另一端與半球面沿刀具回轉軸線方向的頂點K(刀尖)重合.

2)平面Pb與圓弧刃a段的后刀面相切，切線通過圓弧a和b的切點N.

3)b段圓弧刃的前刀面為圓柱面，并與Pb相切.

4)圓弧a和b所在的平面Pa和Pb分別與刀具軸線不平行也不垂直.平面Pa為a段圓弧刃的前刀面，平面Pb為b段圓弧刃的后刀面.

3.2 “單球法”和“雙球法”理論

本文基于簡化的球頭銑刀平面刃口曲線數學方程和圖3所示球頭銑刀球面部分刃口曲線幾何特征，首次提出了“單球法”和“雙球法”的理論方法，基于此方法可以解決球頭銑刀球面部分任意數量和任意位置平面與球面相交而成的刃口曲線數學建模問題.

(a)“S”形刃口曲線平面視圖

(b)“S”形刃口曲線三維視圖

圖4 平面位置關系圖

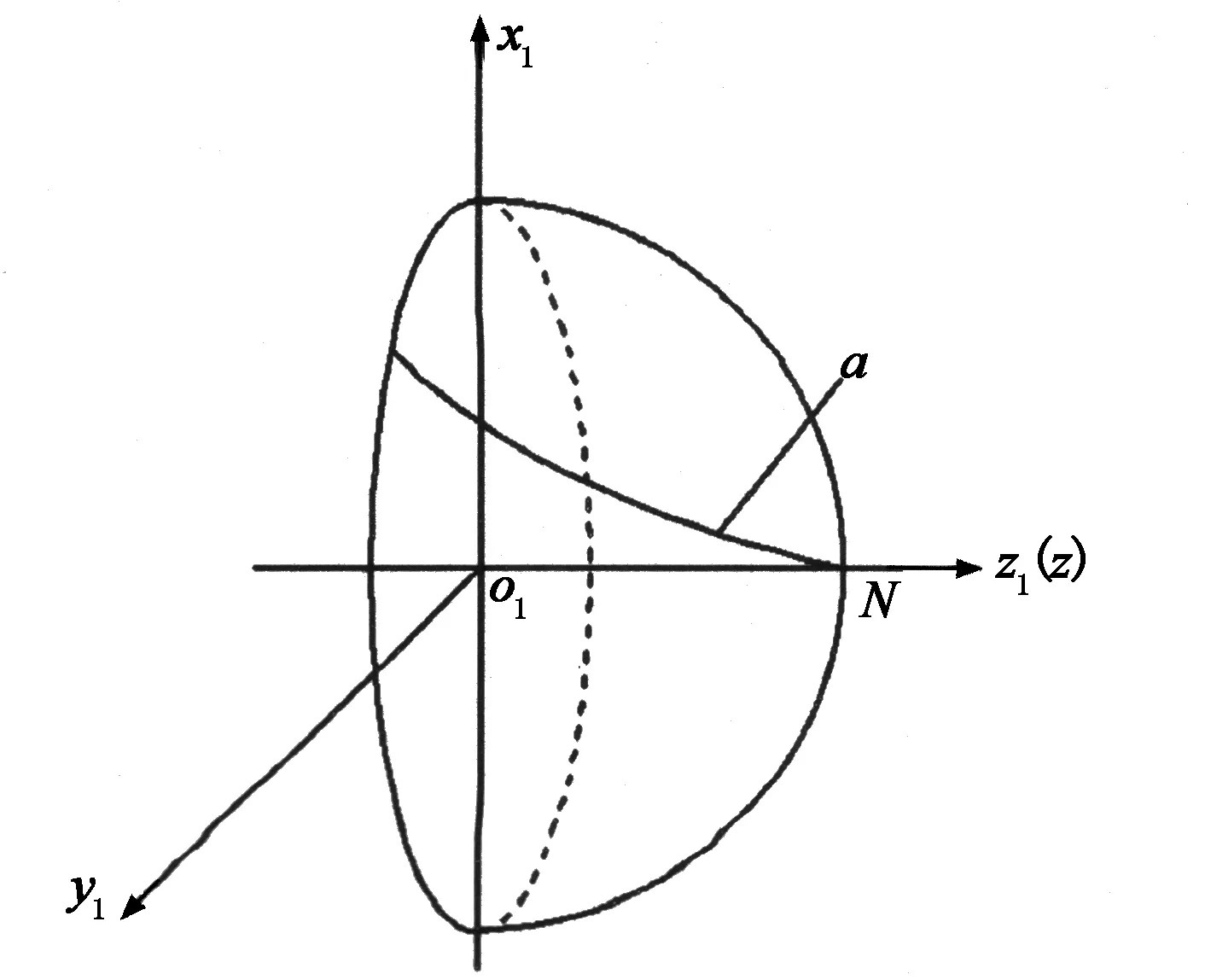
同樣，“雙球法”是在不同球面上或不同坐標系中對兩段或多段平面刃口曲線進行數學建模，兩球面半徑須相等.如圖5所示，平面Pa位置不變，建立能使平面Pa滿足上述條件的過渡坐標系o1x1y1z1，將平面參數代入式(17)可求得過渡坐標系o1x1y1z1中a段刃口曲線的數學模型，對過渡坐標系o1x1y1z1進行坐標變換使其與坐標系oxyz重合，求得過渡坐標系變換為固定坐標系的變換矩陣，對過渡坐標系中的刃口曲線進行同樣的坐標變換，即可求得a段刃口曲線在坐標系oxyz中的數學模型，可歸納為：建立過渡坐標系→滿足條件→過渡數學模型→坐標變換→數學模型.

3.3 “單球法”建立平面刃口數學模型

3.3.1 平面Pb與球面相交刃口曲線方程

如圖3所示，b段刃口曲線由平面Pb和球面相交而成，平面Pb與y平行，符合式(17)推導條件.將平面Pb和z坐標軸夾角βk代入式(17)，可得b段刃口曲線數學模型如式(18)所示：

(a)a段刃口曲線圖

(b)平面Pa位置坐標圖

(18)

3.3.2 平面Pa與球面相交刃口曲線方程

(19)

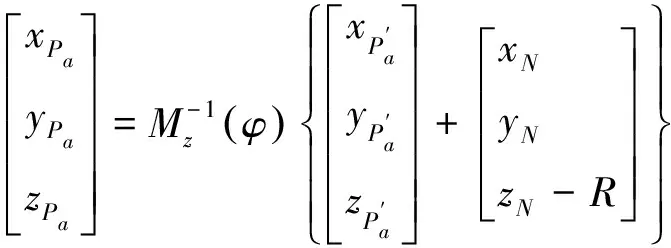
式中Mz(φ)為平面Pa繞坐標軸z旋轉角度φ時的變換矩陣，如式(20).xN，yN，zN為刀刃曲線連接點N在坐標系oxyz中的坐標值.

(20)

(21)

將式(18)，(20)代入式(19)便可得平面Pa在同一坐標系oxyz中的刀刃曲線方程如式(22)所示:

(22)

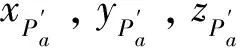
(23)

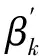
3.4 “雙球法”建立平面刃口數學模型

本文提出的“雙球法”，即以N點為球面直徑線端點，在坐標系o1x1y1z1中建立一個等半徑的球面，z1軸和z軸在空間坐標系中平行，如圖5所示.平面Pa與坐標軸y1平行，且與z1坐標軸之間的夾角為β1，符合式(17)推導條件，由此可得a段刃口曲線在o1x1y1z1坐標系中的數學方程如式(24)所示:

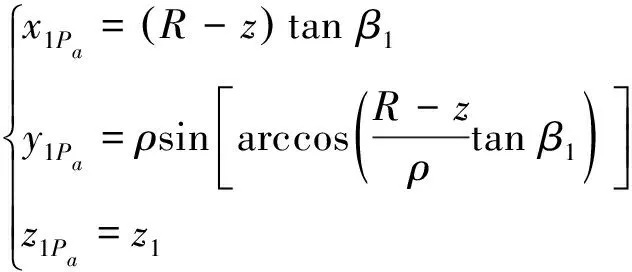
(24)

式中x1Pa，y1Pa，z1Pa分別為a段刃口曲線上任意一點在o1x1y1z1坐標系的坐標值.

將式(24)所示刃口曲線方程通過坐標變換轉換到oxyz坐標系中，即可得到a段刃口曲線在oxyz坐標系中的數學方程如式(25)所示:

(25)

由式(18)和式(25)可得球面上平面刀刃曲線方程為：

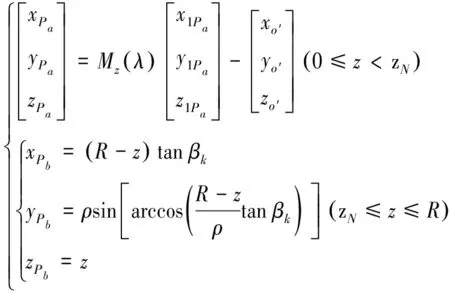
(26)

式中Mz(λ)為平面Pa繞坐標軸z旋轉角度φ時的變換矩陣，如式(27).xo′，yo′，zo′分別為坐標原點o1在坐標系oxyz中的坐標值.zN為a,b兩段刃口曲線連接點N的坐標值，可由Pa和Pb平面參數βk和β1確定.

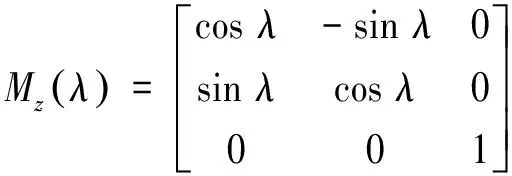
(27)

4 結 論

本文通過對空間平面理論和球面相交理論進行推導的基礎上，證明了球面部分平面刃口曲線偏轉角和螺旋角相等的簡明數學關系，簡化了球面部分平面刃口曲線的數學模型.同時，應用本文提出的“單球法”和“雙球法”數學建模方法，并結合簡化的平面刃口曲線數學模型，對一種新型“S”形刃口曲線進行了數學建模，應用此建模方法可以求解球頭銑刀不同數量空間平面與球面相交所形成的刃口曲線方程，既降低了平面刀刃曲線推導過程的復雜性，同時又為兩個或多個空間平面與球頭銑刀球面部分相交而成的復合型刃口曲線方程的數學建模提供了一種有效方法.

[1]HSIEH J F,WANG F S .Mathematical modeling of ball-end cutter[J].Applied Mechanics and Materials,2013,284/287 (1):806-809.

[2]董敏，唐余勇，董增福.關于球頭銑刀的等螺距連續刃口曲線 [J].哈爾濱工業大學學報,2003,35(3)：301-303.

DONG Min,TANG Yu-yong,DONG Zeng-fu.Continuous blade curve of isobaric pital of spherical milling cutter[J].Journal of Harbin Institute of Technology,2003,35(3):301-303.(In Chinese)

[3]何耀雄，周云飛，周濟.球頭刀具刃形建模與過渡刃設計[J].機械工程學報，2001，37(9)：30-35.

HE Yao-xiong,ZHOU Yun-fei,ZHOU Ji.Blade modeling and transitional blade design of spherical milling cutter[J].Chinese Journal of Mechanical Engineering,2001,37(9):30-35.( In Chinese)

[4]易德明，廖鋼，龍美彪.“S”形球頭立銑刀的研究(Ⅰ)—數學模型[J].湖南大學學報,1996,23(2):65-69.

YI De-ming,LIAO Gang,LONG Mei-biao.Research on the ball-nose end mill with “S” shape major cutting edges(Ⅰ):A mathematical model[J].Journal of Hunan University,1996,23(2):65-69.(In Chinese)

[5]廖鋼,龍美彪.“S”形球頭立銑刀的研究(Ⅱ)—幾何參數分析[J].湖南大學學報,1996,23(4):111-115.

LIAO Gang,LONG Mei-biao.Research on the ball-nose end mill with “S” shape major cutting edges(Ⅱ):Geometric parameter analysis[J].Journal of Hunan University,1996,23(4):111-115.(In Chinese)

[6]胡思節，廖剛，易德明.“S”形球頭立銑刀的研究(Ⅲ)—刃磨參數分析[J].湖南大學學報,1996,23(6):71-77.

HU Si-jie,LIAO Gang,YI De-ming.Research on the ball-nose end mill with “S” shape major cutting edges(Ⅲ):Analysis of grinding parameters[J].Journal of Hunan University,1996,23(6):71-77.(In Chinese)

[7]汪云濤，鮑青山，唐余勇.“S”形刃口球頭銑刀加工的誤差分析[J].制造技術與機床，2002(8):34-36.

WANG Yun-tao,BAO Qing-shan,TANG Yu-yong.Analysis on error for machining “S”-shaped-edge ball nose milling cutter[J].Manufacturing Technology and Machine Tools,2002(8):34-36.(In Chinese)

[8]LEE P,ALTINTAS Y.Prediction of ball-end milling forces from orthogonal cutting data [J].Int J Mach Tools Manufact,1996,36(9): 1059-1063.

[9]TAI C C,FUH K H.Model for cutting forces prediction in ball-end milling [J].Int J Mach Tools Manufact,1995,35(4): 511-524.

[10]盛尚雄,吳卓,馬世輝.S形刃球頭立銑刀的數學模型 [J].甘肅科學學報,2009,21(4): 104-107.

SHENG Shang-xiong,WU Zhuo,MA Shi-hui.Mathematical model of ball-end cutter with “S” shape[J].Journal of Gansu Science,2009,21(4): 104-107.(In Chinese)

[11]LIN P D,LEE M F.NC data generation for 4-axis machine tools equipped with rotary angle head attachments to produce variable pitch screws [J].Int J Mach Tools Manufact,1997,37(3): 341-353.

[12]師潤平.一種空間曲線刃球頭銑刀的設計[J].工具技術,2008,42(6):76-79.

SHI Run-ping.Design of ball end mill of shape curve cutting edge[J].Tool Technology,2008,42(6):76-79.(In Chinese)