多域邊界面法在穩態熱傳導問題中的應用*

張見明，李湘賀，陸陳俊，李光耀

(湖南大學 汽車車身先進設計制造國家重點實驗室,湖南 長沙 410082)

計算機輔助工程(CAE)對于推動產品研發具有重大的意義.目前CAE的發展已比較成熟，許多成熟的商業CAE軟件正在被廣泛地采用.但CAE仍面臨許多難題[1]，比如如何離散復雜幾何的單元才能進行有效計算，如何處理大規模工程問題的數值計算.陸續涌現出的有限差分法(FDM)、有限體積法(FVM)、有限元法(FEM)和邊界元法(BEM)[2]都未能很好地解決這些問題.而目前大多數CAE軟件采用的是有限元法.

有限元法需要對整個求解域進行離散，將會產生一個很大的代數方程組.對于求解三維(3-D)復雜的實體，尤其是含有細小特征時，離散為可以進行有效計算的實體單元往往比較困難.并且，有限元法的實現基于所求物理問題控制方程和邊界條件的等效積分“弱”形式，其試函數要求至少具有一階連續性.導致應力精度總是比位移精度低一階，但在實際問題中更關注于應力值，比如產生應力集中的部位及其最大值.

相較于FEM，邊界元法(BEM)[3]彌補了有限元法的不足，是一種更加有效的數值方法.它具有等幾何分析的特點，使其便于模擬復雜的幾何形狀.邊界元法基于邊界積分方程，只需對求解模型的邊界進行離散，使求解的問題域降低了一級，大大簡化了分析和計算.并且邊界積分方程采用問題的解析基本解，具有更高的精度.然而，在傳統的邊界元法中，三維CAD幾何模型被離散成邊界元分析模型后，CAD模型的原始幾何信息基本被丟掉，這會從根本上導致計算精度的問題，有些甚至對計算起著決定性的作用，并且導致設計和分析成為了兩個相互獨立的過程.由于CAD模型和分析模型的分離，在邊界元自適應網格細分過程中，需要反復地與CAD系統進行交互，而每個交互的過程是很繁瑣的.

為了克服上述缺點，張見明教授在邊界元法[4]和邊界點法的基礎上，創造性地提出了邊界面法(BFM).在該方法中，對邊界的數值積分和場變量的插值都在邊界曲面的二維參數空間中進行，CAE分析是直接在CAD模型上進行的，實現了復雜結構的CAE分析自動化.由于CAE模型與CAD幾何模型融為了一體，不管網格離散有多么粗糙，分析模型在幾何上都是精確的.并且，自適應網格細分過程中,不需要再與CAD系統反復地進行交互,使自適應分析變得簡單.

目前邊界面法已經取得了許多研究成果，覃先云等人開發了一套參數曲面內網格自動生成的算法[5]，使BFM向實際工程應用邁出一大步.在覃先云的方法中，單元定義和網格的劃分都在邊界表面的參數空間中進行.谷金良等人提出在BFM中用B樣條插值方案來做物理變量的近似[6-8]，并將其成功地應用于穩態熱傳導問題和彈性靜力學問題，并且通過在幾何模型中采用相同的插值方案，谷金良等人實現了邊界面法的等幾何分析.莊超等人實現了基于幾何模型的BFM[9]，其幾何模型通過細分曲面成型技術構建.謝貴重等人通過引入改進的距離變換、指數變換，提出了一套高效的近奇異積分計算方案[10]，解決了薄型結構分析精度下降的問題.張見明等人通過快速多級子算法、自適應交叉擬合(ACA)和分級矩陣(H-matrix)技術，成功地將計算量級從O(N2)降至O(NlogN)，并且基于GPU高性能并行計算，在CUDA編程環境中實現邊界面法正則積分的并行加速[11]，使邊界面法的大規模工程應用成為可能.

以上所提及的邊界面法的應用，都是基于單域模型.然而，在工程實際分析中，往往存在許多復雜的結構，這些結構需要被分割成多個子域.本文將邊界面法的應用延伸至多域模型的穩態熱傳導問題.在多域問題中，矩陣的組裝是至關重要的，文中以3個兩兩相交的域為例，給出矩陣組裝的過程.然后，以某大壩為例，按照大壩的真實施工過程、施工參數和現場實驗所得的材料參數，并查閱資料，進行仿真分析，研究壩體的溫度分布狀況，給出大壩采用多域邊界面法進行穩態熱傳導計算的數值結果，并和有限元法(采用Abaqus軟件)的結果進行對比.

1 三維穩態熱傳導問題的邊界面法

1.1 邊界積分方程

三維穩態熱傳導問題可用如下表示：

u,ii=0,?x∈Ω

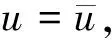
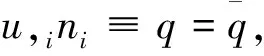
(1)

把上述問題轉化為等效邊界積分形式：

(2)

式中y,s分別為邊界上的源點和場點；q=?u/?n代表邊界法向流量；us(s,y) 和qs(s,y) 代表相應的基本解，它們分別滿足：

us,ii=δ(y,s),?s∈Ω

(3)

qs=?us/?n(s)

(4)

對于三維問題，

(5)

其中r是源點和場點之間的距離.

1.2 邊界積分方程的離散

本節介紹一種基于表面單元的Lagrange近似.面單元定義在表面的二維參數空間而不是在物理空間或者其他的參數空間，這樣所考慮的邊界積分的幾何數據可以通過參數轉換直接進行計算，這樣的參數變換與參數空間的映射方案相同.換言之，可以精確得到積分中的幾何信息.下面以四節點四邊形單元為例(如圖1所示)，進行物理變量的近似.

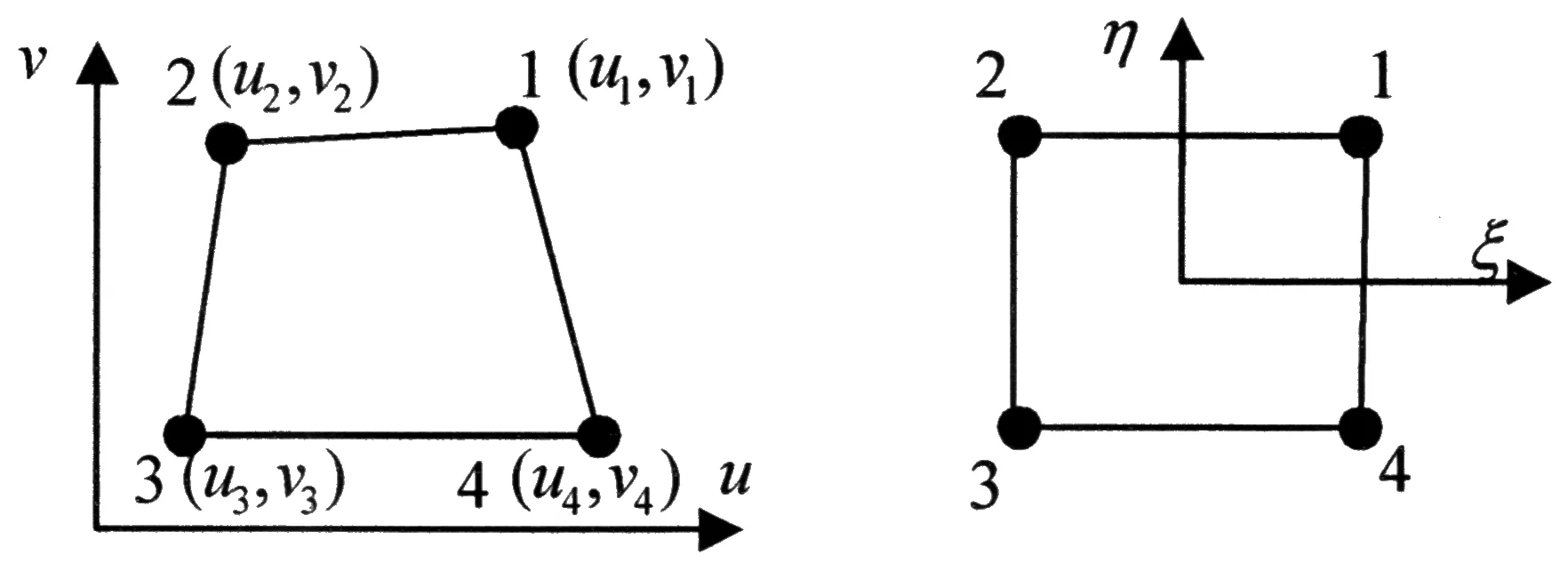
圖1 四節點面單元及其坐標變換

在這里構建的形函數如下：

(6)

這些形函數只用于邊界表面上的物理變量的近似，幾何數據保持精確值，這是和傳統邊界元法的主要區別.

(7)

其中x=x(u,v),y=y(u,v),z=z(u,v),uk和qk分別是邊界節點上的溫度值和法向流量，N為所有插值點的個數.采用這樣的近似方案后，邊界積分方程(2)離散為：

Nk(y))ukdΓ(s)=0

(8)

把場點分布到每一個插值點后，邊界積分方程可組裝成：

Gq-Hu=0

(9)

其中

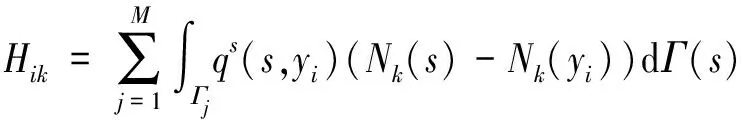
(10)

(11)

上式中，Γj為形函數Nk(s)值不為0的邊界單元，數量記為Num.

將方程(9)進行變換，使未知量移到左邊，已知量移到右邊，形成線性組，

AX=b

(12)

式中X是uk或qk的未知數向量.求解方程(12)，就可以得到所有節點k(k=1,2，…，N)上未知量uk或qk的值.根據節點上的值，相應地可以求得邊界上和域內任意一點的勢和流量值.

2 多域邊界面法在三維穩態熱傳導問題中的應用

本章首先介紹單域問題的矩陣組裝，然后仿照單域問題和文獻[12]，推導穩態熱傳導問題的多域邊界面法的邊界積分方程及其矩陣組裝.由于給定第一類(溫度、位移)或者第二類(熱流密度、面力)邊界條件時矩陣的組裝較容易，這里我們只介紹含有對流邊界的矩陣組裝方法.

2.1 單域穩態熱問題矩陣的組裝

單域問題的邊界積分方程為：

(13)

其中Hij,Gij分別為式(9)中的矩陣塊，上式可寫為：

(14)

令：

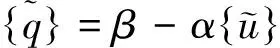
(15)

其中，

(16)

βi=-hu，αi=-h

(17)

組裝之后為：

(18)

2.2 多域邊界面法中矩陣的組裝

以3個兩兩相鄰的立方體為例，推導多域問題的邊界積分方程，如圖2所示．

圖2 3個兩兩相鄰立方體示意圖

在這個模型中，立方體1和立方體2的邊界相交于Γ12,立方體1和立方體3邊界相交于Γ13，立方體2和立方體3邊界相交于Γ23.兩個域相交處的溫度邊界和熱流密度邊界分別為：

(19)

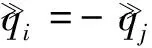
(20)

立方體1的邊界積分方程如式(21)所示：

(21)

其中，下標d,n,r分別表示第一個域溫度邊界、熱流密度邊界、對流邊界所對應的系數矩陣塊.下標2，3表示第一個域分別與第2、第3個域相交邊界所對應的系數矩陣塊.加入立方體1的邊界條件：

(22)

并且將式(15)代入式(21)，之后把未知量移到左邊，已知量移到右邊，可得：

(23)

類似立方體1，立方體2和立方體3也分別有如下重新組裝的邊界積分方程：

(24)

(25)

(26)

求解該方程組得到邊界上節點的溫度和流量，然后利用邊界積分方程(8)，取y為任意域內點，則得到域內任意點的溫度.再對邊界積分方程(8)兩邊同時求y點任意方向的導數，即得到y點在任意方向的流量值.由于這種方向求導不是對形函數而是對基本解求的，不會降低擬合精度，因此使得溫度和流量的結果具有同階的計算精度.

3 數值算例

本章分析圖3所示水壩結構在固定水溫及固定空氣溫度的邊界條件下，壩體內溫度的分布情況.

3.1 混凝土水壩模型

如圖3所示，考慮對稱性，模型厚度取為20 m.基巖高270 m，寬471 m.基巖上的壩體高度為171 m，不均勻地分為62層(與建設過程保持一致)，第一澆筑層底部與基巖接觸部分寬157 m.大壩模型左側為上游面，右側為下游面，上游面假設蓄水高度為375 m，距壩體最頂端9 m.

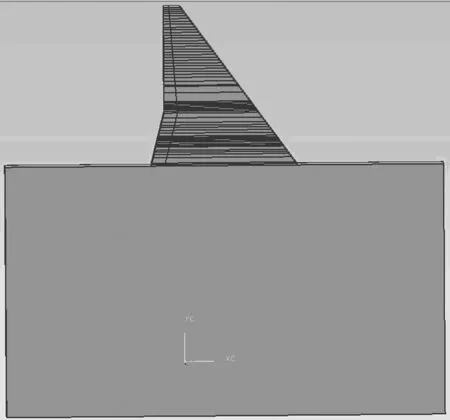
圖3 某重力壩段結構示意圖

3.2 大壩的材料參數

壩段建造采用兩種不同的混凝土材料：壩體最底端兩層采用常態混凝土，基巖材料視為與第一、二澆筑層相同，壩體其他層采用碾壓混凝土.材料參數見表1．

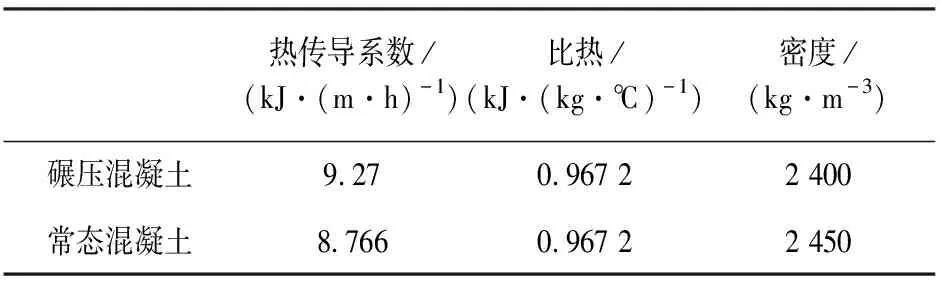
表1 大壩材料參數

3．3 邊界條件

基巖左右兩側及底部絕熱，模型厚度方向前后面絕熱.上游面375 m高度以上、頂部表面、下游面添加空氣邊界，當地年平均氣溫為20.7 ℃.上游面蓄水區添加水溫邊界條件，其中水溫邊界如下：

1)水溫在深度0～123.4 m隨深度擬合為線性變化，其擬合函數為：

Tw=20.7-0.059 157 2×h

(27)

2)在距水面123.4 m以下，溫度取深水溫度13.4 ℃.

3.4 網 格

為做對比分析，除了使用邊界面方法分析之外，還采用基于有限元方法的商用軟件ABAQUS 11.0對此結構進行穩態熱分析，由于本模型中大壩每層的厚度較薄，因此網格較密.在分析過程中一共使用了47 432個二次六面體單元，共計272 300個計算節點，網格模型如圖4所示.

圖4 有限元網格

在使用邊界面法進行分析的過程中，共劃分6 494個二次單元(包括三角形單元和四邊形單元)，共29 139個計算節點，網格模型如圖5所示.

3.5 求解結果及對比

圖6和圖7分別為ABAQUS與BFM溫度分布的計算結果對比.

圖5 BFM網格

圖6 有限元計算結果

圖7 BFM計算結果

對比上面兩圖，可以看出邊界面法與有限元法分析結果基本相同，溫度最大值均為20.7 ℃，且溫度等值線高度一致.為做更加清晰詳細的對比，我們取如圖8所示的兩個截面上的節點溫度，繪成溫度曲線進行對比．

圖8 截面示意圖

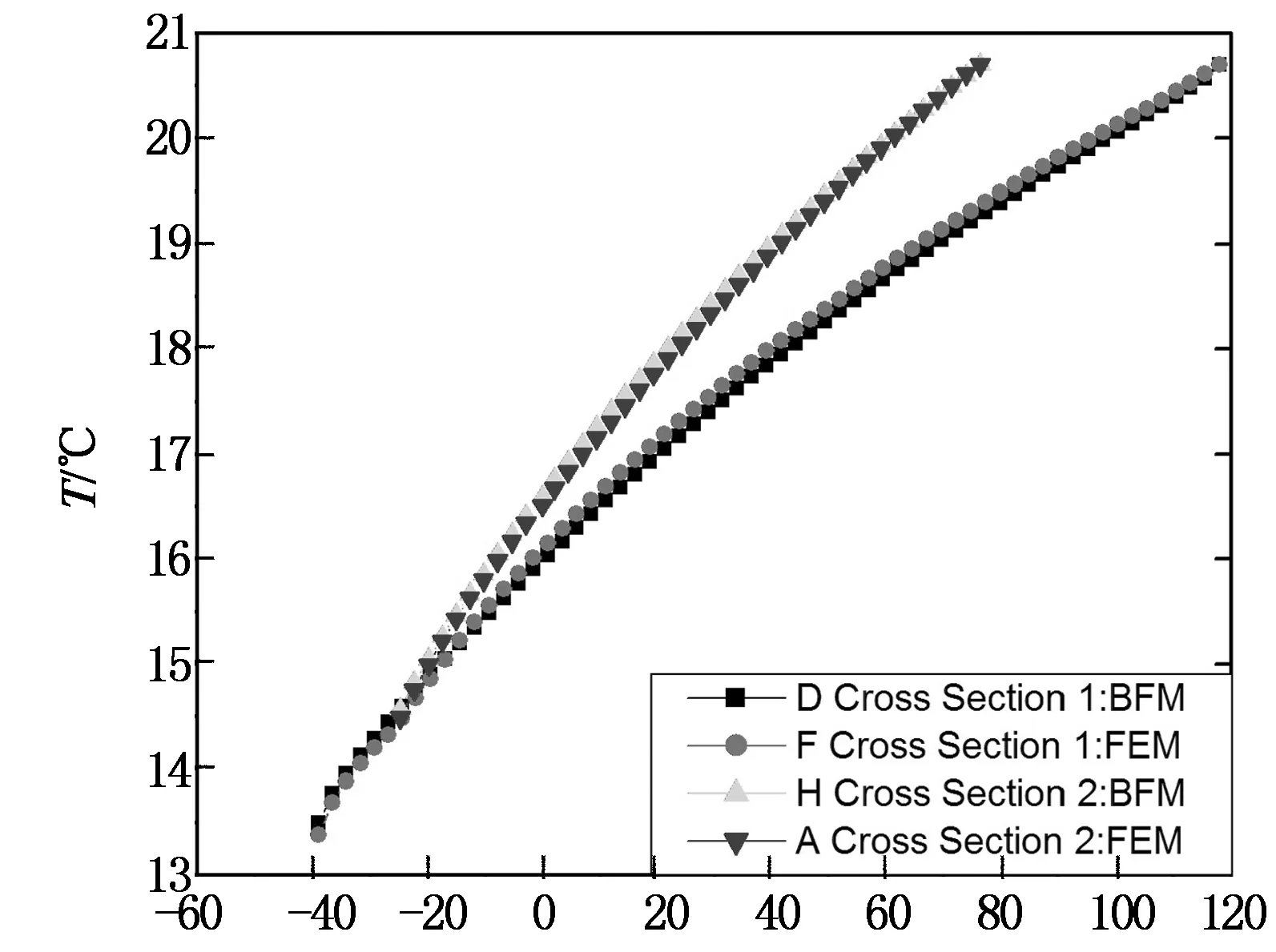
以x軸為橫坐標，繪出上面兩個截面上各個節點的溫度值，組成溫度曲線，如圖9所示．

x

可見，對于有限元法和邊界面法的計算結果，截面1和截面2上的溫度曲線都保持高度一致.上述兩方面的對比可說明邊界面法的計算結果與有限元基本一致.

因此，邊界面法應用于大規模工程結構的穩態熱分析，具有良好的精度.而且，在邊界面法的計算中，計算時長共用了83 s，有限元法用了257 s.并且，由于邊界面法是直接基于幾何模型進行操作，無需定義多個域的裝配以及面間的接觸等，因此邊界面法消耗較少的人力和計算機資源，具有更高的計算效率.

4 結 論

本文用邊界面法解決了含有62個澆筑層的大壩的穩態熱傳導問題.通過和有限元法的對比，證明了計算結果的正確性.說明本文所提出的多域邊界面法可以應用在大規模工程問題中的穩態熱分析中，并且更加便捷，具有更高的效率.

在后續工作中，我們將實現多域邊界面法在瞬態熱傳導問題中的應用，并且考慮通過優化矩陣的組裝方式，來進一步提升計算效率.

[1]ZHANG J M,TANAKA M.Fast HdBNM for large-scale thermal analysis of CNT-reinforced composites[J].Computational Mechanics,2008,41:777-787.

[2]龍述堯.邊界單元法概論[M].北京：中國科學文化出版社,2002.

LONG Shu-yao.The introduction of boundary element method[M].Beijing:China Science and Culture Press,2002.(In Chinese)

[3]HANG J M,YAO Z H,LI H.A hybrid boundary node method[J].International Journal for Numerical Methods in Engineering,2002,53:751-763.

[4]ZHANG J M,YAO Z H,TANAKA M.The meshless regular hybrid boundary node method for 2-D linear elasticity[J].Engineering Analysis with Boundary Elements,2003,27:259-268.

[5]QIN X Y,ZHANG J M,LI G Y,etal.A finite element implementation of the boundary face method for potential problems in three dimensions[J].Engineering Analysis with Boundary Elements,2010,34:934-943.

[6]GU J L,ZHANG J M,LI G Y.Isogeometric analysis in BIE for 3-D potential problem[J].Engineering Analysis with Boundary Elements,2012,36:858-865.

[7]GU J L,ZHANG J M,SHENG X M,etal.B-spline approximation in boundary face method for three dimensional linear elasticity[J].Engineering Analysis with Boundary Elements,2011,35:1159-1167.

[8]GU J L,ZHANG J M,SHENG X M.The boundary face method with variable approximation by b-spline basis function[J].International Journal of Computational Methods,2012,9:9-18.

[9]ZHUANG C,ZHANG J M,QIN X Y,etal.Integration of subdivision method into boundary element analysis[J].International Journal of Computational Methods,2012,9:19-29.

[10]XIE G Z,ZHANG J M,QIN X Y,etal.New variable transformations for evaluating nearly singular integrals in 2D boundary element method[J].Engineering Analysis with Boundary Elements,2011,35:811-817.

[11]張見明，余列祥，劉路平.基于GPU加速的邊界面法正則積分的研究[J].湖南大學學報:自然科學版,2013,40(3):41-45.

ZHANG Jian-ming,YU Lie-xiang,LIU Lu-ping.Research on regular integration in boundary face method based on GPU-acceleration[J].Journal of Hunan University:Natural Sciences,2013,40(3):41-45.(In Chinese)

[12]肖金生,錢耀南,冉一元.柴油機活塞熱負荷的軸對稱分區邊界元分析[J].武漢水運工程學院學報,1986,10(2):69-78.

XIAO Jin-sheng,QIAN Yao-nan,RAN Yi-yuan.Axisymmetric subregion boundary element analysis of thermal loading of the disel engine’s piston[J].Journal of Wuhan University of Water Transportation Engineering,1986,10(2):69-78.(In Chinese)