基于解析模態分解的時變與弱非線性結構密集模態參數識別

王佐才，任偉新，邢云斐

（合肥工業大學 土木與水利工程學院，合肥 230009）

結構健康監測和安全評估已成為國內外眾多學者致力研究的一個重要課題。而其中關鍵問題之一是對結構的參數，特別是時變與非線性系統的時變參數進行有效的識別。因此，近10年來，基于希爾伯特變換在時變和非線性系統識別和損傷檢測領域中得到了廣泛的關注［1－8］。如：Feldman［5］提出的 Hilbert Vibration Decomposition（HVD）方法，并利用該方法對非線性結構的時變參數進行了較為深入的研究。然而，HVD分解對噪聲非常敏感，微小的噪聲對分解的結果也會產生較大的影響，另一方面，如果一個信號具有多個同樣能量量級或者密集頻率的信號分量，HVD也很難將其分解。

為了實現對信號瞬時頻率的識別，黃鍔等［6－8］提出了經驗模態分解（EmpiricalModeDecomposition，EMD）和希爾伯特 －黃變換（Hilbert-HuangTransform，HHT）。EMD能夠將復雜信號分解為有限個本征模函數（IntrinsicModeFunction，IMF），對每一個IMF進行希爾伯特變換和譜分析，可以實現復雜信號的瞬時特征提取，是一種有效的非平穩信號分析工具［9－11］。

雖然HHT在非平穩和非線性信號的特征提取方面取得了廣泛的應用，但在許多實際應用中也遇到了各種困難［12］。例如：HHT無法分離密集的模態響應，特別是具有模態頻率疊混（overlapping）的信號；對于時變的具有模態疊混的結構響應，結構的模態響應也往往存在于多個鄰近的分解信號中，需要進行進一步的重組。為了解決這些難題，國內外的學者也做了相關的研究工作。例如，Chen［13］研究了HHT方法在密集模態結構中模態參數的識別方法，在EMD分解過程中采用間歇檢查（Intermittencycheck）來分離密集模態。Yang［14－15］在進行 EMD分解前，利用帶通濾波器對信號進行濾波預處理，從而把結構的密集模態分離出來。Wang等［16］提出了波組分解的方法，通過把信號的頻率從高頻轉化到低頻，增大相鄰頻率的比值，從而使得EMD有可能把低頻的信號分解出來。程遠勝等［17］提出將HHT與數學規劃方法相結合的方法，用于時變多自由度系統的參數識別。黃天立等［18］提出采用波組信號前處理和正交化經驗模式分解的方法予以改進，并將此方法稱為改進的HHT。然而，對于具有密集模態和時變頻率的信號分解，到目前為止，幾乎還沒有一種有效的方法能夠很好的解決這些問題。另一方面，目前的方法往往簡單地把識別出的響應信號的瞬時頻率等同于結構本身的瞬時頻率，但是，對于時變或者非線性結構系統在環境激勵或者地震荷載作用下的響應信號的瞬時頻率并不等同于結構本身的瞬時頻率，如何利用信號的瞬時頻率來推導時變與非線性結構本身的瞬時頻率也并沒有很好的解決。

Chen等［12］進一步結合希爾伯特變換提出了解析模態分解方法（AnalyticalModeDecompositionAMD）。其本質是利用Hilbert變換把每一具有特定頻率成分的信號解析地分解出來。對于具有多個密集時不變頻率信號分量的復雜信號，AMD通過構造一對具有相同特定頻率的正交函數，并利用這對正交函數與原復雜信號的乘積的Hilbert變換，把任意在頻率小于正交函數頻率的信號解析地分解出來，并最終實現密集模態的參數識別。Chen等［19－20］進一步提到，通過選取一個時變的二分截止頻率代替時不變的截止頻率，AMD可以進一步應用于非平穩信號的分解。

因此，本文為了解決具有密集模態的時變與非線性多自由度體系的時變參數識別問題，首先推導了單自由度與多自由度體系在自由振動和受迫振動下模態響應信號的瞬時頻率與結構本身瞬時頻率之間的關系。本文提出了把解析模式分解方法擴展到時變與非線性結構的模態分解。該方法通過小波變換選取時變的二分截止頻率，對結構的時變模態響應進行分離，從而實現多自由結構時變參數識別。

1 時變與非線性結構系統瞬時頻率識別

1.1 單自由度系統（SDOF）

時變或非線性單自由度系統結構的自由振動運動方程［21］可以簡單的表述為：

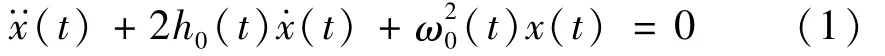
對于非線性結構，非線性恢復力隨時間變化的函數可以轉換成（t）x（t）的形式［21］，（t）是結構瞬時頻率，x（t）是結構位移響應。同樣，非線性阻尼力也可以轉換成2h0（t）x·（t）的形式，h0（t）為快時變瞬時阻尼，x·（t）為速度。

對式（1）進行希爾伯特變換，可得

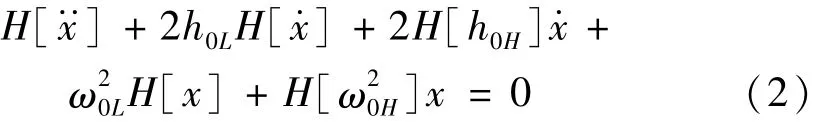
式中：h0L和h0H分別為時變非線性阻尼h0（t）的低通（慢變部分）和高通（快變部分）濾波值；和分別為時變固有頻率（t）的低通（慢變部分）和高通（快變部分）濾波值。

對于單自由度系統的自由振動，位移響應x（t）可以測得，位移的解析信號Z（t）可以表述為

Z（t）＝x（t）＋jH［x（t）］＝A（t）ej∫ω（t）dt（3）式中，A（t）和ω（t）分別是解析信號的瞬時振幅和瞬時頻率。對解析信號求一次和二次導數，可以得到

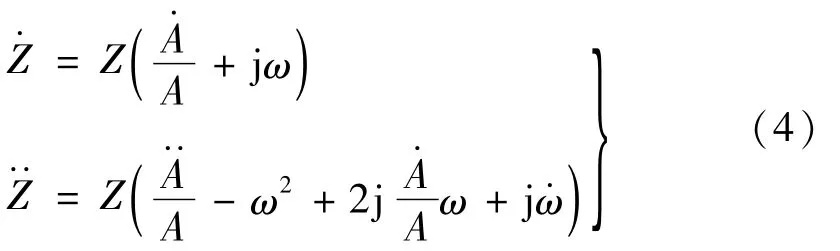
因此，速度和加速度以及它們的希爾伯特變換均可以表述為關于位移的函數

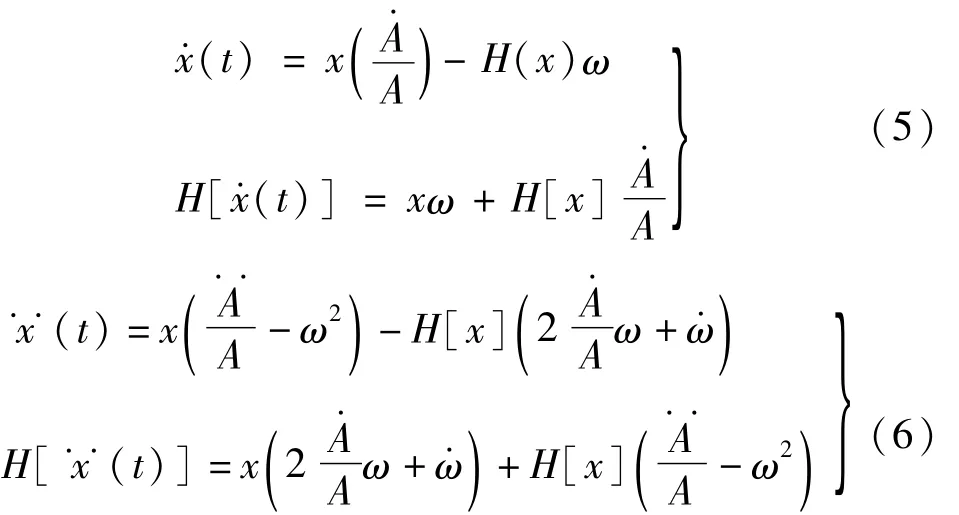
將等式（5）和式（6）代入式（1）和式（2）中，可得

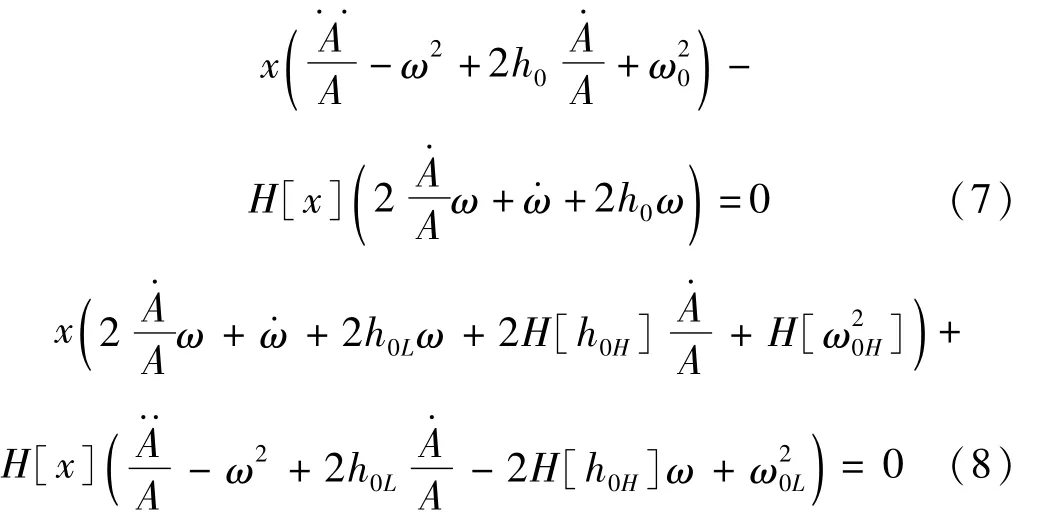
由于任何信號x和它的希爾伯特變換H［x］的相位差為90°，所以它們不可能同時為零。因此，式（7）和式（8）中系數矩陣的行列式必須等于零，從而導出：

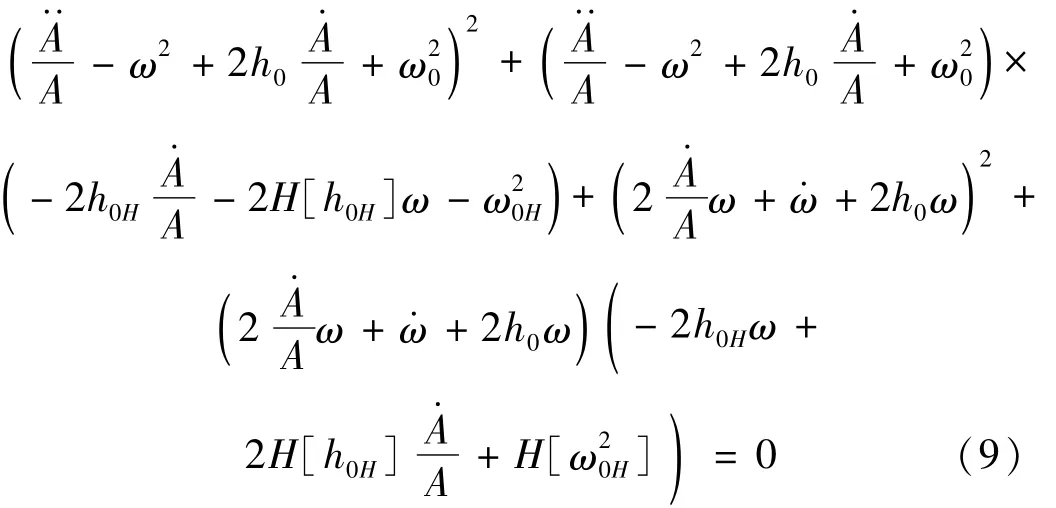
對于單自由度時變或非線性系統的受迫振動，其運動方程可以表述為：

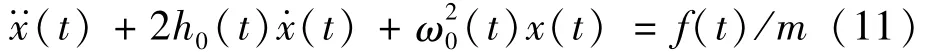
與自由振動類似，如果瞬時阻尼h0（t）和瞬時固有頻率（t）是關于時間的慢時變函數，那么類似的可以推導出瞬時阻尼 h0（t）和固有頻率（t）：

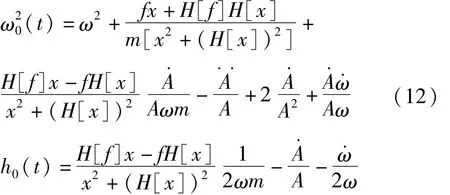
工程實際中，由于響應信號包絡線的導數值都比固有頻率小得多，其影響可以忽略不計，即0。因此，響應信號的瞬時頻率可以寫成：

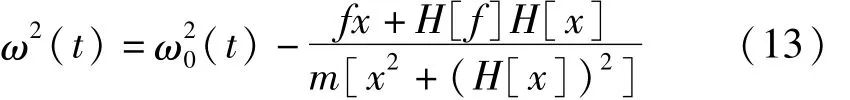
環境激勵或者地震作用f可以假設為具有零均值的時程函數，所以式（13）中的后一部分也是零均值快變的時變函數。如果（t）是弱非線性系統的慢變時變函數，通過AMD方法［12］過濾掉信號瞬時頻率 ω2（t）快變時變的部分，就可以獲得結構系統的固有頻率（t）。

1.2 多自由度系統（MDOF）

對于有n個自由度的時變或弱非線性系統，其運動方程可以表述為

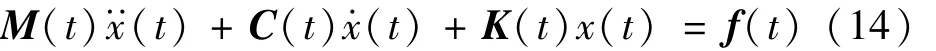
式中：M（t），C（t）和 K（t）分別是時變質量、阻尼和剛度矩陣：f（t）是外荷載。在模態坐標中，式（14）可以轉換為

式中：是第i階模態質量；i是第i階振型向量；（t）是第i階模態響應的固有頻率。模態響應的信號瞬時頻率（t）可以寫成

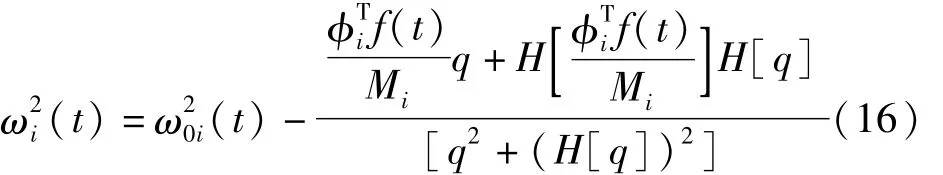
此外，環境激勵或者地震作用f可假設為具有零均值的時程函數，同樣的，式（16）的后一部分是零均值快變的時變函數。通過AMD方法［12］過濾掉模態響應qi（t）的瞬時頻率（t）快變時變的部分，就可以獲得結構系統的第i階固有頻率（t）。

對于多自由度體系，所測得的第I個自由度的位移xl（t）為模態響應 qi（t）函數

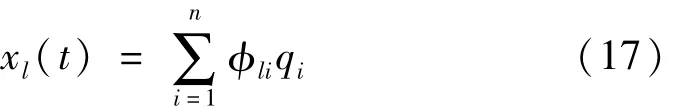
式中：li為第I個自由度的第i階振型向量。因此，從xl（t）中分解而得的第i階模態響應x（i）l（t）可以寫成：

對于有n個自由度的時變或弱非線性系統，li為慢變時變函數且未知，因此，無法獲得第i階模態響應qi（t），而第 i階響應（t）＝liqi則可以通過下文將要介紹的AMD分解方法獲得，其相應的解析信號可表示為

從式（19）可以看出，分離出來的模態響應信號（t）的瞬時頻率等于模態響應qi（t）的瞬時頻率。因此，過濾掉AMD分解得到模態響應（t）的瞬時頻率的快變時變的部分，就可以獲得結構系統的第i階固有頻率（t）。

2 基于AMD方法的時變非線性結構響應信號分解

Chen等［12］首先提出了具有密集模態的時不變信號的解析模式分解定理，并給出了相應的證明。解析模式分解可以描述如下：

對于任意由n個信號分量（t）（i＝1，2，…，n）組成的原信號x（t），如果它的每一分量的頻率 ω1，ω2，…，ωn（ωi＞0；i＝1，2，…，n）滿足：（｜ω1｜＜ωb1），（ωb1＜｜ω2｜＜ωb2），…，（ωb（n－2）＜｜ωn－1｜＜ωb（n－1）和（ωb（n－1）＜｜ωn｜），其中，ωbi∈（ωi，ωi＋1）（i＝1，2，…，n－1）為n－1個二分截止頻率，那么它的每一信號分量可以解析地給出：

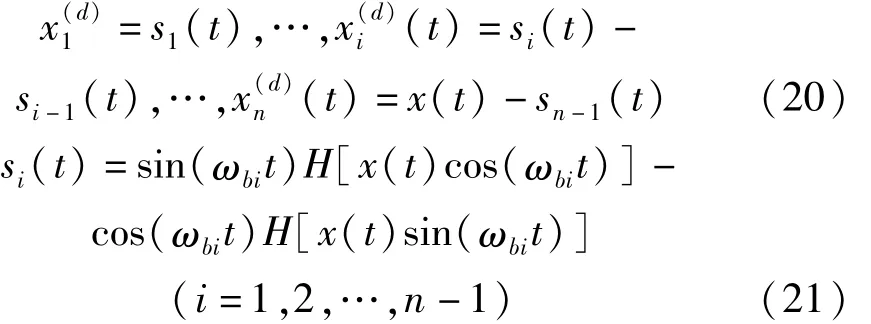
式中，H［·］表示希爾伯特變換運算。

對于具有時變頻率的非平穩信號，本文將解析模式分解定理拓展成如下：

對于任意由n個信號分量（t）（i＝1，2，…，n）組成的原信號x（t），如果它的每一分量的時變頻率ω1（t），ω2（t），…，ωn（t）滿足：｜ω1（t）｜＜ωb1（t），ωb1（t）＜｜ω2（t）｜＜ωb2（t），…，ωb（n－2）（t）＜｜ωn－1（t）｜＜ωb（n－1）（t），和 ωb（n－1）（t）＜｜ωn（t）｜。其中，ωbi（t）∈（ωi（t），ωi＋1（t））（i＝1，2，…，n－1）是選取的時變截止頻率。那么它的每一信號分量可以解析地給出：

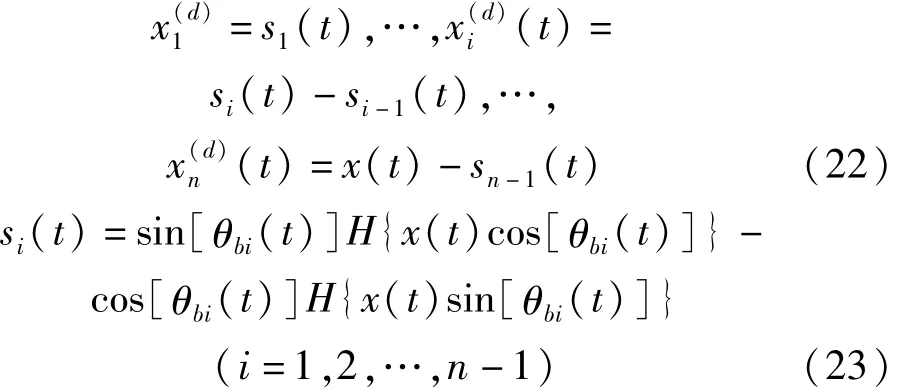
式中：dτ為時變截止頻率的積分，即相位角。

根據上述AMD分解的表述，可以設計如圖1所示的自適應低通濾波器。AMD的本質是利用Hilbert變換把每一具有特定頻率成分的信號解析的分解出來。對于多個時變密集頻率信號疊加的復雜信號，AMD定理通過構造一對具有相同特定時變頻率的正交函數，并利用這對時變正交函數與原復雜信號的乘積的Hilbert變換，把任意在頻率時間平面內低于正交函數時變頻率的信號解析地分解出來。

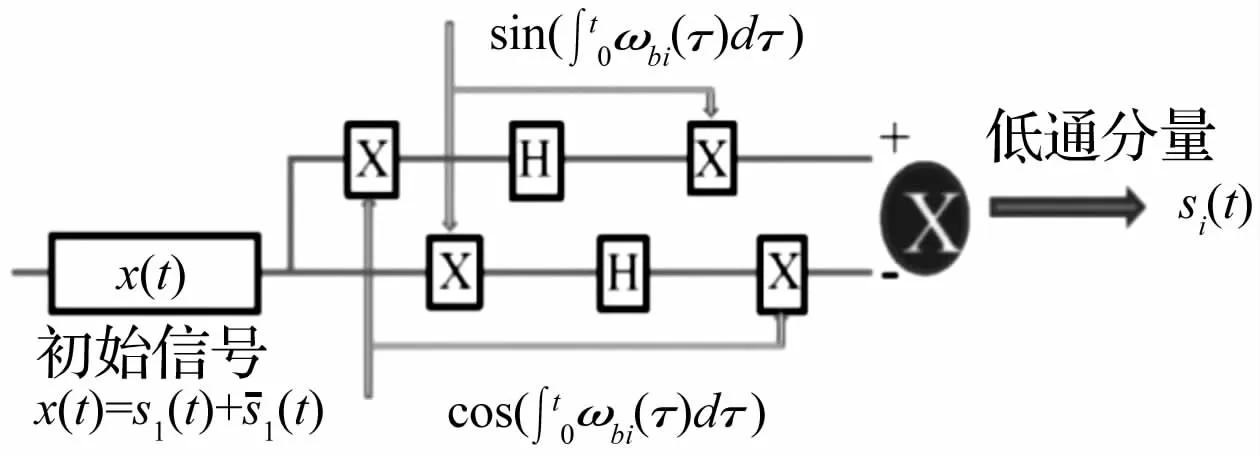
圖1 基于AMD分解的時頻低通濾波器框圖Fig．1 Block diagram of a time-frequency lowpass filter with AMD method

3 自由振動下時變與非線性系統模態參數識別

3.1 自由振動下杜芬系統的瞬時頻率識別

本文首先用硬化彈簧和線性阻尼組成的杜芬系統進行數值模擬，其杜芬方程［21］為

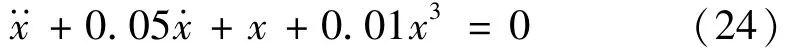
系統初始位移為10 cm，初始速度為0的自由振動信號可由四階龍格庫塔法計算獲得。本算例取時間間隔為0．1 s，其計算得到的自由振動響應和傅里葉譜如圖2所示。

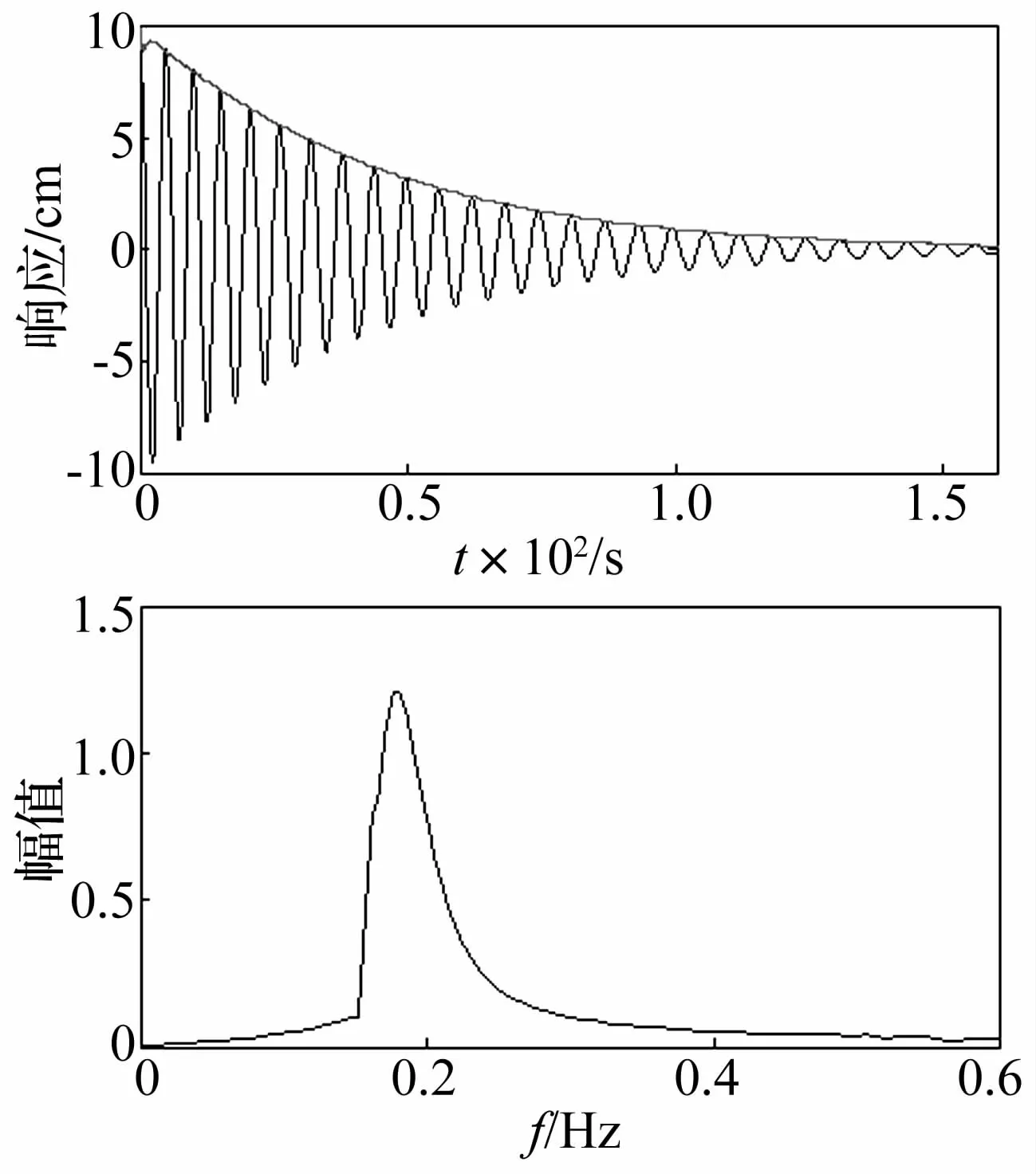
圖2 非線性杜芬系統的自由振動響應和傅里葉譜Fig．2 Free response and its Fourier spectrum of nonlinear Duffing system

對于單自由的體系，通過AMD方法過濾掉信號瞬時頻率的快變時變的部分，就可以獲得結構系統的固有頻率。響應信號的瞬時頻率，阻尼系數以及利用本文方法識別出來的結構瞬時頻率、阻尼如圖3所示。從圖3中可以看出，在振幅較大的時間范圍內，結構非線性硬化程度比較大，結構的瞬時頻率也比較大。自由振動開始時，瞬時頻率迅速下降，最后逐漸趨于相應的線性系統的頻率值（0．16 Hz）。因此，響應信號的瞬時頻率的慢變部分可以準確地反映弱非線性系統的頻率變化。響應信號的瞬時阻尼系數的慢變部分為水平直線（0．025），說明識別出來的阻尼系數為常數0．025，這與杜芬系統的阻尼系數也是一致的。

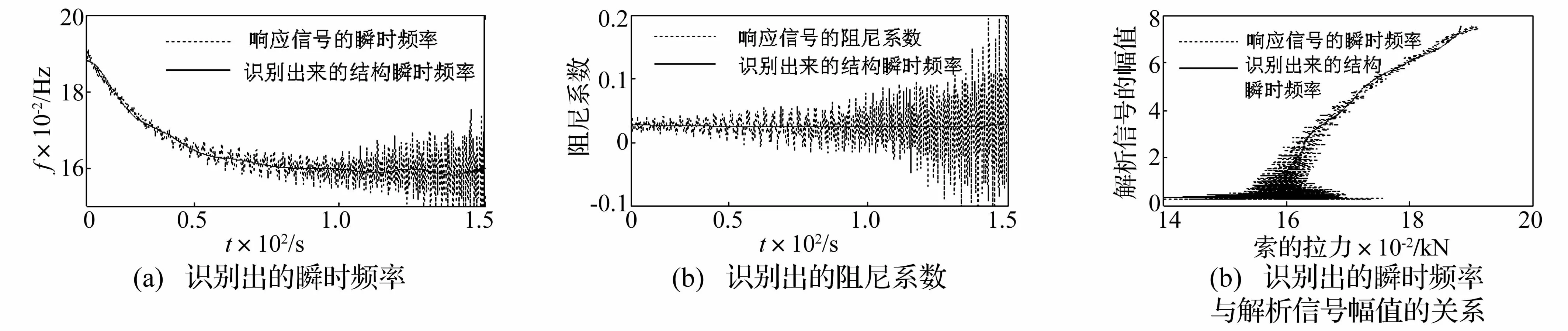
圖3 識別出的瞬時頻率和阻尼系數Fig．3 Identified instantaneous frequency and damping coefficient

3.2 自由振動下索的時變頻率識別試驗

為了驗證本文方法在時變參數識別上的有效性，本文利用文獻［22］的一時變拉索試驗數據進行了驗證。試驗索為一根75的鋼絞線，一端用反力架錨固，另一端固定在MTS加載系統上。兩錨固點間的索長為4．55 m。將加速度傳感器豎向安裝在索的中部，其采樣頻率600 Hz，試驗裝置如圖4所示。拉索由錘子敲擊產生自由振動，本文分別對拉力線性變化和正弦變化兩種情況的時變頻率進行了識別。

圖4 拉索試驗裝置Fig．4 Cable test setup

拉索拉力與索的頻率關系可以通過固定索的拉力，測得索的自由振動響應，并利用峰值法識別出結構在固定拉力下的固有頻率，并把固定拉力下測得的索的固有頻率作為準確值。索的拉力與固有頻率的關系如圖5所示。

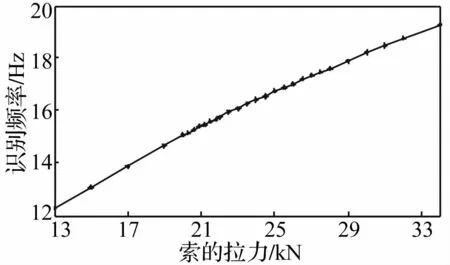
圖5 同定值拉力作用下識別出的一階固有頻率Fig．5 Identified first natural frequency with fixed tension forces

3．2．1 拉力線性變化時索的瞬時頻率識別

試驗時索的拉力從20 kN開始以1．67kN／s的速率線性增加，索力變化過程中同時采集索的沖擊加速度響應，共采集6 s，響應信號如圖6所示。由于用錘子產生自由振動的方式無避免噪聲效應的產生，如果這個噪聲激勵是零均值的，那么所測模態響應中慢變時變部分的瞬時頻率可以看作是索的時變頻率。因此，本文選用二分截止頻率為20 Hz，利用AMD把第一階模態響應分解出來，識別出的響應信號的瞬時頻率和結構的瞬時頻率如圖7所示。從圖中可以看出，測試獲得模態響應信號中的瞬時頻率等于系統的慢變時變頻率加上環境振動的零均值快變的時變頻率。因而模態響應信號中的瞬時頻率的慢變時變頻率部分可以有效地識別出索的時變頻率。

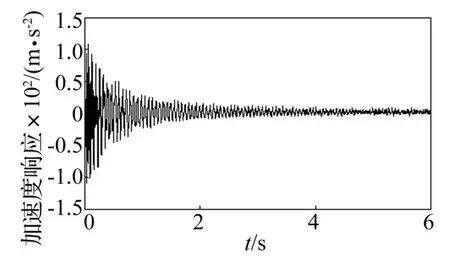
圖6 拉力線性變化時測得索中點處的自由響應Fig．6 Measured free response at middle of cable with linear varying tension force

圖7 拉力線性變化時識別出的瞬時頻率Fig．7 Identified instantaneous frequency with linear varying tension force

圖8 拉力正弦變化時測得索中點處的自由響應Fig．8 Measured free response at middle of cable with sinusoidal tension force

3．2．2 拉力正弦變化時索的瞬時頻率識別

此試驗中，拉力按的方式隨時間正弦變化。同樣，索力變化過程中同時采集索的沖擊加速度響應，共采集6 s。響應信號如圖8所示。通過本文方法識別出的瞬時頻率如圖9所示，從圖中可以看出，模態響應瞬時頻率慢時變的部分與系統瞬時頻率是較為吻合的，可以有效的識別出索的時變頻率。

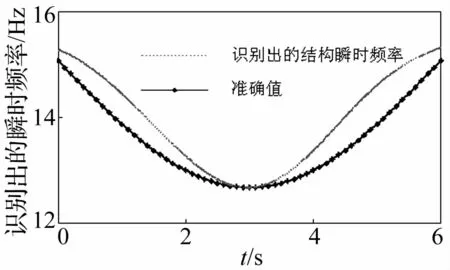
圖9 拉力正弦變化時識別出的瞬時頻率Fig．9 Identified instantaneous frequency with sinusoidal tension force

4 受迫振動下具有密集模態的時變系統參數識別

對一具有密集模態的時變兩層框架系統（圖10）進行數值模擬。下層和上層的集中質量分別為m1＝2．63×105kg和 m2＝1．75×103kg，結構的第一和第二階阻尼比為2%。結構的第一階和第二階固有時變頻率為。對應的結構下層和上層剛度系數為：

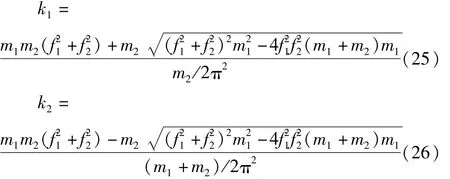
分別對結構在1940 El Centro地震激勵下和具有零均值和0．1 g（g為重力加速度）方差的高斯白噪聲激勵下的響應進行數值模擬，并把第一層模擬的位移響應x1作為實測的時程響應。為了利用AMD對模態響應進行分離，首先選用中心頻率為5 Hz，帶寬為8的復Morlet小波函數，對模擬的信號進行小波變換，獲得小波量圖，并粗略利用模最大的方法提取瞬時頻率脊線（如圖11），從而通過取小波脊線的平均值作為AMD分解的時變截止頻率。利用AMD分解獲得每一階的模態響應如圖12所示。利用本文方法識別的模態響應信號的瞬時頻率和結構瞬時頻率如圖13所示。

該方法首先利用小波變換近似將密集模態的時變頻率脊線提取出來，再根據近似的時變脊線選擇每一信號分量的時變截止頻率，利用AMD分解實現每一信號的分離，而不再需要對信號進行重建。這樣的優點是，根據Heisenberg-Gabor不確定性定理，小波分析不能同時在時域與頻域內達到較高的精度［23］，那么對具有密集模態的時變響應，不僅需要較高的頻率精度，實現模態的分離，同時也需要較高的時間精度，從而可以準確地得到信號的瞬時特征。結合AMD分解的優勢，先通過選擇合適的具有較高頻率精度的小波參數，先選擇失去時間精度的瞬時頻率，利用AMD實現每一信號的分離和本文提取的時變參數識別方法，就可以較精確地得到同時具有較高時間與頻率精度的瞬時頻率。

從圖11中也可以看出，簡單的通過模擬最大提取的小波脊線并不能有效的識別出結構的瞬時頻率。而如圖13所示，結合AMD與本文提出的方法識別出來的結構瞬時頻率與理論值十分吻合，從而有效地識別出了具有密集模態的多自由的瞬時頻率。

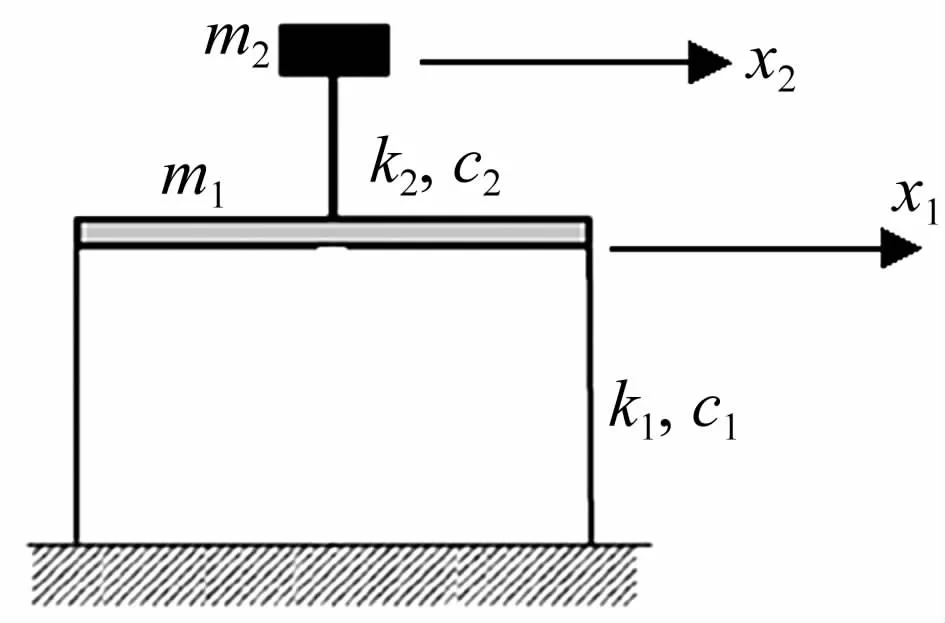
圖10 兩層框架結構Fig．10 Two-story shear building

圖11 基于小波變換的結構瞬時頻率參數識別Fig．11 Instantaneous frequencies by wavelet transform method

圖12 AMD分解的模態響應Fig．12 Decomposed modal responses by AMD

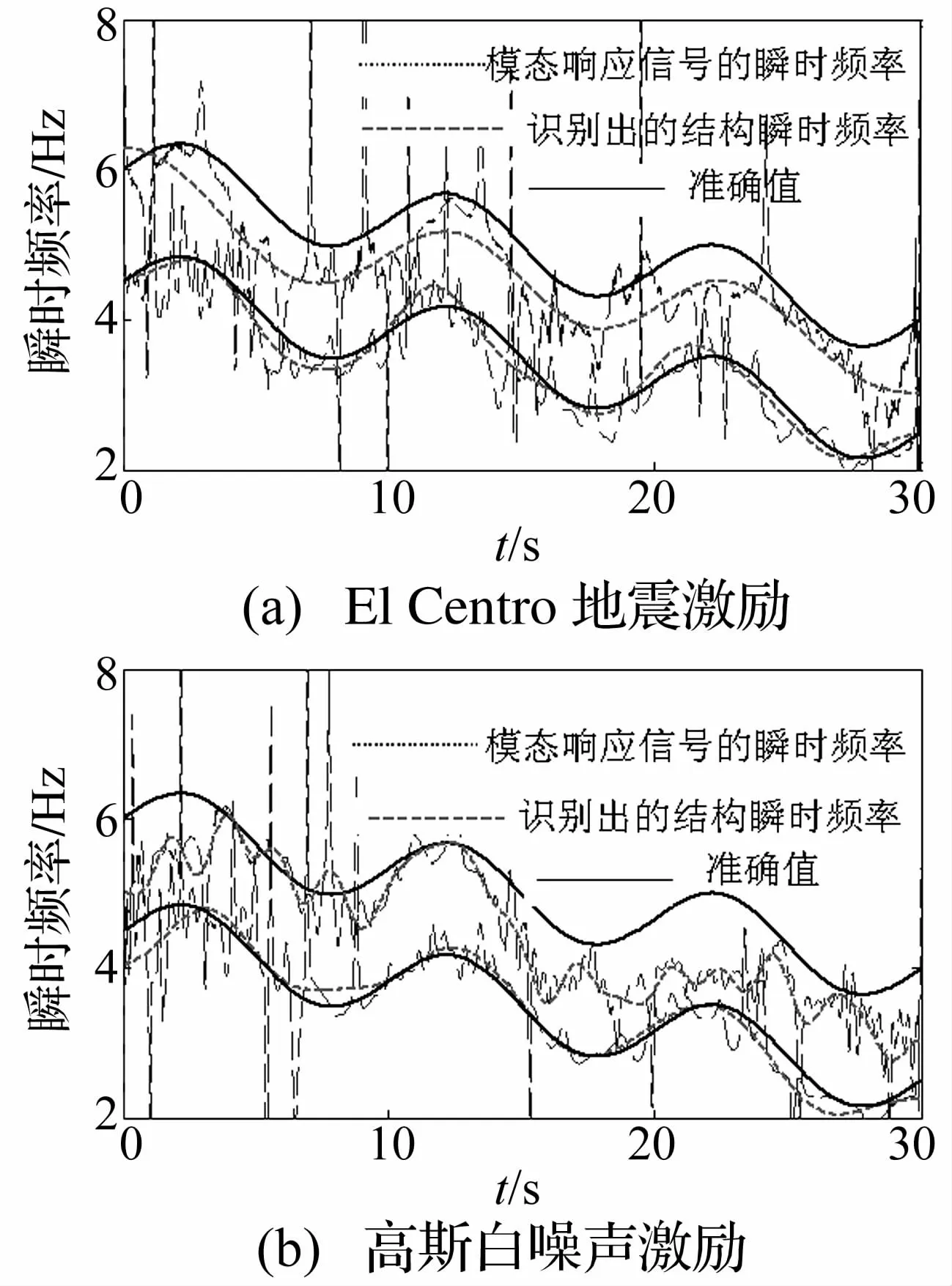
圖13 基于AMD分解方法的瞬時頻率識別Fig．13 Identified instantaneous frequencies by AMD

5 結 論

本文推導了單自由度與多自由度體系在自由振動和受迫振動下模態響應信號的瞬時頻率與結構本身的瞬時頻率的關系。對于具有密集模態的時變與非線性的多自由度體系，通過小波變換選取二分時變截止頻率，并利用本文提出的擴展解析模式分解方法對時變與非線性結構的模態響應進行分解，從而實現對多自由度結構時變參數的識別。通過數值模擬和試驗驗證，可以得到如下結論：

（1）對于時變的線性結構和弱非線性結構，模態響應信號的瞬時頻率緩慢變化的部分與結構系統的瞬時頻率近似相等。因此可以利用模態響應信號中的瞬時頻率的慢變部分有效地識別出結構瞬時頻率。

（2）對于具有密集模態的多自由度結構體系，利用小波變換近似選擇二分時變截止頻率，并利用擴展的解析模式分解方法可以有效地對結構的模態響應信號進行分離，從而實現對具有密集模態的多自由度體系瞬時頻率的識別。

（3）數值模擬和試驗結果表明，本文方法對時變線性和非線性系統結構的瞬時模態參數識別具有較高的時間和頻率精度。

［1］Liu B，Riemenschneider S，Xu Y．Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum［J］．Mechanical Systems and Signal Processing，2006，20（3）：718－734．

［2］Chen H G，Yan Y J，Jiang J S．Vibration-based damaged detection in composite wingbox structures by HHT［J］．Mechanical Systems and Signal Processing，2007，21（1）：307－321．

［3］Feldman M． Non-linear system vibration analysis using Hilbert transform-I：free vibration analysis method［J］．Mechanical Systems and Signal Processing，1994，8（2）：119－127．

［4］Feldman M．Non-linear free-vibration identification via the Hilbert transform［J］．Journal of Sound and Vibration，1997，208（3）：475－489．

［5］Feldman M． Time-varying vibration decomposition and analysis based on the Hilbert transform［J］．Journal of Sound and Vibration，2006，295（3－5）：518－530．

［6］Huang N E，Shen Z，Long S R．A new view of nonlinear water waves：the Hilbert spectrum［J］．Annual Review of Fluid Mechanics，1999，31：417－457．

［7］Huang N E，Shen Z，Long S R，et al．The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis［C］．Proceedings of the Royal Society of London-Series A，1998，454：903－995．

［8］Huang N E，Wu M C，Long S，et al．Confidence limit for the empirical mode decomposition and Hilbert spectral analysis［C］．Proceeding of the Royal Society of London，Series A，2003，459：2317－2345．

［9］羅奇峰，石春香．Hilbert-Huang變換理論及其計算中的問題 ［J］．同濟大學學報（自然科學版），2003，31（6）：637－640．LUO Qi-feng，SHI Chun-xiang．Hilbert transform and several problems in its calculation method［J］．Journal of Tongji University，2003，31（6）：637－640．

［10］陳雋，徐幼麟．HHT方法在結構模態參數識別中的應用［J］．振動工程學報，2003，16（3）：383－388．CHEN Jun，XU You-lin．Application of HHT for modal parameter identification to civil structures［J］．Journal of Vibration Engineering，2003，16（3）：383－388．

［11］黃天立，樓夢麟．基于HHT的非線性結構系統識別研究［J］．地震工程與工程振動，2006，26（3）：80－83．HUANG Tian-li，LOU Meng-lin．System Identification of nonlinear structures based on HHT［J］． Earthquake Engineering and Engieering Vibration，26（3）：80－83．

［12］Chen G D，Wang Z C．A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components［J］．Mechanical Systems and Signal Processing，2012，28：258－279．

［13］ Chen J，Xu Y L．Identification of modal damping ratios of structures with closely spaced modal frequencies［J］．Structural Engineering and Mechanics，2002，14（4）：417－434．

［14］Yang J N，Lei Y，Pan S，et al．System identification of linear structures based on Hilbert-Huang spectral analysis，part I：normal modes［J］．Earthquake Engineering and Structural Dynamics，2003，32（9）：1443－1467．

［15］Yang JN，Lei Y，Pan S，et al．System identification of linear structures based on Hilbert-Huang spectral analysis，part II：complex modes［J］．Earthquake Engineering and Structural Dynamics，2003，32（10）：1533－1554．

［16］Wang W．Decomposition of wave groups with EMD method in The Hilbert Transform in Engineering［M］．Taylor＆Francis Group，LLC，FL，U．S．A．2005，267－280．

［17］程遠勝，熊飛，劉均．基于HHT方法的時變多自由度系統的參數識別［J］．華中科技大學學報（自然科學版），2007，35（5）：41－43．CHENG Yuan-sheng，XIONG Fei，LIU Jun．Identifying the parameters of multi-freedom degree systems with time varying using Hilbert-Huang transform ［J］．Journal of Huazhong University of Science and Technology，2007，35（5）：41－43．

［18］黃天立，邱發強，樓夢麟．基于改進HHT方法的密集模態結構參數識別［J］．中南大學學報（自然科學版），2011，42（7）：2054－2062．HUANG Tian-li，QIU Fa-qiang，LOU Meng-lin．Application of an improved HHT method for modal parameters identification of structures with closely spaced modes［J］．Journal of Central South University，2011，42（7）：2054－2062．

［19］Chen GD，Wang Z C．Response to the letter to editor by Dr．M．Feldman entitled a signal decomposition or lowpass filtering with Hilbert transform［J］．Mechanical Systems and Signal Processing，2011，25（8）：3204．

［20］Feldman M．A signal decomposition or lowpass filtering with Hilbert transform［J］． Mechanical Systems and Signal Processing，2011，25（8）：3205－3208．

［21］Feldman M．Hilbert transform applications in mechanical vibration［M］．Wiley，2011：292．

［22］王超，任偉新，黃天立．基于復小波變換的結構瞬時頻率識別［J］．振動工程學報，2009，22（5）：492－496．WANG Chao，REN Wei-xin，HUANG Tian-li．Instantaneous frequency identification of a structure based on complex wavelet transform ［J］．Journal of Vibration Engineering，2009，22（5）：492－496．

［23］Flandrin P． Time-frequency／time-scale analysis［M］．Academic press，San Diego，CA，1999．