推進器系統激勵下水下航行器結構中功率流分布特性及優化設計研究

劉貴杰，閆 茹，姚永凱，李蒙蒙，張 禹

（中國海洋大學 工程學院，青島 266100）

自治水下機器人（Autonomous underwater vehicle，AUV）是研究海洋、獲取海洋中豐富資源的重要手段，隨著對海洋全面開發和國際安全防御的需求，在水下執行工作的航行器即將面臨更為苛刻的工作要求［1－2］，比如作業時間增長、工作環境更為惡劣，為確保AUV能夠在復雜環境條件下安全工作，有必要針對其結構疲勞進行研究，利用功率流傳播特性來探究水下航行器結構疲勞裂紋是很有價值的。韓旭等［3］基于諾頓等效系統方法計算功率流。該方法的不同之處在于它是針對多維振動的傳遞特性進行的研究，通過計算各個子系統節點的力和速度大小得到振動功率流。并通過對各個維度傳遞的振動功率流進行分析，發現影響振動傳遞的主要因素是系統結構的柔性，王錦麗等［4］研究了加載頻率對懸臂梁振動疲勞特性的影響。用實驗的方法測量了應力周期變化規律，最后結合懸臂梁的疲勞損傷量，在控制初始應力不變的情況下研究了頻率與疲勞損傷裂紋之間的關系。

在海洋環境下長期工作的水下航行器，不斷受到來自海流、海浪波動的隨機變幅疲勞載荷作用，為實現各自由度運動，還需考慮源于推進器的激勵，所以其工作環境相當復雜，至今沒有人專門研究過。本文以小型魚雷式AUV作為研究對象，深入展開討論了在推進器系統激勵下水下機器人中功率流傳播特性。并利用FEM優化平臺結合振動功率流思想提出AUV外形優化方案，根據該優化方案求解了殼體尺寸最優解，以蛛網圖的形式對比了高低頻處結構聲強振動幅值與波動范圍，印證了此優化思想。

1 基于有限元的功率流計算

1.1 小型AUV物理模型

本文采用小型模塊化AUV三段式回轉體Myring外形系列。其中進流段長度為325 mm，去流段長690 mm，采用 B－spline樣條曲線。中間平行段長度為1 470 mm，直徑為 300 mm。其殼體脊線圖如圖 1所示。

圖1 小型模塊化魚雷式AUV殼體脊線圖及特征點分布Fig．1 Ridge image and distribution of feature points of small modular torpedo AUV

1.2 有限元中振動功率流定義［5］

時域中的瞬時結構聲量可以定義為：

式中：σkl（t），vi（t）分別表示 t時刻在 l方向上的響應應力和速度分量。

對于穩態振動，頻域中的復雜殼體結構聲強表示如下：

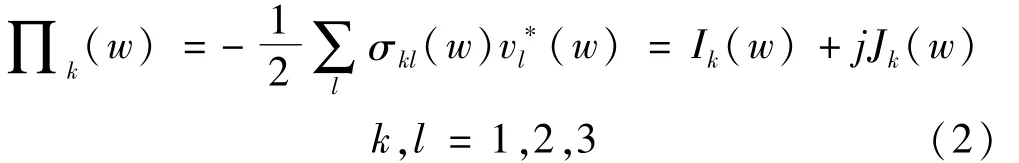
式中 σkl（w）表示應力 σkl（t）的傅里葉變換；v*l（w）表示速度vi（t）傅里葉變換的復共軛；Ik（w）表示衍生振動場相關聯的振動強度；Jk（w）表示振動場中混響的反應強度。

假定薄膜結構在厚度或者橫截面上的應力分布是線性的。應力和位移場是由應力合成，轉化和中面角位移進行定義。結構強度可以用殼或板的單位寬度凈能量流表示。功率流分布在結構中面的切面上，中面上任意一點的位移都可以用平移和角位移表示，單位薄板結構聲強的兩個分量分別寫為：

式中 Nx、Ny、Nxy、Nyx代表面內薄膜力，Nx、Ny代表面內軸向方向力，Nxy＝Nyx代表面內剪力；Qx、Qy代表橫向剪力；Mx、My代表彎矩；Mxy、Myx代表扭矩；u*、v*、w*代表x、y、z三方向平動位移復數共軛x、y、z三方向轉角復數共軛。

對受集中載荷的作用的小型模塊化魚雷式AUV模型，利用阻抗理論可以導出系統中受激勵節點的輸入功率，激勵力的復數幅值Fin（w），系統激勵點速度Vr（w），結構時間平均輸入功率

經過阻尼能量耗散或傳遞臨近結構后輸出功率流：

式中Fs（w）表示阻尼力復數幅值，（w）表示輸出點處速度共軛復數。

2 基于FEM的水下機器人傳播功率流特征研究

2.1 模型特征點振動傳播功率流

小型模塊化魚雷式AUV尾部十字螺旋槳推進器屬于穩態振動激勵，頻率響應分析是計算結構在穩態振動激勵下的響應方法，在該分析中，激勵載荷在頻域中是顯式定義的，對于外載頻率加載都是已知的，穩態振動響應與載荷以相同的頻率出現，由于系統的阻尼影響，響應在時間上出現位移，該位移又稱為相位位移，因此載荷峰值與響應峰值不是同時出現的。計算結果數據包括節點位移、速度、加速度、單元力、單元應力，這些數據恰好是利用有限元進行分析振動功率流的變量因子。本文對小型AUV進行結構動力學分析，模型長度約2．5 m，外徑約0．3 m，彈性模量 E＝2．07×1011Pa，泊松比 μ＝0．3，結構密度 ρ＝7 800 kg／m3，殼壁厚度6 mm。由于模型外形比較復雜，而進行振動功率流分析必須清楚的掌握模型中每個節點每個單元的動力響應量，所以處理Quad4單元數據比Tri3數據更簡捷，計算數據更精確，也方便做功率流后處理，為此采用nastran進行模態頻率響應分析，網格采用QUAD四單元節點，單元數960，節點數1 214，結果如下表1所示。

通過結果可以看到前六階模態是剛體模態，在此不作參考，為此頻域范圍不妨設為［0，1 000 Hz］。計算得螺旋槳推進器所產生的推力大小為F推＝F阻＝FDf＋FDp＝27．7 N，因此本文選取的推力大小為28N。推力計算方法詳見文獻［6］。

圖2所示為振動功率流在小型模塊化魚雷式AUV模型中傳播特性曲線。

表1 模態分析結果Tab．1 Modal analysis results

圖2 利用有限元計算激振力節點功率流Fig．2 Calculation of centrifugal force input node power flow using finite element

圖3 模擬公式數值計算的功率流變化曲線Fig．3 Input power flow curve by numerical simulation

圖4 形體中結構聲強變化曲線Fig．4 Structural intensity curve in body

可以看到，在以上求解頻域范圍內，利用解析法計算的振動功率流與有限元分析得到的功率流變化趨勢基本吻合，這表明了有限元模型建立的有效性，進而可以使用有限元分析方法直觀實現結構聲強的等值線可視化以及流線型殼體優化設計，使研究更為直觀可靠。根據變化趨勢，可以說明模型中存在截止頻率，在截止頻率之內是沒有能量輸入的，振動功率流變化曲線中主要出現三個峰值，理論上應該是對應的不同圓柱殼周向模態數，結合建立的有限元模型，觀察形體中的結構聲強的變化。進行功率流后處理得到形體中結構聲強變化曲線（頭部、中部、尾部）如圖5。

圖5 小型模塊化魚雷式形體能量傳播曲線Fig．5 Energy propagation along small modular torpedo body

考慮基于虛擬質量法的前十五階固有頻率值，本文所選擇的頻域范圍在200 Hz到800 Hz之間，以單元坐標系X、Y軸為基礎數值計算結構聲強Ix、Iy，最后在長度 2．5 m范圍內，分別取 300 Hz、400 Hz、500 Hz、800 Hz處說明形體中能量流動情況。我們可以看到，在某頻值點內，水下機器人結構中是沒有能量傳輸的，激勵力頻率高于該頻值點后才會有能量的輸入，也就是針對不同的結構會出現截止頻率，外載頻率要高于該截止頻率，才會有能量流傳播振動的產生。不同激振頻率下結構聲強曲線都會對應相應的峰值，而峰值出現處都位于殼體三段的交接位置，外載激振力的頻率越高，對應的峰值越明顯。根據X、Y方向上的結構聲強曲線，對振動貢獻率最大的部分是Y軸方向，也就是殼體前后伸縮振動，由此也可以看到拉伸波在傳播過程中所占比例最大。

2.2 結構聲強等值線可視化

可視化技術集成人機交互、計算機輔助設計、計算機圖形學等多方面領域，與相應的工程計算數據結果相結合，通過曲線關系圖說明數據之間的相互關系以及遞變規律。等值線可視化技術的處理過程有以下幾點，首先對科學運算產生的數據進行處理，使數據格式標準統一，其次根據數據對應的函數變量進行一一對應，最后編寫相應的程序得到模型結構中等值線的分布情況［7－8］。

本節結合patran后處理功能，并利用相關PCL語言，根據結構聲強殼單元表達式，將模型表面節點相等的結構聲強數值以相等數值的連線來表達結構上能量等值線圖，根據等值線分布圖來表現能量起伏波動情況，能量等值線形式以光滑連續曲線表達，首尾封閉，互不相交。以下使用能量等值線技術，從可視化角度出發著重表達模型中能量分布和波動問題，結合PCL語言，能量總值取對模型表面的能量計算數值取整，分別在400 Hz、800 Hz頻值點處繪制等值線圖，如下所示

圖6 400 Hz模型表面能量分布等值線Fig．6 Energy distribution contour on model surface when f＝400 Hz

圖7 800 Hz模型表面能量分布等值線Fig．7 Energy distribution contour on model surface when f＝800 Hz

根據上述的能量等值線分布圖形，發現隨著激振力頻率增加，能量等值線密度在表面越來越大，圖中等值線最高點隨頻值不同也有不同變化，400 Hz處模型能量等值線密度較為疏松，最高值集中于頭部，而且該處能量波動也較為強烈，雖然本文沒有考慮流體因素的影響，但水下機器人在水中航行時，頭部也是受粘壓阻力最為明顯的位置，對殼體橫剖面而言，能量大小差異不大，等值線以圓環類分布為主，在高頻段800 Hz處，水下機器人殼體首尾的能量密度明顯增大，變化強烈區域主要集中在殼體中間部位，能量最大值位于頭部與尾部，在波傳動過程中拉伸波與彎曲波同時體現出了自身的作用，相應的等值線存在形式以半環形與弦形為主，綜合以上說明在低中頻階段，模型頭部能量不僅波動大而且數值大，在高頻階段，能量波動位置出現在中間段部位，但最高點位于頭部與尾部，該等值線分布圖與小型模塊化魚雷式AUV形體能量傳播曲線所說明的結果相互吻合。

3 基于功率流的小型AUV流線型殼體優化設計

本文主要以流線型殼體頭尾部關鍵點作為輸入變量，結構聲強計算公式中的單元薄膜力作為輸出變量，通過設定等式及不等式約束條件作為變量的依附關系，實現AUV殼體外形動力響應優化［9－10］，具體優化流程如圖8所示。

對該優化問題的描述如下：

（1）優化設計變量：小型AUV尾部六個特征點到中轉軸的距離p1→p6，頭部三個特征點p7→p9。

（2）約束條件：頻率響應分析單元薄膜力（X、Y、Z三方向軸向力與X、Y、Z三方向剪切力）和結構平均內應力小于初始設計值。

（3）目標：設計目標是使小型AUV殼體單元結構聲強最小，即：

3.1 基于Ansys Design Exploration平臺的優化求解

采用Ansys Deign Exploration平臺進行優化求解，有利于實現功率流性能快速優化，減小單一軟件分析誤差。同時對于多自變量因變量優化設計而言，需要確定每自變量相對因變量的敏感度，敏感度越高，相應設定因變量的優先級別也越高，優化迭代后計算的數據結果參考價值越大。

圖9 變量相關矩陣Fig．9 Variable related matrix

圖10 變量判斷矩陣Fig．10 Variable judgment matrix

圖9根據相關系數計算出變量間相關矩陣方形圖，圖標中數值代表相關系數大小，數值范圍［0，1］．相關系數為1時，表示正相關，相關系數為－1時，表示負相關，正相關時自變量增大隨之因變量增大，負相關時自變量增大隨之因變量減小，對角線處都是原矩陣與自身的相關系數，所以數值都為1，圖10表示變量參數的判斷矩陣，利用判斷矩陣可以判斷出各因素的相對重要性

確定輸入輸出變量相對優先性等級之后，需要進行優化迭代運算，圖11主要展現輸出變量在輸入變量迭代運算后所經歷的數值波動范圍，進而說明目標參數在優化過程中變化情況。

圖11 輸出變量蛛網圖Fig．11 Spider diagram of output variables

3.2 結果分析

尺寸參數最優解數值表格見表2。圖12對比展現了AUV初始設計與優化設計后流線型殼體中應力強度云圖與頻響分析中平均Y軸向單元力變化曲線。

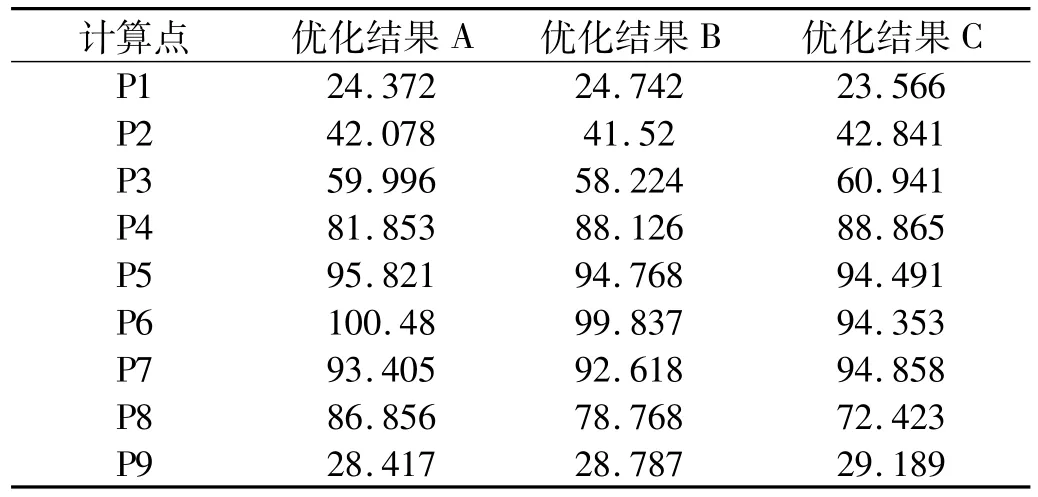
表2 AUV殼體外形尺寸參數優化解Tab．2 Parameter optimization solutions of AUV shell size

圖12 不同殼體模型結果對比圖Fig．12 Comparison result ofdifferent shell model

對比以上數據可以看出優化尺寸A、B對應的應力強度最大值有所降低，殼體應力云圖成對稱性，分布情況較原始云圖更均勻，諧響分析Y軸向平均應力最大振幅變小，優化尺寸C所對應的應力幅值雖然增加，但是明顯減緩了應力集中情況，三組最優解對應的單元應力呈現不同的變化趨勢，考慮最終目標為減緩殼體中振動功率傳播幅值，所以暫不考慮應力集中問題，對比A、B尺寸，選取平均內力較小的A尺寸，繪制節點結構聲強傳播曲線蛛網圖，對比優化前后結構聲強變化情況如圖13。

圖13 結構聲強對比蛛網圖Fig．13 Contrast spider diagram of structural intensity

兩實線處表示優化前各節點結構聲強數值，兩虛線處表示優化后結構聲強數值，結果分別展現400 Hz、800 Hz處的結構聲強變化情況，通過圖13可以看到在高低頻處，優化后的結構聲強在振動幅值與波動區域處均有所降低，而且在高頻區域表現明顯，前后結果數據對比說明了該優化方案的可行性。

4 結 論

（1）完成AUV模型中動力學仿真及數據處理。發現不同激振頻率下結構聲強曲線都會對應相應的峰值，而峰值出現處都位于殼體三段的交接位置，外載激振力的頻率越高，對應的峰值越明顯，并且拉伸波在傳播過程中所占比例最大。

（2）實現了基于振動功率流方法的AUV外形優化。利用結構聲強蛛網圖的形式展現了優化方案的可行性與有效性，同時為AUV外形優化方法提出了一種新的優化思想。

［1］張文瑤，裘達夫，胡曉棠．水下機器人的發展、軍事應用及啟示［J］．中國修船，2006，19（6）：37－39．ZHANG Wen-yao，QIU Da-fu，HU Xiao-tang．The evolution、military and inspiration of underwater vehicle［J］．China Shiprepair，2006，19（6）：37－39．

［2］李曄，常文田，孫玉山，等．自治水下機器人的研發現狀與展望［J］．機器人技術與應用，2006，19（1）：1－7．LI Ye，CHANG Wen-tian，SUN Yu-shan，et al．Present research and development trends of autonomous underwater vehicle［J］．Robot Technique and Application，2006，19（1）：1－7．

［3］韓旭，郭永進，朱平，等．基于諾頓等效系統功率流計算的多維振動傳遞特性研究［J］．振動與沖擊，2007，26（5）：240－246．HAN Xu，GUO Yong-jin，ZHU Ping，et al．Study on multidimensional vibration transmission performance based on vibration power flow calculation with Norton equivalent system［J］．Journal of Vibration and Shock，2007，26（5）：240－246．

［4］王錦麗，李玉龍，胡海濤，等．加載頻率對懸臂梁振動疲勞特性的影響［J］．振動與沖擊，2011，30（6）：243－247．WANG Jin-li，LI Yu-long，HU Hai-tao，et al．Effect of load frequency on vibration fatigue behavior of cantilever beam［J］．Journal of Vibration and Shock，2011，30（6）：243－247．

［5］Li Y J，Lai J C S，Prediction of surface mobility of a finite plate with uniform force excitation by structural intensity［J］．Applied Acoustics，2000，60（3）：371－383．

［6］Liu GJ，Yan R，et al．Analysis and forecast of hydrodynamic simulation for small autonomous underwater vehicle［J］．International Conference on Mechanical and Electronic Engineering，ICMEE，2012：159－164．

［7］胡星，楊光．流線可視化技術研究與進展［J］．計算機應用研究，2008，83（5）：8－12．HU Xing，YANG Guang，et al．Streamline visualization：research and development［J］．Computer Application Research，2008，83（5）：8－12．

［8］任碧寧，魏生民，羅衛平．三維CFD矢量場自適應流線耙并行計算［J］．西安電子科技大學學報，1999，26（5）：646－650．REN Bi-ning，WEI Sheng-min，LUO Wei-ping．Parallelization of an adaptive step particle tracing method on PVM［J］．Journal of XiDian University，1999，26（5）：646－650．

［9］Ruzzene M，Baz A．Active／passive control of sound radiation and power flow in fluid-loaded shells［J］．Thin-Walled Structures，2000，38（1）：17－42．

［10］李海飛，王敏慶，張教超．梁上附加集中質量對梁－板耦合系統功率流特性的影響［J］．振動與沖擊，2012，31（12）：185－188．LI Hai-fei，WANG Min-qing，ZHANG Jiao-chao．Effects of added point masses on power flow features of a mass-loaded beam-plate coupled system［J］．Journal of Vibration and Shock，2012，31（12）：185－188．