基于雙共振的渦街信號檢測方法

鄭 俊，林 敏

（中國計量學院 計量測試工程學院，杭州 310018）

自Benzi等［1］提出隨機共振以來，基于隨機共振的微弱信號檢測技術已經在生物醫學、光學、機械設備故障檢測等領域中獲得了廣泛應用［2－4］。隨機共振是一種非線性現象，在輸入弱周期信號和噪聲的共同作用下，非線性系統的輸出信噪比會隨著噪聲強度的變化而呈現出先增大后減小的非單調變化。目前，在微弱信號檢測與處理中，常規的信號處理方法的目標均集中在如何抑制噪聲上，如相關檢測、時域平均、FFT譜分析等。然而，當噪聲頻率與信號頻率相近或重合時，常規的微弱信號檢測方法便無能為力。與各種抑制噪聲的傳統微弱信號檢測方法相反，隨機共振是利用噪聲來增強系統的輸出信噪比，從而檢測出微弱信號［5－6］。

作為隨機共振走向應用的關鍵，隨機共振的控制也已成為研究熱點。隨機共振控制就是通過各種控制手段有目的地產生或增強隨機共振效果，從而產生某些特定性質的隨機共振輸出響應。研究隨機共振的經典非線性系統模型是雙穩系統［7－9］，雙穩系統具有結構簡單，便于理論分析的優點，只有當雙穩系統、周期信號與噪聲這三者的相關參數存在一定的匹配關系時才能產生隨機共振。但在實際應用中，雙穩系統的結構參數往往固定，輸入信號和噪聲也是給定的，不能通過改變其勢壘高度或閾值以實現隨機共振控制。

將兩個單一雙穩系統通過非線性耦合方法耦合成一個多穩態系統，將其中一個雙穩系統作為參數固定的被控系統，另一雙穩系統當作參數可調的控制系統。與單一雙穩系統相比，耦合雙穩系統具有靈活的隨機共振控制方法［10］。

本文研究了耦合雙穩系統在控制信號作用下的雙共振特性，通過分析控制信號頻率對雙共振的影響，提出了基于雙共振的隨機共振增強方法。將該方法應用于實測的渦街流量信號檢測中，分別選取小流量渦街信號與強背景噪聲干擾下的大流量渦街信號進行檢測，實驗結果表明，控制信號作用后耦合系統存在的雙共振現象能大幅增強隨機共振效果，系統輸出功率譜在特征頻率處的譜值顯著提高，從而能夠準確檢測出強噪聲背景中的渦街信號頻率。

1 耦合雙穩系統雙共振特性

研究隨機共振的經典模型可由如下單一雙穩系統所描述的方程表示

式中，V（x）＝－ax2／2＋bx4／4，為雙穩系統勢函數。a，b為雙穩系統參數。A cos（ω·t）是外界作用到系統中的弱周期信號，其中ω是周期信號的頻率，幅值A1。ξ（t）是滿足〈ξ（t）〉＝0，〈ξ（t）ξ（t′）〉＝2Dδ（t－t′）的高斯白噪聲，其中D為噪聲強度。

引入另一個受周期信號作用的雙穩系統（a0yy3），通過非線性耦合方式，將這兩個單一雙穩系統耦合成一多穩態系統，則控制信號作用下的耦合雙穩系統可由如下方程［11］來表示

式（2）所描述的耦合雙穩系統的靜態勢函數為U（x，y）＝－ax2／2＋bx4／4－a0y4／2＋y4／4＋rx2y2／2，r為耦合系數。將（ax－bx3）當作被控雙穩系統，則（a0y－y3）可作為控制雙穩系統。x（t）為被控系統變量，輸入的外界弱周期信號與噪聲均是作用到被控系統中，因此隨機共振也只在被控系統中產生；y（t）為控制系統變量，控制信號B cos（Ωt＋）作用到控制系統中，控制變量y（t）的改變會直接引起勢函數U（x，y）的變化，進而改變系統勢壘高度，影響被控系統中的隨機共振。

當控制信號幅值B＝0時，考慮僅在耦合作用下時耦合雙穩系統的隨機共振特性。根據隨機共振的線性響應理論［12］，（2）式中被控系統方程的穩態解可表示如下

式中X為系統的響應幅值。將上式代入（2）式中第二個方程，并對方程求解，當t→∞時，可得y（t）穩態解為

進一步簡化［13］有

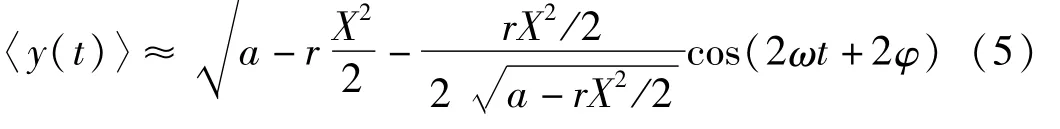
因此，當沒有外加控制信號，僅在耦合作用下時，耦合雙穩系統中的控制系統變量 y（t）將會在2附近做小幅波動，其波動頻率2ω由外界輸入的弱周期信號頻率ω所決定。這是耦合雙穩系統所固有的特性。

當控制信號B≠0時，控制信號作用下的控制系統方程可改寫為

控制系統動態勢函數為

即y（t）在y1或y2附近以頻率Ω作受迫振動。

由于耦合的作用，y（t）是以頻率為2ω做小幅波動。當外加的控制信號 B cos（Ωt＋）的頻率 Ω與 y（t）的固有振動頻率2ω相近或相等時，就會在控制系統中產生共振，引起y（t）大幅波動，進而直接改變耦合系統的勢函數和勢壘高度，從而影響被控系統中的隨機共振。

因此，對于外加控制信號作用下的耦合雙穩系統，改變控制信號頻率將會使耦合雙穩系統中產生雙共振現象，即控制系統中的共振與被控系統中的隨機共振。在耦合作用下，共振可影響與控制隨機共振。

對（2）式中的耦合雙穩系統方程采用四階龍格－庫塔算法對其數值求解，計算時間步長0．02。取被控系統參數a＝1，b＝1，控制系統參數a0＝1，耦合系數r＝0．5。作用到被控系統上的弱周期信號幅值A＝0．1，頻率 ω＝2π·f0＝2π·0．01，噪聲強度 D＝0．15。作用到控制系統中的控制信號的幅值和相位分別取B＝0．06，＝0．4π。通過連續改變控制信號的頻率Ω（Ω＝2π·f），得到圖1所示的被控系統輸出信噪比SNR隨控制信號頻率的變化曲線。由圖可知，隨著f的改變，被控系統輸出的信噪比也隨之改變，當f＝2f0＝0．02 Hz時，系統輸出信噪比具有一個顯著突出的峰值，表明此時隨機共振最強烈。數值仿真與理論分析完全一致，當控制信號頻率2倍于被控系統中弱周期信號頻率時，耦合雙穩系統處于雙共振狀態，控制系統中的共振大幅增強了被控系統中的隨機共振。

圖1 信噪比隨控制信號頻率變化曲線Fig．1 The curve of SNR by changing control signal’s frequency

2 基于雙共振的頻率檢測方法

對于式（2）所確定的耦合雙穩系統，當被控系統在弱周期信號與噪聲的作用下，將會產生隨機共振；給控制系統外加控制信號，改變其頻率大小能使控制系統產生共振。由于耦合的作用，控制系統中的共振能影響并增強被控系統中的隨機共振。提出一種基于雙共振的頻率檢測方法，該方法的檢測原理框圖如圖2所示，具體檢測過程如下：

圖2 雙共振頻率檢測原理框圖Fig．2 The framework of frequency detection based on dual-resonance

（1）將被測信號 A cos（ωt）與噪聲 ξ（t）作為輸入項，輸入至參數固定的被控系統x·＝ax－bx3中，選取合適的耦合系數r與控制系統參數a0，使被控系統在被測信號與噪聲的協同作用下產生隨機共振。

（2）向控制系統y·＝ay－y3中外加頻率可調的控制信號B cos（Ωt＋φ），通過連續調節控制信號頻率Ω，當Ω＝2ω時，外加信號頻率與被控系統固有振動頻率相同，控制系統中將會產生共振。

（3）通過耦合作用r，控制系統中的共振將會影響被控系統的隨機共振，輸出信號x（t）的功率譜圖中特征頻率處的功率譜值增大，隨機共振效果增強，從而檢測出被測信號頻率。

3 實驗結果與分析

渦街流量計是基于卡門渦街原理設計而成的流體振動型流量計，已經在氣體、液體等流量的測量中得到廣泛應用。由于其振動頻率與流速成正比關系，因此準確檢測出流體振動頻率是渦街流量計應用的關鍵。但在現場使用中，各種設備振動尤其管道振動而引起的噪聲干擾會降低測量精度，影響了渦街流量計的測量下限。渦街流量計的輸出信號由兩部分組成：一是因流體流過渦街發生體而產生的正弦周期性渦街信號，二是因各種其他干擾如振動、湍流脈動而產生的噪聲信號。當噪聲干擾較強或在小流量的測量中，常規的渦街信號分析處理方法有時甚至會無法準確獲得渦街頻率，影響了渦街流量計的正常使用。

利用該方法分別對實測的小流量渦街信號與強噪聲干擾下的大流量信號進行檢測。由于待測的渦街信號頻率fd1，不滿足隨機共振線性響應理論所要求的小參數條件，所以先將采集到的原始渦街信號進行變尺度預處理［15］，經耦合系統隨機共振處理后再進行尺度恢復。

3.1 小流量渦街信號檢測

實驗采集流速為4．01 m3／h的小流量渦街信號，采樣頻率fs＝5 000 Hz，采樣點數N＝16 384。圖3為渦街信號的時域波形圖及功率譜圖，由于小流量時渦街頻率很低，背景噪聲相對較大，因此無論時域圖還是功率譜圖中均無明顯的渦街特征信息。設置采樣壓縮比R＝500，經耦合雙穩系統隨機共振處理后再進行尺度恢復。耦合雙穩系統參數 a＝1，b＝1，a0＝0．8，r＝0．6。

圖4（a）為僅有耦合作用時（控制信號B＝0）的耦合雙穩系統輸出功率譜圖。由圖可知，僅在耦合作用下，耦合雙穩系統中已產生隨機共振，但系統輸出功率譜在特征頻率 fr＝0．020 14 Hz處的譜峰值僅為0．010 31，且有他頻率成分的干擾，檢測效果不好。

向控制系統中外加控制信號，其幅值與相位分別取 B＝0．2，＝0．4π。通過連續調節控制信號頻率，當Ω＝2fr時，得到如圖3（b）所示的耦合雙穩系統輸出功率譜圖。可知耦合系統中產生的雙共振大幅增強了被控系統輸出的隨機共振，圖4（b）中系統輸出功率譜圖中在特征頻率fr＝0．020 14 Hz處的譜值進一步增加至0．014 42，幅度增大了近40%。與僅有耦合作用時相比，該譜峰變得更為突出，檢測效果顯著提高。經尺度恢復后得到待測的渦街信號頻率：fd＝fr·R＝10．07 Hz。而 4．01 m3／h時的渦街頻率理論值為 10．30 Hz。檢測結果表明，采用雙共振可準確有效地檢測出待測的小流量渦街信號。

3.2 大流量渦街信號檢測

實驗采集流速為46．28 m3／h的大流量渦街信號，采樣頻率fs＝5 000 Hz，采樣點數N＝10 504。由于噪聲干擾較大，因此無法直接從時域圖及功率譜圖中直接分辨出渦街特征頻率信息，如圖5所示。在經由耦合雙穩系統隨機共振處理前，先進行變尺度預處理，取采樣壓縮比R＝2 000。耦合雙穩系統參數取a＝1，b＝1，a0＝0．9，耦合系數 r＝0．6。

圖6（a）為當控制信號幅值B＝0時，僅在耦合作用下，耦合雙穩系統的輸出功率譜圖。經被控系統隨機共振處理后，圖中在特征頻率fr＝0．059 36 Hz處存在一個并不十分突出的譜峰值，其值為0．156 7，檢測效果受到了其他頻率成分的干擾。

向控制系統中外加單一頻率的控制信號，其參數取B＝0．1，＝0．4π。通過連續調節控制信號頻率，當Ω＝2fr時，得到耦合雙穩系統的輸出功率譜如圖6（b）所示。可知當控制信號作用后，耦合系統中產生的雙共振進一步增強了被控系統的隨機共振，輸出功率譜在特征頻率fr處的譜值由0．156 7增大為0．187 2。與僅有耦合作用時相比，其譜峰值增加了約20%，且fr處的功率譜值變得更為突出，其他頻率成分的干擾也進一步降低，可準確檢測識別出0．059 36 Hz的特征頻率。最后經尺度還原后得到待檢測的渦街頻率如下：fd＝fr·R＝118．72 Hz。而 46．28 m3／h時的渦街頻率理論值為118．60 Hz。實驗結果表明，基于雙共振的隨機共振增強方法可準確檢測出強噪聲背景中的大流量渦街信號，可提高渦街流量計的現場適應性。

圖 3 4．01 m3／h時渦街流量信號時域圖及功率譜圖Fig．3 The time domain waveform and power spectrum of vortex shedding signal under4．01m3／h

圖4 耦合系統輸出功率譜圖Fig．4 The time domain waveform and power spectrum of system output

圖 5 46．28 m3／h時渦街流量信號時域圖及功率譜圖Fig．5 The time domain waveform and power spectrum of vortex shedding signal under46．28m3／h

圖6 耦合系統輸出功率譜圖Fig．6 The time domain waveform and power spectrum of system output

4 結 論

分析了控制信號作用下的耦合雙穩系統的雙共振特性，通過改變控制信號的頻率，耦合雙穩系統的控制系統中會產生共振進而影響被控系統中的隨機共振，并提出了基于雙共振的隨機共振增強與頻率檢測方法。數值仿真分析結果表明改變外加控制信號頻率使控制系統達到共振時，耦合雙穩系統輸出信噪比增大，輸出功率譜在特征頻率處的譜值大幅增加，隨機共振效果顯著增強。將該方法分別應用于實測的小渦街流量信號與強噪聲干擾的大流量渦街信號檢測中，實驗結果表明，通過雙共振能有效增強系統輸出功率譜在特征頻率處的譜值，可準確檢測出渦街信號頻率。該方法可拓寬渦街流量計的測量下限，增強其現場適應性，具有良好的應用前景。

［1］Benzi R，Sutera A，Vulpiani A．The mechanism of stochastic resonance［J］．Physical A，Mathematical and general，1981，14（11）：453－457．

［2］寧麗娟，徐偉．光學雙穩系統中的隨機共振 ［J］．物理學報，2007，56（04）：1944－1948．NING Li-juan，XU Wei． Stochastic resonance in optical bistable system［J］．Acta physica sinica，2007，56（04）：1944－1948．

［3］胡蔦慶，陳敏，溫熙森．隨機共振理論在轉子碰摩故障早期檢測中的應用［J］．機械工程學報，2001，37（9）：88－91．HU Niao-qing，CHEN Min，WEN Xi-sen．Application of stochastic resonance theory for early detection rub-impact fault of rotor system ［J］．Journal of Mechanical Engineering，2001，37（9）：88－91．

［4］郝研，王太勇，萬劍，等．基于級聯雙穩隨機共振和多重分形的機械故障診斷方法研究［J］．振動與沖擊，2012，31（8）：181－185．HAO Yan，WANG Tai-yong，WAN Jian，et al．Mechanical fault diagnosis based on cascaded biatable stochastic resonance and multi-fractal［J］．Journal of Vibration and Shock，2012，31（8）：181－185．

［5］Shneidman V A，Jung P，Hanggi P．Weak-noise limit of stochastic resonance［J］．Physical Review Letters，1994，72（17）：2682－2685．

［6］韓東穎，丁雪娟，時培明．基于自適應變尺度頻移帶通隨機共振降噪的EMD多頻微弱信號檢測［J］．機械工程學報，2013，49（8）：10－18．HAN Dong-ying， DING Xue-juan，SHI Pei-ming． Multifrequency weak signal detection based on EMD after denoising by adaptive re-scaling frequency-shifted band-pass stochastic resonance ［J］． Journal of Mechanical Engineering，2013，49（8）：10－18．

［7］Fox R F．Stochastic resonance in a double well［J］．Physical Review A，1989，39（8）：4148－4153．

［8］Gandhimathi V M，Murali K，Rajasekar S．Stochastic resonance in overdamped two coupled an harmonic oscillators［J］．Physica A，2005，347：99－116．

［9］Rana S，Lahiri S，Jayannavar A M．The role of soft versus hard bistable systems on stochastic resonance using average cycle energy as a quantifier［J］．The European Physical Journal B，2011，84：323－329．

［10］林敏，黃詠梅，方利民．耦合雙穩系統的隨機共振控制［J］．物理學報，2008，57（4）：2048－2052．LIN Min，HUANG yong-mei，FANG Li-min．The stochastic resonance control of coupled bisatable systems［J］．Acta Physica Sinica，2008，57（4）：2048－2052．

［11］Gandhimathi V M， Murali K， Rajaekar S． Stochastic resonance in overdamped two coupled anharmonic oscillators［J］．Physica A，2005，347（1）：99－116．

［12］Dykman M I，Haken H，Hu G．Linear response theory in stochastic resonance［J］．Physical Letters A，1993，180（4－5）：332－336．

［13］林敏，方利民，朱若谷．雙頻信號作用下的耦合雙穩系統的雙共振特性［J］．物理學報，2008，57（5）：2648－2643．LIN Min，FANG Li-min，ZHU Ruo-gu．The dual-resoannce characteristic of coupled bistable system affected by twofrequency signal［J］．Acta physica sinica，2008，57（5）：2648－2643．

［14］ Gammaitoni L，Marchesoni F，Menichella S E，et al．Stochastic resonance in bistable systems［J］． Physical Review Letters，1989，62（4）：349－352．

［15］冷永剛，王太勇．二次采樣用于隨機共振從強噪聲中提取弱信號的數值研究［J］．物理學報，2003，52（10）：2432－2437．LENG yong-gang，WANG tai-yong．Numerical research of twice sampling stochastic resonance for the detection of a weak signal submerged in a heavy noise［J］．Acta Physica Sinica，2003，52（10）：2432－2437．