一種特殊的布拉格型聲子晶體桿振動帶隙研究

舒海生，張 法，劉少剛，高恩武，李世丹，董立強

（哈爾濱工程大學 機電工程學院702所，哈爾濱 150001）

周期結構被廣泛地應用在工程結構中，與之相關的減振降噪研究受到了眾多研究者的關注。在對周期結構振動研究中發現，其特有的“天然”振動帶隙特性為振動隔離提供了一種新思路。類似地，近年來提出的聲子晶體本質上也是一種周期結構，一般是指彈性常數及密度周期分布的材料［1］，對聲子晶體的研究主要集中在帶隙形成機理和計算方法等領域，研究對象主要為桿、板、殼以及旋轉類結構等［2－7］，這些研究對象相對簡單，對于工程中常見的組合式結構研究較少［8－9］。建筑和橋梁工程中常見鋼結構往往是通過組合式的桿或梁來承載的，其基本單元一般可簡化為雙聯角桿或三聯T型桿；機械結構中也常常采用組合桿，例如T型助力機械手，此外醫用救護車擔架的支架、汽車保險杠、飛機尾翼中也常常見到組合桿結構。振動在該類結構中的傳播特性與單桿顯然是不同的。在我們前期對基于聲子晶體思想的雙聯角桿與T型桿的振動特性的研究基礎上［10－11］，本文進一步針對布拉格型聲子晶體T形桿，將不同彈性常數的兩種材料周期交替地連接在一起，通過傳遞矩陣法構造波傳播模型，推導了有限周期T形桿的振動傳遞函數；同時利用有限元法仿真分析了振動傳輸特性，并對理論和仿真結果進行了對比，面內和面外振動分析結果表明，聲子晶體T形桿對振動波的衰減能力優于單一材料桿，具有明顯的多維寬頻減振特性，從而為工程中的組合桿支撐結構的減振問題提供了一種新的設計思路。

1 布拉格型聲子晶體T形桿

如圖1（a）所示為布拉格型T形桿示意圖，材料A、B周期交替聯接，該組合桿可視為由三根單桿通過連接塊組合而成，將三桿編號為a、b、c，并在其起始端分別構建坐標系。a＝a1＋a2為晶格常數，a1、a2分別表示兩種材料的長度；周期數為n。桿的橫截面為矩形，長寬分別設為b、h。

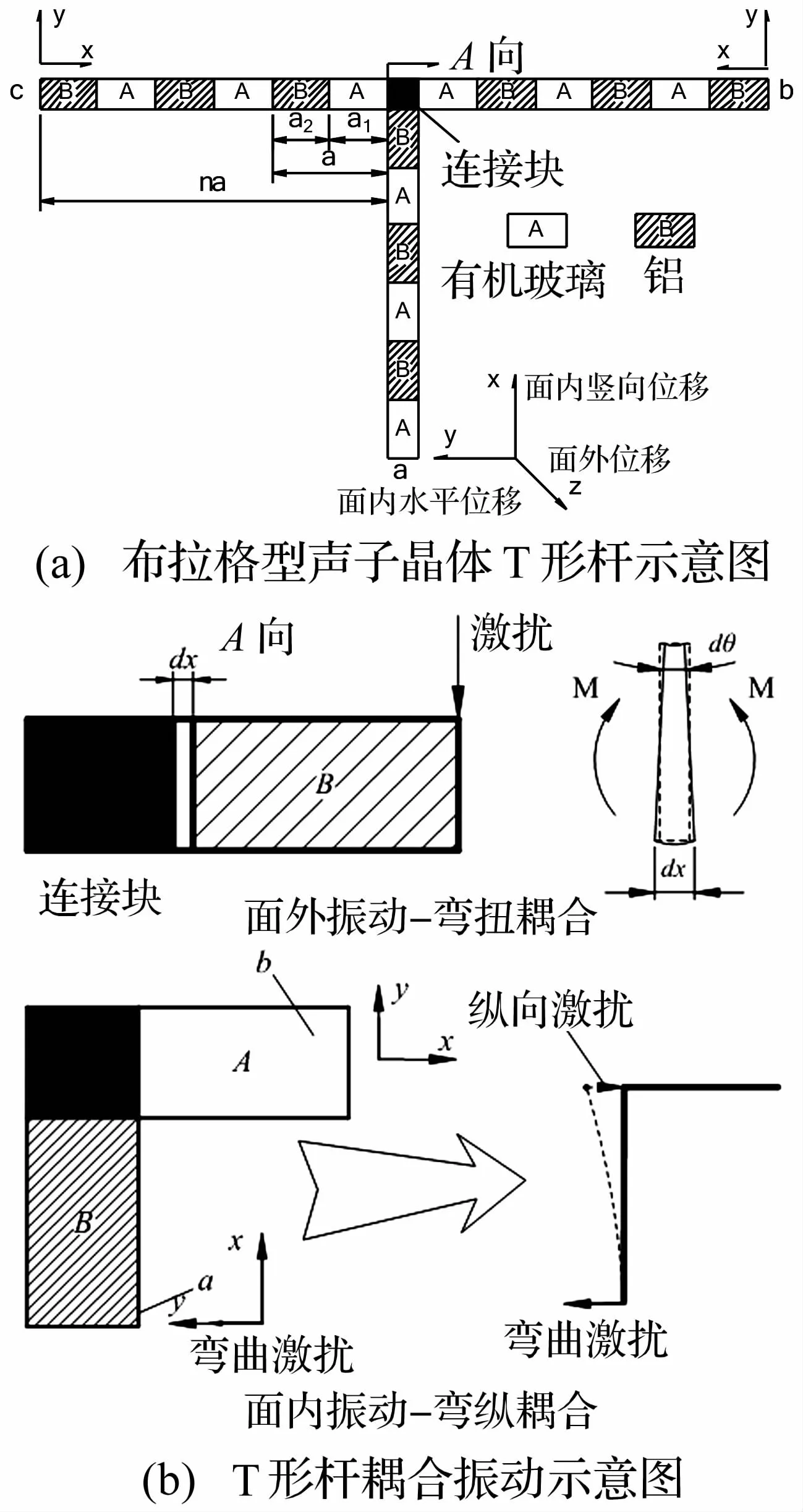
圖1 布拉格型聲子晶體T形桿振動分析Fig．1 PCT vibration analysis

如圖1（b）所示，當在T形桿a端施加垂直紙面的彎曲振動激擾時，振動波會沿a桿通過連接塊傳遞到b和c桿，當其通過連接塊時彎曲波會發生彎扭耦合效應。如圖中A向所示，當垂直于紙面的彎曲振動傳播到連接塊與材料B接觸的截面時，會對連接塊截面微元產生彎矩，使截面產生微小形變，這種形變會對b桿產生一定的扭轉角，a桿上傳遞彎曲形變對b桿起始端產生了扭轉變形，a桿所受彎矩轉變為b桿的扭矩。

2 T形桿面外振動分析

在a端施加z向的振動激勵，則面外彎曲波沿桿方向傳播，在三桿的結合處由彈性波的連續傳播性可以得到2個條件：桿a末端位移＝桿b始端位移、桿a末端剪力＝桿b始端剪力；同時根據這種耦合傳播效應，在連接處會得到以下4個協調條件：桿a末端轉角＝桿b始端扭轉角、桿a末端的扭轉角＝桿b始端轉角、桿a末端彎矩＝桿b始端扭矩、由于T形桿的對稱性桿a末端的扭矩＝2倍的桿b始端彎矩，上述協調關系可用矩陣形式表為：

式中：

其中腳標第一個字母表示周期數，第二個字母表示材料種類1表示材料A，2表示材料B，上標表示桿。E為楊氏模量，G為剪切模量，I為截面慣性矩，Ip為截面極慣性矩，α＝ω／c，c為扭轉振動波在某種介質中的傳播速度 c2＝G／ρ，λ4＝ρAω2／EI，A為截面面積，ω為角頻率，j為虛數單位。其中：

同理，當彎曲波在桿中傳播到第n周期材料A與材料 B交界面時，x＝（n－1）a＋a1，即 x′＝a1，由結合處的連續性可得位移、轉角、彎矩、剪力、扭角及扭矩的

傳遞矩陣：

式中各參數含義同上，其中：

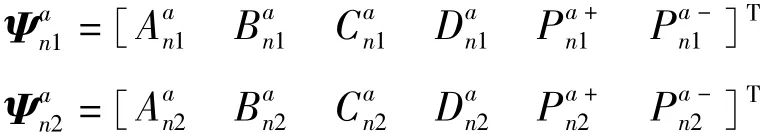
同理，在第n－1周期與第n周期交界面，即在x＝（n－1）a處，對于第n－1周期的材料B來說，x′＝a，對于第n周期的材料A來說x′＝0，類似地，傳遞矩陣可表為：

其中：

由式（2）、（3）可得彎曲波第n周期和第n－1周期之間的傳遞關系：

式中 T′＝（K2）－1H2（H1）－1K1為單桿傳遞矩陣。

由式（1）、（2）及式（4）可得：

式中T形桿的總傳遞矩陣為：

T＝（H1）－1K1（T′）n－1（K0）－1H0（H1）－1K1（T′）n－1，其中n為T形桿周期數。

當在a桿的下端加載振幅為u0的寬頻激勵，b桿末端為自由時，其邊界條件可寫為：a桿始端位移＝μ0、a桿始端轉角＝0、a桿始端扭轉角＝0、b桿末端彎矩＝0、b桿末端剪力＝0、b桿末端扭矩＝0。以矩陣形式可表為式（6）、（7）：

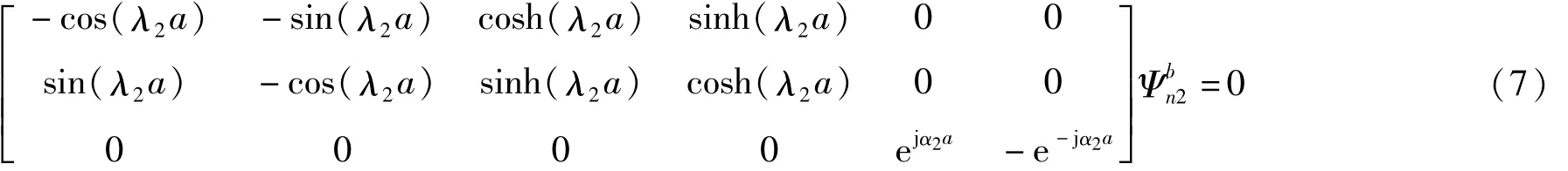
將式（5）代入到式（7），并將所得矩陣與式（6）合并，可得：

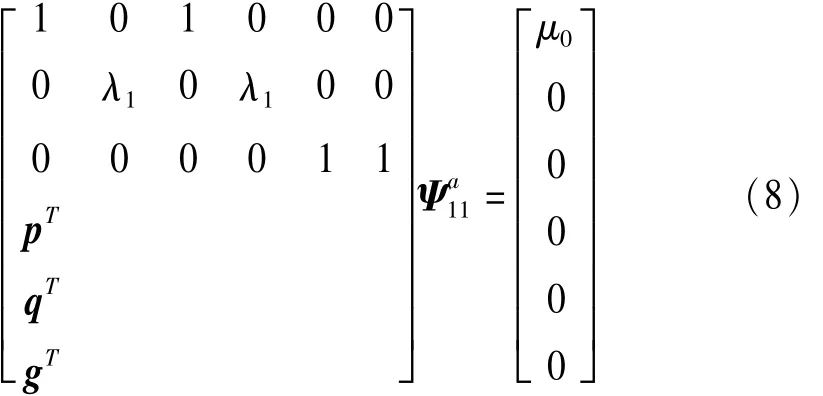
式中：

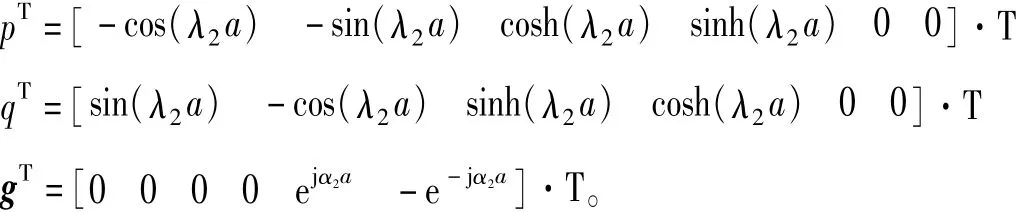
b桿的末端振動幅值可表示為：

將式（5）代入上式，可得：

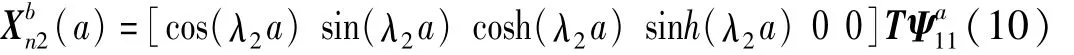
以分貝表示的振動衰減量即可寫為：

根據以上推導過程，分別在MATLAB和ANSYS環境下進行了數值分析和仿真計算，其中材料A設定為有機玻璃，材料B設為鋁，其它參數參見表1。

在a端施加垂直T型桿平面的彎曲振動激勵，其傳輸特性如圖2所示，其中（a）為數值計算所得頻響函數曲線圖，（b）為仿真計算所得頻響函數曲線，實線和虛線分別表示聲子晶體T形桿和單一材料T形桿對面外彎曲振動的衰減值，點劃線表示輸入激擾。從圖（b）中可以看出，實線所表示的布拉格型聲子晶體T形桿對于輸入激擾振動的衰減性能明顯優于單一材料構成的T形桿。

對比（a）和（b）兩圖可以發現數值計算結果與仿真計算結果基本吻合，在0～8 000 Hz范圍內出現了多個振動帶隙，其中存在兩個較大的振動帶隙即衰減區域，第一個帶隙的起止頻率為1 520～3 260 Hz，最大衰減值達60 dB；第二個帶隙的起止頻率為4 580～6 780 Hz，最大衰減值達44 dB，帶隙最大跨度可達2 200 Hz。同時在0～1 500 Hz范圍內出現三個較窄的衰減區域，平均衰減值為20 dB左右，因此T形桿對于中低頻段的振動也具有一定的減振性能。

表1 T形桿材料和結構參數Tab．1 The Material and Structural parameters of T－type rod

圖2 布拉格型T形桿面外振動頻率響應函數曲線Fig．2 The Bragg T rod frequency response function of out-of-plane vibration

圖3 布拉格型T形桿豎直振動頻率響應函數曲線Fig．3 The Bragg T rod frequency response function of vertical vibration

圖4 布拉格型T形端水平振動頻率響應函數曲線Fig．4 The Bragg T rod frequency response function of horizontal vibration

3 T形桿面內振動分析

類似的，如圖1（b）所示，當a桿下端受到沿y軸面內彎曲振動激擾時，振動會沿a桿通過連接塊傳遞到b、c桿上，當傳播至結合處（圖中黑色處）時會發生彎縱耦合效應。假設將連接塊看作為一個集中質量點，當振動波傳播至該點時，會使其產生一個沿b桿軸線方向的振動，波型發生轉化，從而使b桿發生縱振，進而導致彎縱耦合，a桿所受剪力轉變為b桿所受縱向力；同理，當a桿下端受到沿軸線方向的面內振動（縱振）時，通過連接塊a桿的縱振會使b桿作彎曲振動，此時a桿所受縱向力轉變為b桿所受剪力。

對于T形桿面內振動的數值推導部分，由于縱振與扭振的波動方程解相似，只需對某些參數進行替換即可，因而此處的推導不再贅述。

需要指出的是，由于面內任意方向的激擾均可分解為沿x與y軸（即豎直和水平）方向，因此本文將分別對沿a端坐標方向施加位移激擾進行計算，振幅均設為 u0。

圖3給出了對a端施加面內豎直方向振動激勵時，T形桿的頻響函數曲線，其中（b）為仿真計算所得頻響結果，實線和虛線分別表示聲子晶體T形桿和單一材料T形桿對面外彎曲振動的衰減值，點劃線表示輸入激擾。對比（a）、（b）兩圖可知，數值計算結果與仿真計算結果基本吻合，存在多個振動衰減區域，尤其是在4 280～8 000 Hz頻率范圍內除少許共振峰外，其余頻率范圍均處在衰減區域，平均衰減值可達20 dB以上。

圖4給出了對a端施加面內水平方向振動激勵時，T形桿的頻響函數曲線。可以發現圖中存在兩個較大帶隙，起止頻率分別為1 540～3 310 Hz和4 620～6 660 Hz，其最大衰減值可達50 dB。從仿真結果上可以看出，聲子晶體T形桿對共振峰值也有良好的抑制效果。

4 結 論

針對布拉格型聲子晶體T形桿進行了振動特性研究，分別采用傳遞矩陣法和有限元仿真進行了數值和仿真分析，分析結果表明：

（1）通過對比布拉格型聲子晶體T形桿和單一材料的T形桿的振動傳輸特性曲線，可知聲子晶體T形桿對空間任意方向振動激擾的減振能力均明顯優于單一材料桿，因而更適合于工程中的多維減振需求；

（2）該聲子晶體T形桿能夠實現振動波型的轉化，在一種振動的傳遞率等式中均包含著兩種波的傳遞矩陣，這種振動波形的轉化使其產生了帶隙疊加的效果，從而有利于桿件對不同類型振動激擾的抑制；

（3）不同方向振動激擾的頻響函數結果表明布拉格型聲子晶體T形桿具有多維寬頻減振的能力，但這種寬頻的減振帶隙多出現于中高頻范圍，為此可以進一步引入壓電材料加以主動調節，從而使得該帶隙向低頻移動，這也是我們的下一步工作重點。

［1］溫熙森，溫激鴻，郁殿龍，等．聲子晶體［M］．北京：國防工業出版社，2009．

［2］Diaz-de-Anda A．，Pimentel A，Flores J． et al． Locally periodic Timoshenko rod：experiment and theory［J］．Journal of the Acoustical Society of America，2005，117（5）：2814－2819．

［3］Alakebanga T N T．Finite element and experimental analysis of wave propagation in conical periodic structures［D］．Washington DC：The Catholic University of America，2003．

［4］Toso M．Wave propagation in rods shell and rotating shafts with non-uniform geometry［D］．Washington DC：University of Maryland，2004．

［5］Jeong S M．Analysis of vibration of 2－D periodic cellular structures［D］．Atlanta：Georgia Institute of Technology，2005．

［6］Chen Sheng-bing，Wen Ji-hong，Yu Dian-long，et al．Band gap control of phononic beam with negative capacitance piezoelectric shunt［J］．Chin．Phys．B．2011，20（1）：14301．

［7］Martinsson PG，Movchan A B．Vibrations of lattice structures and phononic band gaps［J］．Q．J．Mech．Appl．Math．，2003，56：45－64．

［8］沈惠杰，郁殿龍，溫激鴻，等．平面周期管系對軸向波與彎曲波的隔離特性［J］．振動與沖擊，2011，30（3）：42－46．SHEN Hui-jie，YU Dian-long，WEN Ji-hong，et al．Transfer properties of longitudinal vibration wave and flexural vibration wave in Bragg periodic L-shaped pipe［J］．Journal of vibration and shock，2011，30（3）：42－46．

［9］Asiri S，Baz A，Pines D．Active periodic struts for a gearbox support system［J］．Smart Materials and Structures，2006（15）：1707－1714．

［10］ Shu Hai-sheng，Li Shi-dan，Dong Li-qiang，et al．A sonic crystal angular rod with ability of multi-dimensional and broadband vibration reduction［J］．Noise Control Engineering Journal，2013，60（1）：2042－2056．

［11］Shu Hai-sheng，Liu Shao-gang，Zhao Dan，et al．A combined sonic crystal rod of Bragg type with ability of vibration reduction in broad frequency band［J］．Noise Control Engineering Journal，2012，60（1）：42－61．