一種無需模型參數的無線傳感器網絡定位算法*

張 鵬 馮 欣 周建國 鄒進貴

1)武漢大學測繪學院，武漢 430079

2)精密工程與工業測量國家測繪地理信息局重點實驗室，武漢 430079

一種無需模型參數的無線傳感器網絡定位算法*

張 鵬1，2)馮 欣1)周建國1)鄒進貴1，2)

1)武漢大學測繪學院，武漢 430079

2)精密工程與工業測量國家測繪地理信息局重點實驗室，武漢 430079

提出一種無需模型參數的RSSI定位算法(二重消元法)。該算法通過對傳播模型的處理，消去模型參數，并結合截斷奇異值分解法求解方程組，實現節點實時定位，減少了傳統RSSI定位技術的測試開銷。仿真結果顯示，二重消元法在一定程度上可以提高定位精度，適用于模型參數未知或不斷變化的應用場景。

無線傳感器網絡;節點定位;RSSI;二重消元法;TSVD

無線傳感器網絡(wireless sensor network，WSN)是由具有感知能力、通信能力、計算能力的傳感器節點以無線形式構成的自組織網絡［1］，而節點定位技術作為目標監測與跟蹤等眾多應用的基礎，已成為近年來位置感知領域的研究熱點。目前，無線傳感器網絡大多采用基于接收信號強度指示(received signal strength indication，RSSI)的測距定位技術，其定位性能與信號傳播模型密切相關。文獻［2－3］提出的曲線擬合建模和多元線性回歸建模法，均依賴于定位前實驗現場的采樣數據，不適于臨時部署、快速定位或無法離線建模的場景，如毒氣檢測、火場救援等。另外，在復雜環境中，通過少量采樣數據獲取的模型參數不一定準確。文獻［4］提出一種無線信號傳播模型線性化法，實現了不依賴模型參數的目標定位，但定位精度較差。文獻［5－6］通過參考節點間的距離和信號強度實地計算模型參數，但不適于參考節點無法通信的網絡。針對上述問題，本文提出一種無線信號模型消元法(簡稱二重消元法)。通過對信號模型的處理，結合截斷奇異值分解法(truncated singular value decomposition，TSVD)計算節點坐標，不依賴于具體環境的模型參數。仿真結果表明，二重消元法能在一定程度上提高定位精度。

1 RSSI測距模型

基于RSSI的測距技術是通過測量信號從發射端到接收端的衰減來計算節點間的實際距離［7］。本文采用 Shadowing理論模型［8］:

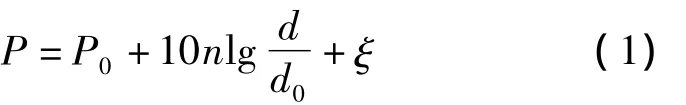
式中，d0為近地參考距離，P0是距離為d0時的接收信號強度，d為距發射端的真實距離，P是距離為d時的接收信號強度。ξ為遮蔽因子，n是路徑損耗指數，其數值取決于無線信號的傳播環境。由于在實際環境中ξ是均值為0、標準差為σ的正態隨機變量，為了簡化，將ξ的影響忽略，選用以下模型:

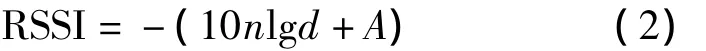
其中，參數A被定義為用dBm表示的距離發射節點1 m處的平均接收信號強度，RSSI為距發射節點d處的接收信號強度。模型參數A、n直接影響到RSSI測距精度，因此在模型參數無法獲取或取值不準確的情況下，RSSI定位算法的定位精度可能受到很大影響。

2 二重消元法

2.1 二重消元法原理

通常情況下，基于RSSI測距的定位算法需獲取距離信息后才能實現定位，而模型參數的取值是利用信號模型計算距離的關鍵因素，因此這類算法無法適用于模型參數未知的特殊場合。此外，由于定位環境中存在大量的反射、散射、繞射現象，通過事先采樣建立的信號傳播模型并不一定準確。這樣不僅增加測試開銷，獲取的精度也不高。二重消元法在一定程度上解決了這些問題。

圖1 節點分布圖Fig.1 Distribution of nodes

如圖1所示，設定位場景中有N個參考節點(N≥4)，位置坐標依次為(x1，y1)，(x2，y2)，(x3，y3)，…，(xN，yN)，未知節點個數為M，P為其中的一個未知節點，坐標為(x，y)。P到各參考節點的RSSI依次為(R1，R2，…，RN)，相應地到各參考節點的距離依次為(d1，d2，…，dN)。當采用簡化的測距模型時，對于每個未知節點(如P)，有如下方程式:

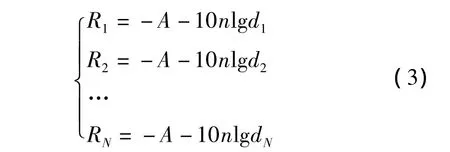
將式(3)中的第一式分別與其后的方程式相減，即可消除參數A:

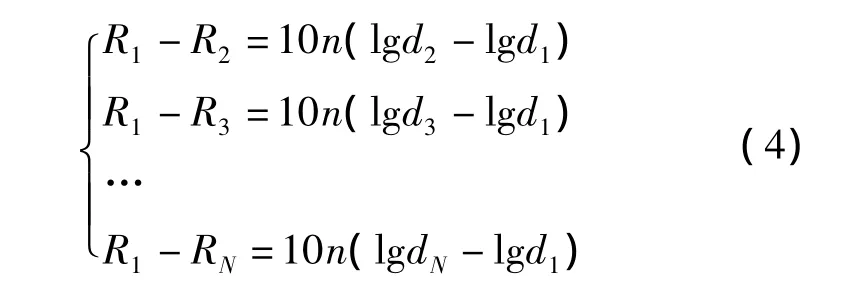
將處理后的方程組中的第一式再與其后的方程式相除，即可消除參數n:

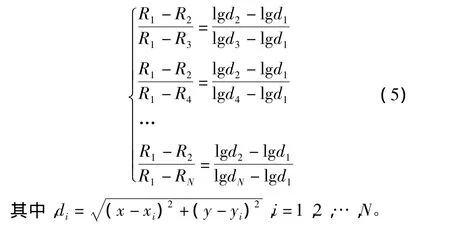
求解非線性方程組(5)，未知參數為待定位節點的坐標(x，y)。將式(5)中的方程式轉換后，選用泰勒級數展開迭代法進行求解，并忽略高階項，(x0，y0)是未知節點P的初始坐標。

令(x0，y0)=(x0+ Δx，y0+ Δy)，代入原方程式繼續求解。反復迭代，直到Δx、Δy滿足預先設定的門限ε為止，此時(x0，y0)即是未知節點的最終估計坐標。其中，節點的初始坐標可采用加權質心法獲取。為了防止迭代收斂過慢損耗節點能源，在程序中設定了迭代次數的上限(實驗中設為50次)。

2.2 TSVD求解方程

由于RSSI數據易受環境因素的干擾，為了避免測量誤差在矩陣求逆過程中放大，影響定位精度，本文利用截斷奇異值分解法(TSVD)［9］求解未知向量X，以解決方程解算中的病態問題。過程如下:

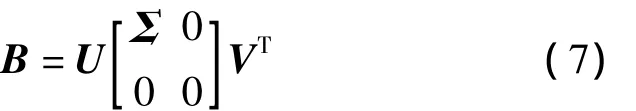
假設矩陣Bm×n(m≥n)的秩為r，那么其奇異值滿足σ1≥…≥σr＞σr+1=…=σn=0。變量Σ是一個降階的含有非負元素的對角矩陣，與矩陣B具有相同的維數，即 Σ =diag(σ1，…，σr)。矩陣 U、V 是正交矩陣，U=［u1，…，um］∈Rm×m，V=［v1，…，vm］=(vik)∈Rn×n，則矩陣B的廣義逆、向量X的廣義逆解如下:

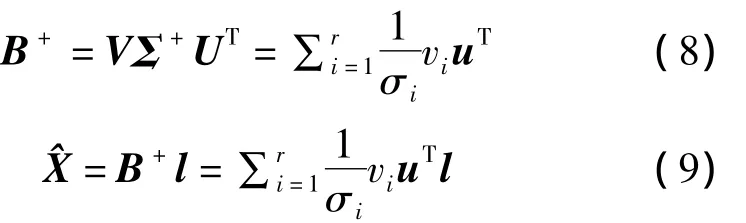
當奇異值σi異常小時，解的計算不穩定并且方差很大，從而導致估算值與準確值相差甚遠。TSVD通過舍棄較小的奇異值，有效地解決矩陣求逆中計算結果不準確或發散的情況，更好地表達矩陣的本質信息，抑制噪聲的影響。設q為應截斷的奇異值個數，此時 Σr－q=diag(σ1，…，σr－q)，則截斷奇異值分解得到的參數解為:

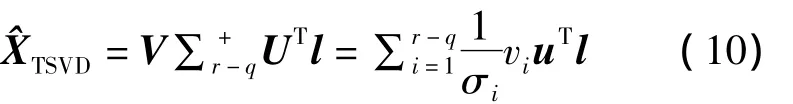
選取截斷參數q的方法［5］是:設定參數κ，κ為前r－q個奇異值之和與r個奇異值總和的比值，當κ約等于某一具體數值時，所對應的q即為截斷參數的取值。κ的具體數值將在實驗部分討論。

3 仿真及分析

本文用MATLAB對二重消元法進行仿真分析，并與相關算法進行比較。仿真區域設置為50 m×50 m，錨節點數目為5，指定分布在定位場景內。未知節點數目為100，均勻分布，如圖2所示。由于二重消元法無需模型參數，即參數的選取對定位結果影響不大，因此測試數據中設定A=－30，路徑損耗指數n=3，以便實驗仿真。以下所有仿真實驗均運行10 000次，取平均值作為最后結果。

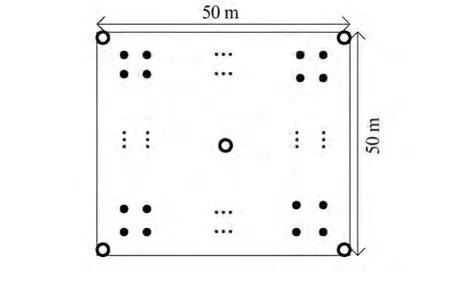
圖2 定位場景圖Fig.2 Site of locating

3.1 參數κ的取值

首先要探討二重消元法中TSVD解算階段的參數κ，其取值與截斷參數q及向量X的最終結果密切相關。表1、表2分別顯示了κ取不同數值時的定位精度及定位率。從定位精度的角度來看，當環境噪聲較小時，奇異值矩陣中的不可靠成分較少，κ取值越大，保留的可靠成分越多，定位精度越高;當環境噪聲較大時，矩陣中不可靠成分較多，κ取值相對越小，截掉的不確定成分越多，定位精度相應越高;當環境噪聲不大不小時，κ取值較小可能會刪除可靠成分，κ取值較大可能仍保留較多的不可靠成分，此時κ取值適中的定位結果最好。從定位率的角度來看，κ取值越小，定位率越高。結合定位環境特性，同時從表1中可看出，當κ≥0.80時，定位精度相差不大;從表2中看出，當κ=0.80時，隨噪聲變化的定位率等于或接近于100%。因此，二重消元法中選取κ=0.80，來實現定位精度和定位率的折中。

3.2 算法比較

針對不同的環境噪聲，比較二重消元法(κ=0.80)、文獻［4］中的線性化法及最大似然法，其中最大似然法使用的模型參數跟設定參數大小相同，即在仿真中最大似然法只受到環境噪聲的影響，達到最大似然定位的最佳情況。此外，κ=0.80時，定位率在環境噪聲較大時只是接近于100%，見表2。在計算平均定位誤差時，對于二重消元法中計算發散的點，另兩種算法不將其計入平均定位誤差內。

從圖3可知，當環境噪聲較小，如σ=1時，最大似然法和二重消元法的定位精度相近，遠優于線性化法。隨著環境噪聲的增大，3種定位算法的定位誤差都不斷增大，但二重消元法的增長幅度明顯小于最大似然法，線性化法的增長幅度最小，但該算法的定位精度很差。因此，利用二重消元法進行節點定位可以在降低測試開銷的情況下有效地提高定位精度。但在環境噪聲很大時，二重消元法可能會有少量的節點無法定位。如何提高這種場景下算法的收斂性是今后要研究的重點內容。

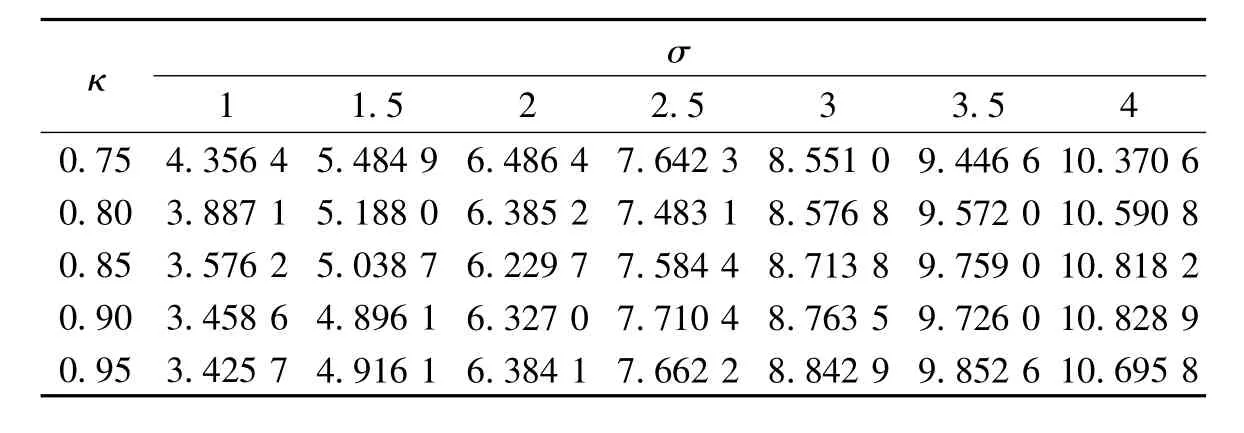
表1 不同κ、σ下的定位精度Tab.1 Locating accuracy under different κ、σ

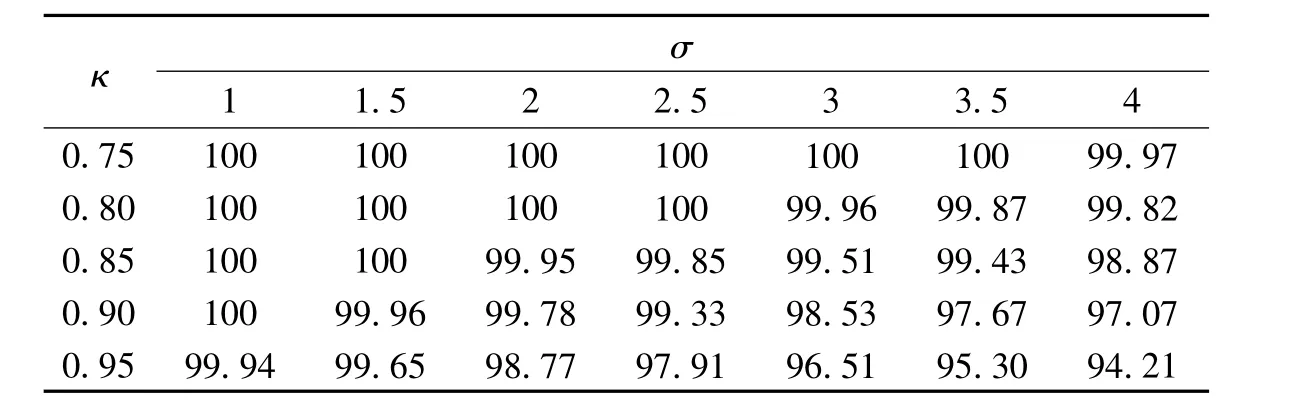
表2 不同κ、σ下的定位率(單位:%)Tab.2 Locating rate under different κ、σ

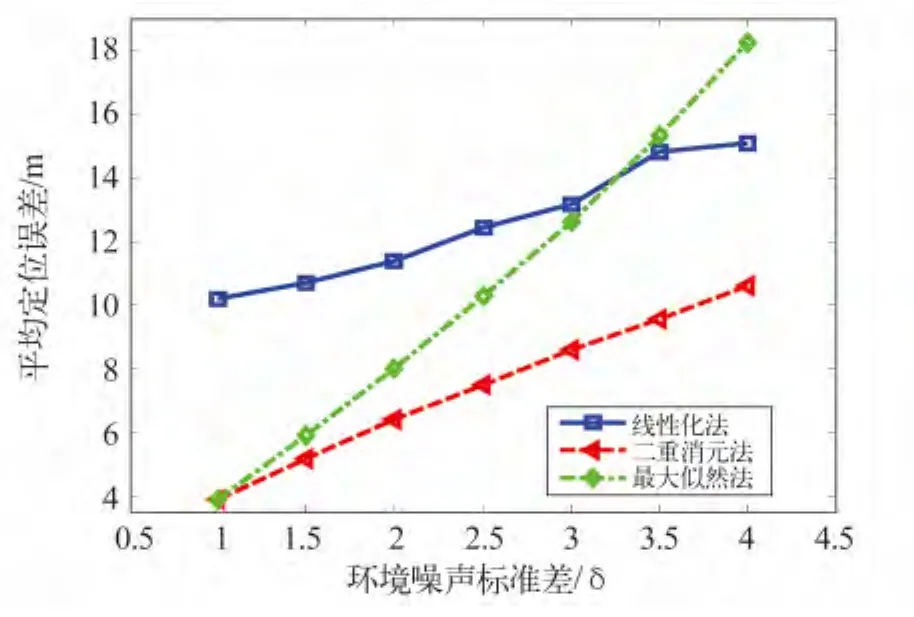
圖3 3種算法的定位精度比較Fig.3 Accuracy comparison of three kinds of algorithms

在二重消元法定位率為100%時，進一步分析3種算法的平均定位誤差累積分布。這里選取環境噪聲不大不小的情況(σ=2.5)來討論。

圖4、圖5分別描述了σ=2.5時3種算法的平均定位誤差累積分布及每個未知節點的誤差大小。從圖中看出，二重消元法定位誤差較小的節點比例明顯要多，相較于另外兩種算法而言，大部分節點總是取得最優的定位結果。對于一些無需精確坐標的位置服務場景，二重消元法能較好地實現定位。

4 結語

本文針對基于RSSI的無線傳感器網絡定位中建模參數的問題，提出了二重消元法。該算法對信號傳播模型進行消元處理，結合TSVD理論，能夠使用實時測量的RSSI值動態地估計節點位置。從仿真結果可知，二重消元法不但可以避免事先建模所需的測試開銷，還可以在一定程度上提高定位精度，在無法獲取模型參數或不斷變化的特殊場合具有很大的優勢。由于在噪聲很大的場景中該算法的定位率并沒有達到100%，下一步希望在算法模型的解算階段結合正則化理論，來提高算法的魯棒性和收斂性。

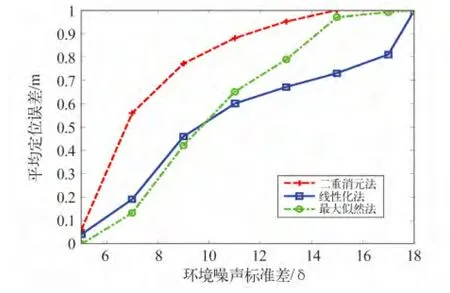
圖4 平均定位誤差累積分布(σ=2.5)Fig.4 Distribution of cumulated mean locating error

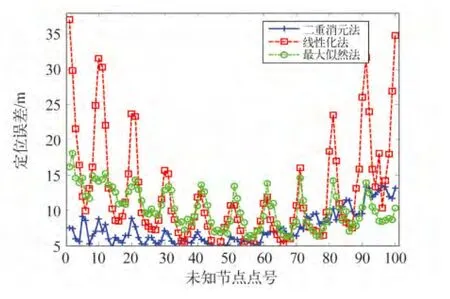
圖5 未知節點定位誤差比較Fig.5 Comparison of locating error for unknown nodes

1 孫立民，李健中，陳渝，等.無線傳感器網絡［M］.北京:清華大學出版社，2005.(Sun Limin，Li Jianzhong，Chen Yu，et al.Wireless sensor network［M］.Beijing:Tsinghua University Press，2005)

2 方震，趙湛，郭鵬，等.基于RSSI測距分析［J］.傳感技術學報，2007(11):2 526 － 2 530.(Fang Zhen，Zhao Zhan，Guo Peng，et al.Analysis of distance measurement based on RSSI［J］.Chinese Journal of Sensors and Actuators，2007(11):2 526－2 530)

3 袁正午，鄧思兵，李恭偉.基于多元線性回歸快速迭代的室內定位方法研究［J］.計算機應用研究，2007(12):121－122.(Yuan Zhengwu，Deng Sibing，Li Gongwei.New indoor positioning method based on multiple linear regression iteration［J］.Application Research of Computers，2007(12):121－122)

4 Koo J，Cha H，Localizing WiFi access points using signal strength［J］.Communications Letters IEEE，2011，15(2):187－189.

5 Lim H，Kung L C，Hou J C，et al.Zero-configuration，robust indoor localization:theory and experimentation［C］.IEEE Infocom’06，2006.

6 周建國，張鵬，馮欣.自適應無線傳感器網絡室內定位算法［J］.大地測量與地球動力學，2012，32(2):74 －77.(Zhou Jianguo，Zhang Peng，Feng Xin.Adaptive algorithm for wireless sensor network indoor positioning［J］.Journal of Geodesy and Geodynamics，2012，32(2):74 －77)

7 安德烈·戈德史密斯.無線通信［M］.北京:人民郵電出版社，2007.(Goldsmith A.Wireless communicatio［M］.Beijing:People Post Press，2007)

8 Patwari N，Ash J N，Kyperountas S.Locating the nodes:cooperative localization in wireless sensor networks［J］.Signal Processing Magazine IEEE，2005，22(4):54 －69.

9 Ke C，Qingming G.TSVD regularization in GPS multicorrelator multipath estimation［C］.Artificial Intelligence，Management Science and Electronic Commerce(AIMSEC)，2011.

NODE LOCATING IN WIRELESS SENSOR NETWORK WITHOUT A PRIOR KNOWLEDGE OF CHANNEL MODEL PARAMETERS

Zhang Peng1，2)，Feng Xin1)，Zhou Jianguo1)and Zou Jingui1，2)
1)School of Geodesy and Geomatics，Wuhan University，Wuhan 430079
2)The Key Lab of Precise Engineering and Industry Surveying，NASMG，Wuhan430079

A RSSI algorithm without a prior knowledge of channel model parameters for node locating in Wireless Sensor Network was proposed in the paper.It can be realized using the algorithm real-time location estimation by coping with the channel model and TSVD to solve the equation.Extensive simulation results show that locating accuracy using the algorithm is higher than some of other RSSI algorithms，and the algorithm is especially suitable to the cases of absence or incorrectness of the channel model parameters.

wireless sensor networks;node localization;RSSI;double-elimination algorithm;TSVD

P228

A

1671-5942(2014)05-0174-04

2013-05-04

國家自然科學基金項目(41074025);高等學校博士學科點專項科研基金項目(20110141120046)。

張鵬，講師，主要研究方向為無線傳感器網絡室內定位、壓縮感知理論和軟件接收機等。E－mail:pzhang@sgg.whu.edu.cn。